Received 10 April 2015; accepted 24 May 2015; published 27 May 2015

ABSTRACT

We consider an incompressible fluid in a rectangular nanochannel. We solve numerically the three dimensional Fourier heat equation to get the steady solution for the temperature. Then we set and solve the Langevin equation for the temperature. We have developed equations in order to determine relaxation time of the temperature fluctuations, τ_T = 4.62 × 10⁻¹⁰ s. We have performed a spectral analysis of the thermal fluctuations, with the result that temporal correlations are in the one-digit ps range, and the thermal noise excites the thermal modes in the two-digit GHz range. Also we observe long-range spatial correlation up to more than half the size of the cell, 600 nm; the wave number, q, is in the 10⁶ m⁻¹ range. We have also determined two thermal relaxation lengths in the z direction: l₁ = 1.18 nm and l₂ = 9.86 nm.

Keywords:

Nanochannels, Temperature Fluctuations, Random Heat Flow, Thermal Relaxation, Temporal and Spatial Correlations

1. Introduction

In recent years, with the advance of nanotechnology, there is interest in the fabrication of nano-scale devices powered by [1] or constructed using [2] so-called “Brownian motors”. W. Reisner et al. studied the physics and biological applications of DNA confinement in nanochannels [3] . Xu Hou et al. made a critical review of the biomimetic smart nanopores and nanochannels [4] . A. Lappala et al. performed a study of the ratcheted diffusion transport through crowded nanochannels [5] . Li-Jing Cheng presented a doctor of philosophy dissertation on ion and molecule transport in nanochannels [6] . Also, a series of pressure-sensitive microfluidic gates to regulate liquid flow have been successfully fabricated [7] . Yang and Kwok studied the microfluid flow with hydrophobic channel walls with electrokinetic effects and Naviers slip condition [8] . Also optical detection of single molecule in solution, inside submicrometer channels has become more and more important [9] -[11] . A fundamental understanding of the transport phenomena (fluid and energy) in nanofluidic channels is critical for systematic design and precise control of such miniaturized devices towards the integration and automation of Lab-on-a-chip devices. T.-C. Kuo et al. [12] investigated molecular transport through nanoporous nuclear-track- etched membranes with fluorescent probes by manipulating applied electrical field polarity, pore size, membrane surface functionality, pH, and the ionic strength. Y. Liu et al. [13] studied ion size and image effect on electrokinetic flows with the results that ion size had significant effects on electrokinetic flows in nanosystems. Stepišnik and Callaghan [14] [15] applied the NMR modulated gradient spin-echo method (MGSE) [16] to measure the velocity correlation and the diffusion coefficient of fluid in microcapillary. F. Detcheverry and L. Bocquet developed an analytical description of the thermally induced fluid motion. They estimated several physical quantities under thermal fluctuations [17] .

We believe that the knowledge of temperature correlations and the relaxation of the fluctuations could be important for a better understanding of channel fluid phenomena and design.

In the present work, we consider an incompressible fluid at rest in a nanochannel, in which the transfer of energy takes place entirely by thermal conduction. In order to report the temperature fluctuations, we set and solve the Langevin equation for the temperature.

2. Thermal Conduction

The heat flow is related to the temperature gradient by the Fourier law. However, when fluctuations are present, there also appear spontaneous energy fluxes disconnected from this gradient. The “random” contributions to the dissipative heat flux will be designed by. Then, the fluctuating phenomenological law read [18] :

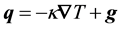(1)

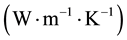
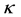is the thermal conductivity.

The equation of heat transfer is particularly simple for an incompressible fluid at rest, in which the transfer of energy takes place entirely by thermal conduction (see [18] [19] )

(2)

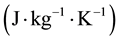
is the specific heat at constant pressure and 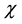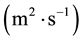is the thermometric diffusivity, defined as

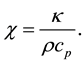(3)

The last term is the fluctuations contribution in accordance to Equation (1). We observe, in this case, the tem- perature equation is decoupled from the density and velocity equations.

2.1. Random Heat Flow

The correlations among the components of the random heat flow in an incompressible fluid are [18] :

(4)

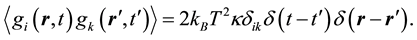(5)

Performing the derivative, we obtain:

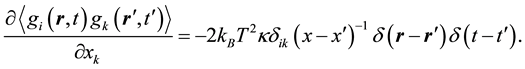(6)

In case we consider these magnitudes in the same volume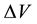, in an interval of time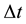, Equations (5) and (6) transform

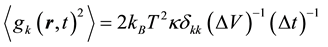(7)

(8)

Deriving inside the bracket, we obtain

(9)

Approximating inside the bracket of Equation (9), we obtain from Equations (7), (9)

(10)

Then we can write

(11)

If is the same for the three coordinates, we obtain,

(12)

or

(13)

with

(14)

where we have used, and is the thermal noise, defined by its statistical properties, namely,

(15)

(16)

i.e., the correlation time of the noise is zero.for this term. Then

(17)

We used the definition of the Wiener’s process (see [20] [21] ), where is the “Wiener’s increment”.

2.2. Langevin Equation for the Temperature

To numerically solve Equation (2) we need to perform a discretization. This is achieved by multiplying both members by and performing the integration in the interval, namely,

(18)

or

(19)

where in the last term of the former equation we have used Equation (17).

At the limit the mean values at the RHS of the former equation can be reemplace by the instantenous values, this means that the overline on the expressions can be omitted, while. From the developments in the appendix we need to recall here that the “Wiener’s process” is just a Gaussian stochastic process of width. Then, at each pass of the integration we have to draw and nor- malize the result properly. That is to say, if is an aleatory number, with Gaussian distribution, centered in and width 1. In MATLAB,; consequently we can write. To conclude the discretization process, Equation (19) is transformed in the corresponding Euler’s equation giving the temporal evolution of the temperature, namely,

(20)

Defining, we have

(21)

Then the temperature relaxation time, will be

(22)

From now on the averages are over the realizations of the stochastic process. A first basic quantity of interest is the average temperature current in the long-time limit (i.e, after transients due to initial conditions have died out)

(23)

where

(24)

where is the number of realizations.

2.3. Numerical Method

We consider a fluid in a rectangular cross section nanochannel, Figure 1, with the size along the x axis (width b) and the size along the y axis (height c). The length of the channel is denoted by L. The boundary conditions are:, ,. We have considered equal increments in the three coordinates, , consequently, we have to comply with the numerical stability condition, known as CFL (Courant-Friedrichs-Lewy), which reads for our case:

(25)

considering the equal sign, we obtain for the ratio of time to spatial increments

(26)

Then the discretization for the temperature equation envolving fluctuations, will be

(27)

The first step of the numerical procedure is the choice of the volume, and the corresponding spatial grid step, in our case. Next, the corresponding time step is evaluated from the CFL condition,

. In selecting the number of temporal steps the code needs to run, , we consider the temporal

interval of, enough for dying out of the transients due to initial conditions. Hence, , where. In our simulation, we have, then, , , and, , , , , , , , , the corresponding grid is points.

To numerically evaluate the steady state solution, , we proceed as follows: First we initialize our working grid by setting all the matrix components of the temperatures equal to zero,. Next, we solve simultaneously the Equations (27). Every 10 time steps we compute the difference between the actual tempera- tures and the temperature in the previous verification. The maximum of the differences

(28)

is referred to as the error. Time integration of the equations is stopped when the error is less than a tolerance defined at the beginning of the process. We have found that a tolerance tol = 10⁻⁹ gives reasonable results for the steady state solution. In this first part of our numerical procedure (namely, the evaluation of the steady state solution) we use deterministic equations, i.e. random noise is not considered.

After getting the steady state solution for the temperature,. Then we add the corresponding hydrodynamic fluctuation term to the temperature equation, solving this equation over temporal points and realizations of the stochastic process. Then we analyze the temporal and spatial correlations of the temperature, focusing our study in the center line temperature,.

In Figure 2, Figure 3 are shown two views of the steady solution.

3. Results

3.1. Thermal Relaxation

In Figure 4, is shown the temperature profile along y direction for versus the z axis distance to the wall,

is fitted with two exponential, the corresponding thermal relaxation lengths are and.

3.2. Autocorrelation Functions for the Central Line Temperature

We have performed spectral analysis of the fluctuations for the central line temperature. As an example of our results, we show in Figure 5(a) the temporal autocorrelation function for the mean (over stochastic realizations) central line (CL) temperature. We observe that the correlation function extends up to 10 ps. Correspondingly, in Figure 5(b), the Fourier transform of the former autocorrelation function (the spectral density of the mean CL temperature) goes up to the two-digit GHz band.

Regarding the spatial correlation we show in Figure 6(a) the normalized spatial (z axis) autocorrelation function for the mean CL temperature. We can observe that the correlation extends over more than half length of the cell, 600 nm, correspondingly, the Fourier transform of this function, Figure 6(b), extends up to wave numbers in the 10⁶ m⁻¹ range. As a validity test of the method we verify that the expectation value obeys the heat conduction equation. The deviations are less than 0.01%. Our present results demonstrate the generic spatially long-range character of nonequilibrium fluctuations.

4. Conclusion

These such long range correlations appear generically for a wide class of nonequilibrium states [22] . The predictions of this phenomenon have been made in a number of contexts, including self-organized criticality [23] , linear response [24] , nonequilibrium fluctuating hydrodynamics [25] , kinetic theory [26] , and stochastic hydrodynamic [27] - [30] .

Acknowledgements

We wish to thank the Fundación Santander-Central-Hispano (Programa de Visitantes Distinguidos UCM) for the support provided.

References

NOTES

^*On leave from Instituto de Física, Universidade Federal de Goiás, Goiás, GO, Brazil.