Journal of Biomaterials and Nanobiotechnology
Vol.06 No.02(2015), Article ID:54596,9 pages
10.4236/jbnb.2015.62008
Hydrodynamic Interactions Introduce Differences in the Behaviour of a Ratchet Dimer Brownian Motor
José A. Fornés*
Departamento de Fsica Aplicada I, Facultad de Ciencias Físicas, Universidad Complutense, Madrid, Spain
Email: jafornes@fis.ucm.es
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 February 2015; accepted 10 March 2015; published 12 March 2015
ABSTRACT
We use the Brownian dynamics with hydrodynamic interactions simulation in order to describe the movement of an elastically coupled dimer Brownian motor in a ratchet potential. The only external forces considered in our system were the load, the random thermal noise and an unbiased thermal fluctuation. We observe differences in the dynamic behaviour if hydrodynamic interactions are considered as compared with the case without them. In conclusion, hydrodynamic interactions influence substantially the dynamics of a ratchet dimer Brownian motor; consequently they have to be considered in any theory where the molecular motors are in a liquid medium.
Keywords:
Hydrodynamic Interactions, Motor Proteins, Molecular Dynamics, Brownian Dynamics, Fluctuation Phenomena, Random Processes, Noise, Brownian Motion

1. Introduction
Brownian motors are small physical micro- or even nano-machines that operate far from thermal equilibrium by extracting the energy from both thermal and non-equilibrium fluctuations in order to generate work against external loads. They present the physical analogue of bio-molecular motors that also work out of equilibrium to direct intracellular transport and to control motion in cells. In such bio-molecular motors, proteins such as kinesins, myosins and dyneins, move unidirectionally on one-dimensional “tracks” while hydrolysing adenosine triphosphate (ATP). These molecular motors are powered by a ratchet mechanism [1] ; they convert the nonequilibrium fluctuation into directed flow of Brownian particles in an asymmetrical periodic potential (ratchet) without any net external force or bias. Several authors have studied theoretically the transport of two coupled particles modeling the two heads of a motor protein [2] - [13] . Nonequilibrium fluctuations, whether generated or by a chemical reaction far from equilibrium, can bias the Brownian motion of a particle in an anisotropic medium without thermal gradients, a net force such as gravity, or a macroscopic electric field. Fluctuation-driven transport is one mechanism by which chemical energy can directly drive the motion of particles and macromolecules and may find application in a wide variety of fields, including particle separation and the design of molecular motors and pumps. Zimmermann and Seifert [14] studied the efficiencies of a molecular motor for a generic hybrid model applied to the F1-ATPase, and they obtained good quantitative agreement with the experimental data. Pinkoviezky and Gov [15] were motivated by the observed pulses of backward-moving myosin-X in the filopodia structure, and they modelled interacting molecular motors with an internal degree of freedom, introducing a novel modification to the approximation scheme.
In the present work, we use the Brownian dynamics with hydrodynamic interactions simulation in order to describe the movement of an elastically coupled dimer Brownian motor in a ratchet potential. In Section 2, we describe the forces acting on an oscillating dimer in a ratchet potential with a load force and an external unbiased fluctuation, which acts simultaneously on two particles. In Section 3, we describe the formalism given by Ermak and McCammon (1978) [16] , which couples the forces described in Section 2 and thermal noise with the diffusion tensor. A striking feature of fluid mechanics in the viscously dominated regime, or equivalently, at low Reynolds number, is the long range of hydrodynamic interactions. For example, the Stokeslet, or flow field induced by a point force, falls off inversely with distance. Hydrodynamic interactions have been considered by several authors to explain different phenomena. Kemps and Bhattacharjee, [17] , used a particle tracking model for colloid transport near planar surfaces covered with spherical asperities. This model provides a preliminary step in investigating how geometrically tractable asperities alter the undisturbed flow field and hydrodynamic interactions between the particle and the substrate. Hydrodynamic interactions allow in average for directed motion of a three-sphere system, and the spheres are connected by two identical active linker arms. Each linker arm contains molecular motors and elastic elements and can oscillate spontaneously; see [18] . Microorganisms are often subjected to swimming in close proximity to each other as well as other boundaries. The resulting hydrodynamic interactions may have puzzling effects on their swimming speed, trajectory, and power dissipation. These effects were investigated by Ramia et al. [19] ; each microorganism consisted of a sphere propelled by a rotating helix. It was found that only a small increase (less than 10%) resulted in the mean swimming speed of an organism swimming near and parallel to another identical organism. In a later paper, [20] focused on hydrodynamic interactions by considering two rotating rigid helices. They supposed that the helices were driven by stationary motors, and obtained complementary results to those of Ramia et al., since the hydrodynamic interactions between their helices were stronger. Recently Fornés, [21] , showed that hydrodynamic interactions induced movement against an external load in a ratchet dimer Brownian motor. In the present paper, we show that hydrodynamic interactions introduce differences in the behaviour of a ratchet dimer Brownian motor as compared without them. We report differences in the Peclet number, effective diffusion coefficient, mean 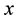 component of the mass center position and velocity and particles positions cross correlations in
component of the mass center position and velocity and particles positions cross correlations in 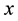 direction.
direction.
2. The Model
We consider an elastically coupled dimer in 3 dimensions in an asymmetrical potential (ratchet) in the 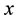 direction, see Figure 1. We considered a linear superposition of three spatial harmonics, following Ref. [22] ,
direction, see Figure 1. We considered a linear superposition of three spatial harmonics, following Ref. [22] ,
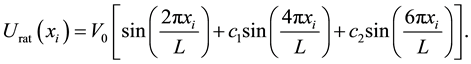 (1)
(1)
The corresponding force on the particles produced by the ratchet potential is given by:
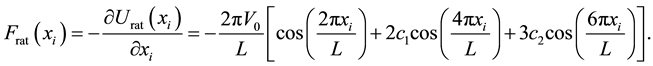 (2)
(2)
In the former equations 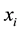 is the
is the 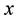 coordinate of particle
coordinate of particle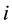 ,
, 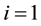 and 2, to distinguish the dimer particles. The parameters
and 2, to distinguish the dimer particles. The parameters 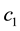 and
and 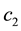 determine the ratchet profile. We use the parameters from Ref. [22] :
determine the ratchet profile. We use the parameters from Ref. [22] :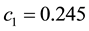 ,
, 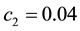 and
and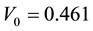 .
.
Figure 1. Dimer in an assymetrical ratchet potential under a constant load force, thermal noise and unbiased thermal sinusoidal fluctuation.
We define 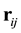 the vector from the center of particle
the vector from the center of particle 




i, j, k are unit vectors in the direction of the cartesian axis, with

Then the modulus of the harmonic force is,

where 

Then the components of the harmonic force are,

The corresponding components of the harmonic force on each dimer particle are,

Then the forces acting on the dimer particles are:

The load force, 

3. Brownian Dynamics with Hydrodynamic Interactions
Consider a system of N spherical interacting Brownian particles suspended in a hydrodynamic medium, the displacement of particle 


where the superscript “0” indicates that the variable is to be evaluated at the beginning of the time step. 










In our case of a dimer in three dimensions the tensor 

A first basic quantity of interest, in our case, is the average center of mass velocity in the 


where
Another quantity of central interest will be the effective diffusion coefficient,

where
The competition between the drift 



here 


4. Results
We performed the simulation in dimensionless units. Distance is in units of the separation distance 






















The average velocity of a molecular motor is a function of the load force resisting the motor’s advancement. One of the characteristic of a molecular motor is the load force-velocity curve. In Figure 2 we show 




In the range 
In Figure 3, we observe the behaviour of the mass center position variance, 
as a function of time in the long time limit, i.e., after transients due to initial conditions have died out. The effective diffusion coefficient is giving by the slope of the linear fitting, 
In Figure 4 is shown the effective diffusion coefficient as a function of the load force, 

Figure 2. Mean 


Figure 3. Variance of the mass center position, 


Figure 4. The effective diffusion coefficient as a function of the load force, 

In Figure 5 is shown the Péclet number as a function of the load force, 

Figure 5. Péclet number as a function of the load force, 

Figure 6. Mean 


In Figure 6 is shown the mean x component of the mass center position as a function of time, 
time, in the long-time limit, for a given load force,

case with hydrodynamic interactions greater than the case without them.
In Figure 7 we observe the behaviour of the average center of mass velocity in the 


In Figure 8 is shown the spatial cross correlations in x direction as a function of Lag time, 
Figure 7. Mean 


Figure 8. Spatial cross correlations in 


A similar result was found by Houtman et al. [28] who developed a simple 2D-lattice model in order to test the influence of hydrodynamic interactions on the collective transport of molecular motors, which is important for the understanding of cell growth and development. Houtman et al. showed that long range collective hydrodynamic interactions lead to a substantial increase in the effective velocity of motors attached to a filament. Their results were also supported by experiments.
5. Conclusion
In conclusion, hydrodynamic interactions influence substantially the dynamics of a ratchet dimer Brownian motor; consequently they have to be considered in any theory where the molecular motors are in a liquid medium.
Cite this paper
José A.Fornés, (2015) Hydrodynamic Interactions Introduce Differences in the Behaviour of a Ratchet Dimer Brownian Motor. Journal of Biomaterials and Nanobiotechnology,06,81-90. doi: 10.4236/jbnb.2015.62008
References
- 1. Reimann, P. and Hanggi, P. (2002) Introduction to the Physics of Brownian Motors. Applied Physics A: Materials Science & Processing, 75, 169-178.
http://dx.doi.org/10.1007/s003390201331 - 2. Wang, H.Y. and Bao, J.D. (2004) The Roles of Ratchet in Transport of Two Coupled Particles. Physica A: Statistical Mechanics and Its Applications, 337, 13-26.
http://dx.doi.org/10.1016/j.physa.2004.01.031 - 3. Wang, H.Y. and Bao, J.D. (2005) Cooperation Behavior in Transport Process of Coupled Brownian Motors. Physica A: Statistical Mechanics and Its Applications, 357, 373-382.
http://dx.doi.org/10.1016/j.physa.2005.01.059 - 4. Wang, H.Y. and Bao, J.D. (2007) Transport Coherence in Coupled Brownian Ratchet. Physica A: Statistical Mechanics and Its Applications, 374, 33-40.
http://dx.doi.org/10.1016/j.physa.2006.07.005 - 5. Fornés, J.A. (2005) An Oscillating Electric Field with Thermal Noise Increases the Rotational Diffusion and Drives Rotation in a Dipole. Journal of Colloid and Interface Science, 281, 236-239.
http://dx.doi.org/10.1016/j.jcis.2004.08.088 - 6. von Gehlen, S., Evstigneev, M. and Reimann, P. (2008) Dynamics of a Dimer in a Symmetric Potential: Ratchet Effect Generated by an Internal Degree of Freedom. Physical Review E, 77, Article ID: 031136.
http://dx.doi.org/10.1103/PhysRevE.77.031136 - 7. Lipowsky, R., Chai, Y., Klumpp, S., Liepelt, S. and Müller, M.J.I. (2006) Molecular Motor Traffic: From Biological Nanomachines to Macroscopic Transport. Physica A: Statistical Mechanics and Its Applications, 372, 34-51.
http://dx.doi.org/10.1016/j.physa.2006.05.019 - 8. Taoa, Y.G. and Kapralb, R. (2008) Design of Chemically Propelled Nanodimer Motors. Journal of Chemical Physics, 128, Article ID: 164518.
http://dx.doi.org/10.1063/1.2908078 - 9. Howard, J. (2001) Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associates, Massachusetts.
- 10. Block, S.M. (1995) Nanometres and Piconewtons: The Macromolecular Mechanics of Kinesin. Trends in Cell Biology, 5, 169-175.
http://dx.doi.org/10.1016/S0962-8924(00)88982-5 - 11. Visscher, K., Schnitzer, M.J. and Block, S.M. (1999) Single Kinesin Molecules Studied with a Molecular Force Clamp. Nature, 400, 184-189.
http://dx.doi.org/10.1038/22146 - 12. Schnitzer, M.J., Visscher, K. and Block, S.M. (2000) Force Production by Single Kinesin Motors. Nature Cell Biology, 2, 718-723.
http://dx.doi.org/10.1038/35036345 - 13. Speer, D., Eichhorn, R., Evstigneev, M. and Reimann, P. (2012) Dimer Motion on a Periodic Substrate: Spontaneous Symmetry Breaking and Absolute Negative Mobility. Physical Review E, 85, Article ID: 061132.
http://dx.doi.org/10.1103/PhysRevE.85.061132 - 14. Zimmermann, E. and Seifert, U. (2012) Efficiencies of a Molecular Motor: A Generic Hybrid Model Applied to the F1- ATPase. New Journal of Physics, 14, Article ID: 103023. http://dx.doi.org/10.1088/1367-2630/14/10/103023
- 15. Pinkoviezky, I. and Gov, N.S. (2013) Modelling Interacting Molecular Motors with an Internal Degree of Freedom. New Journal of Physics, 15, Article ID: 025009.
http://dx.doi.org/10.1088/1367-2630/15/2/025009 - 16. Ermak, D.L. and Mc Cammon, J.A. (1978) Brownian Dynamics with Hydrodynamic Interactions. The Journal of Chemical Physics, 69, 1352-1360.
http://dx.doi.org/10.1063/1.436761 - 17. Kemps, J.A.L. and Bhattacharjee, S. (2009) Particle Tracking Model for Colloid Transport near Planar Surfaces Covered with Spherical Asperities. Langmuir, 25, 6887-6997.
http://dx.doi.org/10.1021/la9001835 - 18. Günther, S. and Kruse, K. (2008) A Simple Self-Organized Swimmer Driven by Molecular Motors. Europhysics Letters, 84, Article ID: 68002.
http://dx.doi.org/10.1209/0295-5075/84/68002 - 19. Ramia, M., Tullock, D.L. and Phan-Thien, N. (1993) The Role of Hydrodynamic Interaction in the Locomotion of Microorganisms. Biophysical Journal, 65, 755-778.
http://dx.doi.org/10.1016/S0006-3495(93)81129-9 - 20. Kim, M.J. and Powers, T.R. (2004) Viscous Hydrodynamics of Rotating Helices. Physical Review E, 69, Article ID: 061910.
- 21. Fornés, J.A. (2010) Hydrodynamic Interactions Induce Movement against an External Load in a Ratchet Dimer Brownian Motor. Journal of Colloid and Interface Science, 341, 376-379. http://dx.doi.org/10.1016/j.jcis.2009.09.057
- 22. Machura, L., Kostur, M., Marchesoni, F., Talkner, P., H?nggi, P. and Luczka, J. (2005) Optimal Strategy for Controlling Transport in Inertial Brownian Motors. Journal of Physics: Condensed Matter, 17, S3741-S3752.�
- 23. Grimm, A. and Stark, H. (2011) Hydrodynamic Interactions Enhance the Performance of Brownian Ratchets. Soft Matter, 7, 3219-3227.
http://dx.doi.org/10.1039/C0SM01085E - 24. Polson, J.M., Bylhouwer, B., Zuckermann, M.J., Horton, A.J. and Scott, W.M. (2010) Dynamics of a Polymer in a Brownian Ratchet. Physical Review E, 82, Article ID: 051931.
http://dx.doi.org/10.1103/PhysRevE.82.051931 - 25. Dickinson, E. (1985) Brownian Dynamic with Hydrodynamic Interactions: The Application to Protein Diffusional Problems. Chemical Society Reviews, 14, 421-455.
http://dx.doi.org/10.1039/cs9851400421 - 26. Doi, M. and Edwards, S.F. (1986) The Theory of Polymer Dynamics. Claredon Press, Oxford.
- 27. Freund, J.A. and Schimansky-Geier, L. (1999) Diffusion in Discrete Ratchets. Physical Review E, 60, 1304.
http://dx.doi.org/10.1103/PhysRevE.60.1304 - 28. Houtman, D., Pagonabarraga, I., Lowe, C.P., Esseling-Ozdoba, A., Emons, A.M.C. and Eiser, E. (2007) Hydrodynamic Flow Caused by Active Transport along Cytoskeletal Elements. Europhysics Letters, 78, Article ID: 18001.
http://dx.doi.org/10.1209/0295-5075/78/18001
NOTES
*On leave from Instituto de Física, Universidade Federal de Goiás, Goiânia, Brazil.











