Journal of Information Security
Vol. 3 No. 3 (2012) , Article ID: 21337 , 4 pages DOI:10.4236/jis.2012.33022
The Extended Tanh Method for Compactons and Solitons Solutions for the CH(n,2n – 1,2n,–n) Equations
School of Mathematics and Computing Science, Guilin University of Electronic Technology, Guilin, China
Email: {*lxq, tangsq}@guet.edu.cn, huangwentao@163.com
Received March 21, 2012; revised April 28, 2012; accepted May 10, 2012
Keywords: The CH(n,2n – 1,2n,–n) Equation; Compactons; Sine-Cosine Method and the Extended Tanh Method; Rational Hyperbolic Functions Method
ABSTRACT
In this paper, by using the sine-cosine method, the extended tanh-method, and the rational hyperbolic functions method, we study a class of nonlinear equations which derived from a fourth order analogue of generalized Camassa-Holm equation. It is shown that this class gives compactons, solitary wave solutions, solitons, and periodic wave solutions. The change of the physical structure of the solutions is caused by variation of the exponents and the coefficients of the derivatives.
1. Introduction
Recently, S. Tang [1] studied the nonlinear dispersive variants the CH(n,n,m) of the generalized Camassa-Holm equation in (1 + 1), (2 + 1) and (3 + 1) dimensions respectively by using sine-cosine method, it is shown that this class gives compactons, conventional solitons, solitary patterns and periodic solutions.
It is the objective of this work to further complement our studies in [1] on the CH(n,n,m) equation. Our first interest in the present work being in implementing the tanh method [2,3] to stress its power in handling nonlinear equations so that one can apply it to models of various types of nonlinearity. The next interest is the determination of exact travelling wave solutions with distinct physical structures to the CH(n,2n – 1,2n,–n) given by
 (1.1)
(1.1)
in (3 + 1) dimensions. Our approach depends mainly on the sine-cosine method [4], the tanh method [2,3], and the rational hyperbolic functions method [5] that have the advantage of reducing the nonlinear problem to a system of algebraic equations that can be solved by using Maple or Mathematica. As stated before, our approach depends mainly on the sine-cosine method, the extended tanh method, and the rational hyperbolic functions method. In what follows, we highlight the main steps of the proposed methods.
2. Analysis of the Methods
For the three methods, we first use the wave variable  to carry a PDE in two independent variables
to carry a PDE in two independent variables
 (2.1)
(2.1)
into an ODE
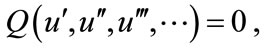 (2.2)
(2.2)
Equation (2.2) is then integrated as long as all terms contain derivatives where integration constants are considered zeros.
2.1. The Sine-Cosine Method
The sine-cosine algorithm admits the use of the ansätz
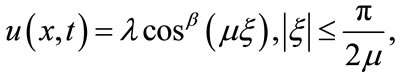 (2.3)
(2.3)
or the ansätz
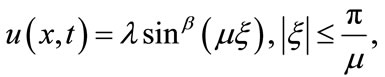 (2.4)
(2.4)
where 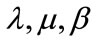 are parameters that will be determined.
are parameters that will be determined.
2.2. The Tanh Method
The standard tanh method introduced in [2,3] where the tanh is used as a new variable, since all derivatives of a tanh are represented by a tanh itself. We use a new independent variable
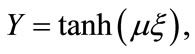 (2.5)
(2.5)
that leads to the change of derivatives:
 (2.6)
(2.6)
We then apply the following finite expansion:
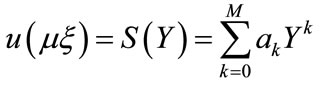 (2.7)
(2.7)
and
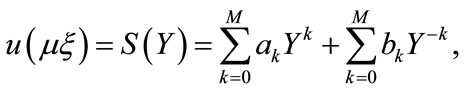 (2.8)
(2.8)
where M is a positive integer that will be determined to derive a closed form analytic solution.
2.3. The Rational Sinh Functions Method
It is appropriate to introduce rational hyperbolic functions methods where we set
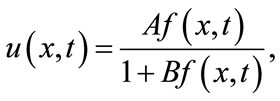 (2.9)
(2.9)
where  and
and  are parameters that will be determined, and
are parameters that will be determined, and
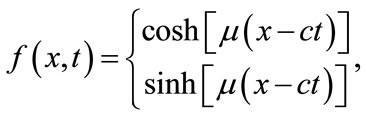 (2.10)
(2.10)
The rational hyperbolic functions methods can be applied directly in a straightforward manner. We then collect the coefficients of the resulting hyperbolic functions and setting it equal to zero, and solving the resulting equations to determine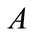 ,
, 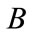 ,
, 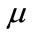 and
and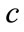 . This assumption will be used for the determination of solitons structures the CH(n, 2n – 1, 2n, –n) equations.
. This assumption will be used for the determination of solitons structures the CH(n, 2n – 1, 2n, –n) equations.
3. Using the Sine-Cosine Method
For the CH(n, 2n – 1, 2n, –n) equation given by (1.1), using the wave variable  carries (1.1) into the ODE, respectively
carries (1.1) into the ODE, respectively
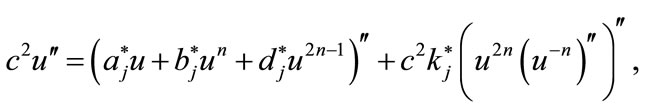 (3.1)
(3.1)
where
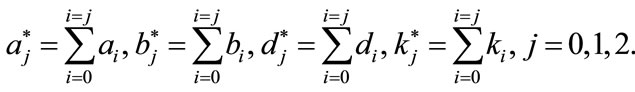 (3.2)
(3.2)
Integrating (3.1) twice, respectively, using the constants of integration to be zero we find
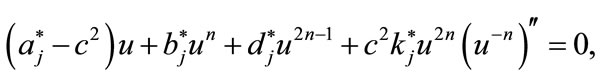 (3.3)
(3.3)
Substituting (2.3) into (3.3) gives
 (3.4)
(3.4)
Equation (3.4) is satisfied only if the following system of algebraic equations holds:
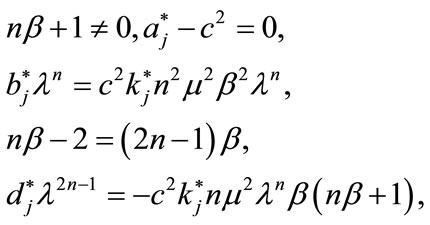 (3.5)
(3.5)
Solving the system (3.5) gives
 (3.6)
(3.6)
The results (3.6) can be easily obtained if we also use the sine method (2.4). Combining (3.6) with (2.3) and (2.4), the following compactons solutions
 (3.7)
(3.7)
and
 (3.8)
(3.8)
are readily obtained, where
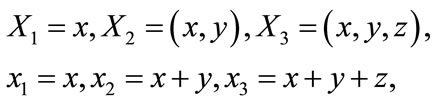 (3.9)
(3.9)
However, for  we obtain the following solitary wave solutions
we obtain the following solitary wave solutions
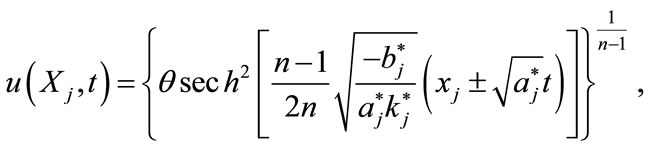 (3.10)
(3.10)
and
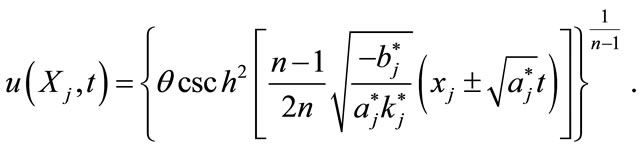 (3.11)
(3.11)
4. Using the Extended Tanh Method
Using the assumptions of the tanh method (2.5)-(2.7) gives
 (4.1)
(4.1)
To determine the parameter M we usually balance the linear terms of highest order in the resulting Equation (4.1) with the highest order nonlinear terms. This in turn gives
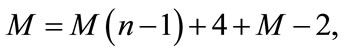 (4.2)
(4.2)
so that
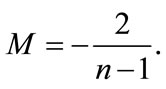 (4.3)
(4.3)
To get a closed form analytic solution, the parameter 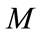 should be an integer. A transformation formula
should be an integer. A transformation formula
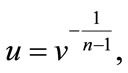 (4.4)
(4.4)
should be used to achieve our goal. This in turn transforms (3.6) to
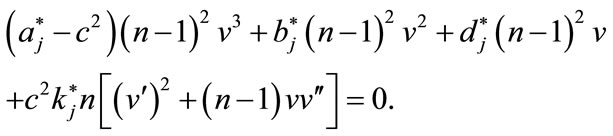 (4.5)
(4.5)
Balancing 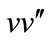 and
and 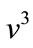 gives
gives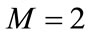 . The extended tanh method allows us to use the substitution
. The extended tanh method allows us to use the substitution
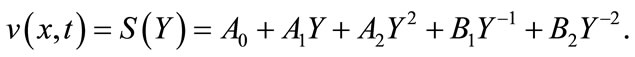 (4.6)
(4.6)
Substituting (4.6) into (4.5), collecting the coefficients of each power of 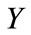 and using Mapple to solve the resulting system of algebraic equations we obtain the following three sets:
and using Mapple to solve the resulting system of algebraic equations we obtain the following three sets:

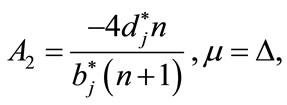
 (4.7)
(4.7)
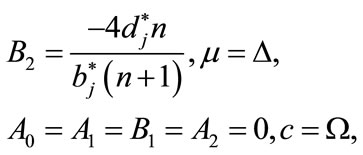 (4.8)
(4.8)
and
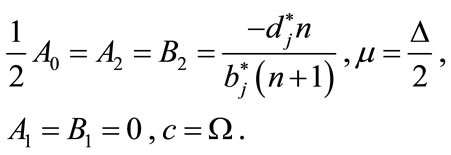 (4.9)
(4.9)
Noting that
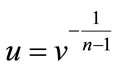 for
for

or
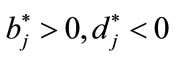 we obtain the solitary wave solutions
we obtain the solitary wave solutions
 (4.10)
(4.10)
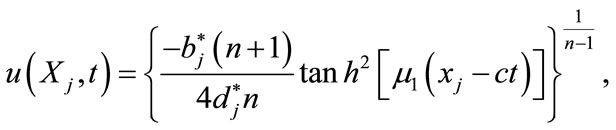 (4.11)
(4.11)
 (4.12)
(4.12)
where 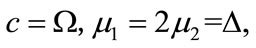
However, for
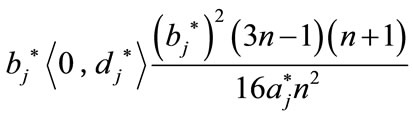 or
or
 we obtain the periodic solutions
we obtain the periodic solutions
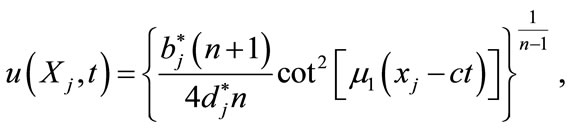 (4.13)
(4.13)
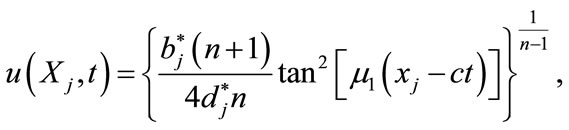 (4.14)
(4.14)
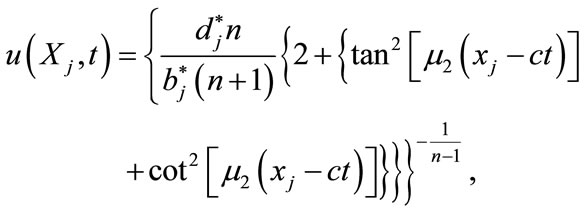 (4.15)
(4.15)
where 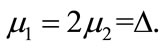

5. Using the Rational Sinh and Cosh Functions Methods
We now substitute the rational cosh
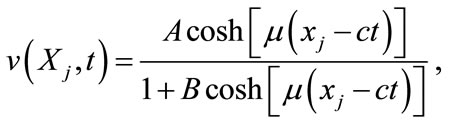 (5.1)
(5.1)
into (4.5), where
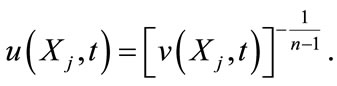 (5.2)
(5.2)
Collecting the coefficients of the like hyperbolic functions, and proceeding as before we find

 (5.3)
(5.3)
The results (5.2) can be easily obtained if we also use the rational sinh method. This gives the solitons solutions
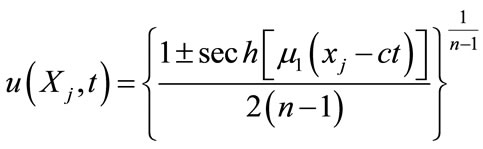 (5.4)
(5.4)
and
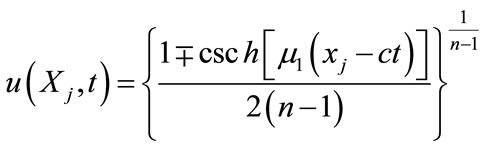 (5.5)
(5.5)
for , and the periodic wave solution
, and the periodic wave solution
 (5.6)
(5.6)
and the complex solution
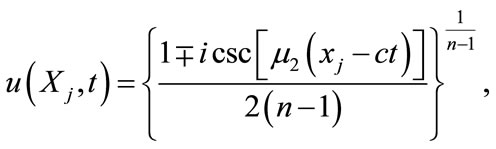 (5.7)
(5.7)
for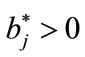 , where
, where
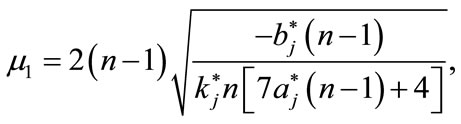
 .(5.8)
.(5.8)
6. Conclusion
The basic goal of this work has been to extend our work on the CH(n,n,m) equation in [1]. The sine-cosine method, the tanh method, and the rational hyperbolic functions method were used to investigate variants of the CH(n,2n – 1,2n,–n) equations. The study revealed compactons solutions, solitary wave solutions, solitons, and periodic wave solutions for all examined variants.
7. Acknowledgements
This research was supported by NNSF of China (110- 61010).
REFERENCES
- S. Tang, Y. Xiao and Z. Wang, “Travelling Wave Solutions for a Class of Nonlinear Fourth Order Variant of a Generalized Camassa-Holm Equation,” Applied Mathematics and Computation, Vol. 210, 2009, pp. 39-47. doi:10.1016/j.amc.2008.10.041
- W. Malfliet, “Solitary Wave Solutions of Nonlinear Wave Equations,” American Journal of Physics, Vol. 60, No. 7, 1992, pp. 650-654. doi:10.1119/1.17120
- W. Malfliet and W. Hereman, “The Tanh Method: II. Perturbation Technique for Conservative Systems,” Physica Scripta, Vol. 54, 1996, pp. 569-575.
- A. M. Wazwaz, “A Class of Nonlinear Fourth Order Variant of a Generalized Camassa-Holm Equation with Compact and Noncompact Solutions,” Applied Mathematics and Computation, Vol. 165, 2005, pp. 485-501. doi:10.1016/j.amc.2004.04.029
- Z. Y. Yan, “New Explicit Travelling Wave Solutions for Two New Integrable Coupled Nonlinear Evolution Equations,” Physics Letters A, Vol. 292, 2001, pp. 100-106. doi:10.1016/S0375-9601(01)00772-1
NOTES
*Corresponding author.

