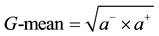Journal of Data Analysis and Information Processing
Vol.03 No.03(2015), Article ID:57803,6 pages
10.4236/jdaip.2015.33004
An Improved Algorithm for Imbalanced Data and Small Sample Size Classification
Yong Hu1*, Dongfa Guo1, Zengwei Fan1, Chen Dong1, Qiuhong Huang1, Shengkai Xie1, Guifang Liu1, Jing Tan1, Boping Li1, Qiwei Xie2
1Analytical Laboratory Beijing Research Institute of Uranium Geology, Beijing, China
2Department of Electronics and Information, Toyota Technological Institute, Nagoya, Japan
Email: *yonghu_iacas@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 June 2015; accepted 5 July 2015; published 8 July 2015
ABSTRACT
Traditional classification algorithms perform not very well on imbalanced data sets and small sample size. To deal with the problem, a novel method is proposed to change the class distribution through adding virtual samples, which are generated by the windowed regression over-sampling (WRO) method. The proposed method WRO not only reflects the additive effects but also reflects the multiplicative effect between samples. A comparative study between the proposed method and other over-sampling methods such as synthetic minority over-sampling technique (SMOTE) and borderline over-sampling (BOS) on UCI datasets and Fourier transform infrared spectroscopy (FTIR) data set is provided. Experimental results show that the WRO method can achieve better performance than other methods.
Keywords:
Class Imbalance Learning, Over-Sampling, High-Dimensional Small-Sample Size, Support Vector Machine

1. Introduction
Imbalanced data [1] sets can lead to the traditional data mining algorithms behaving undesirable, which is because the distribution of the data sets is not taken into consideration in the algorithms. Because of the extreme imbalance, a trivial learning algorithm may cause the decision boundary skewed toward the minority class, so the new minority test samples are likely to be misclassified. Various methods for dealing with this problem have been proposed recently. The first type of methods focuses on data processing: removing a number of samples from the majority class (under-sampling) or adding new samples into the minority class (over-sampling). The former methods [2] have drawbacks that they may lead to lose relevant information. The later method [3] is achieved by adding some synthetic samples until the desired class ratios are attained: Chawla et al. [3] over- sample the minority class through synthetic minority over-sampling technique (SMOTE) method. Nguyen et al. [4] propose borderline over-sampling (BOS) method in which only the minority samples near the borderline are over-sampled. The second type of methods focuses on modifying the existing classification algorithms. For support vector machines (SVM) method, proposals such as using different weighting constants for different classes [5] , or adjusting the class boundary based on kernel-alignment ideal [6] are reported. Huang et al. [7] present biased minimax probability machine (BMPM) to resolve the imbalanced problem. Furthermore, there are other effective methods such as cost-sensitive learning [8] and one-class learning [9] .
In the particular tasks such as face recognition (FR) [10] , the number of available training samples is usually much smaller than the dimensionality of the samples pace. Consequently, the biggest challenge that all linear discriminant analysis (LDA)-based approaches have to face is the “small sample size” (SSS) problem. These are often ill-posed problems. There are many ways to address the problem: One option is to apply linear algebra techniques to solve the numerical problem of inverting the singular within class scatter (WCS) matrix. The second option is the feature extraction-based methods, such as the well-known fisher faces method [11] . However, the discarded null space may contain significant discriminatory information, and this will further effect the formation of classifier. The third option is over-sampling method: we can over-sample the training samples so that the number of samples is comparable with the dimensionality of the samples pace, which will make the WCS nonsingular.
We solve the imbalanced problem and SSS problem based on data processing. To deal with the two problems, we propose a windowed regression over-sampling (WRO) method. In this method, the virtual samples are generated according to the difference between adjacent samples. In contrast to SMOTE and BOS methods, the difference is estimated in a local window with the least square regression instead of the whole ones. Moreover, both additive and multiplicative effects between samples are considered in WRO algorithm.
2. Weighting Support Vector Machines for Classification
The objective of the training of SVM is to find the optimal hyperplane that separates the positive and negative
classes with a maximum margin [12] . Consider the training set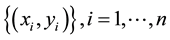 , where
, where 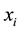 is a training
is a training
sample and 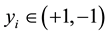 is its corresponding true label. To solve the imbalanced datasets, Veropoulos et al. [5] suggested using different weighting constants for the minority and majority classes in SVM (Weighting SVM: WSVM):
is its corresponding true label. To solve the imbalanced datasets, Veropoulos et al. [5] suggested using different weighting constants for the minority and majority classes in SVM (Weighting SVM: WSVM):
Minimize:
 (1)
(1)
Subject to:
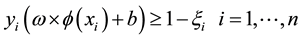 (2)
(2)
where  and b are the weight vector and the bias of the hyperplane respectively,
and b are the weight vector and the bias of the hyperplane respectively, 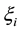 indicates degree of location violation of the i-th training sample,
indicates degree of location violation of the i-th training sample,  and
and  are the different error costs for the minority and major-
are the different error costs for the minority and major-
ity classes.  is akernel function that enables to compute dot products in the feature
is akernel function that enables to compute dot products in the feature
space without knowing the mapping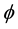 . In this paper, we use the RBF kernel as follows:
. In this paper, we use the RBF kernel as follows:
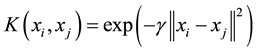 (3)
(3)
where 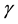 is a width parameter, control the radial scope. There are no guidelines for deciding what the relative ratios of the minority to majority cost factors should be, we empirically set the cost ratio to the inverse of the imbalance ratio and that is what we have used in this paper. However, WSVM is sensitive to the minority samples and obtains stronger cues from the minority samples about the orientation of the plane than from the majority samples. If the minority samples are sparse, as in imbalanced datasets, then the boundary may not have the proper shape in the input space [13] .
is a width parameter, control the radial scope. There are no guidelines for deciding what the relative ratios of the minority to majority cost factors should be, we empirically set the cost ratio to the inverse of the imbalance ratio and that is what we have used in this paper. However, WSVM is sensitive to the minority samples and obtains stronger cues from the minority samples about the orientation of the plane than from the majority samples. If the minority samples are sparse, as in imbalanced datasets, then the boundary may not have the proper shape in the input space [13] .
3. The Proposed Algorithm
To solve the imbalanced problem, an appropriate number of virtual samples are added to the minority class according to the sampling level; to solve the SSS problem, we generate virtual samples so that the size and the dimensionality of training samples are comparable to a certain extent. The basic idea is as follows:
Let  be a samples matrix whose rows and columns correspond to samples and variables respectively. Denote the n samples as
be a samples matrix whose rows and columns correspond to samples and variables respectively. Denote the n samples as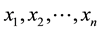 , we produce more virtual samples in the dense region and less in the sparse region: calculating the mean of the samples in the category and denoting it as x, then computing the distance between the mean value and each sample
, we produce more virtual samples in the dense region and less in the sparse region: calculating the mean of the samples in the category and denoting it as x, then computing the distance between the mean value and each sample 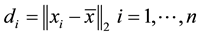 and obtaining the normalized weight vector
and obtaining the normalized weight vector 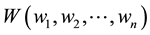
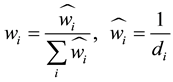
the weight 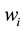
Given the sampling level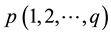
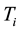

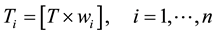
where 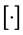
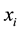
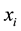
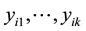
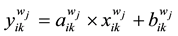
where 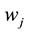
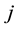
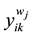
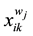
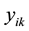
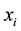
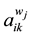
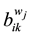
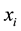
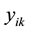
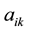
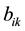
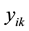
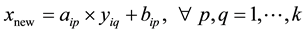
The WRO algorithm is therefore summarized as follows:
Many over-sampling algorithms such as SMOTE and BOS only reflect the additive effect between each sample, while our algorithm WRO also reflects multiplicative effect all together from Equation (7) and all of these effect are computed in a local region rather than in a whole region. WRO can enlarge the decision regions and also improve the prediction of the minority class while not sacrificing the accuracy of the whole testing set.
4. Materials
Two data sets from the UCI machine learning repository [15] including Glass (7) and Yeast (5) are used in the experiments. Numbers in parentheses indicate which class is chosen as minority class and all of the remaining classes are combined to create a majority class. We also use 500 Fourier Transform infrared (FTIR) spectra as
Figure 1. Obtain regression coefficient with the sliding window between samples.
small size data sets. The FTIR spectra in the region 4000 - 650 cm-1 have been recorded with a Perkin-Elmer Spectrum GX FTIR spectrometer, equipped with the Universal ATR sampling accessory. The details of UCI data sets and FTIR dataset are provided in Table 1. “Imbalance” indicates the ratio between the majority class and the minority class.
5. Experimental Results
The programs are written in house in Matlab Version R2012a and run in a personal computer with a 2.20 GHz Intel Core 2 processor, 4 GB RAM, and a Windows 7 operating system.
5.1. Evaluation Measures
The evaluation measures used for imbalanced samples classification in our experiments are based on the confusion matrix [16] . Table 2 illustrates a confusion matrix for a two class problem with positive (minority) and negative (majority). With this matrix, our performance measures are expressed:
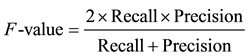
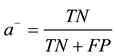
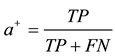
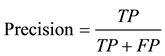
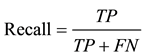

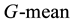
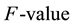
5.2. Experimental Results and Discussions
For imbalanced datasets, we compare the proposed method WRO with WSVM [5] method and some other over-sampling methods including SMOTE and BOS. For SSS problem, we compare the proposed method WRO with standard SVM and PCA feature extraction-based method. The code for SVM and WSVM are taken from the package LIBSVM [17] and the Gaussian RBF kernel is used in the next experiment. We empirically set 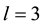
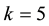
the effect of randomness in the division of data and sampling, each method is run ten times and then the average performance is calculated. Each time consists of: 1) randomly splitting the two classes samples into training and testing sets with the ratio 7.5:2.5; 2) for imbalanced problem, over-sampling the minority class samples on training data with different methods, for SSS problem, over-sampling the two class samples on the training data with different methods; 3) performing 5-fold cross-validation on the over-sampled training data to estimate the optimal parameters 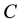
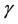
Results for Glass are shown in Figure 2, we can see that the proposed method WRO achieves a better result in terms of 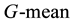
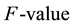
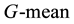
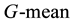
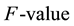
Figure 4 shows the SSS classification problem, the dimensionality of the sample space is much higher than the
Table 1. Data sets used for the experiment.
Table 2. Two-class confusion matrix.
Figure 2. G-mean and F-value performance on the Glass at different sampling level.
Figure 3. G-mean and F-value performance on the yeast at different sampling levels.
Figure 4. Accuracy on the FTIR at different sampling level.
amount of training samples. Without over-sampling for the training set, the prediction accuracy with SVM is about 86%. After performed with PCA, we used the first ten features, and the prediction accuracy with SVM is about 88% in this case. While the accuracy is improved with SMOTE and WRO methods through an appropriate oversampling level. We can see that the selection of the over-sampling level p impacts on the prediction accuracy of different over-sampling methods, when p is small, we can get better neighbors for the over-sampling process, so the prediction accuracy can be dramatically improved, when p is large enough, more noise is likely to be introduced, so a larger training samples are generated with over-sampling method and less information is lost. Consequently, p is a tradeoff between inducing more noise and losing less information. Nonetheless, our method WRO is comparable with SMOTE method with almost all p values.
6. Conclusion
In this paper, we have addressed the imbalanced data and SSS classification problem. To solve these problems, we propose a new over-sampling method based on windowed regression. Experimental results on two UCI data sets and one FTIR data set demonstrate the efficiency of the proposed algorithm. Of course, there are too many parameters in the algorithm. Meanwhile, the method of solving regression coefficients is in the local window, so the efficiency is not high, and we are going to study all of these.
Acknowledgements
The author thanks for the support by the Core Ability Promotion Project of China National Nuclear Corporation (HXF111-1) and the National Natural Science Foundation of China (61101219).
References
- Zheng, Z.H., Wu, X.Y. and Srihari, R. (2004) Feature Selection for Text Categorization on Imbalanced Data. ACM SIGKDD Explorations Newsletter, 6, 80-89. http://dx.doi.org/10.1145/1007730.1007741
- Xie, J.G. and Qiu, Z.D. (2007) The Effect of Imbalanced Data Sets on LDA: A Theoretical and Empirical Analysis. Pattern Recognition, 40, 557-662. http://dx.doi.org/10.1016/j.patcog.2006.01.009
- Chawla, N. (2003) C4.5 and Imbalanced Data Sets: Investigating the Effect of Sampling Method, Probabilistic Estimate and Decision Tree Structure. Workshop on Learning from Imbalanced Datasets II, ICML, Washington DC.
- Nguyen, H.M., Cooper, E.W. and Kamei, K. (2011) Borderline Over-Sampling for Imbalanced Data Classification. International Journal of Knowledge Engineering and Soft Data Paradigms, 3, 4-21. http://dx.doi.org/10.1504/IJKESDP.2011.039875
- Veropoulos, K., Campbell, C. and Cristianini, N. (1999) Controlling the Sensitivity of Support Vector Machines. Proceedings of the International Joint Conference on AI, 55-60.
- Wu, G. and Chang, E.Y. (2003) Class-Boundary Alignment for Imbalanced Dataset Learning. Workshop on Learning from Imbalanced Datasets II, ICML, Washington DC.
- Huang, K.Z. and Yang, H.Q. (2004) Learning Classifiers from Imbalanced Data Based on Biased Minimax Probability Machine. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2, 558-563.
- Zhou, Z.H. and Liu, X.Y. (2006) Training Cost-Sensitive Neural Networks with Methods Addressing the Class Imbalance Problem. IEEE Transactions on Knowledge and Data Engineering, 18, 63-77. http://dx.doi.org/10.1109/TKDE.2006.17
- Manevitz, L.M. and Yousef, M. (2002) One-Class SVMs for Document Classification. Journal of Machine Learning Research, 2, 139-154.
- Samal, A. and Iyengar, P.A. (1992) Automatic Recognition and Analysis of Human Faces and Facial Expressions: A Survey. Pattern Recognition, 25, 65-77. http://dx.doi.org/10.1016/0031-3203(92)90007-6
- Belhumeur, P.N., Hespanha, J.P. and Kriegman, D.J. (1997) Eigenfaces vs. Fisherfaces: Recognition Using Class Specific Linear Projection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 19, 711-720. http://dx.doi.org/10.1109/34.598228
- Vapnik, V.N. (2000) The Nature of Statistical Learning Theory. 2nd Edition, Springer, Berlin. http://dx.doi.org/10.1007/978-1-4757-3264-1
- Akbani, R., Kwek, S. and Japkowicz, N. (2004) Applying Support Vector Machines to Imbalanced Datasets. Machine Learning: ECML 2004. Springer, Berlin, 39-50. http://dx.doi.org/10.1007/978-3-540-30115-8_7
- Luo, J.W., Ying, K. and Bai, J. (2005) Savitzky-Golay Smoothing and Differentiation Filter for Even Number Data. Signal Processing, 85, 1429-1434. http://dx.doi.org/10.1016/j.sigpro.2005.02.002
- Asuncion, A. and Jnewman, D. (2007) UCI Machine Learning Repository.
- Kubat, M. and Matwin, S. (1997) Addressing the Curse of Imbalanced Training Sets: One-Sided Selection. Proceedings of the 14th International Conference on Machine Learning, 179-186.
- Chang, C.C. and Lin, C.J. (2011) LIBSVM: A Library for Support Vector Machines. ACM Transactions on Intelligent Systems and Technology (TIST), 2, 1-27. http://dx.doi.org/10.1145/1961189.1961199
NOTES
*Corresponding author.