Journal of Data Analysis and Information Processing
Vol.03 No.02(2015), Article ID:56199,8 pages
10.4236/jdaip.2015.32002
Comparison of Feature Reduction Techniques for the Binominal Classification of Network Traffic
Adel Ammar
College of Computer and Information Sciences, Computer Sciences Department, Al Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia
Email: Adel.Ammar@ccis.imamu.edu.sa
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 March 2015; accepted 5 May 2015; published 8 May 2015
ABSTRACT
This paper tests various scenarios of feature selection and feature reduction, with the objective of building a real-time anomaly-based intrusion detection system. These scenarios are evaluated on the realistic Kyoto 2006+ dataset. The influence of reducing the number of features on the classification performance and the execution time is measured for each scenario. The so-called HVS feature selection technique detailed in this paper reveals many advantages in terms of consistency, classification performance and execution time.
Keywords:
Intrusion Detection, Network Security, Feature Selection, Kyoto Dataset, Neural Networks, PCA, PLS

1. Introduction
For Intrusion Detection Systems (IDS), ranking the importance of input features is a problem of significant interest, since the elimination of irrelevant or useless inputs leads to a simplification of the problem and may allow faster and more accurate detection. For that aim, machine learning techniques play a very important role in information security to classify data as legitimate or normal data, and to select the most relevant features. A machine learning-based approach is one of the feasible heuristic methods to solve complicated problems for which a human designer is unable to define the appropriate rules or control laws in an explicit form. This is especially critical for the construction of an efficient real-time IDS which is able to comply with the constraints of high speed networks. In this work, we compared several feature selection or feature reduction techniques, organized in multistep scenarios. Their evaluation is based on assessing the loss of accuracy yielded by a classifier using the information of the reduced set of inputs, compared to a classifier using the full information of all original features. The evaluation was made over the realistic Kyoto 2006+ network traffic dataset.
2. Dataset
2.1. Original Dataset: Kyoto 2006+
The Kyoto 2006+ [1] is an evaluation dataset of network detection mechanism obtained from diverse honeypots from November 2006 to August 2009. This dataset captures the real network traffic without any human alteration or deletion. It encompasses the recent trends of network attacks distinguished from normal traffic via the use of honeypots. It consists of 24 statistical features where 14 conventional features are extracted from KD- DCUP’99 dataset [2] , and 10 additional features are added that may enable to investigate more effectively what kind of attacks happened in the networks. In the present study, we have discarded the features of IDS_detection, Malaware_detection and Ashula_detection since they are prediction labels. We have also discarded IP_source and IP_destination since they are network-dependent and have extremely large range of values. This gives us 18 input features that are summarized in Annex I.
The Kyoto dataset is labeled; the label indicates whether the session is an attack or not. In the original database, there are three labels: “1” (normal session); “−1” (known attack), and “−2” (unknown attack). Nevertheless, since the unknown attacks in the database are extremely rare (0.7%), which makes them very difficult to detect for a machine learning model, we attribute a same label for known and unknown attacks, so that the problem becomes a binary classification.
2.2. Randomly Extracted Learning and Validation Datasets
We randomly extracted 70 samples from each day, using a simple random sampling, out of the original Kyoto database, which constitutes 78,400 samples. Then we subdivided this database into 3 randomly extracted sets:
- Learning dataset: 20% (15,680 samples). The learning dataset is used to train the neural networks, through an iterative modification of the connection weights, using the back-propagation algorithm.
- Single-split validation dataset: 20% (15,680 samples), used for validating the learning, in order to avoid over-fitting (fitting to noise). The classification error on the validation database is calculated at each training iteration. When this error increases, the training process is stopped, even if the error on the learning dataset continues to decrease. The validation database does not participate, however, to the modification of the con- nection weights. After the training, the performance on the validation dataset is used to select the best neural network architecture (see Section 3.4.1).
- Testing dataset: 60% (47,040 samples). These samples do not participate to the training process in any way. They are only used for the final performance assessment. Thus, they give a closest insight into the real per- formance and generalization capability of the model on new unseen data.
3. Machine Learning Models
Increasing interest in machine learning has led to the development of numerous learning algorithms, most of which are designed with the aim of improving the existing ones. A learning machine uses data to find the appro- ximating function (in regression problems) or the separation boundary (in classification and pattern recognition problems). In order to optimize the performance of the machine learning model used for classifying the network traffic, in terms of accuracy and execution time, we present in this section different techniques for reducing the number of features on the input of the classification models.
3.1. Preprocessing
Normalization: Raw data generally need to be preprocessed before being fed to the input of a machine learning model. The most used preprocessing technique is normalization; for each feature i, mean value mi and standard deviation si are calculated on the set of learning and validation datasets (31,360 samples). Then, for each sample j of the three databases (learning, validation and test), 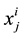 (value of the feature i for the sample j) is replaced by:
(value of the feature i for the sample j) is replaced by:
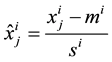 (1)
(1)
The main advantage of normalization is to avoid attributes in greater numeric ranges artificially dominating those in smaller numeric ranges. The values ranges of the attributes are scaled to give all features an equal a priori weight.
3.2. PCA
Principal component analysis (PCA) is a multivariate statistical technique used for feature reduction. PCA aims at:
(1) extracting the most important information from the dataset;
(2) compressing the size of the data set by keeping only the most important information (feature reduction);
(3) simplifying the description of the data set by means of a set of statistically uncorrelated features;
(4) analyzing the structure of the observations and the variables [3] .
In order to achieve these goals, PCA computes new variables called principal components which are obtained as linear combinations of the original variables. The first principal component is required to have the largest possible variance (i.e. inertia and therefore this component will “explain” or “extract” the largest part of the inertia of the dataset). The second component is computed under the constraint of being orthogonal to the first component and to have the largest possible inertia. The other components are computed likewise. The values of these new variables for the observations are called factor scores and can be interpreted geometrically as the projections of the observations onto the principal components [3] .
Before applying PCA, data must be centered (to mean 0), and is also generally normalized in order to avoid attributes in greater numeric ranges artificially dominating those in smaller numeric ranges.
Despite its popularity, PCA suffers from a lack of interpretability of the principal components since they are linear combinations of the original features, and generally do not have any physical meaning, especially when large numbers of features are involved.
3.3. Weighted PCA
The main idea of the weighted PCA is to give the original features different weights according to their impor- tance, measured by a feature ranking technique, in the scope of solving the binary classification problem of dis- tinguishing normal traffic from attacks.
The input feature contributions (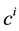 ) are measured using HVS technique (see Section 3.4). Then for each sample j of the three databases (learning, validation and test),
) are measured using HVS technique (see Section 3.4). Then for each sample j of the three databases (learning, validation and test), 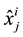 (normalized value of the feature i for the sample j) is replaced by:
(normalized value of the feature i for the sample j) is replaced by:
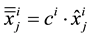 (2)
(2)
3.4. Neural Networks
The development of artificial neural networks (ANN or simply NN) arose from the attempt to simulate biological nervous systems by combining many simple computing elements (neurons) into a highly inter-connected system. The alleged intelligence of artificial neural networks is, however, a matter of dispute. An artificial neural network consists of an interconnected group of artificial neurons, and it processes information using a connectionist approach to computation. In most cases, an ANN is an adaptive system that changes its parameters based on external or internal information that flows through the network during the learning phase. Neural networks are usually used to model complex relationships between inputs and outputs or to find patterns in data.
We used a feed-forward neural network (also called multi-layer perceptron (MLP)) trained by a back propagation algorithm. An MLP is an artificial neural network where connections between the units do not form a directed cycle. In this network, the information moves in only one direction, forward, from the input nodes, through the hidden nodes to the output nodes. There are no cycles or loops in the network. Except for the input nodes, each node is a neuron (or processing element) with a nonlinear activation function. Generally, the units of these networks (including the output neuron) apply a sigmoid function (hyperbolic tangent) as an activation function. MLP utilizes back propagation for training the network. Back propagation algorithm is a supervised learning method which can be divided into two phases: propagation and weight update. The two phases are repeated until the performance of the network is good enough, or until convergence. In back propagation algorithms, the output values are compared with the correct answer to compute the value of some predefined error-function. The error is then fed back through the network. Using this information, the algorithm adjusts the weights of each connection in order to reduce the value of the error function by some small amount. After repeating this process for a sufficiently large number of training cycles, the network will usually converge to some state where the error of the calculations is small.
The number of input nodes is Nf + 1, where Nf is the number of input features, while the output is a single neuron for the present binominal classification problem.
To get a more accurate classification model from MLP, input features are normalized. Normalization is a pre- processing step performed before learning. The main advantage of this step is to avoid attributes in greater numeric ranges artificially dominating those in smaller numeric ranges.
The MLP classifier cannot handle nominal attributes, it can only classify using numerical attributes. Thus, nominal attributes such as port number is considered as a numerical value.
3.4.1. Neural Networks’ Architecture
In the following experiments, we used networks with only one hidden layer. In fact, [4] have shown that “multilayer feed-forward networks with as few as one hidden layer using arbitrary squashing functions are capable of approximating any Borel measurable function from one finite dimensional space to another to any desired degree of accuracy, provided sufficiently many hidden units are available. In this sense, multilayer feed-forward networks are a class of universal approximators”, and they can form disjoint decision regions with arbitrary shapes in multidimensional cases [5] .
Various numbers of hidden neurons, in the single hidden layer, have been tested for each scenario, and the number that maximizes the accuracy over the validation dataset has been retained.
3.4.2. Post-Processing: Discretization
Since the transition function of the output neuron is a sigmoid, the raw prediction will be a real value between −1 and 1. This value is then discretized to obtain a binary prediction (−1: attack or 1: normal). This is simply made using a threshold, which is generally chosen to be 0, unless one wants to obtain a different trade-off between false positives and false negatives; to reduce the false positive rate (at the expense of a higher false negative rate), the threshold should be less than 0, and vice versa. In all the following experiments, the threshold has been fixed to 0.
3.5. NN-Based HVS Feature Selection Technique
The method we proposed for selecting connection features is based on feed-forward neural networks. It has been first applied in geoscience by [6] and was theoretically formulated by [7] who called it HVS (Heuristic for Variable Selection).
We introduce the features that need to be ranked as inputs of a feed-forward neural network (with a single hidden layer) used as a classifier that distinguishes attacks from normal traffic. After the training process on a representative learning database, we assess the relative contribution of each feature as follows.
We calculate the contribution Cjs of a neuron j of the hidden layer to the output s according to the following formula:
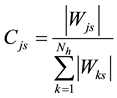 (3)
(3)
where Wks is the weight of the connection between a hidden neuron k and the output s and Nh is the number of hidden neurons. Then, we obtain the contribution of an input neuron i to the output according to the following formula:
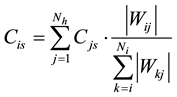 (4)
(4)
where Wij is the weight of the connection between the input neuron i and a hidden neuron j, and Ni is the number of inputs. The sum of input contributions is therefore equal to 1.
Note that (3) and (4) can be generalized to multiple outputs and multiple hidden layers and reduced to a single recursive formula if we define the contribution of output neurons as being equal to 1, according to the following algorithm:
Contribution(neuron_i, layer_j) // neuron_i belongs to layer_j
If layer_j=number_of_layers then return 1; // Output layer
C=0;
For k=1 to number_neurons(layer_i+1)
// Layers are numbered ascendingly from input to output
C = C + weight(neuron_i, neuron_k) / sum_weights(layer_i, neuron_k) * Contribution(neuron_k, layer_i+1);
End
Return C;
End
Note that the inputs features must be normalized before applying HVS in order to avoid attributes in greater numeric ranges artificially dominating those in smaller numeric ranges.
3.6. Partial Least Squares Regression (PLS)
3.6.1. Principle
PLS is a bilinear statistical method that was first introduced by [8] . It focuses on maximizing the variance of the dependent variables explained by the independent ones instead of reproducing the empirical covariance matrix. A PLS model consists of a structural part, which reflects the relationships between the latent variables, a measurement component, which shows how the latent variables and their indicators are related, and a third component, which is the weight relations used to estimate case values for the latent variables. First, the weight relations, which link the indicators to their respective unobservable variables, are estimated. Second, case values for each unobservable variable are calculated, based on a weighted average of its indicators, using the weight relations as an input. Finally, these case values are used in a set of regression equations to determine the parameters for the structural relations [9] .
3.6.2. Post-Processing: Discretization
PLS is primarily used for regression problems. In order to apply it to our binominal classification problem, a thres- hold is applied in the same way as explained in Section 3.4.2.
4. Modeling Scenarios
In order to compare the machine learning techniques described above in various configurations, we have tested 13 different scenarios. Letter “a” refers to a model that takes the whole 18 inputs, letter “b” indicates a model using a reduced feature set of 5 inputs, and letter “c” is a model using a reduced feature set of only 3 inputs.
・ Scenario 1a: Original 18 features
A Neural Network is trained with the original 18 features as inputs.
Pre-processing: Normalization only.
・ Scenario 1b: 5 features selected by HVS
After training following Scenario 1a, the input feature contributions are measured using HVS technique. We select the 5 features having the highest contributions to put as inputs of a new neural network.
Pre-processing: Normalization only.
・ Scenario 2a: 18 PCA components
A Neural Network is trained using the 18 PCA components as inputs (no information loss).
Pre-processing: Normalization, followed by a PCA.
・ Scenario 2b: 5 first PCA components
A Neural Network is trained using the 5 first PCA components (having the highest variance) as inputs.
Pre-processing: Normalization, followed by a PCA.
・ Scenario 3b: 5 PCA components selected using HVS
After training following Scenario 2a, the contributions of the inputs (the 18 PCA components) are measured using HVS technique. We select the 5 features having the highest contributions to put as inputs of a new neural network.
Pre-processing: Normalization, followed by a PCA.
・ Scenario 4a: 18 weighted PCA components
After training following Scenario 1a, the input feature contributions are measured using HVS technique. Then the normalized features are multiplied by the contributions following Equation 2. Then a PCA is applied to the 18 transformed features. Finally, the 18 PCA components are inputted to a new neural network.
Pre-processing: Normalization, followed by a weighting, followed by a PCA.
・ Scenario 4b: 5 first weighted PCA components
Following the same pre-processing steps of Scenario 4a, instead of keeping all 18 PCA components, only the 5 first PCA components (having the highest variance) are inputted to the neural network.
Pre-processing: Normalization, followed by a weighting, followed by a PCA.
・ Scenario 5a: PLS regression with 18 components
Pre-processing: Normalization only.
・ Scenario 5b: PLS regression with 5 components
Pre-processing: Normalization only.
Finally, scenarios 1c, 2c, 3c, 4c, 5c are identical to 1b, 2b, 3b, 4b, 5b, respectively, but with 3 features instead of 5.
5. Results
The experiments were conducted on a laptop with Intel core i7-3630QM processor (2.4 Ghz), 16 GB RAM. The software used is Matlab (R2012a) Neural Networks Toolbox.
Table 1 shows the classification performance (in terms of accuracy, false positive and false negative rates: FPR and FNR) on the testing database, and execution time (for training and test) for each tested scenario, which includes the pre-processing phase execution time. We can single out the following observations:
Table 1. Classification performance and execution time for each tested scenario.
- We notice that the number of hidden neurons in the neural network classifier has a direct incidence on the execution time.
- Scenario 1b (5 features selected by HVS) gives the best performance for a reduced feature set, according to all criteria (accuracy, FPR, FNR, and testing execution time), except for the learning time, which is not a critical criterion, since the learning process is made off-line once for all. Compared to scenario 1a (complete feature set), the reduction of the number of features by 72% (from 18 to 5) yields a decrease in accuracy by only 0.2% (from 0.9847 to 0.9828). This good performance may be explained by the coherence of the two phases (feature selection and classification both based on neural networks). The figures of scenario 1c show that an acceptable performance is kept even with only input features. Scenario 2c slightly outperforms it, however, in accuracy, FPR and execution time.
- All scenarios present a higher FPR than the FNR. This is the case of most anomaly-based detectors. Nevertheless, the ratio between FPR and FNR can be modified by changing the threshold used for the post-processing discretization.
- In terms of execution time, during the testing phase, the best scenarios are 1b (5 features selected by HVS), 1c (3 features selected by HVS) and 5b (PLS with 5 components). In all cases, the reduction of the input space markedly reduces the testing execution time (from 17%, for scenario 3b compared to 2a, up to 61%, for scenario 1b compared to 1a).
- Scenario 4c presents a high degradation of the classification performance, compared to 4a and 4b. It means that the weighted PCA technique, as described above, is sensitive to the number of retained components.
- PLS regression is a completely deterministic procedure, while the training procedure of NN needs a random initialisation of weights, and may need several runs to minimize the risk of getting a local optimal. Nevertheless, when applied during the testing phase, a trained NN becomes also a deterministic function (giving always the same output for a given output).
6. Related Works
There exist other feature selection methods that also based on neural networks, which are theoretically described in [10] . Nevertheless, to the best of our knowledge, none of these techniques has been yet applied to network features for solving the intrusion detection problem. We should consider and compare these techniques to the HVS method in future works. We need to thoroughly compare the HVS method to other feature selection methods, such as SVDF-based method or information gain-based method proposed by [11] .
Besides, several recent papers presented various feature selection techniques applied to network features. [12] proposed a hybrid approach combining the information gain ratio (IGR) and the k-means classifier. While [13] proposed a feature selection method based on Rough Sets, improved Genetic Algorithms and clustering. Then, they used the SVM classifier for performance evaluation on the KDD database. [14] proposed a clustering-based classifier selection method. This method selects the best classifier on similar clusters, compares it with the best classifier on the nearest cluster and then chooses the better one to make the system decision. It showed better results than the Clustering and Selection (CS) method. [15] constructed binary classifiers at local sensors to distinguish each class from the remaining classes. The authors used both a synthetic and the KDD99 datasets to confirm the improved performance of the pairwise feature subset selection algorithm for multiclass classification problems. [16] applied Artificial Bee Colony algorithm (ABC) to determine free parameters of support vector machine (SVM) and to achieve the optimum feature selection for IDSs. Reference [17] proposed a feature selection approach based on Bayesian Network classifier. The authors compared the performance of the proposed approach with other commonly used feature selection methods, and they demonstrated through empirical results that features selected by their approach have decreased the time to detect attacks and increased the classification accuracy as well as the true positive rates significantly. In a comparative study, [18] applied various types of classification techniques on NSL-KDD data, both for the two class problem as binary classification (normal and attack), and for a five class problem as multiclass classification. Then they applied feature selection techniques on random forest tree model, which was found to be the best model in both problems. The model produced the highest accuracy with 15 features in case of binary classification. Most of these works used KDD or NSL-KDD benchmark dataset. None of them used the more recent Kyoto 2006+ realistic dataset, as we did in this work.
On the other hand, various techniques in the literature are called “weighted PCA”, including weighting the original features before applying PCA, like we did in this paper, but also weighting the observations [19] , or using a weighted sum of the first k principal components of interest [20] .
7. Conclusion
In this paper, we have tested various feature selection and feature reduction scenarios, for the aim of classification of network traffic, using Kyoto 2006+ realistic dataset. We have measured the influence of reducing the number of features on the classification performance and the execution time. Among the tested scenarios, the HVS feature selection and the traditional PCA are revealed to be the most appealing, with an advantage of consistence and interpretability for the HVS feature, since the same learning algorithm (NN) is used for feature selection and for classification, and given the fact that PCA suffers from a lack of interpretability of the principal components since they are linear combinations of the original features, and generally do not have any physical meaning, especially when large numbers of features are involved. In future work, we will consider testing these different scenarios on other network datasets, such as DARPA and ISCX, to assess the consistency of our comparative study.
References
- Song, J., Takakura, H., Okabe, Y., Eto, M., Inoue, D. and Nakao, K. (2011) Statistical Analysis of Honeypot Data and Building of Kyoto 2006+ Dataset for NIDS Evaluation. Proceedings of the 1st Workshop on Building Analysis Datasets and Gathering Experience Returns for Security, Salzburg, 10-13 April 2011, 29-36. http://dx.doi.org/10.1145/1978672.1978676
- MIT Lincoln Lab., Information Systems Technology Group (1998) The 1998 Intrusion Detection Off-Line Evaluation Plan. http://www.ll.mit.edu/ideval/files/id98-eval-ll.txt
- Abdi, H. and Williams, L.J. (2010) Principal Component Analysis. Wiley Interdisciplinary Reviews: Computational Statistics, 2, 433-459. http://dx.doi.org/10.1002/wics.101
- Hornik, K., Stinchcombe, M. and White, H. (1989) Multilayer Feedforward Networks Are Universal Approximators. Neural Networks, 2, 359-366. http://dx.doi.org/10.1016/0893-6080(89)90020-8
- Huang, G.B., Chen, Y.Q. and Babri, H.A. (2000) Classification Ability of Single Hidden Layer Feedforward Neural Networks. IEEE Transactions on Neural Networks, 11, 799-801. http://dx.doi.org/10.1109/72.846750
- Wong, P.M., Gedeon, T.D. and Taggart, I.J. (1995) An Improved Technique in Porosity Prediction: A Neural Network Approach. IEEE Transactions on Geoscience and Remote Sensing, 33, 971-980. http://dx.doi.org/10.1109/36.406683
- Yacoub, M. and Bennani, Y. (1997) HVS: A Heuristic for Variable Selection in Multilayer Artificial Neural Network Classifier. Intelligent Engineering Systems through Artificial Neural Networks, St. Louis, January 1997, 527-532.
- Wold, H. (1975) Soft Modeling by Latent Variables: The Nonlinear Iterative Partial Least Squares Approach. Perspectives in Probability and Statistics, Papers in Honour of MS Bartlett, 520-540.
- Haenlein, M. and Kaplan, A.M. (2004) A Beginner’s Guide to Partial Least Squares Analysis. Understanding Statistics, 3, 283-297. http://dx.doi.org/10.1207/s15328031us0304_4
- Leray, P. and Gallinari, P. (1999) Feature Selection with Neural Networks. Behaviormetrika, 26, 145-166.
- Kayacik, H.G., Zincir-Heywood, A.N. and Heywood, M.I. (2005) Selecting Features for Intrusion Detection: A Feature Relevance Analysis on KDD 99 Intrusion Detection Datasets. Proceedings of the 3rd Annual Conference on Privacy, Security and Trust, 12-14 October 2005, 85-89.
- Araújo, N., de Oliveira, R., Ferreira, E.-W., Shinoda, A.A. and Bhargava, B. (2010) Identifying Important Characteristics in the KDD99 Intrusion Detection Dataset by Feature Selection Using a Hybrid Approach. 2010 IEEE 17th International Conference on Telecommunications (ICT), Doha, 4-7 April 2010, 552-558. http://dx.doi.org/10.1109/ICTEL.2010.5478852
- Guo, Y., Wang, B., Zhao, X., Xie, X., Lin, L. and Zhou, Q. (2010) Feature Selection Based on Rough Set and Modified Genetic Algorithm for Intrusion Detection. 2010 5th International Conference on Computer Science and Education (ICCSE), Hefei, 24-27 August 2010, 1441-1446. http://dx.doi.org/10.1109/ICCSE.2010.5593765
- Mi, A.Z. and Hai, L.P. (2010) A Clustering-Based Classifier Selection Method for Network Intrusion Detection. 2010 5th International Conference on Computer Science and Education (ICCSE), Hefei, 24-27 August 2010,1001-1004. http://dx.doi.org/10.1109/ICCSE.2010.5593398
- Nguyen, H.D. and Cheng, Q. (2011) An Efficient Feature Selection Method for Distributed Cyber Attack Detection and Classification. 2011 45th Annual Conference on Information Sciences and Systems (CISS), Baltimore, 23-25 March 2011, 1-6. http://dx.doi.org/10.1109/CISS.2011.5766239
- Wang, J., Li, T.H. and Ren, R.R. (2010) A Real Time IDSs Based on Artificial Bee Colony-Support Vector Machine Algorithm. 2010 3rd International Workshop on Advanced Computational Intelligence (IWACI), Suzhou, 25-27 August 2010, 91-96.
- Zhang, F.L. and Wang, D. (2013) An Effective Feature Selection Approach for Network Intrusion Detection. 2013 IEEE 8th International Conference on Networking, Architecture and Storage (NAS), Xi’an, 17-19 July 2013, 307-311. http://dx.doi.org/10.1109/NAS.2013.49
- Hota, H.S. and Shrivas, A.K. (2014) Data Mining Approach for Developing Various Models Based on Types of Attack and Feature Selection as Intrusion Detection Systems (IDS). In: Mohapatra, D.P. and Patnaik, S., Eds., Intelligent Computing, Networking, and Informatics, Springer India, New Delhi, 845-851. http://dx.doi.org/10.1007/978-81-322-1665-0_85
- Jackson, J.E. (2005) A User’s Guide to Principal Components, Volume 587. John Wiley & Sons, Hoboken.
- Kim, S.B. and Rattakorn, P. (2011) Unsupervised Feature Selection Using Weighted Principal Components. Expert Systems with Applications, 38, 5704-5710. http://dx.doi.org/10.1016/j.eswa.2010.10.063
Annex I: KYOTO Dataset Input Features
1. Duration: the length (seconds) of the connection.
2. Service: the connection’s service type, e.g., http, telnet.
3. Source bytes: the number of data bytes sent by the source IP address.
4. Destination bytes: the number of data bytes sent by the destination IP address.
5. Count: the number of connections whose source IP address and destination IP address are the same as those of the current connection in the past two seconds.
6. Same srv rate: % of connections to the same service in Count feature.
7. Serror rate: % of connections that have “SYN” errors in Count feature.
8. Srv serror rate: % of connections that have “SYN” errors in Srv count (the number of connections whose service type is the same to that of the current connection in the past two seconds) feature.
9. Dst host count: among the past 100 connections whose destination IP address is the same as that of the current connection, the number of connections whose source IP address is also the same as that of the current connection.
10. Dst host srv count: among the past 100 connections whose destination IP address is the same as that of the current connection, the number of connections whose service type is also the same as that of the current con- nection.
11. Dst host same src port rate: % of connections whose source port is the same as that of the current con- nection in Dst host count feature.
12. Dst host serror rate: % of connections that have “SYN” errors in Dst host count feature.
13. Dst host srvs error rate: % of connections that “SYN” errors in Dst host srv count feature.
14. Flag: the state of the connection at the time the connection was written.
15. Source port number: indicates the source port number used in the session.
16. Destination port number: indicates the destination port number used in the session.
17. Start time: indicates when the session was started.
18. Duration: indicates how long the session was being established.


