Open Journal of Modelling and Simulation
Vol.05 No.03(2017), Article ID:77111,5 pages
10.4236/ojmsi.2017.53012
Spacetime from Zitterbewegung
Mohamed S. El Naschie
Dept. of Physics, Faculty of Science, University of Alexandria, Alexandria, Egypt

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 13, 2017; Accepted: June 20, 2017; Published: June 23, 2017
ABSTRACT
Quantum particles are assumed to have a path constituting a random fluctuation super imposed on a classical one resulting in a golden mean spiral propagating in spacetime. Consequently, the dimension of the path of the quantum particle is given by one plus the random Cantor set Zitterbewegung, i.e. 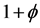 where
where 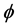 is the golden mean Hausdorff dimension of a random Cantor set. Proceeding in this way, we can derive the basic topological invariants of the corresponding spacetime which turned out to be that of E-infinity spacetime
is the golden mean Hausdorff dimension of a random Cantor set. Proceeding in this way, we can derive the basic topological invariants of the corresponding spacetime which turned out to be that of E-infinity spacetime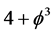 as well as a fractal Witten’s M-theory
as well as a fractal Witten’s M-theory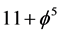 . Setting
. Setting  and
and 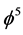 equal zero, we retrieve Einstein’s spacetime and Witten’s M-theory spacetime respectively where
equal zero, we retrieve Einstein’s spacetime and Witten’s M-theory spacetime respectively where 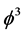 is the latent Casimir topological pressure of spacetime and
is the latent Casimir topological pressure of spacetime and 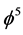 is Hardy’s quantum entanglement of the same.
is Hardy’s quantum entanglement of the same.
Keywords:
Zitterbewegung, E-Infinity Theory, Quantum Physics, Einstein Spacetime, Fractal Spacetime, Witten Spacetime, ‘tHooft Cellular Automaton

1. Introduction
There is an excellent model for Zitterbewegung due to Arend Niehaus, University of Utrecht Physics Professor [1] . This model interpreted in the right way leads to a general theory which goes a long way towards a quantum physics without quantum mechanics or at least without the orthodox form of quantum mechanics [2] [3] [4] . The present short note builds upon this work and shows that by means of minimal number theoretical adjustment, Niehaus’s model leads to the basic conclusions of E-infinity Cantorian-fractal spacetime theory [5] and related models [5] - [20] . In particular, we can derive the exact Hausdorff dimension of spacetime and show how it arises naturally from the basic Zitterbewegung model mentioned above [1] . Even more importantly, the present note restores the meaning of a path to quantum physics once we extend the meaning beyond that of a one dimensional line of a propagating point particle [5] [6] as will be shown in what follows.
2. Analysis
As mentioned in the present Introduction earlier on, the basic idea of the Niehaus Zitterbewegung model [1] is to replace the ordinary path of a classical particle 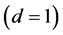 by a spiralling line representing a path and a spin simultaneously. Therefore, we could say with reasonable justification that the model is a second generation development of the area-like quantum particle path introduced probably for the first time by Abbot and Wise [5] [6] and subsequently integrated into the fractal spacetime theory of G. Ord and sometime later, L. Nottale [5] and later still by the present author in his E-infinity Cantorian spacetime theory [5] . However there is a crucial difference between the Cantorian area-like path proposal [5] and all other proposals, namely that in E-infinity theory, the “quantum” path of the “quantum” particle is described not by a single Hausdorff or topological dimension, but rather with two inter-dependent dimensions [5] . More precisely in E-infinity theory we use both dimensions simultaneously, namely the topological dimension
by a spiralling line representing a path and a spin simultaneously. Therefore, we could say with reasonable justification that the model is a second generation development of the area-like quantum particle path introduced probably for the first time by Abbot and Wise [5] [6] and subsequently integrated into the fractal spacetime theory of G. Ord and sometime later, L. Nottale [5] and later still by the present author in his E-infinity Cantorian spacetime theory [5] . However there is a crucial difference between the Cantorian area-like path proposal [5] and all other proposals, namely that in E-infinity theory, the “quantum” path of the “quantum” particle is described not by a single Hausdorff or topological dimension, but rather with two inter-dependent dimensions [5] . More precisely in E-infinity theory we use both dimensions simultaneously, namely the topological dimension 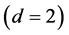 as well as the corresponding Hausdorff dimension exactly as in the continuous geometry model of von Neumann-Connes as applied to Penrose fractal tiling universe [5] - [12] which re- presents more over a generic case of a specific noncommutative geometry [5] . It is easily shown using the corresponding dimensional function of von Neumann- Connes [5] or the equivalent bijection formula of E-infinity that for
as well as the corresponding Hausdorff dimension exactly as in the continuous geometry model of von Neumann-Connes as applied to Penrose fractal tiling universe [5] - [12] which re- presents more over a generic case of a specific noncommutative geometry [5] . It is easily shown using the corresponding dimensional function of von Neumann- Connes [5] or the equivalent bijection formula of E-infinity that for 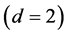 topological dimension of a “quantum” particle, the Hausdorff dimension is
topological dimension of a “quantum” particle, the Hausdorff dimension is 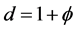 where
where 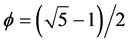 is the golden mean, also used extensively in [7] . In the notation of E-infinity this means [5] [8]
is the golden mean, also used extensively in [7] . In the notation of E-infinity this means [5] [8]
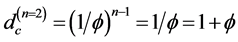 (1)
(1)
Now starting from Newtonian three dimensional classical space, we see that the corresponding dimension must be the triadic intersection given by
 (2)
(2)
This is clearly the Hausdorff dimension of a 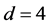 Einstein spacetime as given by the bijection formula [5]
Einstein spacetime as given by the bijection formula [5]
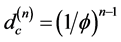 (3)
(3)
so that 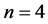 leads to [5] [8]
leads to [5] [8]

The connection to Zitterbewegung of the Niehaus model and the associated theory [1] is as follows.
It is a well known mathematical-geometrical fact that except for the straight line and the perfect circle, only the logarithmic spiral is infinitely self similar homogeneous. In addition the spiral in two dimensions arises from the construction of a random one dimensional Cantor dust (set) with uniform distribution [12] . The Hausdorff dimension of such a set, as shown long ago in a work by D. Mauldin in a paper dedicated to S. Ulam, is given by the golden mean 

Before concluding this section let us show using the above result a remarkable derivation connecting superstrings 




where 





with which we conclude this compressed, very short analysis. For in depth study of the ideas and theories discussed here, the reader is directed to Refs. [9] - [11] and as far as E-infinity theory is concerned, Refs. [12] - [20] are quite valuable.
3. Conclusions
The effort of what might be called the Utrecht Dutch School of G. ‘tHooft in inventing or discovering a quantum physics without the unintuitive and/or at least classically paradoxical orthodox quantum mechanics seems to have some considerable success by the non-mainstream efforts of people like Gerard ‘tHooft himself [9] and recently Niehaus Zitterbewegung theory [1] . These efforts are by no means confined to the work carried out in Holland [9] and there are various schools all over the world seriously engaged in the dream of restoring at least partially, some of our Newtonian classical intuition and common sense to modern quantum physics and cosmology, for instance by S. Weinberg [10] [11] . We hasten to say that it would be philosophically misguided to think that matrix quantum mechanics, Schrödinger and Dirac’s equations, let alone the marvellous quantum field theory did not bring to us a considerable understanding of nature or that it was all a historical accident, not more. It is just the contrary because it was these methods and theories [11] which made an almost exact prediction but failed to satisfy our deep seated human need or urge for understanding which compelled us to travel all possible roads and to climb all possible mathematical and theoretical physics mountains [11] [12] to see the horizon at infinity [11] . It is may be as expressed by Niels Bohr, thegreat Dane in astonishingly eloquent German [12] .
“Nur in der fuller Liegt die Klarkeit”, i.e. only in the abundance lies clarity.
This does not only apply to the physical phenomena but also to the mathematical models and theories which we apply [12] .
Cite this paper
El Naschie, M.S. (2017) Spacetime from Zitterbewegung. Open Journal of Modelling and Simula- tion, 5, 169-173. https://doi.org/10.4236/ojmsi.2017.53012
References
- 1. Niehaus, A. (2017) Zitterbewegung and the Electron. Journal of Modern Physics, 8, 511-521.
https://doi.org/10.4236/jmp.2017.84033 - 2. El Naschie, M.S. (2007) On Gauge Invariance, Dissipative Quantum Mechanics and Self Adjoint Sets. Chaos, Solitons & Fractals, 32, 271-273.
- 3. El Naschie, M.S. (1995) A Note on Quantum Mechanics, Diffusional Interference and Information. Chaos, Solitons & Fractals, 5, 881-884.
- 4. El Naschie, M.S. (2007) Deterministic Quantum Mechanics versus Classical Mechanical Indeterminism and Nonlinear Dynamics. American Institute of Physics, AIP Conference Proceedings No. 905, May 2007, New York, 56-66.
- 5. El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236.
- 6. Abbot, L.F. and Wise, M.B. (1981) Dimensions of a Quantum Path. American Journal of Physics, 49, 37-39.
https://doi.org/10.1119/1.12657 - 7. Jan, C.A. (2013) Boeyens: The Chemistry of Matter Waves. Springer, Berlin, Germany.
- 8. El Naschie, M.S. (2016) On a Fractal Version of Witten’s M-theory. Journal of Astronomy & Astrophysics, 6, 135-144.
- 9. ‘tHooft, G. (2016) The Cellular Automaton Interpretation of Quantum Mechanics. Springer Open (Springer International Publishing, Germany), Berlin.
https://doi.org/10.1007/978-3-319-41285-6 - 10. Weinberg, S. (2014) Quantum Mechanics without State Vectors.
http://arxiv.org/pdf/1405.3483v1.pdf - 11. Weinberg, S. (2015) To Explain The World: The Discovery of Modern Science. Harper, New York, USA.
- 12. El Naschie, M.S. (2016) Einstein’s Dark Energy via Similarity Equivalence, ‘tHooft Dimensional Regularization and Lie Symmetry Groups. International Journal of Astronomy & Astrophysics, 6, 56-81.
https://doi.org/10.4236/ijaa.2016.61005 - 13. El Naschie, M.S. (2017) The Looped Light of the Triple-Slit Real Experiment as a Confirmation for the Extra Dimensions of Quantum Spacetime and the Reality of Dark Energy. Optical and Photonic Journal, 7, 19-26.
https://doi.org/10.4236/opj.2017.72003 - 14. El Naschie, M.S. (2017) Looped Light on Dark Energy. Journal of Quantum Information Science, 7, 43-47.
https://doi.org/10.4236/jqis.2017.72004 - 15. El Naschie, M.S. (2017) The Quantum Triple-Slit Experiment and Dark Energy. Open Journal of Microphysics, 7, 31-35.
https://doi.org/10.4236/ojm.2017.72002 - 16. El Naschie, M.S. (2017) Quantum Disentanglement as the Physics Behind Dark Energy. Open Journal of Microphysics, 7, 1-27.
https://doi.org/10.4236/ojm.2017.71001 - 17. El Naschie, M.S. (2017) Kähler Dark Matter, Dark Energy, Cosmic Density and Their Coupling. Journal of Modern Physics, 7, 1953-1962.
- 18. El Naschie, M.S. (2016) Completing Einstein’s Spacetime. Journal of Modern Physics, 7, 1972-1994.
https://doi.org/10.4236/jmp.2016.715175 - 19. El Naschie, M.S. (2016) High Energy Physics and Cosmology as Computation. American Journal of Computational Mathematics, 6, 185-199.
https://doi.org/10.4236/ajcm.2016.63020 - 20. El Naschie, M.S. (2005) On a Fuzzy Kähler-Like Manifold Which Is Consistent With The Two Slit Experiment. International Journal of Nonlinear Sciences and Numerical Simulation, 6, 95-98.
https://doi.org/10.1515/IJNSNS.2005.6.2.95

