Open Journal of Modelling and Simulation
Vol.05 No.01(2017), Article ID:72667,12 pages
10.4236/ojmsi.2017.51001
When Do Adobe Bricks Collapse under Compressive Forces: A Simulation Approach
Markus Rauchecker1, Manfred Kühleitner2*, Norbert Brunner2, Klaus Scheicher2, Johannes Tintner3, Maximilian Roth4, Karin Wriessnig4
1BOKU, Institut für Geotechnik, Wien, Austria
2BOKU, Institut für Mathematik, Wien, Austria
3BOKU, Institut für Holztechnologie und Nachwachsende Rohstoffe, Tulln an der Donau, Austria
4BOKU, Institut für Angewandte Geologie, Wien, Austria

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 24, 2016; Accepted: December 6, 2016; Published: December 9, 2016
ABSTRACT
The collapse of adobe bricks under compressive forces and exposure to water has a duration of several minutes, with only minor displacements before and after the collapse, whence a conceptual question arises: When does the collapse start and when does it end? The paper compares several mathematical models for the description of the fracture process from displacement data. It recommends the use of linear splines to identify the beginning and end of the collapse phase of adobe bricks.
Keywords:
Adobe Brick, Compressive Strength, Low Pass Filter, Least Squares Fit, Linear Splines, Pattern Recognition

1. Introduction
Traditional adobe architecture, using unburnt clay bricks, is still common in many parts of the world [1] [2] , and loam (a mixture of sand, silt and clay; other compositions of materials have been used, too), has been used as construction material since ancient times [3] .
Using adobe bricks for construction is ecologically and economically sustainable [4] . Amongst the main benefits are the high availability of loam and therefore low efforts to transport it. The energy demand for processing of building material is low [5] : Unfired bricks take 5 to 10 kWh/m3, while fired bricks require about 1300 kWh/m3. Unfired bricks can be recycled very easily and there is no need for landfill sites. The energy demand for recycling is low, because it is only necessary to mix with water and form new bricks. Further, adobe bricks are a physically sound construction material with desirable thermal properties [6] . If constructed properly, adobe houses may withstand major earthquakes [7] .
As to disadvantages, adobe walls must be protected from direct contact with water (Figure 1), as otherwise a loss of stability of the construction may occur [8] . Unexpected incidents, such as floods, heavy rainfall, high level of underground water, bursting of pipes or other technical reasons may expose adobe walls to water for a longer period. In order to develop material compositions that are more resistant to humidity, standardized testing is needed. The purpose of this paper is the investigation of the combined resistance of adobe bricks against water and pressure by measurements of adobe bricks placed on a humid base. The paper, thereby, defines a standardized method to determine, when the break of such bricks starts and ends (collapse phase). The later the break starts, the more resistant to water is the material, and the slower it breaks (duration of the collapse phase), the higher are the chances to leave a crumbling building.
2. Problem
There is a rich literature on testing the compressive strength of dry adobe bricks. In most cases the purpose is the optimization of the material mix, e.g. [9] [10] . There are various technical standards for such tests, e.g. a regional standard for Africa [11] or a national standard [12] in Spain, used also in Latin America. Thereby, an adobe brick is placed into a compression load testing machine and subjected to successively increasing load; the machine stops automatically, when the brick breaks. In the context of earthquake security, shaking tests of adobe brick walls were developed [13] . Compression load testing machines were also applied to test the strength of wet adobe bricks that prior to the measurement had absorbed moisture for several days [14] . As wet adobe bricks were breaking so slowly, the break point load could not be detected automatically; it was determined from an optical inspection [15] .
Such experiments could provide only indirect information about how long an adobe wall might withstand the contact with water. In order to approach this question directly, an experimental setup was designed, that enables the measurement for a period of up to several days of the deformation of an adobe brick under constant pressure, while at the same time the water content was increasing. This simulated an adobe brick in a wall exposed to moisture from a wet underground.
Multiple experiments [5] verified that the typical pattern of the fracture of such
Figure 1. Wet adobe brick after fracture.
treated adobe bricks was in three phases. Initial resistance phase with minor displacements for a day or more, collapse within several minutes and final phase with only minor displacements for the crushed brick. Thus, the fracture process may be characterized by the points of time, t0 and t1, when the collapse begins and ends. The goal of the paper is the proposal of a computational method to automatically identify t0 and t1 from the displacement data. To this end, the paper compares several mathematical models for describing the fracture process. (Appendix II summarizes the Mathematica codes for these models.) Basically, the problem of this paper is a conceptual one of defining the collapse phase by a standardized method.
3. Materials and Methods
The experimental setting of this paper (Figure 2) differs fundamentally from the above mentioned standardized procedures, as the aim was to test, for how long an adobe wall could withstand contact with water. Therefore, the compressive load was kept constant, while the brick was exposed to water, and the break point time was sought for, not a break point load.
An adobe brick was placed on a saturated filter layer of fine, clean sand (height 1.5 cm). The increasing saturation of the brick resulted from the capillary rise through the bedding. Thus, the water level did not reach the brick directly, but by contact to the bottom of the brick. The experiment used adobe bricks of size 24.5 × 12 × 6 cm, with a dry density of 2100 kg/m³, produced by an extrusion process at the brickyard Nicoloso (Pottenbrunn/Austria). Appendix I provides more information about the material characteristics. A load of F = 1.8 kN, comparable to the compressive force to the lowest brick of an adobe wall of 3 m height, was applied vertically to the surface of the adobe brick by a lever arm that was flexibly jointed to an aluminum plate (25 × 13 × 2.5 cm) on top of the brick to get a uniform load distribution of initially 6.1 N/cm2 for the brick and 5.5 N/cm2, when the plate dipped into the crumbled material (Figure 1). The fracture process of the brick was measured by a displacement transducer with a precision of 0.05 mm. To protect the transducer, the maximal displacement was limited to 25 mm. The measurement interval was 10 seconds, but experience showed that increasing this interval to 30 seconds still resulted in a satisfactory resolution of the data. The time
Figure 2. Schematic illustration of the experimental assembly.
Figure 3. Data of this paper (displacement over time of an adobe brick).
span for these displacement measurements was up to two days. Displacement data were recorded in a spreadsheet (Microsoft EXCEL 2016). As a first reduction of complexity, for each brick only the average displacements per minute (obtained from a pivot table) were further analyzed. Thus, for time t this paper denotes by d(t) the measured average displacement of the considered brick. The experiment started at time t = 0 and the data for Figure 3 recorded the vertical displacements over 2350 minutes (duration tmax = 1.631 days = 39¼ hours, maximal displacement dmax = 22.382 mm).
The authors tested only one type of adobe, characterized in Appendix I, as the purpose of the paper is the proof of principle for one type of materials. The paper does not aim at the optimization of materials. Rather, given displacement data as in Figure 3, the paper asks, when did the collapse of the brick occur? It could be roughly identified from an optical inspection of Figure 3, indicating a steep slope at ca. t = 1.3 days. More difficult is the determination of the time t0, when the collapse began, and of t1, when the collapse ended. The paper compares four models for describing the fracture process and defining t0 and t1. These models do not aim at an explanation of the physical process of fracture, but at a description of the displacement data that allows for the identification of collapse phase. Intuitively, at time t0 the brick was irreversibly damaged (break point time) and at time t1 it was crumbling. However, this paper does not aim at verifying this intuition. The methodology underlying these models is explained briefly together with the results.
4. Results of the Models
4.1. Pattern Recognition
A first attempt towards the description of the data used methods of pattern recognition, as illustrated by the coloring in Figure 3: Black dots identify data points corresponding to the collapse phase, green dots indicate the first and the last phase. This resulted in the estimate t0 = 1.225 days (with 1.29 mm displacement) and t1 = 1.294 days (with 9.88 mm displacement). However, the black cluster corresponding to collapse missed the second half of this phase.
As to the method of pattern recognition, the paper used cluster analysis to identify three groups of data points (corresponding to the three phases) with a small distance amongst them. In order to improve the clustering, a modification of two-dimensional Euclidean distance was used, defining as nil the distance between data points, whose displacements differed by less than a threshold of 1.0 mm. The local optimization algorithm of [16] then automatically detected the plotted clustering, using Mathematica software.
This method was not fully automatic, as pattern recognition generally is rather a learning technique. Thus, the distance function had to be modified, using a threshold that was adapted to the data by trial-and-error. The output was also dependent on the selected algorithm; e.g. hierarchical agglomerative clustering did produce inferior results.
4.2. Data Smoothing
As indicated by Figure 3, collapse is characterized by a rapid increase of the measured displacements. This suggests that the analysis of the speed of fracture (differences of successive displacements) might inform about the collapse. A direct visual inspection of the differences (green dots) in Figure 4 indicates random fluctuations that may hide, when the collapse actually begins or ends. However, a smoothing of the data (black curve) identified an initial phase of stability followed by high differences in the filtered data in the neighborhood of ca. 1865 minutes (maximum measured speed of collapse: 3.36 mm/min) and another final phase of stability. More specifically, the 5% largest difference of filtered data occurred between minutes 1807 and 1923, resulting in the estimates t0 = 1.255 days and t1 = 1.335 days.
As to the method of data smoothing, the paper used a low-pass filter to eliminate high-frequency fluctuations. It passes signals with a frequency lower than a chosen cutoff frequency. The computation was done in Mathematica.
This method was not fully automatic, as both the cutoff frequency (here: 0.01) and the threshold for the quantile (here 95%) was manually adjusted by trial-and-error. Further, the threshold for the quantile could not be defined without knowledge of the yet unknown duration of the collapse. For example, defining the collapse from the 95% quantile assumes that 5% of the data points describe this phase. For the present data this in turn corresponded to a time span of 117 minutes, which overestimated the duration of collapse.
Figure 4. Speed of fracture over time: unfiltered (green dots) and filtered (black line).
Also the cutoff frequency should neither be too small nor too large. It should not be too small, as the overall shape of the original data should be retained (a smaller cutoff frequency estimates lower t0 and higher t1). It should not be too high, either, as then also in other regions the differences might exceed the given quantile. (Example: For a cutoff frequency of 0.1 the differences exceed the 95% quantile between minutes 112 to 150, 270 to 283 and 1840 to 1905, whereby only the latter interval corresponded to the collapse.) This reasoning applies in particular to the unfiltered data (a cutoff frequency of 2p defines an all-pass filter).
4.3. Jump Model Approximation
An elementary approach identified the three phases of fracture from an approximation by a linearized jump function (Figure 5, dashed red curve). The phases divide the timeline into three intervals i = 1, 2, 3 between t = 0 and t0, between t0 and t1 and between t1 and infinity. For the present data this resulted in the estimates t0 = 1.29 days and t1 = 1.299 days.
As to the method, the following model was used to approximate the fracture process: No displacement till t0, maximal displacement after t1 and linear in between. The parameters t0 and t1 of this model were determined by using the method of least squares to find a best fit of the jump model to the data.
However, this approach turned out to be insofar not satisfactory, as the fit to the data of the initial resistance phase was poor.
4.4. Linear Spline Model Approximation
This approach improves the simple jump model insofar, as it describes the displacement by a linear spline function (Figure 5, black curve). For the present data this resulted in the estimates t0 = 1.292 days (actual displacement 3.50 mm, model 1.84 mm) and t1 = 1.298 days (actual displacement 20.39 mm, model 21.82 mm). These estimates were insofar satisfactory, as the actual deformations were within 4 mm of the minimal respectively maximal level, whence in the time span between t0 and t1 most of the deformation (16.89 mm = 75% of the measured maximal displacement) occurred.
As to the method, the following model of the fracture process was used: Again, three intervals i = 1, 2, 3 between t = 0 and t0, between t0 and t1 and between t1 and infinity were considered and on each interval the fracture was approximated by a linear function
Figure 5. Displacement data (green), jump model (dashed red), and spline model (black).
di(t) of time, formula (1). These linear functions are not the regression lines, but linear splines, because the model assumes in addition that the displacement should be continuous, formula (2), which says d1(t0) = d2(t0) and d2(t1) = d3(t1). A further reduction of the number of parameters could be achieved by formula (3), stipulating that the linear spline originates from 0 and ends with the maximal measured displacement dmax; summarizing:
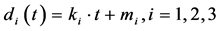 (1)
(1)
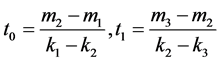 (2)
(2)
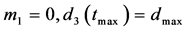 (3)
(3)
The goal was to find the best fit of this model to the measured displacement data d(t), using the method of least squares. The parameters of the model were ki and mi, from which ti were computed by formula (2).
In comparison to the jump model, the better fit of this model to the observed displacements made it superior. For the present data this could also be verified in terms of the Akaike information criterion for model selection [17] . As to possible limitations of this method, the approximation to the actual displacements was worst close to t0 and t1 (Figure 5). Thus, different methods need to be developed, if one aims at measuring the maximal reversible displacement (elasticity) prior to the begin of collapse.
5. Discussion and Conclusion
As is well-known (references cited above) the material characteristics, e.g. grain size distribution or use of additives, strongly influences the stability of adobe bricks. A new experimental setting was designed to test, for how long an adobe wall could withstand contact with water, asking for the break point time under constant pressure of an adobe brick, which absorbs water by capillarity. In order to optimize the material mix under the aspect of a combined resistance to pressure and water, large test series are needed, whence the identification of the collapse phase needs to be automatized. Thus, in order to compare and optimize different materials, the break point time needs to be determined by a standardized method.
While it was easy to derive a rough estimate from a visual inspection of plotting displacement data, a more accurate definition of the break point time turned out to be conceptually demanding, owing to the slow fracture process. Therefore, instead of characterizing the fracture process by one break point time, the paper proposes to determine the beginning and end of the collapse phase. Of the four models considered for this purpose, the linear spline approximation based on Equations ((1) to (3)) turned out to be the most viable approach, suitable for automatization.
Further, the authors considered that the experimental setting and the subsequent data analysis (computational identification of the collapse phase) should be simple and inexpensive. For adobe bricks are mainly used in developing countries. There the optimization of materials by using locally available additives needs to be done at the village level, where engineers may not have access to sophisticated machines or software. The present experimental setting (Figure 2) is a low cost design and therefore viable for developing countries. Also the linear spline approximation approach could be automatized in common spreadsheet programs, i.e. it does not require expensive software and it is therefore suitable for use in developing countries. For instance, working in Microsoft EXCEL, the SOLVER add-in can be used for determining parameters ki, mi from formula (1), where the sum of squares of the differences between the measured displacement and the displacements calculated from the linear spline model is minimal. The authors have prepared an EXCEL file (explained in Appendix III) and make it available online. Summarizing, the authors propose the linear spline approximation to describe the fracture process of adobe bricks in contact with water, as it is specifically adapted to the needs of users of adobe bricks in developing countries.
Cite this paper
Rauchecker, M., Kühleitner, M., Brunner, N., Scheicher, K., Tintner, J., Roth, M. and Wriessnig, K. (2017) When Do Adobe Bricks Collapse under Compressive Forces: A Simulation Approach. Open Journal of Modelling and Simulation, 5, 1-12. http://dx.doi.org/10.4236/ojmsi.2017.51001
References
- 1. Houben, H. and Guillaud, H. (2006) Traité de construction en terre. Paranthese, Marseille.
- 2. Mileto, C., Vegas, F., García Soriano, L. and Cristini, V. (2015) Vernacular Architecture: towards a Sustainable Future. Taylor & Francis, London.
- 3. Love, S. (2012) The Geoarchaeology of Mudbricks in Architecture: A Methodological Study from Catalhoyuk, Turkey. Geoarchaeology, 27, 140-156.
https://doi.org/10.1002/gea.21401 - 4. Berge, B. (2009) The Ecology of Building Materials. Architectural Press, Oxford, UK.
- 5. Roth, M. (2014) Einfluss unterschiedlicher Rohstoffe auf die Druckfestigkeit und das Verformungsverhalten von Lehmziegeln unter Wassereinfluss. Master Thesis, BOKU, Vienna.
- 6. Palme, M., Guerra, J. and Alfaro, S. (2014) Thermal Performance of Traditional and New Concept Houses in the Ancient Village of San Pedro De Atacama and Surroundings. Sustainability, 6, 3321-3337.
https://doi.org/10.3390/su6063321 - 7. Minke, G. and Schmidt, H.P. (2015) Building Earthquake Resistant Clay Houses. Ithaka- Journal for Biochar Materials, Ecosystems and Agriculture, 2015, 349-355, www.ithaka-journal.net/87
- 8. Reman, O. (2004) Increasing the Strength of Soil for Adobe Construction. Architectural Science Review, 47, 373-386.
https://doi.org/10.1080/00038628.2000.9697547 - 9. Millogo, Y., Aubert, J.-E., Hamard, E. and Morel, J.-C. (2015) How Properties of Kenaf Fibers from Burkina Faso Contribute to the Reinforcement of Earth Blocks. Materials, 8, 2332-2345.
https://doi.org/10.3390/ma8052332 - 10. Schicker, A. and Gier, S. (2009) Optimizing the Mechanical Strength of Adobe Bricks. Clay and Clay Minerals, 57, 494-501.
https://doi.org/10.1346/CCMN.2009.0570410 - 11. African Regional Organization of Standardization (1996). Compressed Earth Blocks, Standard for Classification of Material Identification Tests and Mechanical Tests. Standard ARS-683, Accra, Ghana.
- 12. AsociaciónEspañola de Normalización y Certificación (2008) Compressed Earth Blocks for Walls and Partitions. Definitions, Requirements and Test Methods. Standard UNE-41410, Madrid, Spain.
- 13. Samali, B., Dowling, D.M. and Li, J. (2008) Dynamic Testing and Analysis of Adobe- Mudbrick Structures. Australian Journal of Structural Engineering, 8, 63-75.
- 14. Vilane, B.R.T. (2010) Assessment of Stabilization of Adobes by Confined Compression Tests. Biosystems Engineering, 106, 551-558.
https://doi.org/10.1016/j.biosystemseng.2010.06.008 - 15. Jiménez Zomá, N.J., Guerro, L.F. and Jové, F. (2015) Methodology to Characterize the Use of Pine Needles in Adobes of Chipas, Mexico. In (, pp. 371-376).
- 16. Breiman, L., Friedman, J., Stone, C.J. and Olshen, R.A. (1984) Classification and Regression Trees. Chapman & Hall, New York.
- 17. Burnham, K.P. and Anderson, D.R. (2002) Model Selection and Multi-Model Inference: A Practical Information-Theoretic Approach. Springer Publ., Heidelberg.
Appendix I: Material Characteristics
In order to allow a comparison of the present data with literature data, the grain size distribution of the brick was determined with a combined wet sieving of the fraction > 40 μm and automatic sedimentation analysis with Sedi Graph III (Micromeritics).
An air-dried sample of 50 g was treated with 200 ml of 10% H2O2 for oxidation of organic components and proper dispersion. After ca. 24 h reaction time and removal of the remaining H2O2, the sample was treated with ultrasound and sieved with a set of 2000 μm, 630 μm, 200 μm, 63 μm and 20 μm sieves. The coarse fractions were dried at 105˚C, weighed, and measured in mass percent. The <20 μm portion was suspended in water, a representative portion was taken out, treated with 0.05% sodium polyphosphate and ultrasound, and analyzed in a sedigraph by X-ray, according to Stokes’ Law. From the cumulative curve of the sedigraph and the sieving data, the grain size distribution of the entire sample was calculated (see Figure 6).
Appendix II: Mathematica Codes
As some models used highly sophisticated tools, their code is summarized and annotated below, using Mathematica 11 software of Wolfram Research. It provides these tools in the form of a “black box”.
The following commands relate to certain characteristics of the data. Thereby, “full_data” was the original input, comprised of the pairs time (in days) and displacement (in mm), while “disp_data” retained the displacement information (per minute), only. Further, “tmax” was the duration tmax = 1.631 days of the measurements and “dismax” the maximal displacement (22.38 mm).
full_data = {{0, 0.025}, {0.000694444, 0.124}, …};
disp_data = Last[Transpose[full_data]];
{tmax = Max[First[Transpose[full_data]]],
dismax = Max[Last[Transpose[full_data]]]}
The following key commands were used for the pattern recognition. The first line
Figure 6. Cumulative grain size distribution.
defines the modified distance, the second line identifies the clusters, the third line plots them and the last line extracts the bounds t0 and t1 from the second cluster.
modifieddist[u_, v_] = If[Abs[Last[u] -Last[v]] < 1.0, 0, Euclidean Distance [u, v]];
cluster = Find Clusters [full_data, 3, Distance Function ® modifieddist, Method ® “Optimize”]
List Plot[cluster, Plot Style ® {Green, Black, Green}]
{Min[First[Transpose[cluster[[2]]]]], Max[First[Transpose[cluster[[2]]]]]}
The following commands were used for data smoothing. The speed of the displacement, “speeds”, was the difference of successive displacement data. “Lowpass Filter” with a filtering frequency of 0.01 defined “filter”, comprised of successive differences of the filtered data. Figure 4 plots “speeds” in green and “filter” in black. In “minutes” the minutes were recorded, when differences of filtered data exceeded the 95% quantile of these differences; t0 and t1 were obtained from the minimum and maximum of minutes.
speeds = Differences[disp_date];
filter = Differences[Lowpass Filter[disp_data, 0.01]];
Show[ListPlot[speeds, PlotStyle ® Green], ListPlot[filter, Plot Style ® Black]]
Minutes =Flatten[Table[If[filter[[n]] > Quantile[filter, 0.95], {n}, {}],
{n, 1, Length[filter]}]]
The following code was used to fit the jump model to the data. It was defined from an interpolation object, that was used like a function: “Interpolation” with the interpolation order 1 defined a piecewise linear function (linear spline) with prescribed values; namely value 0 att = 0 and at t = t0 and value dismax at t = t1 and at t = tmax. “Nonlinear Model Fit” fitted the parameters t0 and t1 to the data using the method of least squares. Thereby, “?NumberQ” was a reminder to the program that these parameters should be used as numbers and not as symbols. Figure 5 plots the original data as green dots and the interpolating object as black curve. Finally, “Best Fit Parameters” retrieved t0, t1, and “AIC” retrieved the Akaike information measure for model selection.
Clear[model];
model[t0_?NumberQ, t1_?NumberQ] = (model[t0, t1] =
Interpolation[{{0, 0}, {t0, 0}, {t1, dismax}, {tmax, dismax}},
InterpolationOrder ® 1]);
splinemod = NonlinearModelFit[full_data, model[t0, t1][t], {t0, t1}, t];
Show[Plot[splinemod[t], {t, 0, tmax}, PlotStyle®Black],
ListPlot[full_data, PlotStyle®Green]]
{splinemod[“BestFitParameters”], splinemod[“AIC”]}
This code was modified as follows for the fit of the linear splines. Here, v0 and v1 were additional parameters that were fit to the data.
model[t0_?NumberQ, t1_?NumberQ, v0_?NumberQ, v1_?NumberQ] =
(model[t0, t1, v0, v1] =
Interpolation[{{0, 0}, {t0, v0}, {t1, v1}, {tmax, dismax}}, InterpolationOrder®1]);
splinemod = NonlinearModelFit[full_data, model[t0, t1, v0, v1][t], {t0, t1, v0, v1}, t];
Appendix III: Data Fitting for the Spline Model in Excel
The raw data have been collected in an Excel file. Its sheet “adobebrick” presents them
Table 1. Excel Sheet for the linear spline approximation.
in the form time vs. displacement. The sheet “pivot” was automatically generated (pivot table in the insert-tab). It computed, for each minute, the average displacements. The model calculations are in the sheet “adobebrick calculations” (see Table 1). The parameters ki and mi of equation (1) were recorded in cells M2:M3 for line d1, in O2:O3 for line d2, and in Q2:Q3 for line d3. From this t0 and t1 were computed in O6:O7 using formula (2). To the right, in column P, time in days was expressed as time in minutes and below, in row 8, the duration of collapse was computed.
For the computation of the linear spline function, the sheet “pivot” was copied into columns A (time in days) and B (average displacement in mm) of the calculation sheet. Column C computes the speed of displacement, the linear functions of formula (1) are computed in columns D to F. From these functions the spline function is pieced together in column G. Column H assesses the fit of this function to the data. Next, in order to apply the method of least squares, in cell I1 the sum of squared residuals is computed as =SUM(H:H). Using the data-tab, the SOLVER add-in is called up and the following optimization model is defined: Minimize cell I1, using as variables cells $M$2; $M$3; $O$2; $O$3; $Q$2; $Q$3, the parameters used in formula (1), and use the nonlinear GRG-solver for this task (EXCEL 2010 and later; in earlier versions just the nonlinear solver). The SOLVER now determines parameters in formula (1) that minimize the sum of squared residuals.
This EXCEL model insofar simplified the linear spline model, as the condition of formula (3) has not been used, because this condition did not have a significant effect on the estimates for t0 and t1. However, the definition of the SOLVER set-up can be easily modified to consider formula (3), too.








