Open Journal of Modelling and Simulation
Vol.04 No.02(2016), Article ID:65553,7 pages
10.4236/ojmsi.2016.42002
AIC-Based Selection of Growth Models: The Case of Piglets from Organic Farming
Katharina Renner-Martin1, Manfred Kühleitner1, Norbert Brunner1, Werner Hagmüller2
1Institute of Mathematics, University of Natural Resources and Life Sciences, Vienna, Austria
2Institute of Organic Farming and Farm Animal Biodiversity, Agricultural Research and Education Centre (AREC), Thalheim/Wels, Austria

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 February 2016; accepted 15 April 2016; published 18 April 2016
ABSTRACT
The selection and comparison of different growth models for describing weight gain of piglets raised in organic farming is investigated by using the Akaike’s Information Criterion (AIC). In total, 49,699 data points of 5188 piglets recorded between 2007 and 2013 were considered. From the day of birth, up to 40 days (i.e. until weaning) the model of von Bertalanffy was favored by the AIC. This model is with 60.32% more likely to truly reflect reality than any other of the analyzed models. Up to 105 days, the two-linear model was favored by the AIC (probability 99.75%). The intersection point of the two-linear model was calculated by 53.8 days, which fitted well to the actual change in the food situations.
Keywords:
AIC, Growth Curve, Growth Model, Weight Gain, Piglet, Organic Farming

1. Introduction
Modeling weight gain or growth of livestock is an important tool for optimizing management decisions and production systems [1] . Amongst considered livestock were cattle [2] - [6] , sheep [7] - [9] , chicken [10] [11] , ducks [12] [13] or turkeys [14] . Several hundred papers deal with growth curves for fisheries.
There exist also studies dealing with the growth patterns of intensive piglet production [15] [16] or a pig breed used as laboratory animal [17] . But organic livestock farming differs from intensive livestock farming in many respects. Animal husbandry, feeding, weaning age and drug administration are the main aspects of that difference. Thus piglets from organic farming are kept under different rearing conditions than piglets in intensive production systems. It is of interest if this difference finds expression in a different growth pattern. Therefore, the aim of this study is the analysis of weight gain of piglets from organic farming.
There are two types of growth models: models with a rather mathematical motivation, such as data fitting (linear or polynomial regression, splines), and models with a biological motivation [18] - [20] . The latter models explain growth e.g. from balancing anabolism and catabolism (von Bertalanffy model). Intermediates between these types are unified approaches, which in essence describe the biologically motivated models by differential equations that generalize the logistic growth model [21] - [23] . As the models differ by the number of parameters, with more parameters enabling a better fit, the model selection is based on the Akaike Information Criterion AIC [24] , which combines the good fit with a penalty for the number of parameters.
Amongst the considered models, only two fitted the piglet data properly: the initial growth phase with only minimal human influence could best be described by the biologically motivated Bertalanffy model, while the long term growth with different phases of human interaction was best described by the two-linear model.
2. Material Studied, Area Descriptions, Methods, Techniques
2.1. Animals and Farm Characteristics
The applied data were recorded in one research center in Upper Austria. In that facility piglets are bred and raised under organic conditions until they reach an age of about 100 days. On that farm there are about 30 breeding sows kept for piglet production. The sows are enabled to litter in farrowing pens. Thus, group suckling is implemented. All piglets were born and raised on that farm.
2.2. Data
A total of 49,699 live weight data were recorded between January 2007 and December 2013 from 5188 piglets aged between 0 and 105 days. The piglets usually were weighed at the day of their birth, at the latest on the first or second days of live, and then once a week. The body weight of each piglet was recorded with a weighing scale with smallest range of 20 g pre-weaning and with an accuracy of 500 g post-weaning and entered in an Excel chart. A macro was programmed to convert the chart in an optimal pattern for editing and analyzing the data.
Some piglets are so-called runts, meaning that they are backward in development and die within the first days or weeks of live. In such a case just a few recordings per piglet exist. Since such animals usually increase less in weight and therefore have a lower body weight than their same-aged conspecifics, a dataset including just the piglets with 6 or more body weight recordings was generated. This dataset contains 48,284 data points of 4393 piglets.
In both datasets, the body weight mean values of each day of live were calculated. The mathematical modeling was performed using these body weight mean values. Data fitting was done in Excel using the Solver add-in and the least squares method.
2.3. Description of the Growth Models
Thirteen growth functions were fitted to the body weight data of the piglets. The equations of the considered growth models are shown in Table 1.
The choice of models was guided by the following aspects: First, in order to avoid numeric integration of differential equations, only models with explicit growth equations were considered. For the same reason, the number of parameters was limited to four. These models include polynomials of degree at most three and splines of two lines (two-linear model), the three biologically motivated models (mentioned in the introduction), and several variants of exponential and logistic growth curves.
2.4. Model Comparison
The models were compared by using Akaike’s Information Criterion (AIC) [24] , which is based on the following benchmark AIC (or more specifically AICL):
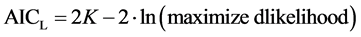 (14)
(14)
where K is the number of parameters in the growth model.
In case of a least squares estimation with normally distributed error term, the following formula can be used to compute the AIC (more precisely: AICS)
Table 1. Functions applied in this study for modeling the growth curve of piglets from organic farming.
y = live weight (kg), t = age (days), a, b, c and d = specific parameters of the growth functions.
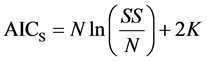 (15)
(15)
where SS is the sum of squares, N is the number of data points and K again is the number of parameters in the model. Due to the fact that both formulas do not show the same result, AIC = AICS in this study.
In general it has to be noted that a conclusion about the quality of the goodness of fit is not possible if the AIC of just one individual model is considered. Only the comparison of several AIC values is convincing. The model with the smallest AIC is said to be the one fitting the data best. The greater the AIC difference the more militates for the model with the smaller AIC value.
The following formula specifies the probability of the right model selection, where D is the difference between two AIC values [25] .
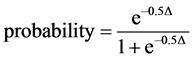 (16)
(16)
The ratio of the relative probabilities of two models can also be calculated directly with
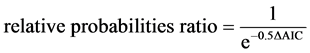 (17)
(17)
3. Results
3.1. Pre-Weaning
Table 2 presents the results up to and including the age of 40 days. The von Bertalanffy model best describes the weight gains of the piglets, followed by the cubic and the quadratic model. The difference of the AIC values between the von Bertalanffy model and the cubic model is 0.837. Therefore the probability of the von Berta-
Table 2. Results pre-weaning.
lanffy model is 60.32%. (This model is with 60.32% more likely than the cubic or any other of the following models.) A graphic representation of the piglets’ body weight mean values of each day of live and the von Bertalanffy model is given in Figure 1.
3.2. From Birth to 105 Days of Age
The results of all piglets from their birth to an age of 105 days are shown in Table 3. The two-linear model has the smallest AIC value and the best fit with a point of intersection at 53.8 days of age. The difference of the AIC values between the two-linear model and the quadratic model is 12.013. Therefore, the probability of the two-linear model is 99.75%. A graphic representation of the piglets’ body weight mean values of each day of live and the two-linear model is given in Figure 2.
4. Discussion
The von Bertalanffy model describes weight gain of piglets in the first weeks of live until weaning best. Considering the whole piglet rearing the most natural nutrition is given during the suckling period. Provided that the piglets remain with the sow the ingested amounts of milk as well as the frequency of suckling are not influenced by the animal owner.
The biologist von Bertalanffy developed his model for all animal species under natural living and nutritional conditions. The model concept is based on physiological processes that are responsible for growth. Growth is defined as a consequence of anabolism and catabolism and will take place as long as building processes outweigh degradation processes. In young animals the primary function of the ingested food is rapid growth, thus it can be seen as a natural limitation of growing capabilities. In this sense the model concept is suited to describe growth development in this early period of live. This model is based on the idea of growth as a biological process until achieving a species-specific weight in adult age. By contrast, during the fattening period the hogs are supplied with much more energy than they would need for natural growth in order to reach as high weight gain as possible in a minimum of time. Thus, the results of the paper confirm that this model appears to be optimal for close to natural conditions.
Among the thirteen growth models the two-linear model describes the weight gain of piglets from organic farming best. This model aims at two different growth periods which actually are caused by the general conditions of the piglets’ rearing. At the age of about 40 days the piglets are weaned. From this moment on the piglets have no longer the opportunity to suckle milk. This implies that solid feed is the only food source and likewise
Figure 1. Body weight mean values of each day of live and the von Bertalanffy model.
Figure 2. Body weight mean values of each day of live and the two-linear model.
Table 3. Results from birth to an age of 105 days.
water is the only source of liquid. Due to the loss of the familiar surroundings the piglets furthermore have to cope with new drinking and feeding troughs, new stable mates, new climate control and also a new germ flora. In addition to the stress attributable to weaning the immune protection of the maternal antibodies that were ingested with the colostrum directly after birth decrease and the piglets’ own immune system is still under development. In this context sometimes antibiotics are administered prophylactically in intensive livestock farming. This is not standard in organic farming with the result that in the first days of post-weaning the weight gain declines or stagnates completely. Not until after coming through that period piglets show an increased weight gain, what corresponds with the point of intersection of the two straight lines of the model at an age of about 50 days. In contrast to De Behr [4] , who described a step-wise linear growth model for Belgian Blue cattle less than 20 month of age, the point of intersection was not fixed in advance, but it was determined from the growth data only through the goodness of fit.
5. Conclusion
Akaike’s Information Criterion points out that not necessarily the model with more parameters (resulting in a better fit) should be recognized as the optimal model, as more parameters may result in an over-fit. Furthermore, AIC allows comparing models that are not nested; also probabilities of models can be calculated. Therefore, Akaike’s Information Criterion provides a comprehensive comparison of all kinds of models. On the basis of this criterion, the initial forty days of growth, where conditions are close to natural ones, can be described by a biologically motivated model. Overall, over 105 days, growth can be described by maximal utilization of food resulting in approximately linear growth, with different slopes depending on the change of the food-situation.
Cite this paper
Katharina Renner-Martin,Manfred Kühleitner,Norbert Brunner,Werner Hagmüller, (2016) AIC-Based Selection of Growth Models: The Case of Piglets from Organic Farming. Open Journal of Modelling and Simulation,04,17-23. doi: 10.4236/ojmsi.2016.42002
References
- 1. Schinckel, A.P. and de Lange, C.F.M. (1996) Characterization of Growth Parameters needed as Inputs for Pig Growth Models. Journal of Animal Science, 74, 2021-2036.
- 2. Brown, J.E., Fitzhugh, H.A. and Cartwright, T.C. (1976) A Comparison of Nonlinear Models for Describing Weight- Age Relationship in Cattle. Journal of Animal Science, 42, 810-818.
- 3. Mara, C.S. and Moura, D.F.A. (1992) Description and comparison of growth parameters in Chianina and Nelore cattle breeds. Genetics and Molecular Biology, 22, 187-196.
- 4. De Behr, V., Hornick, J.L, Cabaraux, J.F., Alvarez, A. and Istasse, L. (2001) Growth patterns of Belgian Blue Replacement Heifers and Growing Males in Commercial Farms. Livestock Production Science, 71, 121-130. http://dx.doi.org/10.1016/S0301-6226(01)00191-9
- 5. Noor, R.R., Saefuddin, A., Talib, C. and Budimulyati, L. (2012) Comparison on Accuracy of Logistic, Gompertz and von Bertalanffy Models in Predicting Growth of New Born Calf Until First Mating of Holstein Friesian Heifers. Journal of the Indonesian Tropical Animal Agriculture, 37, 151-160.
- 6. Vélez, R.V., Noguera, R.R., Posada, S.L., Velásquez, A.H. and Cerón, J.M. (2013) Estimation of Growth in Intact Grazing Holstein Steers. Revista Colombiana de Ciencias Pecuarias, 26, 169-176.
- 7. Widarya, T.R. and Martojo, H.H. (2001) Non-Linear Growth Analysis of Sumatera Thin Tail Sheep and Its Cross Breds. JurnalIlmu Ternakdan Veteriner, 6, 259-264.
- 8. Sarmento, J.L.R., Regazzi, A.J., de Sousa, W.H., de Almeida Torres, R., Breda, F.C. and de Oliveira Menezes, G.R. (2006) Estudo da curva de crescimento de ovinos Santa Inês. Revista Brasileira de Zootecnia, 35, 435-442. http://dx.doi.org/10.1590/S1516-35982006000200014
- 9. Hamouda, M.B. and Atti, N. (2011) Comparison of Growth Curves of Lamb Fat Tail Measurements and Their Relationship with Body Weight in Babarine Sheep. Small Ruminant Research, 95, 120-127. http://dx.doi.org/10.1016/j.smallrumres.2010.10.001
- 10. Aggrey, S.E. (2002) Comparison of Three Nonlinear and Spline Regression Models for Describing Chicken Growth Curves. Poultry Science, 81, 1782-1788. http://dx.doi.org/10.1093/ps/81.12.1782
- 11. Zhao, Z., Li, S., Huang, H., Li, C., Wang, Q. and Xue, L. (2015) Comparative Study on Growth and Developmental Model of Indigenous Chicken Breeds in China. Open Journal of Animal Sciences, 5, 219-223. http://dx.doi.org/10.4236/ojas.2015.52024
- 12. Schinckel, A.P., Adeola, O. and Einstein, M.E. (2005) Evaluation of Alternative Nonlinear Mixed Effects Models of Duck Growth. Poultry Science, 84, 256-264. http://dx.doi.org/10.1093/ps/84.2.256
- 13. Vitezica, Z.G., Marie-Etancelin, C., Bernadet, M.D., Fernandez, X. and Robert-Granie, C. (2010) Comparison of Nonlinear and Spline Regression Models for Describing Mule Duck Growth Curves. Poultry Science, 89, 1778-1784. http://dx.doi.org/10.3382/ps.2009-00581
- 14. Ersoy, I.E., Mendez, M. and Keskin, M. (2007) Estimation of Parameters of Linear and Nonlinear Growth Curve Models at Early Growth Stage in California Turkeys. Archiv für Geflügelkunde, 71, 175-180.
- 15. Schinckel, A.P., Ferrell, J., Einstein, M.E., Pearce, S.A. and Boyd, R.D. (2004) Analysis of Pig Growth from Birth to Sixty Days of Age. The Professional Animal Scientist, 20, 79-86. http://dx.doi.org/10.15232/S1080-7446(15)31276-6
- 16. Wellock, I.J., Emmans, G.C. and Kyriazakis, I. (2004) Describing and Predicting Potential Growth in the Pig. Animal Science, 78, 379-388.
- 17. Köhn, F., Sharifi, A.R. and Simianer, H. (2007) Modeling the Growth of the Goettingen Minipig. Journal of Animal Science, 85, 84-92. http://dx.doi.org/10.2527/jas.2006-271
- 18. Bertalanffy, L. (1957) Quantitative Laws in Metabolism and Growth. The Quarterly Review of Biology, 32, 217-231. http://dx.doi.org/10.1086/401873
- 19. Parks, J.R. (1982) A Theory of Feeding and Growth. Springer, Berlin-Heidelberg-New York.
- 20. Richards, F.J. (1959) A Flexible Growth Function for Empirical Use. Journal of Experimental Botany, 10, 290-300. http://dx.doi.org/10.1093/jxb/10.2.290
- 21. Zeide, B. (1993) Analysis of Growth Equations. Forest Science, 39, 594-616.
- 22. Tsoularis, A. (2001) Analysis of Logistic Growth Models. Research Letters in the Information and Mathematical Sci ences, 2, 23-46.
- 23. Koya, P.R. and Goshu, A.T. (2013) Generalized Mathematical Model for Biological Growths. Open Journal of Modelling and Simulation, 1, 42-53. http://dx.doi.org/10.4236/ojmsi.2013.14008
- 24. Akaike, H. (1974) A New Look at the Statistical Model Identification. IEEE Transactions on Automatic Control, 19, 716-723. http://dx.doi.org/10.1109/TAC.1974.1100705
- 25. Motulsky, H. and Christopoulos, A. (2003) Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. Oxford University Press, Oxford.




