Received 23 April 2015; accepted 1 June 2015; published 5 June 2015

ABSTRACT

Khidr and El-Desouky [1] derived a symmetric sum involving the Stirling numbers of the first kind through the process of counting the number of paths along a rectangular array 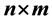denoted by. We investigate the generating function for the general case and hence some special cases as well. The probability function of the number of paths along is obtained. Moreover, the moment generating function of the random variable X and hence the mean and variance are obtained. Finally, some applications are introduced.

Keywords:

Stirling Numbers, Generating Function, Moment Generating Function, Comtet Numbers, Maple Program

1. Introduction

Let 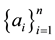be a sequence of natural numbers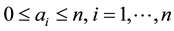, and be an 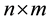array associated with this sequence, whose entries 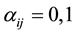such that

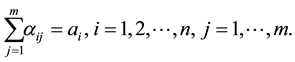
The path of order k along 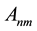is defined to be a sequence of entries 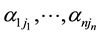as follows

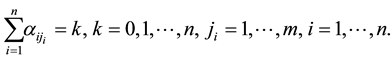
The number of paths of order k will be denoted by

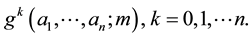
By neglecting the last row in and then reconsidering it, we get the recurrence

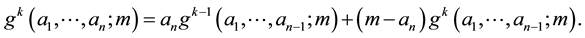(1)

When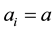, a is a constant, then

(2)

and

Khidr and El-Desouky [1] proved that, when

(3)

where are the generalized Stirling numbers of the first kind associated with the sequence of real numbers, defined by [1] - [6] ,

(4)

These numbers satisfy the recurrence relation

(5)

And

Moreover, they introduced a special case of (3), when, then the number of paths of order k, is denoted by; and proved that

(6)

where are the Stirling numbers of the first kind defined by, see [2] [3]

Also the generating function for is given by

(7)

In this article, in Section 2, we derive a generalization of some results given in [1] , for the number of paths of

order k, , when. The generating function of is given. In Section 3, we find the probability distribution for and study some of their properties. The moment

generating function, skewness and kurtosis for are investigated. Moreover special case and numerical results are given in Section 4.

2. Main Results

Theorem 1. The number of paths of order k is given by

(8)

Proof. Using (5) in (8), we get

This by virtue of (1) completes the proof of (8).

Theorem 2. The generating function of the number of paths of order k is given by

(9)

Proof. Let the generating function of the number of paths of order k be denoted by

(10)

Using (1), we obtain

and hence we get

where. This completes the proof.

From (9), we get

where and hence we have

(11)

where

For the special case, we get

(12)

where

From (6) and (12), we have the identity

(13)

where

3. Some Applications

Let X, be the number of paths along, then by virtue of (8) we have

(14)

On the other hand the moment generating function of the random variable X denoted by, is given by the following theorem.

Theorem 3. The moment generating function of X, is given by

(15)

Proof. We begin by the definition of the moment generating function as follows.

This completes the proof.

Corollary 1. The jth moments of X is

(16)

Proof. The jth moments can be obtained from the moment generating function, where

This completes the proof.

Then from (16), we can calculate the mean and variance for the random variable X as follows.

(17)

(18)

hence the variance is given by

(19)

Corollary 2. The Skewness and kurtosis for the random variable X are given by

(20)

where

Proof. We can find the jth moments about the mean by using

(21)

From (16) and (21), we can find the moments about mean which can be used to calculate the skweness and kurtosis.

Special Case:

If, from (14), we have

and from (16) the jth moments has the form

and the mean is given by

the variance can be obtained as follows.

where we used, see [3] .

4. Numerical Results

Setting. Therefore the numerical values of, are reduced to, see [4] [5] .

From Equation (14), we can find the probability distribution of the number of paths X along as follows

From (16), we can compute the 4th moments as follows.

The 4^th moments about mean can be obtained as

The values of mean and variance can be obtained from (17) and (19) as follows.

The skewness and kurtosis, respectively can be obtained from (20) as follows.

References