Open Journal of Modelling and Simulation
Vol.03 No.01(2015), Article ID:52188,17 pages
10.4236/ojmsi.2015.31001
On the Construction of Analytic-Numerical Approximations for a Class of Coupled Differential Models in Engineering
Emilio Defez1, Vicente Soler2, Roberto Capilla3
1Instituto de Matemática Multidisciplinar, Universitat Politècnica de València, Valencia, Spain
2Departamento de Matemática Aplicada, Universitat Politècnica de València, Valencia, Spain
3Departamento de Ingeniera Electrónica, Universitat Politècnica de València, Valencia, Spain
Email: edefez@imm.upv.es, vsoler@mat.upv.es, rcapilla@eln.upv.es
Academic Editor: Antonio Hervás Jorge, Department of Applied Mathematics, Universidad Politécnica de Valencia, Spain
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 October 2014; revised 1 November 2014; accepted 3 December 2014
ABSTRACT
In this paper, a method to construct an analytic-numerical solution for homogeneous parabolic coupled systems with homogeneous boundary conditions of the type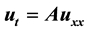 ,
, 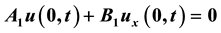 ,
, 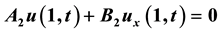 ,
, 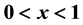 ,
,  ,
, 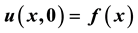 , where
, where 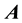 is a positive stable matrix and
is a positive stable matrix and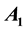 ,
, 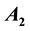 ,
, 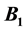 ,
, 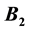 are arbitrary matrices for which the block matrix
are arbitrary matrices for which the block matrix  is non-singular, is proposed.
is non-singular, is proposed.
Keywords:
Coupled Diffusion Problems, Coupled Boundary Conditions, Vector Boundary-Value Differential Systems, Sturm-Liouville Vector Problems, Analytic-Numerical Solution

1. Introduction
Coupled partial differential systems with coupled boundary-value conditions are frequent in different areas of science and technology, as in scattering problems in Quantum Mechanics [1] - [3] , in Chemical Physics [4] - [6] , coupled diffusion problems [7] - [9] , modelling of coupled thermoelastoplastic response of clays subjected to nuclear waste heat [10] , etc. The solution of these problems has motivated the study of vector and matrix Sturm- Liouville problems, see [11] - [14] for example.
Recently [15] [16] , an exact series solution for the homogeneous initial-value problem
 (1)
(1)
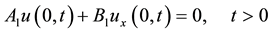 (2)
(2)
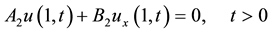 (3)
(3)
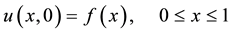 (4)
(4)
where 


tructed under the following hypotheses and notation:
1. The matrix coefficient 

where 





2. Matrices


and also that the matrix pencil

Condition (7) is well known in the literature of singular systems of differential equations, see [17] , and involves the existence of some 




Using condition (7) we can introduce the following matrices 


which satisfy the condition


introduce matrices 


that satisfy the conditions
Under the above assumptions, the homogeneous problem (1)-(4) was solved in [15] [16] in two different cases:
(a) If we consider the following hypotheses:

Then, if the vector valued function 

with the additional condition:

where a subspace 




(b) If we consider the following hypotheses:

Then, if the vector valued function 

under the additional condition:

then we can construct an exact series solution 
Observe that under the different hypotheses (a) and (b), the exact solution of problem (1)-(1) is given by the series

where, under hypothesis (a), the value of 

and 



with an additional solution 

and under hypothesis (b), the value of 

and 



with an additional solution 

Under both hypotheses (a) and (b), the value of




and

taking 

The series solution of problem (1)-(4) given in (16) presents some computational difficulties:
(a) The infiniteness of the series.
(b) Eigenvalues 

(c) Other problem is the calculation of the matrix exponential, which may present difficulties, see [21] [22] for example.
For this reason we propose in this paper to solve the following problem:
Given an admissible error 




This paper deals with the construction of analytic-numerical solutions of problem (1)-(4) in a subdomain


construct the approximate solution. In Section 3 we will introduce an algorithm and give an illustrative example.
Throughout this paper we will assume the results and nomenclature given in [15] [16] . If 


where for a vector 



Let us introduce the notation

and by ( [23] , p. 556) it follows that

2. The Proposed Approximation
Let


Thus, we can take a positive constant

satisfying

Moreover, by (23), we have
If we define 

we have that

On the other hand, we know from (27) that
where, as



where

Observe that for a fixed 



then

Taking into account that 



and by (34) there is a positive integer 

Using (29), (31), (32) and (36), if
As eigenvalues


Taking into account that


We take the first positive integer 

We define the vector valued function 

Using (38) one gets that
thus

Remark 1. Note that to determine the positive integer 
knowledge the exact eigenvalues

and by (35), we can replace condition (36) by take the first positive integer 

Approximation 





where


with 

It is easy to see that


and

Replacing in (47) and taking norms, one gets

We define 


by applying the Cauchy-Schwarz inequality for integrals and (28), one gets:
We have
Taking 

it follows that

Moreover, working component by component:


Applying the Cauchy-Schwarz inequality for integrals again:

and


By (55) and taking into account (57) and (58):

Note that from the definition of

then, replacing in (60) one gets

We take

then, if we define

from (54) we have that

and from (62) and (53):

Using the 2-norm properties, from (66) we have

By other hand, we can write
where taking norm, applying (32) and (33) together the mean value theorem, under the hypothesis
where

Replacing in (51) we obtain

where

Given 





then
and therefore

Remark 2. From (61), and taking into account the definition of 

so that, if 


Similarly, can be taken in practice

instead of the definition (63).
Approximation 





We define the approximation 

and from (65), (64) and (45) one gets that
We take

and suppose we make the approximation accurate enough satisfying condition

Thus, if 

and from (42), (72) and (78):
Summarizing, the following results has been established:
Theorem 1. We consider problem (1)-(4) satisfying hypotheses (5), (6) and (7). Let















Let 






Suppose that the approximations 











Theorem 2. We consider problem (1)-(4) satisfying hypotheses (5), (6) and (7). Let






defined by (20), (26), (28) and (68) respectively. Let 





the interval






















3. Algorithm 1, Algorithm 2 and Example
We can give the following algorithms, according to the hypothesis (a) or (b) is satisfied, to construct the approximation
Algorithm 1. Construction of the analytic-numerical solution of problem (1)-(4) under hypotheses (a) in the subdomain 


Algorithm 2. Construction of the analytic-numerical solution of problem (1)-(4) under hypotheses (b) in the subdomain 


Example 1. We will construct an approximate solution in the subdomain



and the 


Also, the vectorial valued function 

This is precisely the example 1 of Ref. [15] whose exact solution is given by:

We will follow algorithm 1 step by step:
1. Hypothesis (a) holds with



is regular. Therefore, we take
2. Performing calculations similar to those made in Ref. [15] , one gets that


3. It is easy to calculate





4. Note that
Then, by (43):
then we take
5. We have
then we can take
6. We need to determinate the 
We can solve exactly this equation, 


and then
In summary, 





7. We calculate 

the smallest of them is


8. We have that



9. We have that
10. To be applicable the algorithm 1, the approximations 
As the roots were calculated with 50 decimal accurate, we accept these approximations of the roots.
11. We have to take 
12. We have to compute approximations 





then, we can obtain 

13. Functions

14. Vectors

We don’t compute 

15. Compute 
where
and our approximation satisfies
As an example, consider the point
It is easy to check that, from (82), one gets
4. Conclusion
In this paper, a method to construct an analytic-numerical solution for homogeneous parabolic coupled systems with homogeneous boundary conditions of the type (1)-(4) has been presented. An algorithm with an illustrative example is given.
References
- Alexander, M.H. and Manolopoulos, D.E. (1987) A Stable Linear Reference Potencial Algorithm for Solution of the Quantum Close-Coupled Equations in Molecular Scattering Theory. The Journal of Chemical Physics, 86, 2044-2050. http://dx.doi.org/10.1063/1.452154
- Melezhik, V.S., Puzynin, I.V., Puzynina, T.P. and Somov, L.N. (1984) Numerical Solution of a System of Integro-Differential Equations Arising from the Quantum-Mechanical Three-Body Problem with Coulomb Interaction. Journal of Computational Physics, 54, 221-236. http://dx.doi.org/10.1016/0021-9991(84)90115-3
- Reid, W.T. (1971) Ordinary Differential Equations. Wiley, New York.
- Levine, R.D., Shapiro, M. and Johnson, B. (1970) Transition Probabilities in Molecular Collisions: Computational Studies of Rotational Excitation. The Journal of Chemical Physics, 53, 1755-1766. http://dx.doi.org/10.1063/1.1673214
- Schmalz, T.G., Lill, J.V. and Light, J.C. (1983) Imbedded Matrix Green's Functions in Atomic and Molecular Scattering theory. The Journal of Chemical Physics, 78, 4456-4463. http://dx.doi.org/10.1063/1.445338
- Mrugala, F. and Secrest, D. (1983) The Generalized Log-Derivate Method for Inelastic and Reactive Collisions. The Journal of Chemical Physics, 78, 5954-5961. http://dx.doi.org/10.1063/1.444610
- Crank, J. (1995) The Mathematics of Diffusion. 2nd Edition, Oxford University Press, Oxford.
- Mikhailov, M.D. and Osizik, M.N. (1984) Unifield Analysis and Solutions of Heat and Mass Diffusion. Wiley, New York.
- Stakgold, I. (1979) Green’s Functions and Boundary Value Problems. Wiley, New York.
- Hueckel, T., Borsetto, M. and Peano, A. (1987) Modelling of Coupled Thermo-Elastoplastic Hydraulic Response of clays Subjected to Nuclear Waste Heat. Wiley, New York.
- Atkinson, F.V. (1964) Discrete and Continuous Boundary Value Problems. Academic Press, New York.
- Atkinson, F.V., Krall, A.M., Leaf, G.K. and Zettel, A. (1987) On the Numerical Computation of Eigenvalues of Sturm? Liouville Problems with Matrix Coefficients. Technical Report, Argonne National Laboratory.
- Marletta, M. (1991) Theory and Implementation of Algorithms for Sturm-Liouville Systems. Ph.D. Thesis, Royal Military College of Science, Cranfield.
- Greenberg, L. (1991) A Prüfer Method for Calculating Eigenvalues of Self-Adjoint Systems of Ordinary Differential Equations, Parts 1 and 2. Technical Report TR91-24, University of Maryland.
- Soler, V., Defez, E., Ferrer, M.V. and Camacho, J. (2013) On Exact Series Solution of Strongly Coupled Mixed Parabolic Problems. Abstract and Applied Analysis, 2013, Article ID: 524514.
- Soler, V., Defez, E. and Verdoy, J.A. (2014) On Exact Series Solution for Strongly Coupled Mixed Parabolic Boundary Value Problems. Abstract and Applied Analysis, 2014, Article ID: 759427.
- Campbell, S.L. and Meyer Jr., C.D. (1979) Generalized Inverses of Linear Transformations. Pitman, London.
- Navarro, E., Jódar, L. and Ferrer, M.V. (2002) Constructing Eigenfunctions of Strongly Coupled Parabolic Boundary Value Systems. Applied Mathematical Letters, 15, 429-434. http://dx.doi.org/10.1016/S0893-9659(01)00154-9
- Pryce, J.D. (1993) Numerical Solution of Sturm-Liouville Problems. Clarendon, Oxford.
- Pryce, J.D. and Marletta, M. (1992) Automatic Solution of Sturm-Liouville Problems Using Pruess Method. Journal of Computational and Applied Mathematics, 39, 57-78. http://dx.doi.org/10.1016/0377-0427(92)90222-J
- Moler, C.B. and Van Loan, C.F. (1978) Nineteen Dubious Ways to Compute the Exponential of a Matrix. SIAM Review, 20, 801-836. http://dx.doi.org/10.1137/1020098
- Moler, C.B. and Van Loan, C.F. (2003) Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later. SIAM Review, 45, 3-49.
- Golub, G.H. and Van Loan, C.F. (1989) Matrix Computation. The Johns Hopkins University Press, Baltimore.
- Coddington, E.A. and Levinson, N. (1967) Theory of Ordinary Differential Equations. McGraw-Hill, New York.
- Sastre, J., Ibáñez, J., Ruiz, P. and Defez, E. (2014) Accurate and Efficient Matrix Exponential Computation. International Journal of Computer Mathematics, 91, 97-112. http://dx.doi.org/10.1080/00207160.2013.791392
- Sastre, J., Ibáñez, J., Defez, E. and Ruiz, P. (2011) Accurate Matrix Exponential Computation to Solve Coupled Differential Models in Engineering. Mathematical and Computer Modelling, 54, 1835-1840. http://dx.doi.org/10.1016/j.mcm.2010.12.049
- Sastre, J., Ibáñez, J., Defez, E. and Ruiz, P. (2011) Efficient Orthogonal Matrix Polynomial Based Method for Computing Matrix Exponential. Applied Mathematics and Computation, 217, 6451-6463.
- Dunford, N. and Schwartz, J. (1977) Linear Operators, Part I. Interscience, New York.










































