Open Journal of Modelling and Simulation
Vol.2 No.2(2014), Article ID:44344,11 pages DOI:10.4236/ojmsi.2014.22005
Effects of Hall Current on Flow of Unsteady MHD Axisymmetric Second-Grade Fluid with Suction and Blowing over an Exponentially Stretching Sheet
Haider Zaman1, Arif Sohail1, Azhar Ali2, Tarique Abbas2
1Faculty of Numerical Sciences, Islamia College University, Peshawar, Pakistan
2Sarhad University of Science and Information Technology, Peshawar, Pakistan
Email: haiderzaman67@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 10 January 2014; revised 15 February 2014; accepted 25 February 2014
ABSTRACT
This paper investigates effects of Hall current on flow of unsteady magnetohydrodynamic (MHD) axisymmetric second-grade fluid with suction and blowing over a sheet stretching exponentially with radius. The governing non-linear partial differential equations describing the problem are converted to a system of non-linear ordinary differential equations by using the similarity transformations. The complex analytical solution is found by using the homotopy analysis method (HAM). The existing literature on the topic shows that it is the first study regarding the effects of Hall current on flow over an exponentially stretching sheet in cylindrical coordinates. The convergence of the obtained complex series solutions is carefully analyzed. The effects of dimensionless parameters on the radial and axial components of the velocity are illustrated through plots. Also the effects of the pertinent parameters on the shear stress at the wall are presented numerically in tabular form.
Keywords:Hall Currents; Unsteady; Axisymmetric; Suction/Blowing; Exponential Stretching

1. Introduction
The theoretical study of boundary layer flows induced by a stretching sheet [1] is of considerable interest because their applications in fibers spinning, manufacturing of plastic and rubber sheets, the aerodynamic extrusion of plastic sheets, hot rolling and cooling of an infinite metallic plate in a cooling bath. Partha et al. [2] studied the effect of viscous dissipation on the mixed convection heat transfer from an exponentially stretching surface. Sajid and Hayat [3] extended this problem by investigating the radiation effects on the flow over an exponentially stretching sheet, and solved the problem analytically using the homotopy analysis method. The numerical solution for the same problem was then given by Bidin and Nazar [4] . Recently Ishak [5] investigated the thermal radiation effects on hydro-magnetic flow due to an exponentially stretching sheet. Magyari and Keller [6] investigated the steady boundary layers on an exponentially stretching continuous surface with an exponential temperature distribution. In recent years the theoretical study of Effects of Hall current on MHD flows has been a subject of great interest due to its widely spread applications in power generators and pumps, Hall accelerators, refrigeration coils, electric transformers, in flight MHD, solar physics involved in the sunspot development, the solar cycle, the structure of magnetic stars, electronic system cooling, cool combustors, fiber and granular insulation, oil extraction, thermal energy storage and flow through filtering devices and porous material regenerative heat exchangers. Usually Hall term representing the Hall current was ignored in applying Ohm’s law, because it has no remarkable effect for small and moderate values of the magnetic field. The effects of Hall current are very important if the strong magnetic field is applied [7] , because for strong magnetic field electromagnetic force is noticeable. The recent investigation for the applications of MHD is towards a strong magnetic field, due to which study of Hall current is important. In presence of a strong magnetic field in an ionized gas of low density, the conductivity normal to the magnetic field is decreased by free spiraling of electrons and ions about the magnetic lines of force before suffering collisions. A current induced in a direction normal to the electric and magnetic fields is called Hall current [8] . Some interesting old and new studies regarding the effects of Hall current on MHD flow are done by [9] -[17] .
The present investigation is to analyze the effects of Hall current on flow induced by an exponentially stretching sheet of unsteady MHD axisymmetric second-grade fluid with suction and blowing. Here, we assume that sheet is stretching exponentially with the radius. The existing literature on the topic shows that effects of Hall current on an axisymmetric flow over an exponentially stretching sheet in cylindrical coordinates have not been investigated so far. The arising non-linear problem is solved by the homotopy analysis method (HAM), which is a novel technique and has been used by many researchers [18] -[26] .
2. Mathematical Formulation of the Problem and Analytic Solution
We consider the unsteady flow of an electrically conducting incompressible second-grade fluid over a porous exponentially stretching sheet placed in the plane 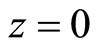 in the presence of transverse magnetic field. The cylindrical coordinates
in the presence of transverse magnetic field. The cylindrical coordinates 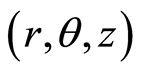 are used and it is assumed that the flow takes place in the upper half plane
are used and it is assumed that the flow takes place in the upper half plane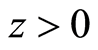 . We assume rotational symmetry of the flow so all physical quantities are independent of θ i.e.
. We assume rotational symmetry of the flow so all physical quantities are independent of θ i.e. , the azimuthal component of velocity
, the azimuthal component of velocity  vanishes identically. It is assumed that the sheet is being stretched with an exponential velocity
vanishes identically. It is assumed that the sheet is being stretched with an exponential velocity , where
, where 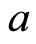 is the reference velocity and
is the reference velocity and 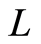 is the reference radius. The Cauchy stress tensor
is the reference radius. The Cauchy stress tensor 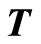 for a second-grade fluid is given as [27]
for a second-grade fluid is given as [27]
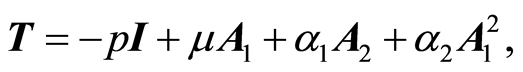 (1)
(1)
where 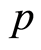 is the scalar pressure,
is the scalar pressure, 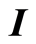 is the identity tensor,
is the identity tensor,  is the coefficient of viscosity,
is the coefficient of viscosity, 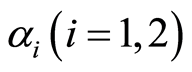 are the material parameters of second-grade fluid, and
are the material parameters of second-grade fluid, and  are the first two Rivlin-Ericksen tensors defined by [28]
are the first two Rivlin-Ericksen tensors defined by [28]
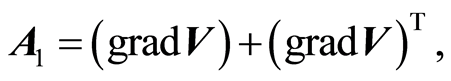 (2)
(2)
 (3)
(3)
It is assumed that the flow meets the Clausius-Duhem inequality and that the specific Helmholtz free energy of the fluid is minimum at equilibrium [29] when
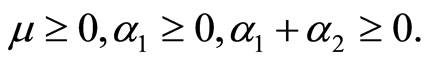 (4)
(4)
For detailed analysis about the signs of these normal stress moduli one may see [30] . The equations governing the magnetohydrodynamic flow with Hall effects are:
Velocity field:
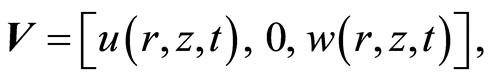 (5)
(5)
Continuity equation:
 (6)
(6)
Equation of motion:
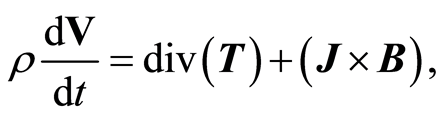 (7)
(7)
Equations for the stream function:
 (8)
(8)
Maxwell equations:
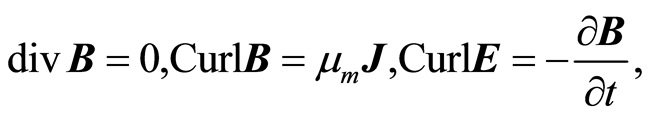 (9)
(9)
Generalized Ohm’s law:
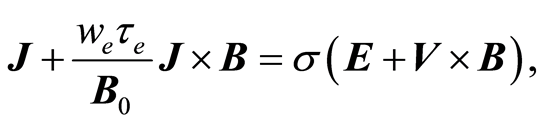 (10)
(10)
where 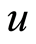 is the radial velocity and
is the radial velocity and 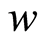 is the axial velocity,
is the axial velocity, 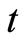 is time,
is time,  is the total magnetic field,
is the total magnetic field,  is the applied magnetic field,
is the applied magnetic field, 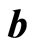 is the induced magnetic field,
is the induced magnetic field, 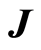 is the current density,
is the current density,  is the electrical conductivity of the fluid,
is the electrical conductivity of the fluid, 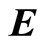 is the electric field,
is the electric field, 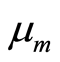 is the magnetic permeability,
is the magnetic permeability, 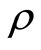 is the fluid density,
is the fluid density, 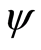 is the stream function,
is the stream function,  and
and 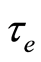 are the cyclotron frequency and collision time of the electrons respectively. We assume that, the quantities
are the cyclotron frequency and collision time of the electrons respectively. We assume that, the quantities 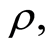
 and
and 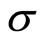 are constants throughout the flow field, the magnetic field
are constants throughout the flow field, the magnetic field  is normal to the velocity vector
is normal to the velocity vector 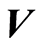 and the induced magnetic field is neglected compared with the imposed magnetic field, so that the magnetic Reynolds number is small [31] . We also suppose that
and the induced magnetic field is neglected compared with the imposed magnetic field, so that the magnetic Reynolds number is small [31] . We also suppose that  and
and 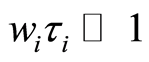 (where
(where 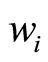 and
and 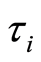 are the cyclotron frequency and collision time for ions respectively). The radial velocity is zero far from the sheet and the pressure is uniform, so we neglect the pressure gradient term [32] . Under aforementioned assumptions and using the boundary layer approximations [33] , the unsteady problem with Hall currents become
are the cyclotron frequency and collision time for ions respectively). The radial velocity is zero far from the sheet and the pressure is uniform, so we neglect the pressure gradient term [32] . Under aforementioned assumptions and using the boundary layer approximations [33] , the unsteady problem with Hall currents become
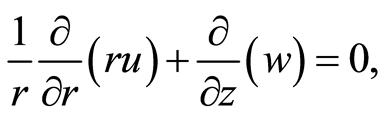 (11)
(11)
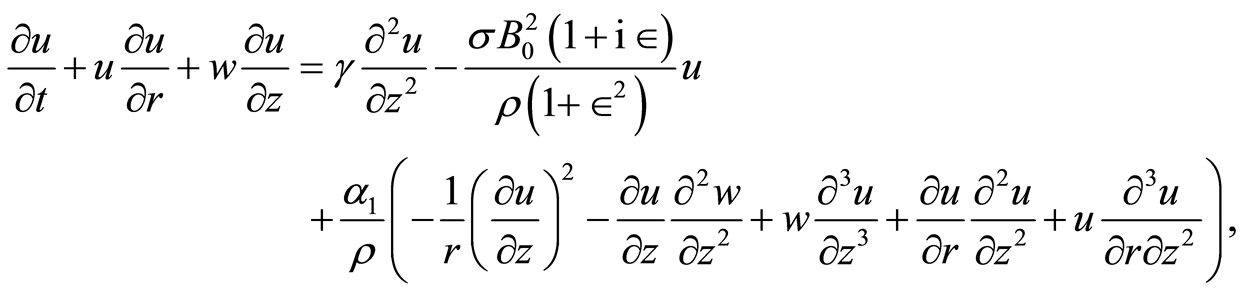 (12)
(12)
The boundary conditions applicable to the flow are
 (13)
(13)
where  is the kinematic viscosity,
is the kinematic viscosity, 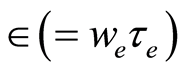 is the Hall parameter and
is the Hall parameter and  is the suction or blowing velocity in the
is the suction or blowing velocity in the , the positive sign denotes suction while negative sign denotes blowing. In order to nondimensionalize the problem let us introduce the similarity transformations
, the positive sign denotes suction while negative sign denotes blowing. In order to nondimensionalize the problem let us introduce the similarity transformations
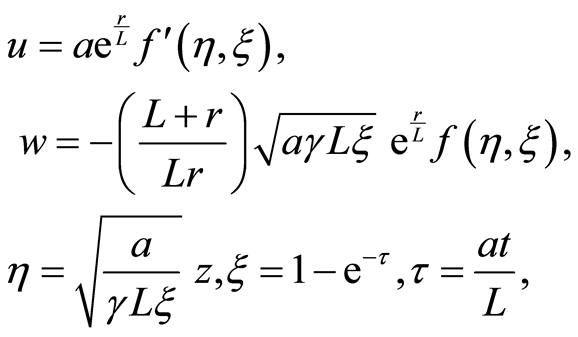 (14)
(14)
where 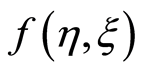 is the dimensionless stream function. Equation (11) is identically satisfied and Equations (12) and (13) become [16]
is the dimensionless stream function. Equation (11) is identically satisfied and Equations (12) and (13) become [16]
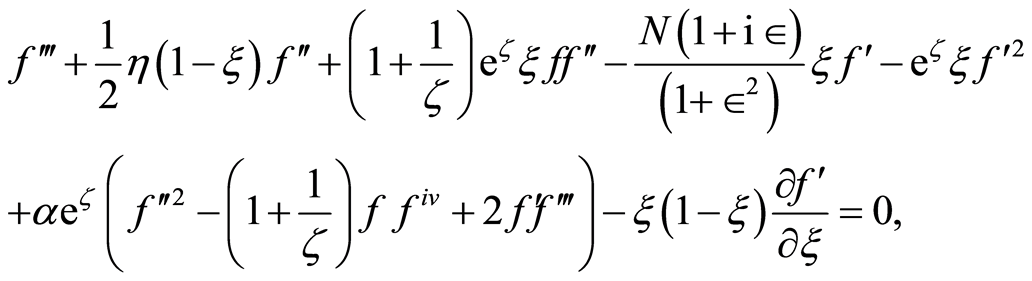 (15)
(15)
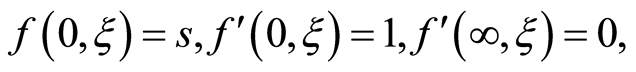 (16)
(16)
where prime denotes differentiation with respect to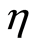 ,
,  is the dimensionless modified Hartmann number [31] ,
is the dimensionless modified Hartmann number [31] ,  is a dimensionless coordinate,
is a dimensionless coordinate,  is the dimensionless second grade fluid parameter and
is the dimensionless second grade fluid parameter and  is the dimensionless suction or blowing parameter,
is the dimensionless suction or blowing parameter,
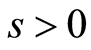 corresponds to suction and
corresponds to suction and 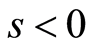 corresponds to blowing. The local skin friction coefficient or fractional drag coefficient on the surface of the exponentially stretching sheet is
corresponds to blowing. The local skin friction coefficient or fractional drag coefficient on the surface of the exponentially stretching sheet is
 (17)
(17)
Now using Equations (1), (2), (3) and (14), Equation (17) can be written in dimensionless variables as
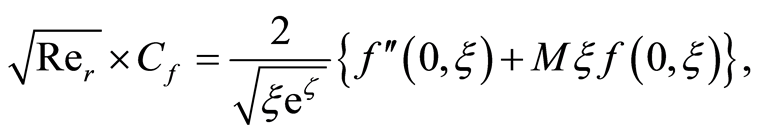 (18)
(18)
where 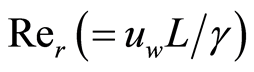 is the local Reynolds number and
is the local Reynolds number and 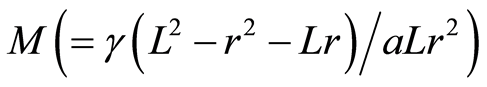 is a dimensionless constant. Note that Equation (18) is obtained by taking
is a dimensionless constant. Note that Equation (18) is obtained by taking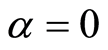 , for
, for  it is too difficult to find it.
it is too difficult to find it.
To start with the homotopy analysis method, due to the boundary conditions (16) it is reasonable to choose the initial guess approximation and the auxiliary linear operator
 (19)
(19)
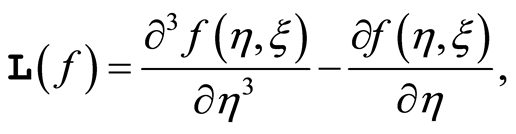 (20)
(20)
where  satisfy
satisfy
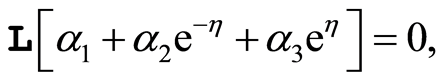 (21)
(21)
where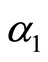 ,
, 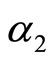 and
and 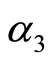 are arbitrary constants. Following the HAM and trying higher iterations with the unique and proper assignment of the results converge to the exact solution:
are arbitrary constants. Following the HAM and trying higher iterations with the unique and proper assignment of the results converge to the exact solution:
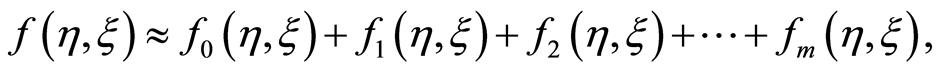 (22)
(22)
Using the symbolic computation software such as MATLAB, MAPLE, MATHEMATICA to successively obtain
 (23)
(23)
similarly ,
, 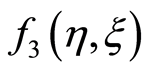 ,
, 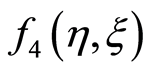 and so on are calculated. The obtained values of
and so on are calculated. The obtained values of ,
, 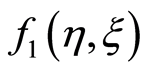 ,
, 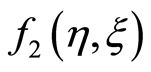 , - - - -leads us to take
, - - - -leads us to take
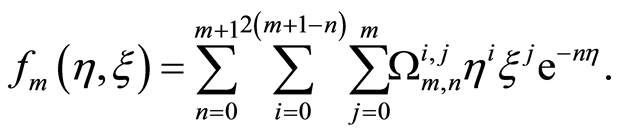 (24)
(24)
After very lengthy calculations we arrive at the total complex analytic solution in compact form as
 (25)
(25)
where from initial guess in Equation (19) we obtain
 (26)
(26)
all other unknown constants can be determined by utilizing first four given in Equation (26) by using the recurrence relations, which we calculated but it is not possible to write here due to their length.
3. Graphs, Tables and Discussion
Here we discuss the convergence of the analytic solution and effect of emerging parameters on the radial and axial velocities of the fluid. The auxiliary parameter , gives the convergence region and rate of approximation for the homotopy analysis method. The
, gives the convergence region and rate of approximation for the homotopy analysis method. The 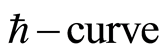 is plotted for real part of axial velocity
is plotted for real part of axial velocity 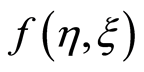 and from Figure 1 we observe that
and from Figure 1 we observe that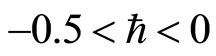 . Our calculations depict that the series of the dimensionless stream function in Equation (26) converges in the whole region of
. Our calculations depict that the series of the dimensionless stream function in Equation (26) converges in the whole region of  and
and 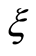 for
for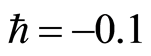 . Figure 2 indicates the variation of the real part of the axial velocity
. Figure 2 indicates the variation of the real part of the axial velocity 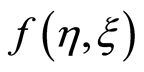 with η for suction. This figure shows that in case of suction for fixed values of
with η for suction. This figure shows that in case of suction for fixed values of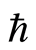 , N,
, N, 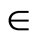 ,
,  ,
,  and s with increase in dimensionless time ξ real part of the axial velocity decreases. In Figure 2 boundary layer structure is observed and the boundary layer thickness increases with increasing time
and s with increase in dimensionless time ξ real part of the axial velocity decreases. In Figure 2 boundary layer structure is observed and the boundary layer thickness increases with increasing time , which results in thickening of the boundary layer, which is used in recognition of the
, which results in thickening of the boundary layer, which is used in recognition of the

Figure 1.  for
for .
.
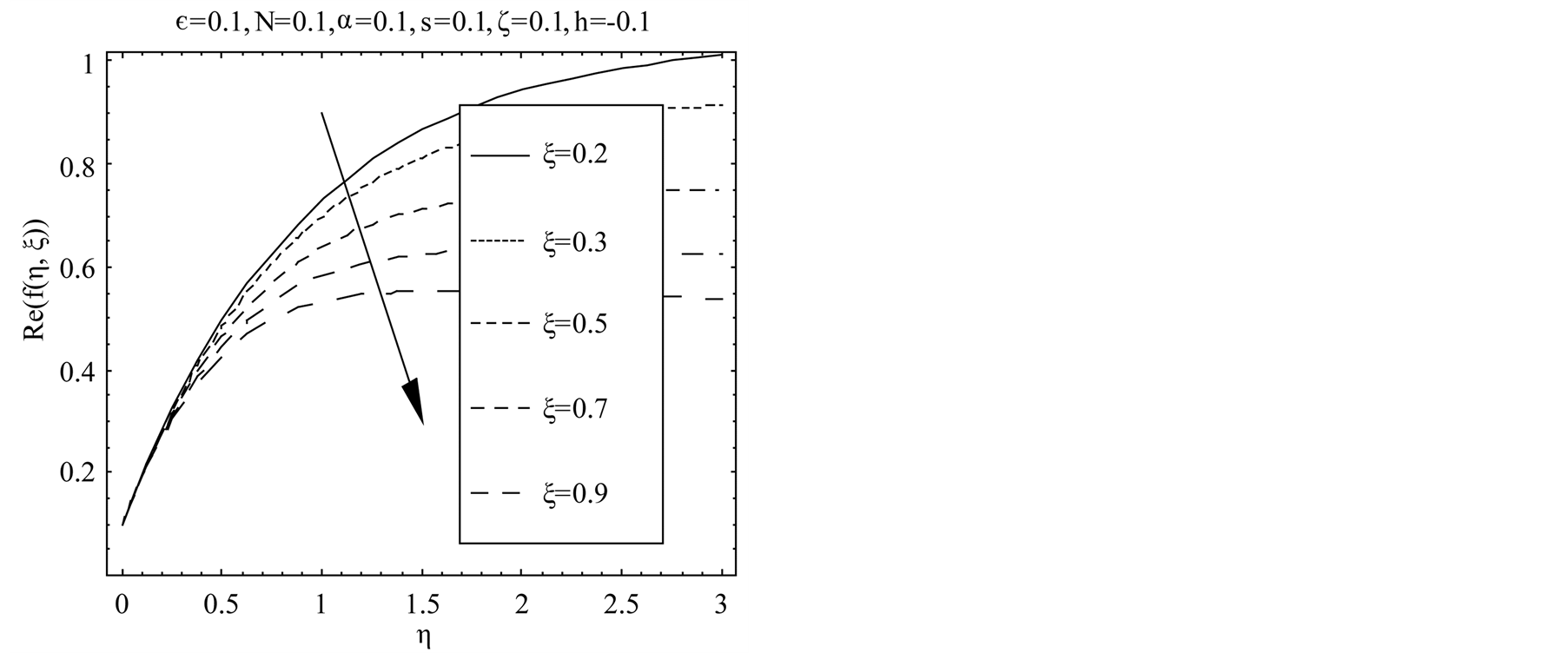
Figure 2. Influence of  on
on .
.
fluid. Figure 3 elucidates that in case of blowing with the increase in Hall current  imaginary part of the axial velocity
imaginary part of the axial velocity  decreases in magnitude and boundary layer thickness increases with increasing Hall current
decreases in magnitude and boundary layer thickness increases with increasing Hall current . Figure 4 illustrates that with the increase in second-grade parameter
. Figure 4 illustrates that with the increase in second-grade parameter 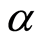 real part of the axial velocity
real part of the axial velocity  increases for blowing. Figure 5 describes that for suction with the increase in exponential stretching parameter
increases for blowing. Figure 5 describes that for suction with the increase in exponential stretching parameter 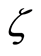 imaginary part of the axial velocity
imaginary part of the axial velocity  decreases in magnitude and boundary layer thickness increases with increasing
decreases in magnitude and boundary layer thickness increases with increasing  and shear thickening effects are seen. Figure 6 represents that in case of suction with increase in dimensionless time
and shear thickening effects are seen. Figure 6 represents that in case of suction with increase in dimensionless time 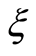 real part of the radial velocity
real part of the radial velocity  decreases. Clearly the viscosity induces in the fluid with the passage of time and after some time the steady state is achieved which proves the uniform validity of the solution for all time in the whole spatial region
decreases. Clearly the viscosity induces in the fluid with the passage of time and after some time the steady state is achieved which proves the uniform validity of the solution for all time in the whole spatial region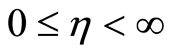 . Figure 7 shows that with the increase in second-grade parameter
. Figure 7 shows that with the increase in second-grade parameter 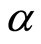 real part of the radial velocity
real part of the radial velocity  increases for blowing. Figure 8 describes that for blowing with the increase in exponential stretching parameter
increases for blowing. Figure 8 describes that for blowing with the increase in exponential stretching parameter  real part of the radial velocity
real part of the radial velocity 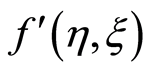 increases.
increases.
Tables 1 and 2 are prepared for the variation of the absolute values of the shear stress at the wall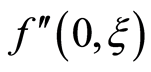 . It is observed from Table 1 that for suction and blowing for fixed values of N,
. It is observed from Table 1 that for suction and blowing for fixed values of N,  ,
,  ,
, 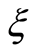 and
and  with increase in second-grade fluid parameter
with increase in second-grade fluid parameter 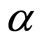 absolute values of the shear stress at the wall
absolute values of the shear stress at the wall  decreases. It is also observed from Table 1 that with increase in Hall current
decreases. It is also observed from Table 1 that with increase in Hall current 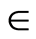 absolute values of the
absolute values of the 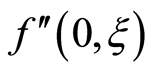 decreases for suction and blowing. When magnetic field is applied normal to the fluid velocity then it gives rise to a drag-like or resistive force which slow down or suppress the motion of the fluid on the stretching surface. This leads to a re-
decreases for suction and blowing. When magnetic field is applied normal to the fluid velocity then it gives rise to a drag-like or resistive force which slow down or suppress the motion of the fluid on the stretching surface. This leads to a re-

Figure 3. Influence of  on
on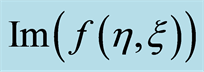 .
.

Figure 4. Influence of  on
on .
.

Figure 5. Influence of  on
on .
.

Figure 6. Influence of  on
on .
.

Figure 7. Influence of 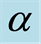 on
on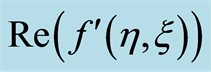 .
.
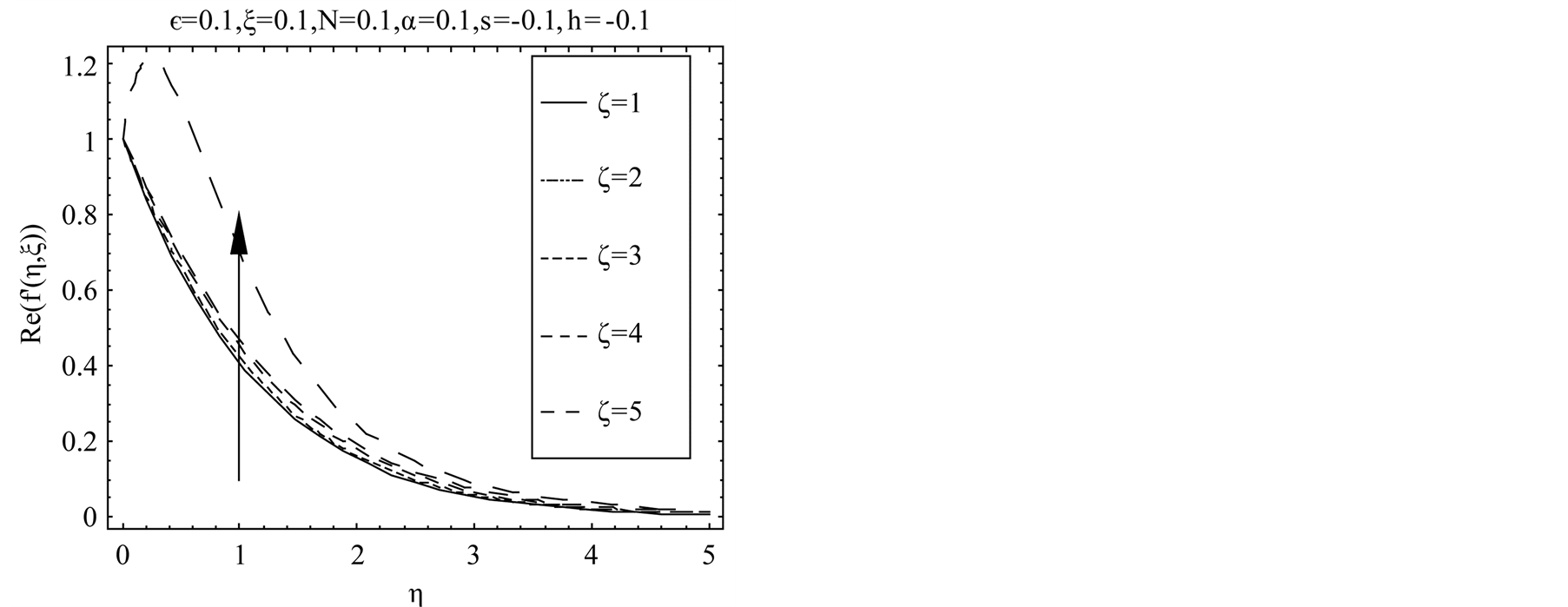
Figure 8. Influence of  on
on .
.
duction in the velocity of the fluid and flow rates. With the increase in the strength of the magnetic field the motion of the particulate suspension on the surface reduces due to which shear stress at the wall reduces with increase in 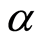 and
and , as observed in Table 1. From Table 1 we note that with increase in dimensionless time
, as observed in Table 1. From Table 1 we note that with increase in dimensionless time 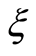 the absolute values of the
the absolute values of the  increases.
increases.
Table 1. Absolute values of the shear stress at the wall  with
with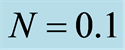 ,
,  ,
, .
.
Table 2. Absolute values of the shear stress at the wall 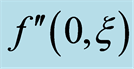 with
with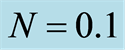 ,
,  ,
, .
.
Table 2 shows that for fixed values of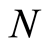 ,
,  ,
, 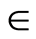 ,
, 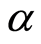 and
and  with increase in exponential stretching
with increase in exponential stretching 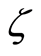 absolute value of the
absolute value of the 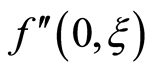 decreases for suction and blowing. Also with increase in Hall parameter
decreases for suction and blowing. Also with increase in Hall parameter 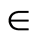 the absolute values of the
the absolute values of the  decreases for suction and blowing.
decreases for suction and blowing.
4. Conclusion
Effects of Hall current on flow of unsteady MHD axisymmetric second-grade fluid with suction and blowing over an exponentially stretching sheet are seen first time. The present complex explicit analytic solution is uniformly valid for all dimensionless time in the entire flow regime. Convergence of the solution is appropriately discussed. Graphical and tabular results for Hall parameter , second-grade parameter
, second-grade parameter , exponentially stretching parameter
, exponentially stretching parameter 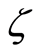 and dimensionless time
and dimensionless time 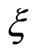 reveal that Hall parameter, second-grade parameter, exponential stretching and dimensionless time have a significant influence on the radial and axial components of velocity.
reveal that Hall parameter, second-grade parameter, exponential stretching and dimensionless time have a significant influence on the radial and axial components of velocity.
References
- Zaman, H. (2009) Flows Induced by a Stretching Surface. Ph.D. Thesis, Quaid-i-Azam University Islamabad, Islamabad.
- Partha, M.K., Murthy, P.V.S.N. and Rajasekhar, G.P. (2005) Effect of Viscous Dissipation on the Mixed Convection Heat Transfer from an Exponentially Stretching Surface. Heat Mass Transfer, 41, 360-366. http://dx.doi.org/10.1007/s00231-004-0552-2
- Sajid, M. and Hayat, T. (2008) Influence of Thermal Radiation on the Boundary Layer Flow Due to an Exponentially Stretching Sheet. International Communications in Heat and Mass Transfer, 35, 347-356. http://dx.doi.org/10.1016/j.icheatmasstransfer.2007.08.006
- Bidin, B. and Nazar, R. (2009) Numerical Solution of the Boundary Layer Flow over an Exponentially Stretching Sheet with Thermal Radiation. European Journal of Scientific Research, 33, 710-717.
- Ishak, A. (2011) MHD Boundary Layer Flow Due to an Exponentially Stretching Sheet with Radiation Effect. Sains Malaysiana, 40, 391-395.
- Magyari, E. and Keller, B. (1999) Heat and Mass Transfer in the Boundary Layers on an Exponentially Stretching Continuous Surface. Journal of Physics D: Applied Physics, 32, 577-585. http://dx.doi.org/10.1088/0022-3727/32/5/012
- Cramer, K. and Pai, S. (1973) Magnetofluid Dynamics for Engineers and Applied Physicists. McGraw-Hill, New York.
- Sato, H. (1961) The Hall Effects in the Viscous Flow of Ionized Gas between Parallel Plates under Transverse Magnetic Field. Journal of the Physical Society of Japan, 16, 1427-1433. http://dx.doi.org/10.1143/JPSJ.16.1427
- Katagiri, M. (1969) The Effect of Hall Currents on the Magnetohydrodynamic Boundary Layer Flow past a Semi-Infinite Flate Plate. Journal of the Physical Society of Japan, 27, 1051-1059. http://dx.doi.org/10.1143/JPSJ.27.1051
- Pop, I. and Soundalgekar, V.M. (1974) Effects of Hall Current on Hydromagnetic Flow near a Porous Plate. Acta Mechanica, 20, 315-318. http://dx.doi.org/10.1007/BF01175933
- Gupta, A.S. (1975) Hydromagnetic Flow past a Porous Flate Plate with Hall Effects. Acta Mechanica, 22, 281-287. http://dx.doi.org/10.1007/BF01170681
- Debnath, L., Ray, S.C. and Chatterjee, A.K. (1979) Effects of Hall Current on Unsteady Hydromagnetic Flow past a Porous Plate in a Rotating Fluid System. Z. Angew. Mathematical Mechanism, 59, 469-471. http://dx.doi.org/10.1002/zamm.19790590910
- Khan, M., Asghar, S. and Hayat, T. (2009) Hall Effect on the Pipe Flow of a Burgers’ Fluid: An Exact Solution. Nonlinear Analysis: Real World Applications, 10, 974-979. http://dx.doi.org/10.1016/j.nonrwa.2007.11.016
- Hayat, T., Zaman, H. and Ayub, M. (2010) Analytic Solution of Hydromagnetic Flow with Hall Effect over a Surface Stretching with a Power Law Velocity. Numerical Methods for Partial Differential Equations, 27, 937-959. http://dx.doi.org/10.1002/num.20562
- Ahmad, M., Zaman, H. and Rehman, N. (2010) Effects of Hall Current on Unsteady MHD Flows of a Second Grade Fluid. Central European Journal of Physics, 8, 422-431. http://dx.doi.org/10.2478/s11534-009-0083-z
- Ayub, M., Zaman, H. and Ahmad, M. (2010) Series Solution of Hydromagnetic Flow and Heat Transfer with Hall Effect in a Second Grade Fluid over a Stretching Sheet. Central European Journal of Physics, 8, 135-149. http://dx.doi.org/10.2478/s11534-009-0110-0
- Zaman, H. (2013) Hall Effects on the Unsteady Incompressible MHD Fluid Flow with Slip Conditions and Porous Walls. Applied Mathematics and Physics, 1, 31-38.
- Liao, S.J. (2003) Beyond Perturbation: Introduction to Homotopy Analysis Method. Chapman and Hall, CRC Press. http://dx.doi.org/10.1201/9780203491164
- Liao, S.J. (1992) The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problem. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai.
- Liao, S.J. (2012) Homotopy Analysis Method in Nonlinear Differential Equations. Higher Education Press, Beijing, Springer-Verlag, Berlin, Heidelberg. http://dx.doi.org/10.1007/978-3-642-25132-0
- Liao, S.J. (2013) Advances in the Homotopy Analysis Method. World Scientific Publishing Company, Singapore.
- Liao, S.J. (2009) Notes on the Homotopy Analysis Method: Some Definitions and Theorems. Communications in Nonlinear Science and Numerical Simulation, 14, 983-997.
- Liao, S.J. (2006) An Analytic Solution of Unsteady Boundary-Layer Flows Caused by an Impulsively Stretching Plate. Communications in Nonlinear Science and Numerical Simulation, 11, 326-339.
- Ayub, M., Zaman, H., Sajid, M. and Hayat, T. (2008) Analytical Solution of Stagnation-Point Flow of a Viscoelastic Fluid towards a Stretching Surface. Communications in Nonlinear Science and Numerical Simulation, 13, 1822-1835. http://dx.doi.org/10.1016/j.cnsns.2007.04.021
- Zaman, H. and Ayub, M. (2010) Series Solution of Unsteady Free Convection Flow with Mass Transfer along an Accelerated Vertical Porous Plate with Suction. Central European Journal of Physics, 8, 931-939. http://dx.doi.org/10.2478/s11534-010-0007-y
- Zaman, H., Hayat, T., Ayub, M. and Gorla, R.S.R. (2011) Series Solution for Heat Transfer from a Continuous Surface in a Parallel Free Stream of Viscoelastic Fluid. Numerical Methods for Partial Differential Equations, 27, 1511-1524. http://dx.doi.org/10.1002/num.20593
- Rivlin, R.S. and Ericksen, J.L. (1955) Stress Deformation Relations for Isotropic Materials. Journal of Rational Mechanics and Analysis, 4, 323-425.
- Bandelli, R. and Rajagopal, K.R. (1995) Start-Up Flows of Second Grade Fluids in Domains with one Finite Dimension. International Journal of Non-Linear Mechanics, 30, 817-839. http://dx.doi.org/10.1016/0020-7462(95)00035-6
- Dunn, J.E. and Fosdick, R.L. (1974) Thermodynamics, Stability and Boundedness of Fluids of Complexity 2 and Fluids of Second Grade. Archive for Rational Mechanics and Analysis, 56, 191-252. http://dx.doi.org/10.1007/BF00280970
- Dunn, J.E. and Rajagopal, K.R. (1995) Fluids of Differential Type: Critical Review and Thermodynamic Analysis. International Journal of Engineering Science, 33, 689-729. http://dx.doi.org/10.1016/0020-7225(94)00078-X
- Sutton, G.W. and Sherman, A. (1965) Engineering Magnetohydrodynamics. McGraw-Hill, New York.
- Prasad, K.V., Datti, P.S. and Raju, B.T. (2013) Momentum and Heat Transfer of a Non-Newtonian Eyring-Powell Fluid over a Non-Isothermal Stretching Sheet. International Journal of Mathematical Archive, 4, 230-241.
- White, F.M. (1991) Viscous Fluid Flow. McGraw-Hill, New York.


