Advances in Historical Studies
Vol.05 No.05(2016), Article ID:73175,16 pages
10.4236/ahs.2016.55017
Charles-Augustin Coulomb―The Founder of Physiology and Ergonomics
Agamenon R. E. Oliveira
Polytechnic School of Rio de Janeiro, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 3, 2015; Accepted: December 27, 2016; Published: December 30, 2016
ABSTRACT
The memoir Sur la force des Hommes was published by Coulomb in 1778. It is an attempt to understand human work mechanically and is the first publication on physiology and ergonomics. The question introduced by Coulomb appears from a pragmatic point of view. He proposed to measure the quantity of action (mechanical work) that a man can expend in a day of work by different ways of applying force. To do this, Coulomb studied the old problem of human mechanical capacity, also studied by Theophilus Desagulliers (1683-1744) and Daniel Bernoulli (1700-1782). In this paper we examine and discuss Coulomb’s above-mentioned publication showing his pioneering approach ( Coulomb, 2002 ).
Keywords:
History of Sciences, History of Biomechanics, History of the Work Concept, History of Mechanics

1. Introduction
The science of biomechanics is the study of the structure and function of biological systems such as the human body, animals, plants, organs and cells, using the methods of mechanics. This discipline is closely related to engineering and notwithstanding some old studies; we consider that it only appeared after the establishment of Newtonian mechanics. Common applications are Newtonian mechanics and materials sciences to find the correct approach to obtain the necessary approximations to represent many biological systems ( Oomens & Brekelmans, 2009 ). Auxiliary disciplines include: continuum mechanics, mechanisms analysis, structural analysis, kinematics and dynamics. Numerical methods are normally used and applied in almost biomechanical studies where the steps of modelling, computer simulations, and experimental measurements are present, similar to other branches of mechanics. The most important fields of biomechanics are: continuum biomechanics, biofluid mechanics, biotribology, comparative biomechanics, plant biomechanics, computational biomechanics and others.
In recent decades with the development of new technologies, mainly nanotechnologies ( Lourtioz & Lahmani, 2013 ), the field of biomechanics has expanded considerably, giving rise to the new discipline of nanomechanics, also called nanoscale biomechanics. This field belongs to a biomedical technology that involves the measurement of the mechanical characteristics of individual cells. This is done using instruments that can produce, detect, and measure forces of the order of a few piconewtons. Nanobiomechanics is therefore part of the larger field of nanoscale biomedical research ( Douglas, 2016 ).
Coulomb is recognized as one of the founders of electricity and magnetism theories. His name designates the unit of electrical charge. However, it is not well known that a great part of his work is dedicated to mechanical problems. The theory of friction was developed by him, for which he was awarded the Grand Prix by the French Academy of Sciences in 1781 ( Oliveira, 2013 ).
His memoir Sur la force des Hommes, occupies a particular place in his scientific work. Coulomb left the School of Mézière in 1761, going to Martinique, where he spent eight years as military engineer. There he was appointed to build the Bourbon Fort, following a tradition that came from Vauban (1633-1707). This was the motivation to study the productive capacity of men, fundamental knowledge for organizing and programming large military works. His memoir was therefore a consequence of this experience.
2. Fundamental Steps in the Development of Biomechanics
・ The first study in biomechanics is attributed to Aristotle (384-322 BC). He wrote a book called De Motu Animalium, in which he looked at animal bodies as mechanical systems.
・ With the decline of Greece and the rise of the Roman Empire, Galen (129-200/216 AD), physician of the Roman emperor Marcus Aurelius (121-180 AD), made his name. His book On the Function of the Parts, meaning the parts of the human body, became the standard medical text for the next 1400 years.
・ In the Renaissance, in the middle of the second millennium, Leonardo da Vinci (1452-1519), became famous as an artist, but also as an engineer. He had a good qualitative understanding of the components of vector forces, friction coefficients and the accelerating falling of bodies. His studies of anatomy, in the context of mechanics and the analyses of muscle forces acting inside human body, were of great importance to biomechanics.
・ Galen was finally overtaken when in 1543 the Flemish physician Andreas Vesalius (1514-1564) published the illustrated book On the Structure of the Human Body. Some of Galen’s errors were corrected by Vesalius.
・ Galileo (1564-1642) also made important contributions to biomechanics. He made the following remarks in his Discorsi (1638):
a) Animal mass does not increase proportionally to size, thus their bone resistance must also not increase proportionally.
b) The bending stresses of a tubular structure such as a bone increases relative to its weight resulting it in being hollow and increasing its diameter.
c) At sea animals can be larger and heavier than terrestrial animals, because of the water’s buoyancy.
・ Giovanni Afonso Borelli (1608-1679), is often described as the father of biomechanics, because his work De Motu Animalium (1680) applied the analytical methods developed by Galileo. He calculated the forces required for the equilibrium of human body. Hence, Borelli understood perfectly the role of the lever principle to magnify motion. Because of his importance to biomechanics, the American Society of Biomechanics grants the Giovanni Borelli Award.
・ Julien Offray de la Mettrie (1709-1751) was a French physician and philosopher, one of the first French materialists of the Enlightenment. He is known for his L’homme machine (1680). He believed that man worked like a machine and that the organization of matter at a high and complex level produces human thought.
・ Jacques de Vaucanson (1709-1782) was a French inventor and artist responsible for the creation of automata and machines like the completely automated loom. His Digesting Duck (1739) had the ability to eat kernels of grain and to metabolize and defecate them.
3. Coulomb: A Biographical Note
Charles Augustin Coulomb (Figure 1(a)) was born in Angoulême, France on June 14, 1736. His father was Henry Coulomb and his mother was Cathérine Bajet. Both his parents came from families which were well known and important in their regions. After being brought up in Angoulême, the capital of Angoumois in southwestern France, Coulomb’s family moved to Paris. In Paris he entered Collège Mazarin, where he received a good classical education in language, literature and philosophy. He received the best available education in mathematics, astronomy, chemistry and botany.
After a period in Montpellier, Coulomb went to Paris in October 1758 to receive the tutoring necessary to take the entrance examinations for École du Génie in Mézières. He studied Camus’ famous book, Cours de Mathematique for several months. In the same year, Coulomb took the examinations set by Camus himself. He passed and he entered the École du Génie in February 1760, the same school from which Lazare Carnot would graduate in 1773.
Coulomb graduated in November 1761, now a trained engineer with the rank of lieutenant in the Corps du Génie. Over the next twenty years he lived and worked in several places where he was involved in engineering, structural design, fortifications, soil mechanics and many other areas. After his first posting in Brest in 1764 he was sent to Martinique in the West Indies. However, Martinique was attacked by a number of foreign fleets over the following years and finally captured by England in 1762.
On his return to France, Coulomb was sent to Bouchain. He now began to write important works on applied mechanics and in 1773 he presented his first work to the Académie des Sciences in Paris. This was entitled: “Sur une Application des règles, de maximis et minimis à quelque problème de statique, relatifs à l’architecture.” The most significant aspect of this work is Coulomb’s use of the calculus of variation to solve the problem under consideration.
In 1779 Coulomb was sent to Rochefort. During his time there he began his investigations into mechanics, using the local shipyards as laboratories for his experiments. His studies of friction forces led him to write the major work: Théorie des Machines Simples (Figure 1(b)).
This 1781 memoir changed completely Coulomb’s life. He was elected to the mechanics section of the Académie des Sciences, and moved to Paris where he now held a permanent post ( Rashed, 1998 ). He devoted the following years mainly to physical problems rather than engineering. He wrote treatises on electricity and magnetism, also submitted to the Académie des Sciences between 1785 and 1791.
Between 1781 and 1806 he presented twenty-five memoires to the Académie des Sciences. He also carried out several investigations during this period with Bossut (1730-1814), Borda (1733-1799), de Prony (1755-1839) and Laplace (1749-1827), as well as participating in the work of 310 Academy committees. Besides these engineering projects, he also carried out services for the French government in several fields from education to hospital reform. His educational activities were largely carried out between 1802 and 1806, when he was inspector general of public instruction He was also mainly responsible for setting up the Lycées across France. Coulomb died in Paris on August 23, 1806.

Figure 1.(a) Charles-Augustin Coulomb (1736-1806); (b) Théorie des Machines Simples.
4. Coulomb’s sur la Force des Hommes
This publication is written in a simple almost colloquial style similar to a monograph or an end-of-course work. It has 42 pages and is divided as follows:
・ Introduction.
・ The quantity of actions that men can perform, during a day’s work, going up a ramp or stairs, both carrying and not carrying a load.
・ Comparison between the quantity of actions that men can perform while on a horizontal path, both carrying and not carrying a load.
・ The quantity of actions that men can perform during a day’s work transporting loads in a wheelbarrow.
・ The quantity of actions that men can perform in a motion, lifting a load and dropping in piles.
・ Men cranking handles.
・ The quantity of action that men can perform in a day’s work while digging with an excavator.
・ Conclusion.
Some remarks should be made here. Quantity of action ( Carnot, 1803 ) in fact means work in the modern physical meaning, in general as a product of forces multiplied by the displacement of their points of application. The term work was coined by Coriolis in 1829 in his Du Calcul des Effets des Machines. The main concern expressed by Coulomb refers to the calculation of the quantity of actions that a man can provide in a day’s work incorporating the internal expense of energy associated with human fatigue. This component of human work and how it is estimated is different from measuring its external mechanical process. It is not a question of applying forces to a weight and calculating the work transmitted to it but estimating its effect on the human body ( Vatin, 1993 ).
4.1. Introduction
Coulomb begins the introduction of his text writing: The human body is composed of different flexible parts, animated by an intelligent principle linked to several forms and positions which from this point of view is almost every time a machine is suitable to develop composite motions with continuum variations and many possibilities in relation to pressure, velocity and direction. He continues: Two things can distinguish the work of men and animals when we apply force to a given machine, the effect produced and the fatigue resulting from this process. In order to obtain the maximum possible result, it is necessary to increase the effect without increasing the fatigue, and by supposing that we have a formula to represent the effect and other to represent the fatigue. It is also necessary to represent the effect divided by the fatigue and that this ratio becomes a maximum.
Some important things are clearly expressed here. The idealization of human or animal bodies by machine representation. The idea of modelling mathematically the ratio between effect and fatigue and an indication of how to find the best solution using a method of optimization. A kind of system efficiency is suggested and will be discussed later.
Coulomb uses the very popular eighteenth century approach to calculating the effect or the work done by a machine as the product of a weight by the height achieved. In relation to fatigue it is necessary to identify it by means of an action. This action can be measured by the pressure that a man can exert multiplied by the velocity and the elapsed time of the action. Another way to estimate fatigue is by using the analogy of a machine and calculating the weight and the height that a man can lift during a single day.
Daniel Bernoulli is referred to by Coulomb because the former stated that fatigue is always proportional to the quantity of action (work); consequently, to measure fatigue we have to make variations of the velocity, pressure, and time parameters. Taking into account that the product of these three quantities is constant, for a given man his degree of fatigue is the same. Bernoulli estimated that in a single day of any kind of work is equivalent to lifting 1,728,000 pounds one foot, or 274,701 kilograms one meter.
Desaguilliers is also referred to by Coulomb, who recognizes that the majority of authors who studied this problem performed experiments and obtained approximately the same results. It is important to emphasize that these experiments were very limited in time and care must be taken to use these values for one day’s work.
Coulomb finishes this item highlighting the difference in his method which does not consider the proportionality between the quantity of action (work) and fatigue as postulated by Daniel Bernoulli. Rather he uses a function of the following parameters: actual pressure, velocity of the pressure point, and the elapsed time of work.
4.2. The Quantity of Action That Men Can Perform, during a Day’s Work, Going up a Ramp or Stairs, Both Carrying and Not Carrying a Load
In this item, Coulomb’s objective is to build a mathematical model representing the work that a man can perform during a single working day, with the characteristic of incorporating the fatigue effect. His initial steps are aimed at numerically estimating the parameters appearing in the model whose values can be accepted as adequate for this phenomenon. Hence, he discusses the simple problem of going up a ramp (Figure 2) with a height of between 20 and 50 meters, estimating that this can be done at a velocity of 14 m/min. The quantity of action achieved in this kind of work in a minute must be multiplied by the man’s weight and the height to be reached. Considering an average weight for the worker of 70 kg, the work performed per minute will be 70 kg multiplied by 14 or, 980 kg raised to one meter. Assuming that the man can perform this work for four hours per day, the daily quantity of action will be equal to 235,200 kg raised to a height of a meter.
Considering another type of work, let us suppose that a man is walking up a hill for one day. He can perform a quantity of action obtained by the multiplication of his weight 70 kg by 2923 meters which is also supposed what can be achieved in one day. This is equivalent to 204,610 kg raised to one meter, which is approximately the same as the previous one.
Figure 2. Work done moving a load up a ramp.
To build a mathematical model representing a man going up a ramp, we can suppose as a first approximation that the lost quantity of action is proportional to the load. Then, as an example, if we call P the load to be lifted, the quantity of action that this load can lose is equal to 96/68 P = 1.41 P, estimated by the ratio between the load of 68 kg when he goes up the ramp with a load of 96 kg for one kilometer.
Thus, we can write: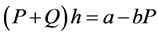 , where
, where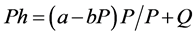 , which is the net effect.
, which is the net effect.
Differentiating the net effect function with respect to P we obtain (1):
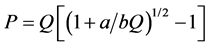 (1)
(1)
Substituting the numerical values of a, b and Q, one obtains: P = 53 kg.
Substituting this value of P in the net effect function, one obtains Ph = 56 kg raised to one meter.
Coulomb remarks that with this type of work in which men carry loads, go back down, and again carry a new load, they can only perform a net work of 56 kg raised to one kilometer. Considering men going upwards without a load, they can achieve 205 kg raised to one kilometer.
Coulomb not only established a useful approach for obtaining numerical values for the model’s parameters in the model, but also made some checks to test the model itself. He takes the formula (205 − 1.41P) and equates it to zero, obtaining P = 145 kg. This is the maximum weight that a man with a medium force can raise over a very short distance. He concludes that the model gives two limits at the same time. The maximum value for the total action of a man going up freely without a load and the minimum of action with the man going up carrying a very large weight that he cannot move far from an intermediate value of 68 kg given by experience.
The mathematical model proposed by Coulomb in fact incorporated some economic concerns in the study ( Vatin, 1998 ). It is worth remembering his main motivation was the production and the construction of engineering fortifications. His modelling uses the idea of work, called at this time quantity of action, something very common in the eighteenth century. The mechanical capacity that a machine can give is calculated by the weight that it can lift multiplied by the height achieved by this weight. It is interesting remarking that Coulomb considers the human body to be a machine. This analogy is essential for building the model. The attempt made by Coulomb to incorporate fatigue as a fundamental component of his model is simple and involves considering a linear polynomial formula and the numerical values for the parameters are obtained by engineering experience.
4.3. Comparison between the Quantity of Action That Men Can Perform While on Horizontal Path, Both Carrying and Not Carrying a Load
To estimate the numerical values for the parameters in this second type of motion, the quantity of action performed on a horizontal path (Figure 3), Coulomb supposes that a man can displace in a single day, around 50 km. If his weight is 70 kg, as assumed previously, one multiplies 70 kg by 50 km, such that one obtains 3500 kg displaced one kilometer. The objective of this exercise is to compare the quantity of action that a man can perform in one day’s work both without a load and displacing a load. It is, thus, supposed that a man can transport furniture from one place to another with a distance of 2 km carrying a load of 58 kg, doing this 6 times per day. Remembering that the man has a weight of 70 kg with a load of 58 kg, displaced 2 km, in each trip 128 kg will be carried. Multiplying 6 trips by 128 kg by 12 km, we obtain 1536 kg displaced one kilometer.
The inclusion of fatigue after 12 km is made by assuming that the man can walk 50 km and that in doing this he uses approximately one quarter of his daily work. As a result, the 1536 kg displaced one kilometer represents three quarters of his daily work. As result, the quantity of action that men can achieve in a day with a load of 58 kg can be estimated as equivalent to 2048 kg displaced one kilometer. After some interviews with workers that did this type of work, Coulomb concluded that is acceptable to consider for day’s work that a quantity of action equivalent to displacing 2000 kg one kilometer can be performed. Thus, the daily quantity of action which is lost in a load of 58 kg is equivalent to 1500 kg displaced one kilometer. If we suppose that losses measured in terms of quantity of action are proportional to load and x is the quantity of action that this load loses, we have (2):
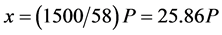 (2)
(2)
Figure 3. Work done moving a load along a horizontal plane.
Then, daily quantity of action which can be supplied by a man carrying the load P is equal to the lost quantity of action in function of the load P, whose daily quantity of action is:
3500 − 25.86 P, where 3500 represents 3500 multiplied by 1 km and the number 25.86 represents kilometers.
If we look at this formula we can find the largest weight that a man can displace, or the weight which ceases the motion. Equating (3500 − 25.86 P) = 0, where P = 135.4 kg, which means the force that a man of medium capacity can displace in a very short time. This equation establishes the limit to human capacity for this type of work, also assuming that the quantity of action is proportional to load.
Similarly to the previous section, we are concerned with the load that a man can displace for the maximum net effect. We suppose that a man carrying the load P, in his daily work, displaces the load along the space l, whose daily quantity of action is obtained, adopting Q = 70 kg, which is the weight of his body. Then, 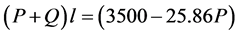 , represents the quantity of action when the man carries the weight P; thus, we have (3):
, represents the quantity of action when the man carries the weight P; thus, we have (3):
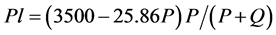 (3)
(3)
where the quantity Pl represents the load multiplied by the space that is displaced, giving the net effect of the work. This quantity must be maximized. To do this we adopt P as the independent variable and the differentiation of the function must be equated to 0, to obtain the maximum effect. If we call 3500 = a and 25.86 = b, differentiating and equating to 0, one obtains (4):
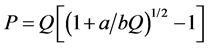 (4)
(4)
Substituting numerical values, P = 0.72, Q = 50.4 kg.
As adopted before, l = 50 km, the length that a man can displace in one day, without a load, assuming that Q = 70 kg, the weight of his body, Ql will be the quantity of action that he can perform during the day’s work without a load; if he displaces without a load the space x less than l, Qx will be part of his daily work. Dividing Qx/Ql or x/l will be part of his daily work without a load. The unity will be the totality, because x becomes l, x/l will be equal to 1.
Because a man can displace along the same path x whether carrying a load or not, since the load is P, we can find the action that he can perform in a day’s work is equal to 3500 − 25.86 P; then, part of the action under the load P is represented by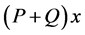 , a relation that represents part of the quantity of daily action which he achieved with a load. Therefore, for this fraction of work
, a relation that represents part of the quantity of daily action which he achieved with a load. Therefore, for this fraction of work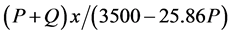 ; taking into account that the addition of both works, with a load and walking freely is equal to the day’s work, we have (5):
; taking into account that the addition of both works, with a load and walking freely is equal to the day’s work, we have (5):
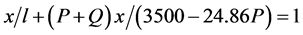 (5)
(5)
If we consider Ql = 3500, which is the quantity obtained by the multiplication of the weight of the man by the path which he can follow in one day’s work without a load, we can consider h = 25.86 km; then, the previous equation becomes (6):
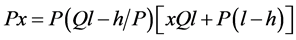 (6)
(6)
where Px expresses part of the net effect that a man can achieve in one day. This is the quantity that we must maximize, differentiating this function with P as the independent variable and equating to 0. We have for P, after substituting numerical values, the following: P = 61.25 km and Px = 692.4 kg displaced one kilometer. This value for P implies the best net effect for the quantity of action. Coulomb makes small variations of P around 4 and 5 kg and concludes that the model used also present small variations for the net effect. This analysis is a kind of study of parameter sensitivity.
The mathematical model used in this second item is similar to what is used in the previous item. However, Coulomb compares physically these two types of work, lifting a load vertically and displacing a load horizontally, and the fatigue implications associated with both.
4.4. The Quantity of Action That Men Can Achieve in a Day’s Work Moving Loads by Wheelbarrow
Initially, Coulomb remarks that the type of work analyzed in this item is the type most employed in civil and military engineering involving the movement of earth. He also quotes the famous engineer Vauban, emphasizing that the latter left the results of his experiences in instructions published in Bélidor’s Science of Engineers. Vauban wrote:
A man in his daily work can move by wheelbarrow 14.79 m3 of earth a distance of 29,226 m; this total quantity is made 500 times: thus, he displaces the load 14,613 km, including the unloaded wheelbarrow.
Coulomb also discusses Vauban’s citation. He wrote that after the load is placed in the wheelbarrow (Figure 4) the man lifts the wheelbarrow’s arms to approximately 15 dm, carrying part of load and part of wheelbarrow’s weight. The remainder of the weight is supported by the ground in the contact with the wheelbarrow’s wheel. In another comment, Coulomb states that to transport the wheelbarrow’s load, men hold around 18 to 20 kg, while with the empty wheelbarrow they hold only 5 to 6 kg. In addition, the force to push the wheelbarrow is about 3 kg, also depending on irregularities along the trajectory.
Figure 4. Work done conveying weight with wheelbarrows.
After these initial considerations about this type of work, Coulomb tries to study the net quantity of action in a day’s work. He considers the medium load carried by wheelbarrows as around 70 kg; while the weight of unloaded wheelbarrows is approximately 30 kg. Taking into account that the net effect is measured by the multiplication of the quantity of earth carried times the path’s length, the loaded wheelbarrow with 14.61 km of distance, the net daily effect will be the product: 70 × 14.6 = 1022.7 kg displaced one kilometer.
Considering the maximum net effect that a man can provide carrying a load on his shoulders is 692.4 kg displaced one kilometer, the maximum net effect for the same man displacing a load by wheelbarrow will be in the following proportion: 1022.7:692.4:148:100 on dry horizontal terrain, 100 men with wheelbarrows perform approximately the same quantity of action as 150 men.
4.5. The Quantity of Action That Men Can Provide in a Motion Lifting One Weight and Dropping It Fall in Piles
In the action of men lifting weights and dropping them in piles (Figure 5), the net effect achieved is calculated by the weight lifted, the height achieved by the weights, and the number of movements that occurred in a day’s work. Normally the weights are around 350 to 450 kg. The system is such that a wire passed through a pulley with the weight at one extremity and the lifting mechanism at the other. In this type of motion 20 swinging moves per minute are assumed, with 60 to 80 successive moves, followed by intervals of rest. It was observed that men lift around 11 dm to trigger the system.
According to Coulomb, for this type of work, men can rarely do more than three hours of actual work in a day; the complimentary time is used for different types of rest, while they lift around 19 kg of weight.
The quantity of daily action for this type of work is calculated by the product of three numbers: 11 dm, 19 kg and the number of swinging moves in three hours of actual work with 20 swings per minute; this gives an equivalent quantity of action of 75 kg raised to one kilometer.
If we compare this work with the quantity of action for a man going up a ramp which was calculated previously as 205 kg elevated to one kilometer, it is easy to see that it represents one third of the action produced by the second case.
Figure 5. Work done dropping weights on piles.
4.6. Men Cranking a Handle
Coulomb remarks that for this type of work many observations with machines were made. However, the resistance that men can offer is difficult to estimate.
From these observations, in the majority of mechanical works the pressure that a man can exert by hand cranking a handle (Figure 6) is around 12 to 13 kg. However, in continuous work this pressure normally is around 7 kg. This hand motion frequently follows a circle of 23 dm of circumference performing 30 turns per minute. If the number of observations is increased, maintaining the pressure of 7 kg, they can only turn the handle 22 times per second.
Figure 6. Work done by turning a crank.
The time of a day’s work is 10 hours. In long periods of works we can consider only 8 hours of actual work or 6 hours of timed work with 20 turns per minute. To calculate the quantity of action after these observations, we have to multiply the numbers 7 kg, 35 dm, 20 and 360; this gives the daily quantity of action of 116 kg elevated to one kilometer.
Looking at these results, if we compare different quantities of action provided by men going up stairs freely with men cranking handles, we can find for the same man the numbers 205 and 116 or the numbers 8.5 which gave a good approximation for all practical points of view.
4.7. The Quantity of Action That Men Use in a Day’s Work Digging with an Excavator
In relation to this type of work, there is a great variety of results, depending on the nature of terrain, the seasons of the year, and even the weather in which the work is carried out, and how the area and its surface was left by workers.
Coulomb refers to previous experience using 8000 m2 and a vigorous intelligent worker with familiarity with excavators (Figure 7). The worker was paid per square meter and in one day’s work he can earn 2 francs and 50 centimes. An excavator of 25 cm was used and in each swing of the excavator he lifted 6 kg more or less. Furthermore, he moved his center of gravity center to a variable height of around 4 dm. This motion has a frequency of 20 swings per minute. The first one penetrates the soil some centimeters with an opposition force of about 12 kg.
Figure 7. Work done by excavation.
Considering that the same employer worked a surface of 181 m2 and the mass moved was 45.25 m3 with a weight of 1898 kg per cubic meter and an elevation of 4 dm, we can calculate the first part of the quantity of action equivalent to a day’s work. Thus, we have to multiply 1898 kg, the weight per cubic meter, and 45.25 times the number of m3. Hence, the first part of the daily quantity of action must be calculated by the multiplication of 1898 kg, the weight of 1 m3, 45.25 the number of m3, and 4 dm the height of each part of earth which raises its center of gravity; the product of these three quantities is equivalent to lifting 34.3 kg one kilometer. In addition, the weight of the excavator can be estimated in as approximately 1.7 kg. The quantity of action is then the same as lifting 43 kg one kilometer.
The following step is to calculate the quantity of action necessary to penetrate 25 cm of the soil in each swing. Previous experiences showed Coulomb that resistance was around 12 kg, but which in a good estimation can be increased to 15 kg. However, for the first swing 20 kg is a best approximation. Calculating the weight of earth as 6 kg, the quantity of swings per day as 14,316 and 25 cm the penetration of the excavator in each swing, while the force that a man uses to push the excavator is estimated as 15 kg. The product is then 53.6 kg lifted one kilometer. Adding the two quantities of actions one obtains in a day’s work 96.6 kg lifted one kilometer.
4.8. Conclusion
Coulomb remarks that all numerical findings for the quantity of action in the several kinds of work studied in the previous items are less than those used by the majority of authors. Nevertheless, the values were obtained from experience, almost all carried out by chosen men; the calculations were established on the basis of seven or eight hours of actual work.
According to Coulomb a man can in almost types of work carry out for some minutes a double or triple quantity of action of his average work. He can even do all his daily work in two or three hours.
He explains that the choice of men can significantly modify the value of the average force used. Coulomb also comments that he has followed for 10 years work with earth such as transportation, excavation, etc. Consequently, he has experience with diversified works with earth.
Finally, Coulomb emphasizes the importance of food and the weather in the results obtained in terms of quantity of action. The building works he did in Martinique compared with those in France were highly influenced by temperature. In places where men are subjected to high temperatures their quantities of action falls to one half or less in a day’s work.
5. Considerations on Coulomb’s sur la Force des Hommes
Coulomb is responsible for the introduction of economic studies in relation to machines and can be considered as a precursor of applied and industrial mechanics ( Oliveira, 2011 ). This task was done by mechanically measuring the human body as a kind of machine in order to economically measure a machine. The memoir Sur la Force des Hommes is an attempt to understand human work mechanically and is the first publication on physiology and ergonomics. Historically, the approach used by Coulomb to study the problem of fatigue with a mechanical model has an important meaning that is to consider the old question of how to measure human capacity to do a day’s work. His basic concern was to measure mean values of work in a day and not maximum or minimum values. In other words, Coulomb was looking for an actual measurement of work in a regular day’s work. Similarly, Frederik Winslow Taylor (1856-1915) made the same considerations and had the same concerns one century later. He became known as the father of production management and his method was characterized by the measurement of the flow of work required to achieve a higher degree of efficiency and productivity ( Vatin, 1999 ).
In 1821, Coulomb’s mechanical studies were published, including the memoir Sur la Force des Hommes. By introducing the question of human work as a machine operation, it was possible to study the work carried out by a machine economically. This double analogy created the conditions to construct the concepts of net work and global work applied to a given machine in order to measure its efficiency, costs, energy consumption, etc., providing the necessary theoretical tools to compare two different machines.
Sur la Force des Hommes should be considered a pioneering work in modern biomechanics, notwithstanding the many studies since antiquity, mainly addressed at the development of robotics in which it is attempted to reproduce the movement of animals and man. What in fact makes the difference in Coulomb’s memoir is the application of the concept of quantity of action (later called work) to obtain a mathematical model using the new tools of Rational Mechanics and differential calculus. This concept unifies the whole study and permits the comparison of different types of mechanical actions and machines including the human body. Coulomb’s memoir is a good handbook for civil and production engineering describing in detail several types of work with earth.
6. Final Remarks
Coulomb’s theory is based on an original conception of work, taking into account its duality: on the one hand, the effect produced by applying a system of forces to a machine; on the other, the fatigue to which a man would be submitted to produce that effect. From a general viewpoint, Coulomb’s above mentioned memoir was a fundamental reference about human work until the end of the nineteenth century. Its importance is based on three points:
1) Coulomb developed a systematic metrology, a methodology from which many results were obtained by some physiologists of work at beginning of the twentieth century, such as Jules Amar (1879-1935).
2) Coulomb’s memoir provided a theoretical matrix for “industrial mechanics”, a new discipline with a political vocation which emerged in the 1820s, whose main concern was to optimize machine efficiency, conceived of as a product of work in a similar way to human work.
3) Finally, the memoir is based on an original economic conceptualization which inspired at the end of the nineteenth century, by the well-known economist William Stanley Jevons (1835-1882), the founder of neoclassic theory in United Kingdom, who referred to Coulomb in his book: The theory of political economy (1871).
Cite this paper
Oliveira, A. R. E. (2016). Charles-Augustin Coulomb―The Founder of Physiology and Ergonomics. Advances in Historical Studies, 5, 207-222. http://dx.doi.org/10.4236/ahs.2016.55017
References
- 1. Carnot, L. (1803). Príncipes fondamentaux de l’équilibre et du mouvement, de l’imprimerie de Crapelet. [Paper reference 1]
- 2. Coulomb, C. A. (2002). Théorie des machines simples. Paris: Librairie Scientifique et Technique Albert Blanchard. [Paper reference 1]
- 3. Douglas, K. (2016). DNA Nanoscience: From Prebiotic Origins to Emerging Nanotechnology. Boca Raton, Florida: CRC Press. [Paper reference 1]
- 4. Lourtioz, J. M., & Lahmani, M. (2013). Nanoscience ad Nanotechnology: Evolution or Revolution? Berlin: Springer. [Paper reference 1]
- 5. Oliveira, A. R. E. (2011). Coriolis’ Theory of Machines and Mechanisms. Guanajuato, Mexico: IFToMM Congress. [Paper reference 1]
- 6. Oliveira, A. R. E. (2013). A History of the Work Concept: From Physics to Economics. Berlin: Springer. [Paper reference 1]
- 7. Oomens, C., & Brekelmans, M. (2009). Biomechanics: Concepts and Computation. Cambridge: Cambridge University Press.
http://dx.doi.org/10.1017/CBO9780511802720 [Paper reference 1] - 8. Rashed, R. (1998). Science a l’époque de la Revolution Francaise. Paris: Librairie Scientifique et Technique. [Paper reference 1]
- 9. Vatin, F. (1993). économie et Physique: 1780-1830. Paris: Presses universitaires de France. [Paper reference 1]
- 10. Vatin, F. (1998). économie Politique et économie Naturelle chez Antoine-Augustin Cournot. Paris: Presses Universitaires de France. [Paper reference 1]
- 11. Vatin, F. (1999). Le travail. Bruxelles: Sciences et Societé, Editions de l’Université de Bruxelles. [Paper reference 1]








