International Journal of Geosciences
Vol.06 No.12(2015), Article ID:61936,6 pages
10.4236/ijg.2015.612100
An Adaptive Approach of Satellite Baseline Estimation in InSAR
Xianghua Wang1,2
1School of Information Engineering, China University of Geosciences (Beijing), Beijing, China
2Academic Affairs Office, Minzu University of China, Beijing, China

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 24 September 2015; accepted 13 December 2015; published 16 December 2015

ABSTRACT
Baseline is an important parameter of radar interferometry. Generally, it can be estimated by satellite orbital data or ground control points. In this paper, an adaptive method is proposed to estimate it with combination satellite orbital data, and the accuracy of baseline estimated can be improved without ground control points; actual data of ERS and ENVISAT ASAR have been used in algorithm development and the final obtained elevation shows that the precise orbit data is more accurate than original orbit data in estimating baseline.
Keywords:
Baseline Estimation, Optimal Baseline, Adaptive Method, InSAR

1. Introduction
Interferometric Synthetic Aperture Radar (InSAR) technology has been used frequently to monitoring tiny land surface deformation in recent years. Land target elevation can be obtained from phase information carried by radar signal. Couple of single look complex views of the same area obtained from two antennas simultaneously or two parallel observations from one antenna are used to produce the interferometric image; the geometric relation of two antennas and the observed target make interferometry turning into the truth. Combination with the orbit and sensor parameters, more accurate and higher resolution elevation can be obtained.
As an important factor in InSAR, baseline is used to describe the spatial or temporal geometric relations between the two antennas and the slant range; the high-accuracy baseline can enhance interferometry of receiving signal, but poor-quality baseline will cause interference loss and lead to the low precise elevation evaluation. In this study, the optimal baseline is also used, and the result is verified by the ERS and ENVISAT ASAR data and shows good consistency with the observations.
2. InSAR Imaging Theory
In general, the spatial location of antennas was different in twice repetition while receiving signal from the same land target, here A1 and A2 represented the first position and second position, respectively. The difference between the two location produce the interference baseline vector, and here b represented its length, the angle with the horizon direction was represented by α, the horizontal and vertical component of b was represented by by and bz, respectively. The height difference between A1 and reference plane was represented by H, the height of land target T Was represented by h(y) and its slant range was represented by r, r + δ represented the slant range between A2 and land target T, all symbols are described in Figure 1.
Two complex images S1 and S2 were generated after processing echo signals of A1 and A2 using SAR tools, respectively. The interference image with dark and bright strips can be obtained after the operation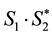 , here
, here  means the conjugation of S2. the phase of each pixel in interference image is in proportion to the distance difference δ and has constant ratio
means the conjugation of S2. the phase of each pixel in interference image is in proportion to the distance difference δ and has constant ratio 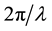 owing to the emission antenna is also echo receiver. in common, curvature of the earth can not be ignored in satellite-based processing. So the expressions concluded from Figure 1 are listed as follows [1] :
owing to the emission antenna is also echo receiver. in common, curvature of the earth can not be ignored in satellite-based processing. So the expressions concluded from Figure 1 are listed as follows [1] :
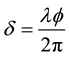 (1)
(1)
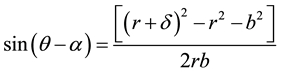 (2)
(2)
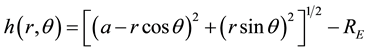 (3)
(3)
where 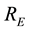 indicated the earth radius and
indicated the earth radius and 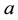 indicated the half of the major axis of satellite orbit, r means the slant range and is bound up with echo delay,
indicated the half of the major axis of satellite orbit, r means the slant range and is bound up with echo delay,  , b,
, b,  , r and H are known parameters, h,
, r and H are known parameters, h, 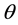 and
and 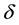 can be calculated by expression (1), (2) and (3) if given
can be calculated by expression (1), (2) and (3) if given 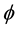 values.
values.
3. Optimal Baseline
As an important parameter in InSAR processing, baseline is defined as the line between the different locations of twice satellite repetition. Its accuracy can determine the accuracy of land target elevation. according to the theory of InSAR, the phase difference, wave length and baseline are the determinants of computing land target elevation, that is to say, the orbit parameters are necessary when calculating the elevation, and the information includes the position of satellite, baseline and its azimuth when satellite scanning the target.
As it is known, the more longer the spatial baseline is, the more weaker the interference of two images is, increasing the spatial baseline can increase the accuracy of elevation, but the increment of baseline has its limitation, and the limitation can be represented by 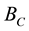 in the Equation (4).
in the Equation (4).
Figure 1. Geometry of InSAR.

where β represented the surface gradient and 


where






According to the error theory, 





where 
Where 



where W indicates the land target effective extension in one unit range lobe which is perpendicular to the direction of electromagnetic wave. 
Substitution Equations (6), (7), (8) and (9) to Equation (5), the estimated variance of land target height 

where 
Taking derivative to b in Equation (10) and making the derivation is equal to zero, then the optimal baseline can be computed by the following equation:

The Equation (11) shows that the optimal baseline will increase while wave frequency decreases.
4. Algorithm Development
4.1. Original Satellite Data
The satellite orbit can be expressed by position vector 












To resolving the position model, the amount





The position vector of satellite can be expressed by the following polynomial [6] :


The velocity vector can be obtained by taking differential to time t in polynomial (12), and velocity will keep consistency with position at given time. The velocity can be expressed as polynomial (13). Where 


4.2. Precise Orbit Data
The precise orbit data are provided by DEOS (Delft Institute for Earth-oriented Space Research), in which ERS-1, ERS-2 and ENVISAT ASAR are include. Running the program (getorb, version 2.2.0) provided by DEOS at given start time, step size and period, the geodetic or geocentric coordinates will be interpolated automatically after reading orbital data records, the program also can interpolate orbital profile every epoch and can print the UTC time, error, longitude, latitude, height of orbit (GRS80) and XYZ position values [7] .
Inputting the original orbit profile and precise orbit profile to program(getorb), then using polynomial fitting or linear interpolation to calculating the coefficient of orbit, transforming the original image coordinates to orbit coordinates according to the Doppler equation, then computing the baseline and comparing it with the optimal baseline, if the biases of baseline computed by precise orbit are less than the biases computed by original orbit data, the elevation will be computed by the baseline produced by precise orbit, otherwise, the original orbit data will be used.
5. Result and Discussion
In this paper, ERS-1 and ERS-2 are used to calculating the orbit equation firstly, then original orbit and precise orbit are used to compute the elevation. Table 1 and Table 2 show the orbit data and the precise satellite data, respectively. Table 3 shows the elevations computed by the orbit data. From Table 3, we can see that the accuracy of elevation obtained by precise orbit is better than that obtained by original data, and the relative error computed by precise data is smaller than the original. Meanwhile, the comparison is consistent with the result obtained by the optimal baseline; the results have been verified by ERS and ENVISAT and show the consistency;
Table 1. Original satellite data.
Table 2. Precise satellite data.
Table 3. Computed elevation.
it shows that the methodology used in the paper provides more accurate baseline estimation and can be an important reference for estimating baseline parameter.
Cite this paper
XianghuaWang,11, (2015) An Adaptive Approach of Satellite Baseline Estimation in InSAR. International Journal of Geosciences,06,1261-1266. doi: 10.4236/ijg.2015.612100
References
- 1. Yuan, X.K. (2003) Introduction to Spaceborne Synthetic Aperture Radar. National Defense Industry Press, Beijing.
- 2. Li, Z.H., Liu, N.J. and Xu, C.J. (2004) Error Analysis in InSAR Data Processing. Journal of Wuhan University—Information Science Edition, 29, 72-76.
- 3. Ruan, C.J., Xiang, J.B. and Wang, F. (2004) The Best Baseline Estimation of Spaceborne InSAR. Journal of Air Force Radar Academy, 18, 4-6.
- 4. de Rooi, J.J. and Eilers, P.H.C. (2012) Mixture Models for Baseline Estimation. Chemometrics and Intelligent Laboratory Systems, 117, 1-250. http://dx.doi.org/10.1016/j.chemolab.2011.11.001
- 5. Beaulne, P.D. and Sikaneta, I.C. (2005) A Simple and Precise Approach to Position and Velocity Estimation of Low Earth Orbit Satellites. Defence R&D Canada Technical Memorandum.
- 6. Hiroshi, K. and Masahiro, T. (1997) Baseline Estimation Using Ground Points for Interferometric SAR IGARSS'97, Proceedings. Vol. 1, Piscataway, NJ, Institute of Electrical and Electronics Engineers, Inc., 442-444.
- 7. Delft Institute of Earth Observation and Space Systems, Delft University of Technology, DORIS User’s Manual and Technical Documentation, December 2008.



