International Journal of Geosciences
Vol.06 No.08(2015), Article ID:58666,7 pages
10.4236/ijg.2015.68065
Spatial Variation of Soil Depth and Shallow Slope Failures in Sangun Mountains, Fukuoka Prefecture, Japan
Hendra Pachri, Yasuhiro Mitani, Hiro Ikemi, Wenxiao Jiang
Graduate School of Engineering, Kyushu University, Fukuoka, Japan
Email: hendra@doc.kyushu-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 June 2015; accepted 4 August 2015; published 7 August 2015
ABSTRACT
Shallow slope failure is often induced by rainfall infiltration in a soil mantle overlying a less permeable bedrock. Soil depth is an important input parameter in slope stability analysis. This paper provides the spatial variation of soil depth and the occurrence of slope failure in Sangun mountains area. The spatial pattern of soil depth was simulated by proses based model using airborne laser survey data (LiDAR data) and Geographic Information System (GIS) function. As a function for soil production, we use in the study area a numerical model developed by Dietrich et al. (1995) to predict the local spatial variation of the depth of soil. The soil depth data measured at 20 locations that represent morphological variability are used as a sample data set to test the model results. Furthermore, the soil depth variations are compared to the slope failure distribution in the whole area. Slope failure locations in the study area are identified from interpretation of aerial photographs and field surveys. Fifty-five of slope failures are considered for slope failure hazard analysis. Therefore, the slope failures occur more frequently at soil depth intervals in the ranged from 1.01 m to 1.5 m.
Keywords:
GIS, Sangun Mountains, Soil Depth, Slope Failures

1. Introduction
In the Sangun mountain, Fukuoka Prefecture, Japan, abundant slope failures occurred in 2003 [1] . Today, the assessment of the causes of slope failure occurrence is still conducted. There was no information about an influence on the type of soils on the occurrence. Moreover, in the slope stability analysis, soil thickness is an important input parameter. Shallow landsliding in soil-mantled landscapes can generate debris flows which scour low order channels, and deposit large quantities of sediment in higher order channels [2] . At the catchment scale, an active geomorphologic process is dominant, such as soil erosion and landsliding [3] .
The soil thickness on hillslope, which often coincides with the failure depth, is a critical parameter in performing a slope-instability analysis, and it is an important factor, such as to the ratio of the saturated depth to the soil thickness [4] . Soil thickness can vary as a function of many different and interplaying factors, such as underlying lithology, climate, gradient, hillslope curvature, upslope contribution area, and vegetation cover, making the distributed estimation of soil thickness challenging and often unreliable [3] . Soil is the surficial material mantling the underlying weathered or fresh bedrock and lacking relict rock structure (Dietrich et al., 1995). There are numerous researches that have analyzed the problem of soil thickness prediction (e.g., an empirical geomorphology-based approach [3] , a process based model using digital elevation data [5] , or a process-based terrain characterization [6] ). In this paper, we attempt to predict the soil depth values over a discrete space at a chosen spatial resolution. We simulate the soil depth by following the Dietrich model [5] . This is based on topographic Digital Elevation Data (DEM) using airbone laser survey data (LiDAR data) and Geographic Information System (GIS).
We have calibrated and validated the model in a study area, Sangun basin located in west part of Sangun mountains, Fukuoka Prefecture, Japan. Furthermore, the soil depth variations are compared to the slope failure distribution at whole area. Slope failure locations in the study area are identified from interpretation of aerial photographs and field surveys. There are fifty-five slope failures which are considered for slope failure hazard analysis.
2. Study Area
The Sangun mountains area is located in the north of Kyushu islands, Japan. The study area is the Sangun catchment area (1.67 km2) which is located the west part of Sangun mountains. Morphological characteristics of the study area present slope angle, aspect, and elevation. These characters were produced from DEM. It is characterized by rugged topography and steep slopes where the gradient varies from 10˚ to 70˚, moreover the majority of the aspect direction of slope is ranged from 150˚ to 337˚. The altitude of study area ranges between 290 and 930 m. The geology consists mainly of Mesozoic granitic rock. Granitic rocks are composed of a mixture of quartz, feldspar, micas and ferromagnesium minerals. On July 18-19, 2003, a short duration, high-intensity rainfall event impacted the Sangun city area (Figure 1). Triggering many landslides and debris flows [1] .
The slope failures and resultant debris flows were the largest and most damaging of these disasters. A moderate-size, 3 - 10 m deep debris avalanche triggered the debris flow which caused casualties. The rainfall intensity was estimated to about 315 mm/day, and the density of slope failure was about 48 points/km2.
3. Methodology
3.1. A Concept of Soil Depth Modelling
In order to create the patch variation in soil depth we use a stochastic soil production and annual soil transport model, building upon earlier work [5] . The simple model for soil depth was proposed to explain the general tendency in hilly landscapes for the sharp convex ridges to have thin soil or bedrock outcrop. Their model had explored two general kinds of production laws, one which is a simple exponential decline with thickening soil, i.e., 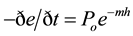 (in which Po and m are empirical constants). In the model, K and ρs were assumed spatially constant with the soil depth described as a complex, bell-shaped function of h,
(in which Po and m are empirical constants). In the model, K and ρs were assumed spatially constant with the soil depth described as a complex, bell-shaped function of h,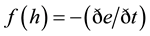 :
:
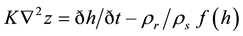 (1)
(1)
where ρr and ρs are the bulk density of rock and soil. The soil depth model in the form given in Equation (1) assumes that over the time period sufficient to influence the soil depth, the dominant hillslope transport process can be represented by a slope-dependent transport law.
3.2. Data Preparation
To apply Equation (1) to Sangun basin, we need to assign the diffusivity (K) value, the production function, and
Figure 1. Sangun basin boundary and small studied catchment in the upstream part which have been selected for soil depth investigations.
the bedrock and soil density. The diffusivity is not known, therefore the simulation of soil depth must consider the change of the diffusivity (K) values to get the reasonable value. Here we will use the range 37 - 55 cm2/yr. The production function is based on of the production rate of cosmogenic nuclides concentration. Moreover, the bedrock and soil density were obtained from the literature. We use a 5 m resolution Digital Elevation Model (DEM) prepared using airborne laser survey data (LiDAR data). An inventory of slope failure has been documented. The distribution of the slope failure has been conducted by utilizing Geographic Information System (GIS) function.
3.3. Simulation Process
The soil depth model simulations were carried out by utilizing Geographic Information System (GIS) function. The soil model, in the form given in Equation (1), assumes that over the time period sufficient to influence the soil depth, the dominant hillslope process can be represented by a slope dependent transport law. The diffusivity (K), the bedrock and soil density, and the production function are uncertainty values. Therefore, we needed guidance for initial values from literature. Dietrich et al. [5] explained that diffusivity (K) value was estimated by Reneau (1988) by using Equation (1) by dividing a calculated flux of sediment required to in-fill unchannelled valleys (based on radiocarbon determined deposition rates) by the mean gradient of the adjacent source slopes.
Therefore, here we will use 50 cm2/yr. Moreover, for the bedrock and soil density ratio we will use the value proposed by Dietrich, et.al data of about 1.7. Furthermore, the production function is not known, therefore the initial value will be as from Dietrich, et.al data, and we make a range of values to get the best results from simulations. The range value of 0.019 cm/yr to 0.025 cm/yr will be used in the simulation. By fitting an exponential function, 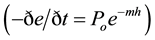 , to the thick (no production at 150 cm) and thin soil production rates (0.0042 cm/yr at 30 cm), the Po = 0.019 cm/yr and m = 0.05 [5] values are obtained. During one simulation, the time step will be set up to 1000 years and a time limit of 2000 yr.
, to the thick (no production at 150 cm) and thin soil production rates (0.0042 cm/yr at 30 cm), the Po = 0.019 cm/yr and m = 0.05 [5] values are obtained. During one simulation, the time step will be set up to 1000 years and a time limit of 2000 yr.
4. Results and Model Comparison
4.1. Soil Depth Investigation
We apply these models to a small catchment in the upper Sangun mountain area. The area is mostly underlain by granite rock. In the investigation, the morphometry aspect was considered to collect measurements of soil depth. We have two profile of soil investigation. A Portable Dinamic Cone-Penetrometer Test (CPT) tool was used in the measurements. The CPT is a valuable method of assessing subsurface stratigraphy associated with soft materials, discontinuous lenses, organic materials (peat), potentially liquefiable materials (silt, sands, and granule gravel), and landslides [7] . The measurements were carried out at 20 selected points, see Figure 1. The sampling interval was 5 or 10 m, and positions were identified by a GPS.
In order to determine the grade of weathering, the classification of granites presented by Hencher and Martin [8] was selected. This classification makes possible to classify weathering grade according to characterized with a range of rebound values of the N-type of hammer. The resulting classification of selected parts in Sangun Mountain is given in Table 1.
4.2. Soil Depth Simulation
This simulation presents a distribution of soil depth. The variables identified as predictors include topographic variables, soil production rate (Po), a density of the rock and soil, and diffusivity (K) value. However, the range of soil production rate (Po) was considered in the simulation such to get a reasonable value of soil depth comparable with soil depth in direct measurements.
We use three Po values, such as 0.019, 0.022, and 0.025 cm/yr. For the purpose of model validation, the time interval of 1000 to 2000 years was used. Figure 2 shows soil depth distribution maps with importance value of the Po value, (a) 0.019 cm/yr, (b) 0.022 cm/yr, and (c) 0.025 cm/yr.
4.3. Model Validation
The performance of the process based model can be compared to the field measurements to compute the error between the two data sets. We propose that mean square prediction error close to zero value could indicate a good result from simulation process. Root Mean Square Error (RMSE) (also known as Root Mean Square Deviation) is one of the most widely used statistics in GIS. In a variety of geostatistical applications, RMSE is one method to evaluate the model performance.
Root mean square error takes the difference for each soil depth value based on simulation and surveyed value. We can swap the order of subtraction because the next step is to take the square of the difference. RMSE value is calculated by following Equation (2):
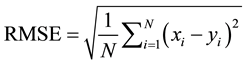 (2)
(2)
Table 1. Soil depth (m) measurement in the upstream part of Sangun catchment, Fukuoka Prefecture (2015).
Figure 2. Spatial distribution of soil depth based on simulation of the soil production rate (Po).
where N: number of observation points; xi: prediction value; yi: observation value. The raster file of soil depth was prepared and sampled at the measuring points. Therefore, we estimate the soil characteristic and compared the observed and predicted soil depth values (Table 1). The characteristic soil depth was divided in two parts depending on the N value. N value 30 represents the moderately weathered rock zone, and 50 represents the slightly weathered rock zone.
The process based model simulates soil depth at 11 times (1000; 1100; 1200; 1300; 1400; 1500; 1600; 1700; 1800; 1900; and 2000) and have Po values 0.019; 0.022; and 0.025 cm/yr for simulating the influence of soil production rate. Observations were available only for twenty observation points. Figure 3 shows that the model performed very well for simulating soil depth. In the Figure 3(a) shows the N value 30 which a blue line presents Po = 0.019 cm/yr and time 1500 year are the better RMSE value (0.306) than other Po values.
Furthermore, Figure 3(b) shows the N value 50 which a red line presents soil Po = 0.019 cm/yr and time 2000 year have a low RMSE value (0.570). Therefore, the root-mean-square errors (RMSE) reported in Figure 3 indicate that the RMSE value 0.306 is better than the other values the process based model for predicting soil depth at the point scale in term of these the sample statistical measures.
5. Discussions
5.1. Soil Depth Distribution
Process based model [5] has been used to predict soil depth over a landscape using topographic and, soil production rate and time in the Sangun mountains. The variables identified as predictors included morphology, soil

Figure 3. Root Mean Square Error (RMSE) values on validation. (a) N value = 30; and (b) N value = 50.
depth observations, soil production rate (Po), and production time (year). In this study, the soil production rate (Po) 0.019 cm/yr, 1500 year, N value 30 (0.1 - 1.6 m) provide the reasonable model for spatial distribution of soil depth. Table 2 shows an amount of soil depth distribution area in the study area that based on the simulation by using the N value 30 (0.1 - 1.6 m) and the varying of the soil production rate (Po). The relationship between soil production rate (Po) and the amount of soil depth distribution is not linear. The soil production rate increases for soil depth 0.51 - 1.00 m. Moreover, the soil depths of 0 - 0.5 m, and greater than 1.01 m show the soil production rate (Po) to decrease. In the soil depth model the distribution of soil depth shows a trend with a peak centered on the depth range 0.51 - 1.00 m (Figure 4). For Po = 0.019 cm/yr, the maximum area of soil depth distribution is 0.875 km2 the 1500 years. Secondly, the Po = 0.022 cm/yr shows the peak maximum area is 0.928 km2 the 1300 years. And thirdly, the Po = 0.025 cm/yr shows the peak maximum area is 1.011 km2 on 1100 years. Furthermore, the area of distribution of soil depth 0.51 - 1.00 m is larger than the other soil depth interval, about 52.23% of the total area.
5.2. Relationship between Soil Depth and Distribution of Slope Failures
Figure 4 shows the location of Sangun mountain where a significant number of slope failures occurred when Typhoon hit on June 2003. The catchment area is 1.67 km2 with an average slope angle of 36.5˚. Table 2 shows the number of slope failures based on the distribution of soil depth. Soil depth range from 0.51 - 1.00 m has the largest number of slope failures (28 locations). Moreover, a density of slope failures is calculated by comparison of a percentage of the number of slope failure and a percentage of the area of soil depth distributions. As shown in Table 2, a frequency ratio (FR) of slope failure and soil depth distribution was calculated, as a density of slope failure. The slope failures occur in the soil depth range from 0 m to 2 m. The soil depth range from 1.0 m to 1.5 m has higher than the other of soil depth intervals. The frequency ratio value of this density is 1.37.
Landslide occurrence in tropical and sub-tropical region is generally associated with weathered rock profile characterized by chemical and mineralogical heterogeneities [9] . Although, we did not carry out the laboratory test of a mineral composition of the soil, we assume that the occurrence of feldspars play a role in the occurrence of rock weathering and produce of soil layer. Feldspars are susceptible to both chemical and physical weathering, breaking down into clays. The feldspar content of granitic rocks is commonly in the 30% to 80% range. Feldspars can be further broken into two groups-plagioclase and alkali feldspars. Plagioclase is a solid solution series of calcic to sodic feldspars (anorthite is the calcic end-member, albite is the sodic end-member). Furthermore, a rainfall followed by rock type is one of parameter influencing the weathering process, which leads to the formation of slope failure as the present one.
Figure 4. Graph of distribution of soil depth based on soil production rate (Po) values during simulation.
Table 2. Soil depth distribution in the upper part of Sangun basin based on the simulation for N value = 30.
6. Conclusion
In this study, the spatial distribution of soil depth was estimated using a process based model [5] and different soil depth observations to perform a simulation analysis to provide the relationship of slope failure and soil depth distribution in the upper catchment of Sangun mountains. Results from the simulation analysis indicated that topographic variables, soil production rate (Po), and a soil production time (year) provided the reasonable model for spatial distribution of soil depth. The results also showed that the soil depth ranged from 0.51 m to 1 m had the largest area of soil distribution, and that the high density of slope failures was occurring at the soil depth ranged from 1 m to 1.5 m. Considering the limited number of soil depth observations, this model appears as an important improvement toward solving the need for distributed soil depth information in the process based modeling.
Acknowledgements
The authors would like to thank the Indonesian Government, Directorate General of Higher Education for its DIKTI Scholarship. This work was supported by JSPS KAKENHI Grant Number 25350429.
Cite this paper
HendraPachri,YasuhiroMitani,HiroIkemi,WenxiaoJiang, (2015) Spatial Variation of Soil Depth and Shallow Slope Failures in Sangun Mountains, Fukuoka Prefecture, Japan. International Journal of Geosciences,06,813-820. doi: 10.4236/ijg.2015.68065
References
- 1. Hanamura, et al. (2004) Heavy Rain Disaster in Kyushu Area on July 2003. Japan Society of Engineering Geology, 25, 30-31.
- 2. Costa, J.E. and Wieczorek, G.F. (1987) Debris flow/Avalanches: Process, Recognition and Mitigation. Reviews in Engineering Geology, 7, 239 p.
- 3. Catani, F., Segoni, S. and Falorni, G. (2010) An Empirical Geomorphology-Based Approach to the Spatial Prediction of Soil Thickness at Cathment Scale. Water Resources Research, 46, W05508.
http://dx.doi.org/10.1029/2008WR007450 - 4. Ho, J.Y., Tun Lee, K., Chang. T.C., Wang, Z.Y. and Liao, Y.H. (2012) Influences of Spatial Distribution of Soil Thickness on Shallow Landslide Prediction. Engineering Geology, 124, 38-46.
http://dx.doi.org/10.1016/j.enggeo.2011.09.013 - 5. Dietrich, W.E., Reiss, R., Hus. M.L. and Montgomery, D.R. (1995) A Process-Based Model for Colluvial Soil Depth and Shallow Landsliding Using Digital Elevation Data. Hydrological Processes, 9, 383-400. http://dx.doi.org/10.1002/hyp.3360090311
- 6. Park, S.J., McSweeney, K. and Lowery, B. (2001) Identification of the Spatial Distribution of Soils Using a Process-Based Terrain Characterization. Geoderma, 103, 249-272.
http://dx.doi.org/10.1016/S0016-7061(01)00042-8 - 7. David, R. (2006) Subsurface Exploration Using the Standard Penetration Test and the Cone Penetrometer Test. Environmental & Engineering Geoscience, XII, 161-179.
- 8. Vahed, G, Husaini, O. and Bujang, K.H. (2009) A Study of the Weathering of the Seremban Granite. Electronic Journal of Geotechnical Engineering, 14.
- 9. Duzgoren-Aydin, NS. and Aydin, A. (2006) Chemical and Mineralogical Heterogeneities of Weathered Profiles: Implications for Landslide Investigation. Natural Hazards and Earth System Sciences, 6, 315-322. http://dx.doi.org/10.5194/nhess-6-315-2006





