International Journal of Geosciences
Vol.5 No.3(2014), Article ID:44217,8 pages DOI:10.4236/ijg.2014.53025
Study of the Effects of Atmospheric Pressure in the Time Series of Muon Detector Using the Method of Spectral Analysis
Nivaor Rodolfo Rigozo
Instituto Nacional de Pesquisas Espaciais (INPE), São José dos Campos, Brazil
Email: nivaor.rigozo@inpe.br
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 18 January 2014; revised 25 February 2014; accepted 11 March 2014
ABSTRACT
This paper presented a study of the effects of atmospheric pressure in the time series of muon detector using the method of spectral analysis of iterative regression. In which it observed that the periods of 4.8, 5.7, 7.0, 8.7, 10.7, 14.1, 16.2, 21.0, 31.2 and 356.7 days present in the amplitude spectrum of atmospheric pressure are also present in the amplitude spectra of muons data. Also it observed that the standardization of muons data to eliminate the effects of atmospheric pressure is efficient for periods under 7 days.
Keywords:Cosmic Rays; Time Series; Spectral Analysis

1. Introduction
The concern of the study of space weather is to collect data of phenomena from the Sun and the Earth’s magnetosphere, so that one can make a prediction of these phenomena before they occur and understand the physical phenomena generated in the Sun and its consequences in the interplanetary medium and especially on planet Earth. Among the main solar phenomena, the Coronal Mass Ejections (CMEs) are the main causes of intense magnetic storms on Earth [1] [2] .
CMEs are eruptions of plasma from the solar atmosphere involving regions of closed field lines that are ejected in the interplanetary medium. Such regions, and the shocks that they can generate, have pronounced effects on the density of cosmic rays both locally and at a distance. These effects on energetic particles can often be used to identify CMEs in the interplanetary medium, where they are called “ejecta” [3] . The importance of using the components of the cosmic rays is secondary as “informants” of the presence of CMEs toward Earth. The cosmic rays travel with the speed of light in the Earth direction faster than the CMEs, which enables determination beforehand of the occurrence of a geomagnetic storm.
One of the secondary components of cosmic rays is muons. They are high-energy particles originating from the interaction of high-energy protons from cosmic radiation in the Earth’s atmosphere. Its formation and propagation in the atmosphere depend on the atmospheric pressure and temperature. According to Reference [4] , the daily variations of cosmic radiation are caused by atmospheric variations. Thus, the effects of temperature and pressure represent the main interference in the study of the variations of intensity of the primary cosmic radiation. The variations in air masses produce changes in the flux of cosmic rays entering the detector [5] [6] . Due to this effect, what one does is a correction of the atmospheric effects (pressure and temperature) on the data of cosmic rays [7] . This correction or standardization removes atmospheric effects (pressure and temperature) by the equation:
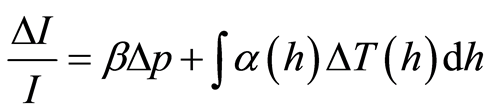 (1)
(1)
where Dp is the change in atmospheric pressure and DT is the temperature variation with altitude h. The first term of the equation represents the barometric effect, and where β is the barometric coefficient. The second term of the equation represents the temperature effects, where α is the temperature coefficient that depends on the altitude [8] .
This paper presents a study of muon time series (2006-2010) through the spectral analysis of iterative regression method in order to verify that Equation (1) is actually removing the atmospheric effects in muon data.
2. Method
2.1. Data Setting
The data used in the secondary component of cosmic rays (muons) were measured by muon telescope scintillator installed in São Martinho da Serra-Brasil (29.3˚S, 53.5˚O, magnetic rigidity of 14 GV), in the Southern Space Observatory-SSO/CRSPE/INPE, financed by NSF-National Science Foundation of the United States, by Bartol Institute (Newark), the University of Nagoya in Japan, and the Brazilian government.
The muons and pressure time series used starting at 1 December 2006 to 18 September 2010. In this study only the daily averages of the raw data (Figure 1) and standardized data by Equation (1) (Figure 2) to the Vertical (V), North (N), South (S), East (L) and West (W) direction (or channels).
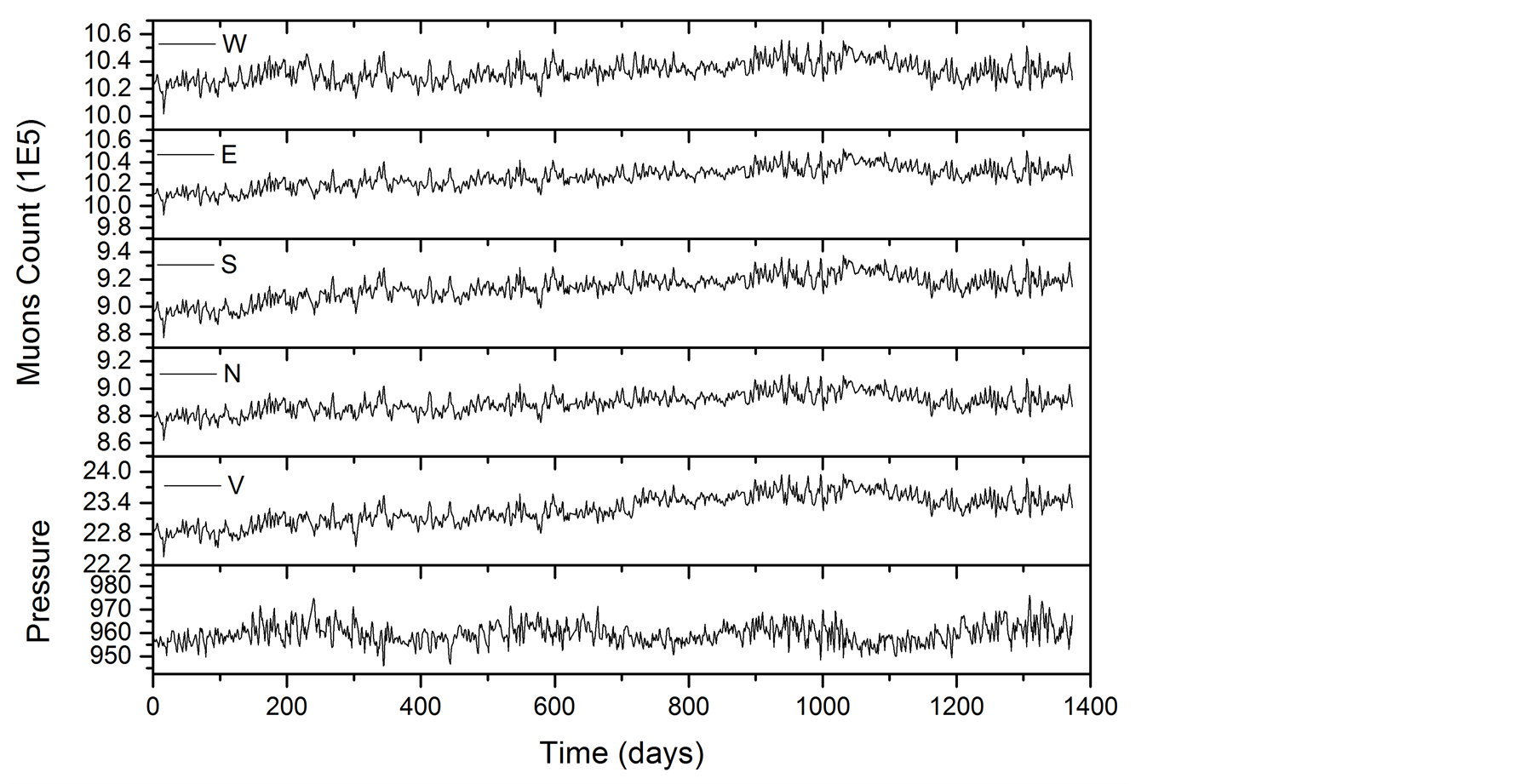
Figure 1. The muon daily average time series (not standardized) for V, N, S, E, W channels and pressure daily average time series to time interval of 2006 to 2010.
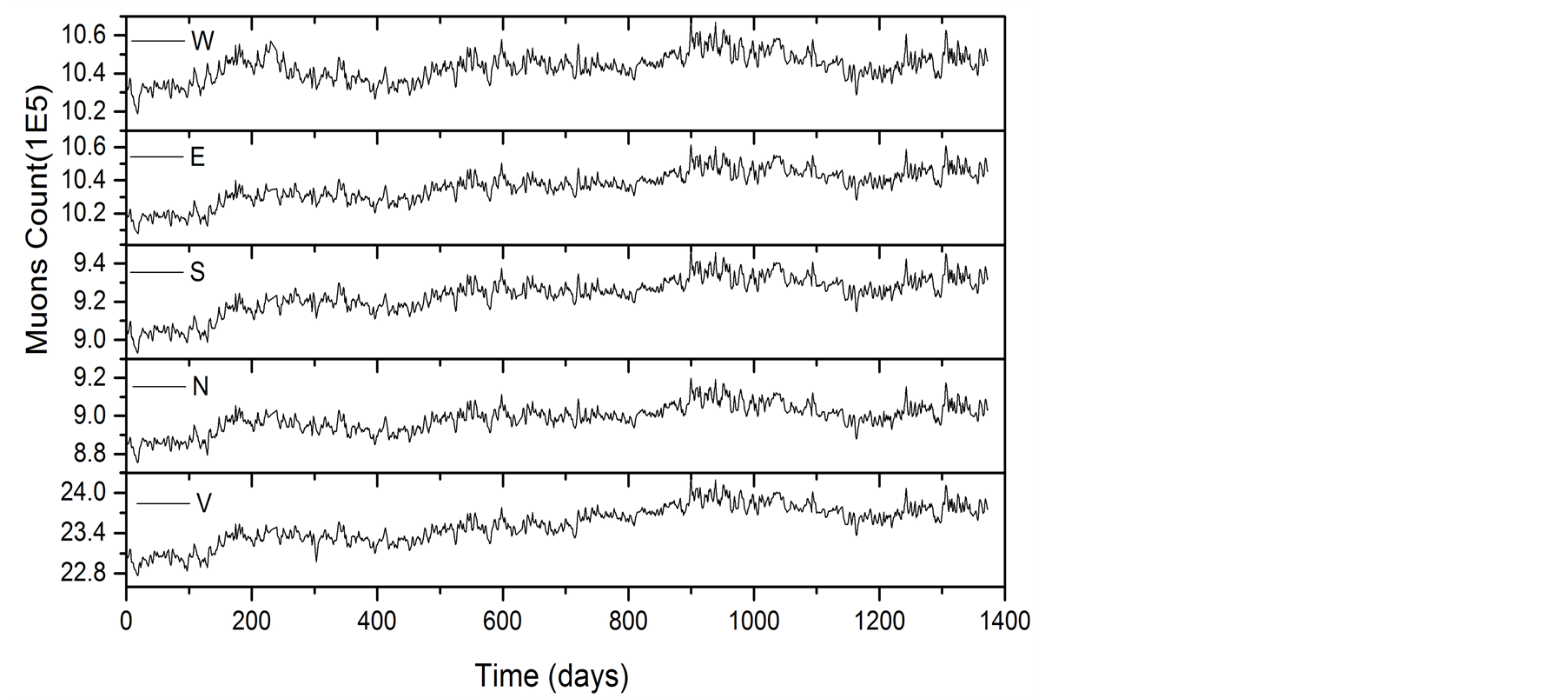
Figure 2. Muons standardized daily average time series for V, N, S, E, W channels to time interval 2006 to 2010.
2.2. Iterative Spectral Analysis
In this study the spectral analysis was used by iterative regression in the search for periodicities present in the muon and pressure time series, was described in its general form by Reference [9] and Reference [10] . It may be applied to the fit of any function (derivable on regard to variables and parameters) to experimental or observational data, without need of previous linearization. For reason of processing time in most computers, the number of parameters and variables cannot be too high but there is not such practical limit for the number of data points which in principle must not be equidistant. It is applied, in this work, to searching periodicities in time series, with the use, for every period searched, of a unique sine function with three unknown parameters, a0 = amplitude, a1 = angular frequency, and a2 = phase and only one variable, t = time. The values for the three unknown parameter are determined one at a time by iteration on the original time series with the specific condition of restricting the angular frequency to a narrow domain around its expected value. The starting point of the method is the definition of a so-called conditional function, which is:
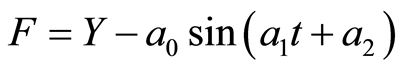 (2)
(2)
where Y is the observed signal, t is the time that the conditional function F represents, for every experimental point, the difference between the observed value Y and the fit curve for the corresponding abscissa.
As the method is iterative, for every iteration, the corrective terms A0, A1 and A2 are calculated. They will be applied to the parameters a0, a1 and a2, respectively. The corrective terms represent the solutions of the linear system of equation:
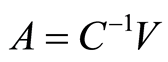 (3)
(3)
where terms Cij and Vi, of matrixes C and V, are the sums for all experimental points of actualized values (for every iteration) of the right hand expression:
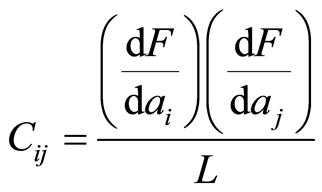 (4)
(4)
 (5)
(5)
(in order to simplify, according to usual practice, sum symbols are omitted)
with
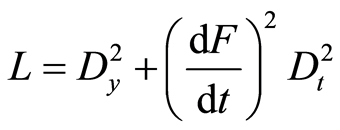 (6)
(6)
L is the weighing coefficient, for every experimental point. DY and Dt represent the standard deviation or error, associated to Y and t, respectively.
Corrective terms A0, A1 and A2 are applied to parameters a0, a1 and a2, as follow:
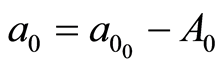 (7)
(7)
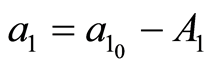 (8)
(8)
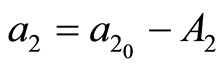 (9)
(9)
where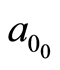 ,
, 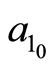 ,
, 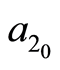 represent initial values, every iteration. These values may be arbitrarily chosen. However, to save processing time, they are chosen close to the expected values.
represent initial values, every iteration. These values may be arbitrarily chosen. However, to save processing time, they are chosen close to the expected values.
The determination of the unknown parameters ai must respect a convergence criterion. Iteration are done up to when the sum of squared values of Ai turn to be lower than a given value. When this convergence criterion is reached, the values of parameters ai are considered as being the best estimates. Their standard deviations 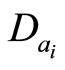 are given by:
are given by:
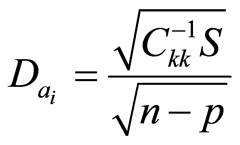 (10)
(10)
where Ckk is the diagonal term diagonal of matrix C−1, n is the number of experimental data, p is the number of unknown parameters and S is defined as the sum, for all experimental points, of the squared residues F defined in Equation (2) and weighed by coefficients L:
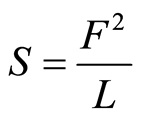 . (11)
. (11)
The program performs, successively, the search for sine function parameter values through a sweep of possible angular frequency values. Also to save processing time it may be recommended to restrict the search to frequency domains where amplitude peak are expected after applying one of the above described methods. The allowed variation of angular frequency for every periodicity research is:
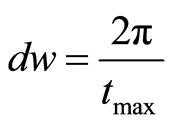 (12)
(12)
where tmax= tfinal − tinicial .
The maximum angular frequency is:
 , (13)
, (13)
where N is the number of data points.
This maximum angular frequency corresponds to the maximum allowed frequency called Nyquist frequency which is expressed by:
3. Results and Discussion
The muons time series have a high correlation between the channels of 0.88 to 0.98 for the raw data and standardized data. Representing that the channels are responding the same way for possible variations tails by physical phenomena, thus, it is expected that the spectral analysis of each channel have almost the same results.
Figure 3 shows the amplitude spectrum of the time series of atmospheric pressure and muons (no-standardized) for V, N, S, E and W channels with confidence levels 66% and 95%. As expected the spectra of each channel showed no significant differences. In Figure 3 shows some selected frequencies (lines in red and blue) for better viewing and discussion of results.
The periodicities of 4.8, 5.7, 7.0, 8.7, 10.7, 14.1, 16.2, 21.0, 31.2, 356.7 days, highlighted by the red line represent the periodicities found in the atmospheric pressure time series, with a confidence level above 95%, and
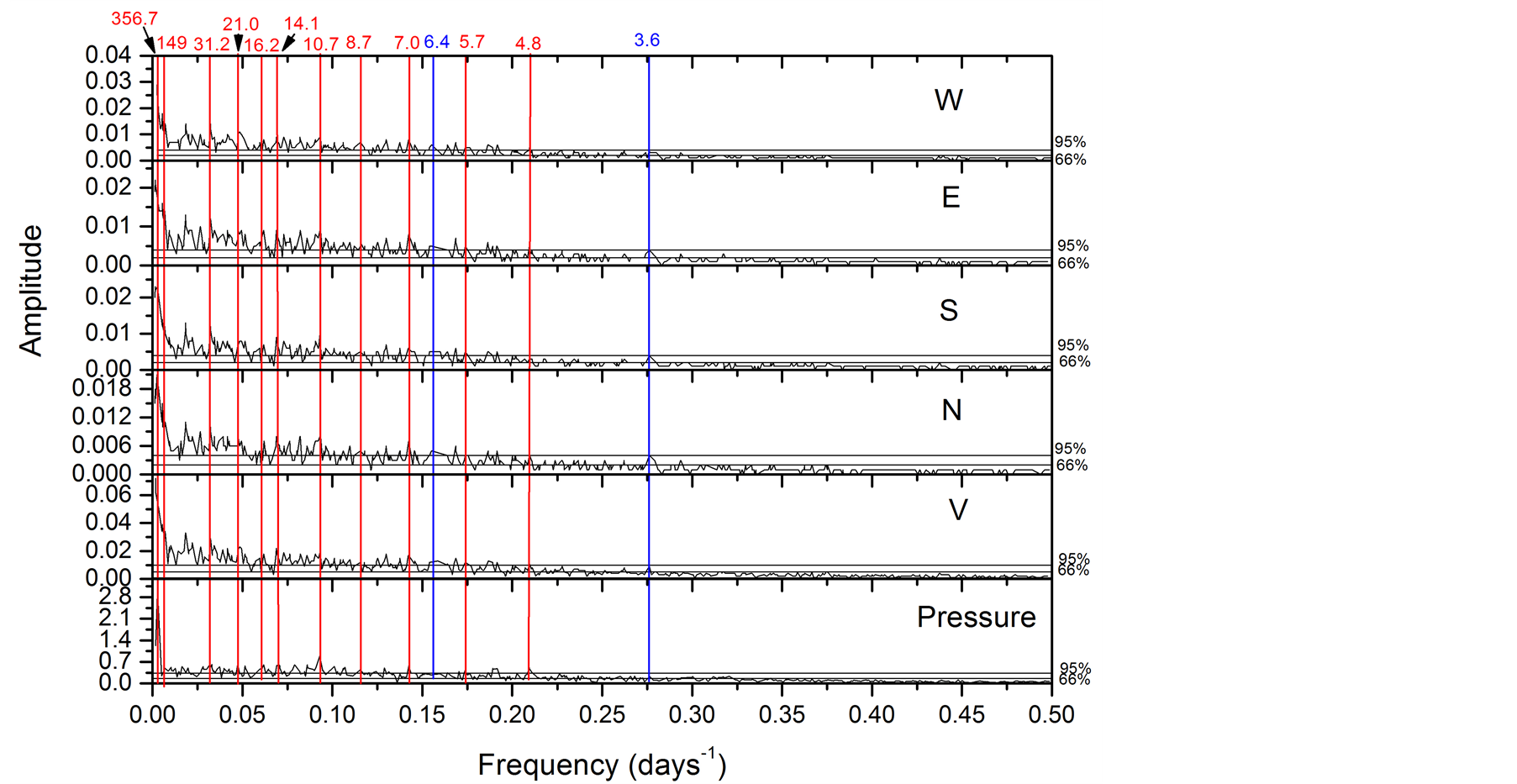
Figure 3. Amplitude spectrum by muons (non-standardized) and pressure time series.
that are also present in muon raw time series for all channels.
The correlation coefficients (r) of the reconstruction of periodic signals found in atmospheric pressure and muon (for all channels) time series are presented in Table 1. It is observed that both series have a negative correlation, that is, when an increase in air pressure occurs a decrease in the detection of muons for all channels occurs. It just did not go for the period of 356.7 days, in which we observed a positive correlation to channels. One hypothesis to explain this positive correlation between atmospheric pressure and the muons data is that annual variation in pressure may be due to orbital parameters (translational motion of the Earth) and not atmospheric.
The periodicities of 3.6 and 6.4 days, highlighted by blue lines, represent the periodicities found in the muons data, with a confidence level above 95%, but that was not observed in the atmospheric pressure time series of with a significant level of confidence.
Figure 4 shows the amplitude spectrum of the time series of atmospheric pressure and muons standardized for V, N, S, E and W channels to confidence levels 66% and 95% data. Here also no significant differences in the spectra were observed for each channel.
Comparing these periodicities found in muons raw data (Figure 3) with the periodicities found in muons standardized (Figure 4) some differences were observed between them:
1) It is clear that standardization makes a filter in the muons data, and eliminating certain frequencies;
2) The elimination of the effects of atmospheric pressure through muons standardized data is really effective for periods below 7 days only;
3) To periodicities longer than 7 days, only the period of 8.7, 16.2 and 21.0 were eliminated by standardizing pressure;
4) The periodicities of 3.6 and 6.4 days, highlighted by blue lines, that do not match the atmospheric variations were eliminated muon data for all channels. This implies that standardization may be eliminating possible physical phenomena that are not atmospheric effects.
This article presents a way to make the elimination of the effects of atmospheric pressure more efficient in the muon data, that is: 1) Identify all frequencies that are due to the influence of atmospheric pressure; 2) Reconstruct this dependency (periodicities) in the muons data; 3) Subtract this reconstruction in the muons time series. Thus we obtain a muons time series more purified to the atmospheric pressure effects.
The Reference [11] have analyzed the cosmic-ray muons intensity record from Belgrade muons detectors in period 2002-2004, they have found periodicities of 1, 5.3, 8.7, 13.6, 20.5, 26.5, 34.5, 37, 57, 77, 90, 162, 194, 236, 350 days. They identified the atmospheric effects to 1 days, and solar rotation period (~26.5 days) and yours harmonics (13.6 and 8.7 days), well as evidence of signals between 3.5 and 5.3 days attributed both to the
Table 1. Correlation coefficient of frequency of the atmospheric pressure data and muons raw data for V, N, S, E and W channels.
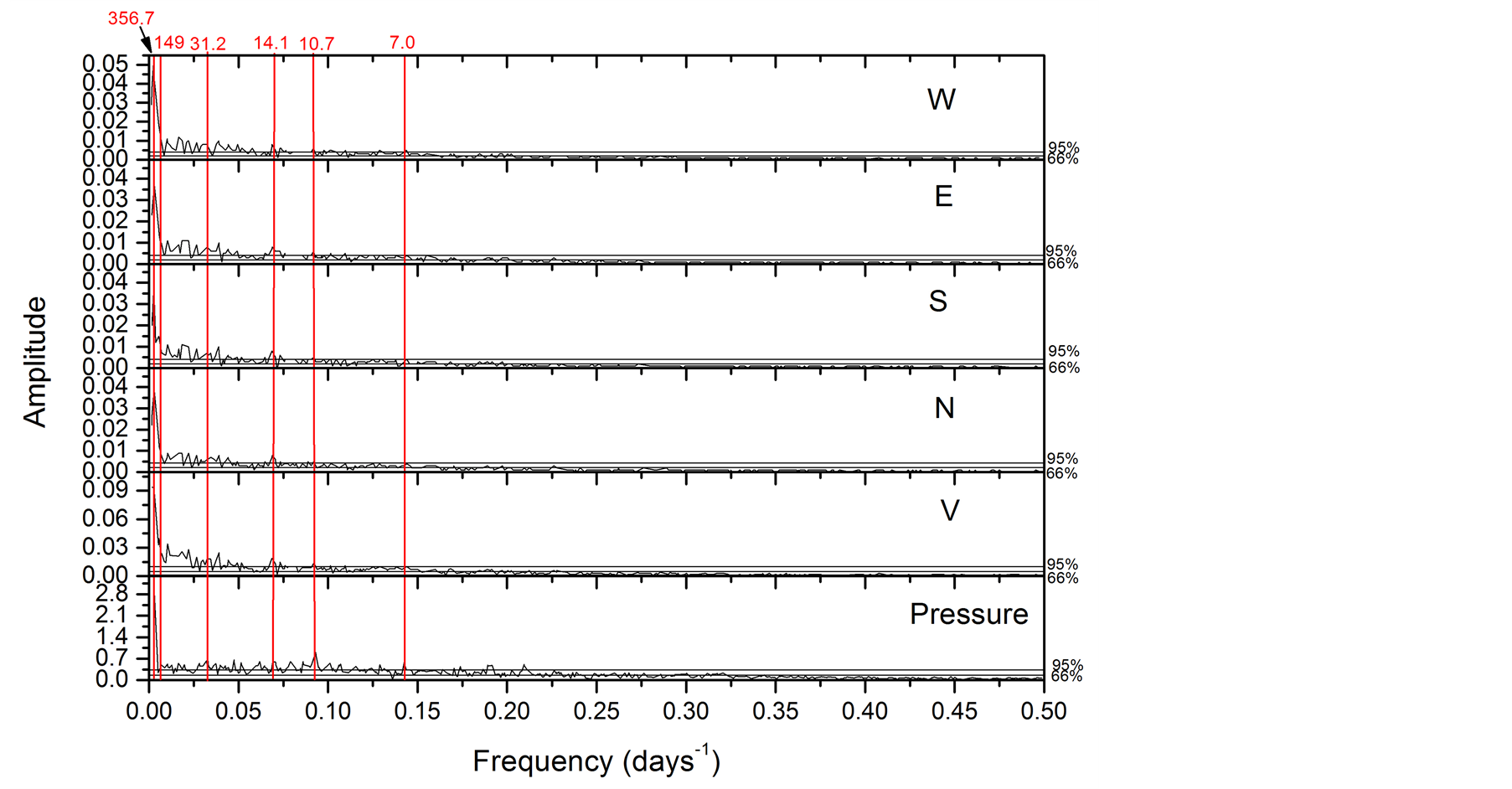
Figure 4. Amplitude spectrum of muons standardized and pressure time series.
high harmonics of the solar rotation period. They also found periodicities of 20.5 and 90 days in which failed to assign any physical phenomenon for this. The results obtained by Reference [11] are partly in accordance with the results obtained in this work. In which it is evident that the standardizing pressure eliminating possible physical phenomena that are not atmospheric effects, for periods between 3.5 and 5.3 - 6.4 days. While the periodicity of 20.5 days they found is atmospheric pressure effect as shown in this work. Has a period of 8.7 years as they presented harmonious solar rotation is really the atmospheric pressure effect, the harmonic of the solar rotation would be between 6.4 - 6.7 days, this period finding of this work and it was eliminated by standardizing pressure effect, what is not.
The cosmic radiation intensity is not constant, it continually varies for different time scales. Its flow incident on the Earth’s atmosphere is basically modulated by three processes: 1) Variations of the solar wind within the heliosphere (with time scale 10 to 1,000 years); 2) Variations of the Earth’s magnetic field (100 - 10,000 years); 3) Variations of the interstellar flow outside the heliosphere (>106 years) [12] . Variations with short periods of time and with a terrestrial origin are called seasonal and diurnal variations, caused by differences in the Earth’s atmospheric structure between the winter and summer seasons, and between the day and night [13] -[15] . Other variation of the cosmic radiation, with a climatic origin, but with glacial periods, is due to orbital parameters. Though this mechanism is still not yet proven, it demonstrates the cosmic radiation variations with 100,000 year-cyclicity. Other mechanismsmay be associated to the geodynamo’s orbital modulation, therefore, modulating the intensity and direction of the geomagnetic field, and/or the correlations of orbital parameters with the solar wind in the heliosphere [12] .
4. Conclusions
This paper presented a study of the effects of atmospheric pressure time series in the muon detector by spectral analysis using the iterative regression method. It was verified that Equation (1) effectively eliminates the effects of atmospheric pressure to periods below of 7 days only. In which it was determined that the periods of 4.8, 5.7, 7.0, 8.7, 10.7, 14.1, 16.2, 21.0, 31.2, and 356.7 days pertaining to atmospheric pressure are present in the muon data, both in the raw as the standardized (by Equation (1)) time series.
It was also determined that standardization may be eliminating other signs, which are not due to the effects of atmospheric pressure, as observed periods of 3.6 and 6.4 days. In this work, it was shown that the period of 356.7 days presented a positive correlation between two time series. The periodicities which are smaller than the 356.7 days show a negative correlation.
For a complete study, proposal was presented to make the elimination of the atmospheric pressure effects more efficient in the muons time series.
Acknowledgements
The author wish to thanks to CNPq by financial support: N. R. Rigozo-CNPq (APQ 470605/2012-0 and research productivity, 303368/2012-8).
References
- Gosling, J.T., Bame, S.J., McComas, D.J. and Phillips, J.L. (1990) Coronal Mass Ejections and Large Geomagnetic Storms. Geophysical Research Letters, 17, 901-904. http://dx.doi.org/10.1029/GL017i007p00901
- Gosling, J.T., McComas, D.J., Phillips, J.L. andBame, S.J. (1991) Geomagnetic Activity Associated with Earth Passage of Interplanetary Shock Disturbances and Coronal Mass Ejections. Journal of Geophysical Research, 96, 7831- 7838. http://dx.doi.org/10.1029/91JA00316
- Cane, H.V. (2000) Coronalmass Ejections and Forbush Decreases. Space Science Reviews, 93, 55-77. http://dx.doi.org/10.1023/A:1026532125747
- Pomerantz, M.A. and Duggal, S.P. (1971) The Cosmic Ray Solar Diurnal Anisotropy. Space Science Reviews, 12, 75- 130. http://dx.doi.org/10.1007/BF00172130
- Simpson, J.A., Fonger, W. and Treimant, S.B. (1953) Cosmic Radiation Intensity-Time Variations and Their Origin. I. Neutron Intensity Variation Method and Meteorological Factors. Physical Review, 90, 934-950. http://dx.doi.org/10.1103/PhysRev.90.934
- Dorman, L.I.I. and Yanke, V.G. (1975) Development of the Theory of Meteorological Effects in Cosmic Rays. Proceedings from the 14th International Cosmic Ray Conference, Munchen, 15-29 August 1975, 1385.
- Kurguzova, A.I. and Charakhchian, T.N. (1979) Temperature Effect of the Muon Component of Cosmic Rays in the Atmosphere. Geomagnetism and Agronomy, 18, 403-407.
- Bercovitch, M. (1967) Atmospheric Effects on Cosmic Ray Monitors. Proceedings of the 10th International Cosmic Ray Conference, Calgary, 19-30 June 1967, 269.
- Wolberg, J.R. (1967) Prediction Analysis. D. Van Nostrand, Princeton.
- Rigozo, N.R., Echer, E., Nordemann, D.J.R., Vieira, L.E.A. and Faria, H.H. (2005) Comparative Study between Four Classical Spectral Analysis Methods. Applied Mathematics and Computation, 168, 411-430. http://dx.doi.org/10.1016/j.amc.2004.09.031
- Dragic, A., Banjanac, R., Udovicic, V., Jokovic, D., Puzovic, J. and Anicin, I. (2005) Variations of CR-Muon Intensity in the Declining Phase of the 23rd Solar Cycle in Ground and Shallow Underground Data. Proceedings of the 29th International Cosmic Ray Conference, Pune, 3-10 August 2005, 101-104.
- Kirkby, J., Mangini, A. and Muller, R.A. (2004) The Glacial Cycles and Cosmic Rays. European Organization for Nuclear Research, CERN-PH-EP/2004-027, 1-16.
- Da Silva, M.R., Gonzalez, W.D., Echer, E., Dal Lago, A., Vieira, L.E.A., Guarnieri, F.L., Lucas, A., Schuch, N.J. and Munakata, K. (2007) Multitaper Spectral Analysis of Cosmic Rays Sao Martinho da Serra’s Muon Telescope and Newark’s Neutron Monitor Data. Revista Brasileira de Geofísica, 25, 163-167. http://dx.doi.org/10.1590/S0102-261X2007000600019
- Dorman, L. (2004) Cosmic Rays in the Earth’s Atmosphere and Underground. Kluwer Academic Publisher, Dordrecht. http://dx.doi.org/10.1007/978-1-4020-2113-8
- Vieira, L.R., Dal Lago, A., Rigozo, N.R., Da Silva, M.R., Braga, C.R., Petry, A. and Schuch, N.J. (2012) Near 13.5- Day Periodicity in Muon Detector Data during Late 2001 and Early 2002. Advances in Space Research, 49, 1615-1622. http://dx.doi.org/10.1016/j.asr.2012.01.017


