International Journal of Geosciences
 Vol.4 No.6A2(2013), Article ID:36008,7 pages DOI:10.4236/ijg.2013.46A2001

Invariance in the Seasonal Median Dates for Mono-Modal Monsoonal Rainfall Distribution over the Semi-Arid Ecotone of Sub-Saharan West Africa

Naraine Persaud1*, Moustafa Elrashidi2, Xiaobo Zhou3, Xining Zhao4, Xiaoli Chen4

1Department of Crop and Soil Environmental Sciences, Virginia Polytechnic Institute and State University, Blacksburg, USA

2Natural Resources Conservation Service, Lincoln, USA

3Department of Agricultural and Biosystems Engineering, Iowa State University, Ames, USA

4Institute of Water Saving Agriculture in Arid Areas of China, Northwest A&F University, Yangling, China

Email: *npers@vt.edu

Copyright © 2013 Naraine Persaud et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received June 12, 2013; revised July 22, 2013; accepted August 14, 2013

Keywords: Inter-Tropical Front; Inter-Tropical Convergence Zone; Semi-Arid Rainfall Prediction; Humanitarian Food Assistance; Food Insecurity; Semi-Arid Tropics; Niger; Burkina Faso

ABSTRACT

Seasonal distribution of mono-modal, monsoonal rainfall across the semi-arid ecotone of sub-Saharan of West Africa is highly variable and unpredictable. The ever-present risk of drought and crop failure in this environment often results in food shortages that are met by emergency food aid. Humanitarian assistance planners would be better prepared for such interventions in a timely manner if they have reliable indicators that forewarn the impending failure of the rains. A good indicator would be a characteristic of the seasonal rainfall distribution that can be shown to be reasonably invariant over time and space. The objective of this study is to investigate whether such invariance existed for the seasonal median date (meaning the date when 50% of the seasonal total occurs). Such invariance is expected since the sun’s cyclic declination forces the advance and retreat of the Inter-tropical Front over West Africa. We examined the statistical properties of the seasonal median date for 1349 station-years of rainfall records for 30 rainfall stations in Burkina Faso and Niger with coordinates ranging from 9.88˚ to 18.5˚ north latitude and −4.77˚ to 13.2˚ longitude. The results showed that the median date was quite narrowly distributed over years with rather weak dependence on geographical coordinates. It can therefore be used as a reasonable ex-ante indicator of the success or failure of the rains as the rainy season progress.

1. Introduction

The climate of sub-Saharan West Africa changes from rainless and arid at latitudes on the fringe of the Sahara desert to wet and humid close to the equator. The semiarid tropical ecotone between these climatic extremes straddles portions of many West African nations from the Cap Verde Islands in the west through Chad in the east. Agro-ecologically, over 50% of sub-Saharan West Africa is semi-arid (climate Bsh according to the Koppen-GeigerPohl classification system) with annual average temperature > 20˚C [1].

In their landmark study on the point rainfall patterns over sub-Saharan West Africa, Coheme and Franquin [2] showed that the mean annual rainfall isohyets over this region were almost parallel and oriented east-west, with rainfall decreasing progressively with increasing latitude. Their findings were in accordance with those previously suggested by Chevalier [3] and Trochain [4] based on eco-botanical observations. This progressive increase in the mono-modal, monsoonal, rainfall amount and distribution with decreasing latitude south of the Sahara is the primary factor controlling the agriculture, ecology, and demography of the semi-arid ecotone of sub-Saharan West Africa [5,6].

The underlying reason for the progressive decrease in rainfall with increasing latitude is the annual northward advance and retreat of the Inter-tropical Convergence Zone (ITCZ). On satellite images, the ITCZ appears as a quasi-permanent band of clouds girdling the equator and separating the air masses of the earth’s northern and southern hemispheres. Over tropical Africa, the ITCZ regularly oscillates north and south of the equator due to the differential heating of the air masses in the northern and southern hemispheres as the earth orbits the sun [7, 8]. With advance of the ITCZ, the dry, dust-laden, cooler northeast trade winds (termed as the harmattan) interact with the south-westerly warm, monsoonal, humid air flowing from the Gulf of Guinea. Periodic instabilities (termed as easterly African wave disturbances) develop in the transition zone (sometimes called the Inter-Tropical Front or ITF) between these air masses, and give rise to unpredictable, randomly distributed, short-duration convective storms that are often preceded by dust storms [9-11]. The mono-modal annual rainfall distribution at a given location in the semi-arid zone is entirely associated with the convective instabilities that develop as long as the ITCZ persists over the particular location.

The annual northward advance and retreat of the ITCZ is a determined and stable phenomenon. However, the advance is not continuous. It is a pulsed phenomenon but the advances and pauses are irregular [12]. The onset of its advance, how fast it advances, how fast it retreats, how far northward it reaches, the frequency of occurrences of the African wave disturbances, and how much rain results, are factors that change within the rainy season and from year to year. The result is a highly variable, unreliable, and practically unpredictable, intra-annual and inter-annual point rainfall pattern accompanied by high risk of drought, dryland crop failure, and famine. Many studies have quantified these aspects of point rainfall distribution over the West African, semi-arid ecotone [13, 14].

Widespread failure of the rains in any given year results in famine, death, and devastating socio-economic impacts. The disastrous famine due to the unprecedented failure in consecutive years from 1969 through 1974 across the entire sub-Saharan semi-arid belt focused worldwide attention, socio-economic aid, and intervention in this region [15]. Since rainfall did not fully reach the pre-1969 levels [16], many countries plan for delivering emergency humanitarian food aid to mitigate possible famine in this region. If failure of the rains can be reliably predicted ex-ante, it would help planners in these agencies to better plan their relief activities and respond in a more timely manner [17,18].

The ITF passes over any given latitude between 0˚ and 23.5˚ twice during the rainy season. The first time occurs during the ITCZ advance and the second during its retreat. Similarly, at latitudes below 23.5˚ the sun is directly overhead twice during a given year. The cyclical advance and retreat of the ITCZ is in synchrony (or at least associated with) with the cyclic behavior of the sun’s declination due to earth’s annual rotation around the sun. The first passage of the sun at a given latitude would herald the start the rains and the second the end of the rains. This would imply that the median date (meaning the date when 50% of the seasonal total occurs) of the rainfall distribution in any season ought to be invariant regardless of latitude. If it turns out that the median date was exactly fixed then it would be a perfect ex-ante indicator of impending success or failure of the rains. On that fixed date there would be 100% confidence that the rainfall total received before that date would be the same total that would be received after that date.

It would be unrealistic to think that there would be a unique median date for rainfall over the entire semi-arid zone of West Africa since local episodic factors and influences are always superimposed on the embedded cycles in meteorological observations. Nevertheless, the median date could still be a useful predictor depending on the nature of its distribution over years at a given location. If the seasonal median dates over the years of record for a given station were normally distributed, then there would be a 50:50 chance that the rainfall prior to distribution’s mean value would be the same after that date. If no rainfall is recorded with each passing day after this date, humanitarian assistance and famine relief planners can be more and more confident of the risk of failure (or success) of the rains. The narrower the median date distribution the more useful it would be as an ex-ante indicator of failure or success. In this context, the following questions need to be answered about the seasonal median dates. Is it normally distributed around its mean value? Is it narrowly distributed? How narrow is the distribution? Is it narrow for all stations regardless of location (meaning latitude and longitude)? The objective of this study was to seek answers to such questions by examining the statistics of the median date of the rainy season obtained from analysis of synoptic point rainfall.

2. Material and Methods

2.1. Data

Available records of decadal rainfall totals for all synoptic stations in Burkina Faso and Niger up to the year 2000 were collected. Burkina Faso and Niger are 2 neighboring countries that entirely straddle the semi-arid zone in sub-Saharan West Africa. Taken together, the southernmost point of the border of Burkina Faso is about 9˚20' and the northernmost point of the Niger border is about 23˚30' north latitude. Likewise the western border of Burkina Faso and the eastern border of Niger fall within 5˚30' east to 16˚0' west longitude. The land area of for Niger (1.27 × 106 km2) is about 4.5 times that of Burkina Faso (0.273 × 106 km2), but the latter supports a greater population (17.3 versus 16.3 million inhabitants). This higher population carrying capacity is largely due to its more southern location in the semi-arid zone.

The rain gauge network density in these countries decreases with increasing latitude. There were 129 stations in Burkina Faso and 162 stations in Niger with 4701 station-years and 5374 station-years of records respectively. The mean annual rainfall over 46 years of record for Batie with latitude 9.88˚ was 1134 mm. The corresponding value over 44 years of record for Ingall with latitude 17.42˚ was 179 mm. The latitudinal gradient in mean annual rainfall between these stations was 127 mm per degree. Data for 30 of these stations each with 15 or more years of record were selected for further analysis and checked for quality (Figure 1). The final data set for these 30 stations had 1349 station-years of records and their coordinates ranged from 9.88 to 18.5 degree north latitude and −4.77 to 13.2 degree longitude. The data for each year consisted of an array of 36 values (in mm) of decadal rainfall totals.

2.2. Data Analysis

The rainfall data were used to extract the median date of the rainy season for each of the 1349 station-years of record. Initial data quality checking showed records for many years were duplicated or that there were duplicated lines in the data for a given year. The computer read program was designed to check for such miscoding and to delete duplications. There were some, but not many, missing station-years of records.

There is no rainfall anywhere prior to May and after October in any year. Therefore any year missing rainfall totals for one or more decades numbered 10 through 30 were removed from the data to be used for further analysis. Quality-checked data files were generated for each station consisting of 5 comma delimited columns namely: station name, year of record, decade number from 1 through 36

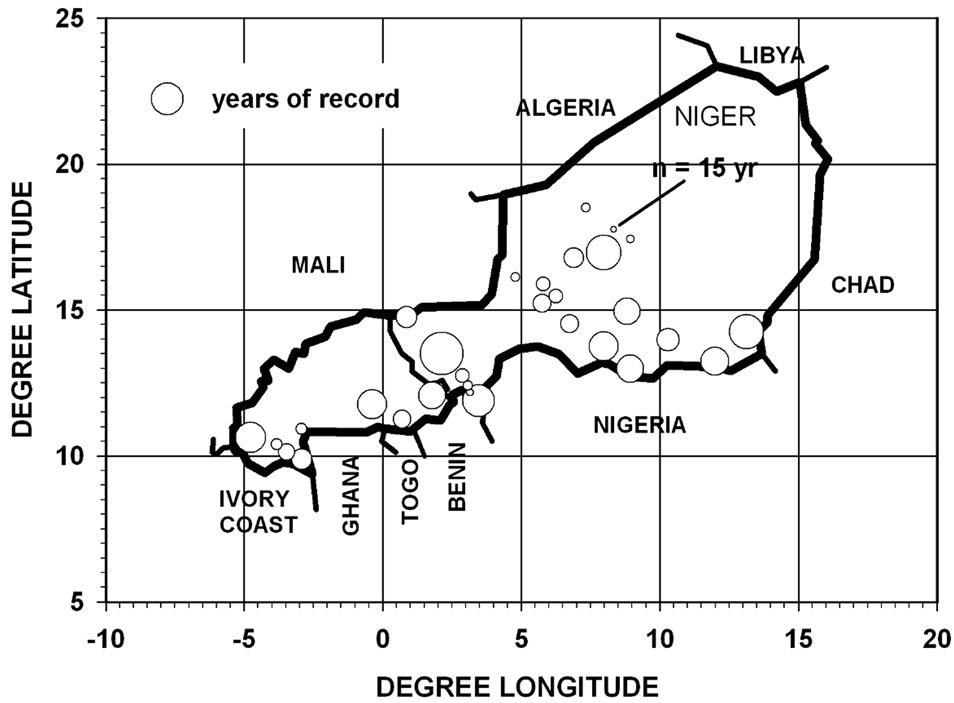
Figure 1. Map with bubble plot showing coordinates and years of records for 30 rainfall stations in Burkina Faso and Niger selected for analysis ranging from 9.88 to 18.5 degree north latitude and −4.77 to 13.2 degree longitude. Each had 15 years or more of records for a total of 1349 station-years.

(the third decade of any month was taken as 21 though the end of the month), day of year corresponding to the midpoint of the decade in question (for example day 115 would be the midpoint between 21 through 30 April or decade number 12), and the rainfall total in mm for the decade.

These quality-checked data files were used as input for calculating the seasonal median date for each year (as the day of year counting from 1 on January 1). First the cumulative fraction of the seasonal rainfall total as a function of day of the year was calculated. The day of the year corresponding to values of cumulative fraction = 0.125 and 0.875 were then calculated by linear interpolation. The interval in days between these two limits was calculated and represents the middle 75% of the seasonal rainfall for a given year. This interval was chosen because the values between these limits fell on the linear portion of the typical sigmoid-shaped seasonal cumulative rainfall distribution curve. A straight line, namely: cumulative fraction = a*day + b, was then fitted through the points between these limits. The equation was then solved to yield the day of year (i.e. the median date) when the cumulative fraction was equal to 0.5. Figure 2 graphically illustrates the working of this algorithm. The mean and standard deviation of the median dates over the years of record for a given were calculated from the results obtained for each station.

3. Results and Discussion

The first question was the form of the distribution of the median dates over years for a given station. Figure 3 is a plot of the median and mode versus the mean for the values of the rainfall median date obtained for the 30 rainfall stations in Burkina Faso and Niger. If the distribution were normal for a given station, values for the mean, median, and mode would be the same and would

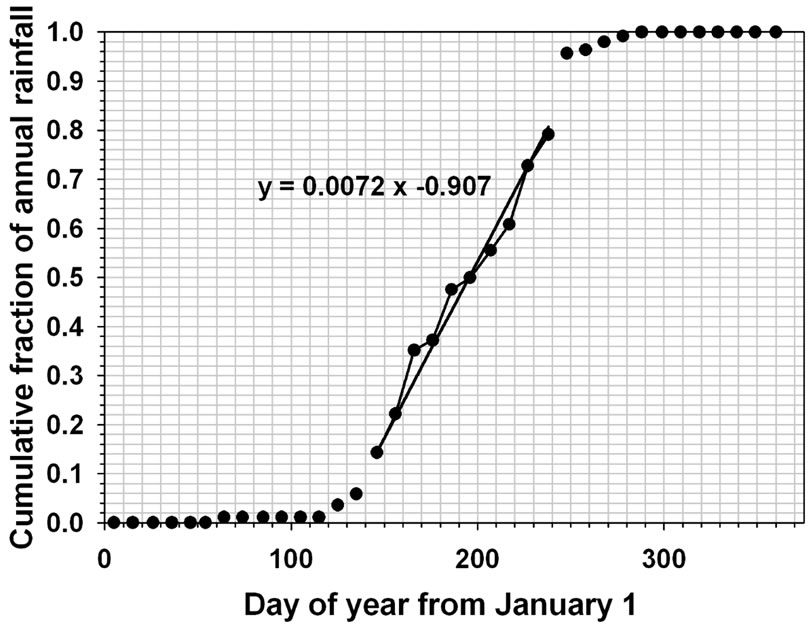
Figure 2. Illustrating the algorithm (see text for details) used to extract the median mono-modal rainfall date for a given year of rainfall records. Example for Gaya, Niger, north latitude 11.88˚, east longitude 3.45˚ for year 1932.

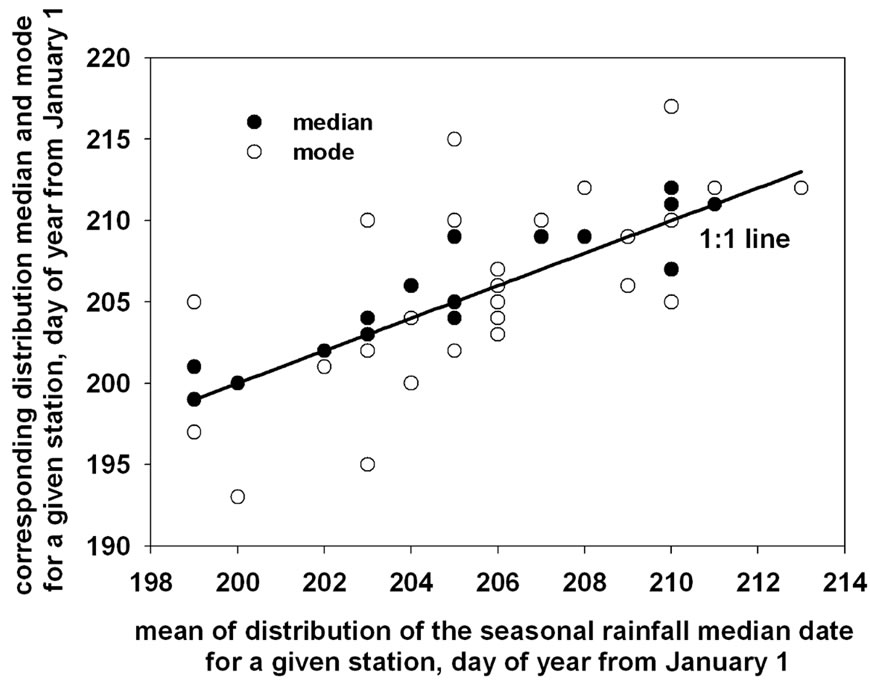
Figure 3. Plot of the median and mode versus the mean of the distribution of the values for the seasonal rainfall median dates obtained for 30 rainfall stations with a total of 1349 years of records in Burkina Faso and Niger. Stations on the 1:1 line would indicate a perfectly normal distribution.

fall on the 1:1 line in Figure 3. There were 4 stations with mean = median = mode, 15 with mean = median, and 6 with mean = mode. The mean and median differed by 1 day for 29 stations, and the mean differed from the mode by 1 day for 20 stations. These results indicate very close to normal distributions for over 95% of the stations.

The median date distribution for several of stations were examined to verify that this was the case and the example for Gaya, Niger, with coordinates 11.88˚ north latitude and east longitude 3.45˚ is shown in Figure 4. This station had 69 years of record and the range of values for the median date was 185 to 223 with standard error of the mean = 0.91.

The frequency of finding the median date in 5-day intervals starting at 180 day were tallied and the probabilities calculated by dividing the frequency by the number of year of records. The data points in Figure 4 represent these probabilities. The theoretical line was calculated using the mean value (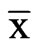) of 205 day and the standard deviation (s) = 7 day obtained for the sample of 69 median dates in the equation for the normal probability density distribution namely,

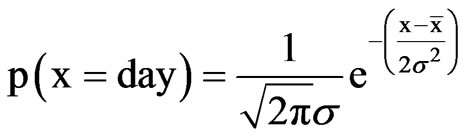(1)

with the range of x from 185 to 225 day.

As shown, the distribution for this example was quite narrow and it could be said that in about 70% of the years the median date of the rainy season would occur between 198 and 212 day after January 1 (i.e. between 16 and 30 July). Therefore, after July 16 humanitarian and famine relief and assistance planners can be more and more confident that, if there is no rainfall with each passing day, the risk increases that the total rain received prior to July 16

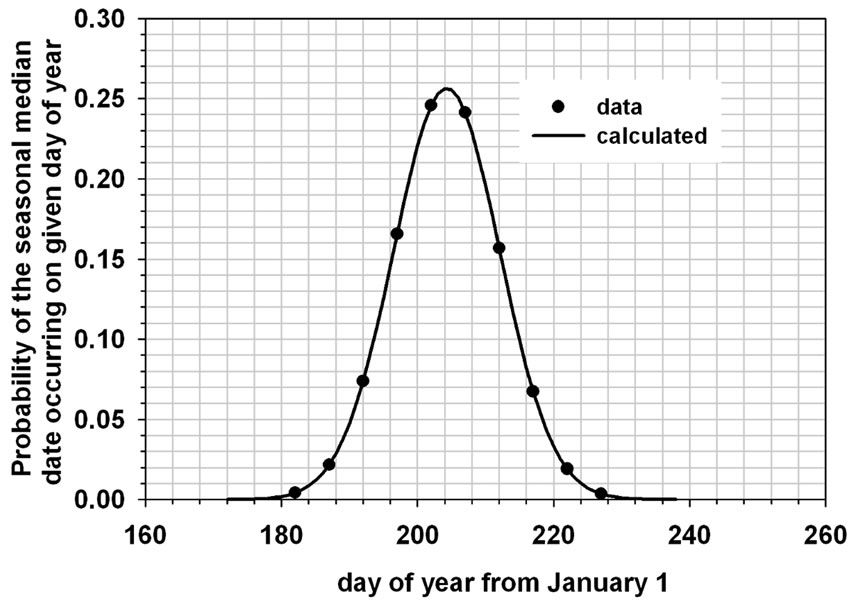
Figure 4. Typical result obtained for the distribution of the median dates. Example for station Gaya, Niger, north latitude 11.88˚, east longitude 3.45˚ with 69 years of rainfall record.

would be the predicted rainfall for the rest of the season. There is a 50:50 chance that the rainfall prior to day 205 (i.e. July 23 corresponding to the mean value) would be the same after July 23. The algorithm exemplified in Figure 2 can easily be adapted to obtain the distribution of dates for any percentage other than 50% (i.e. the midpoint of the rainy season). Thus the straight line fitted for the example in Figure 2 can be used to estimate the date for 75% of the rainfall. Denoting this as day0.75, its distribution for any given station can be generated and used as an ex-ante indicator in the same manner as day0.50.

Humanitarian assistance planners can use such results to generate a sequential series of GIS-based maps showing for each recording station, 1) the current season’s total up to a given date, and 2) an estimate of the increasing risk of failure (or success) based on the analysis of the historical seasonal median date distribution. Such maps generated periodically for all stations can be used to pinpoint likely areas of vulnerability as the rainy season progresses for the entire semi-arid region of sub-Saharan West Africa. Further assessment of the potential usefulness of this near real-time application of measured point rainfall would require similar analyses for all stations in this region.

In this context, the important question is: are the characteristics of the median date distribution the same for all stations regardless of location (meaning latitude and longitude) or do they change and how? Figure 5 is a polar plot showing results of the mean values of the median date for all 30 stations as a function of latitude and longitude coordinates. The circular scale of the polar plot is in degree from −5 to 18.75 in steps of 1.25. The scale of the spokes is the day of the year from January 1 corresponding to the mean of the median date distribution for each station and ranges from 190 day (center of the polar plot) to 220 day. It is clear that regardless of latitude or longitude, the mean of the median date distribution for 26 of the 30 stations fell between 200 and 210 day (corresponding

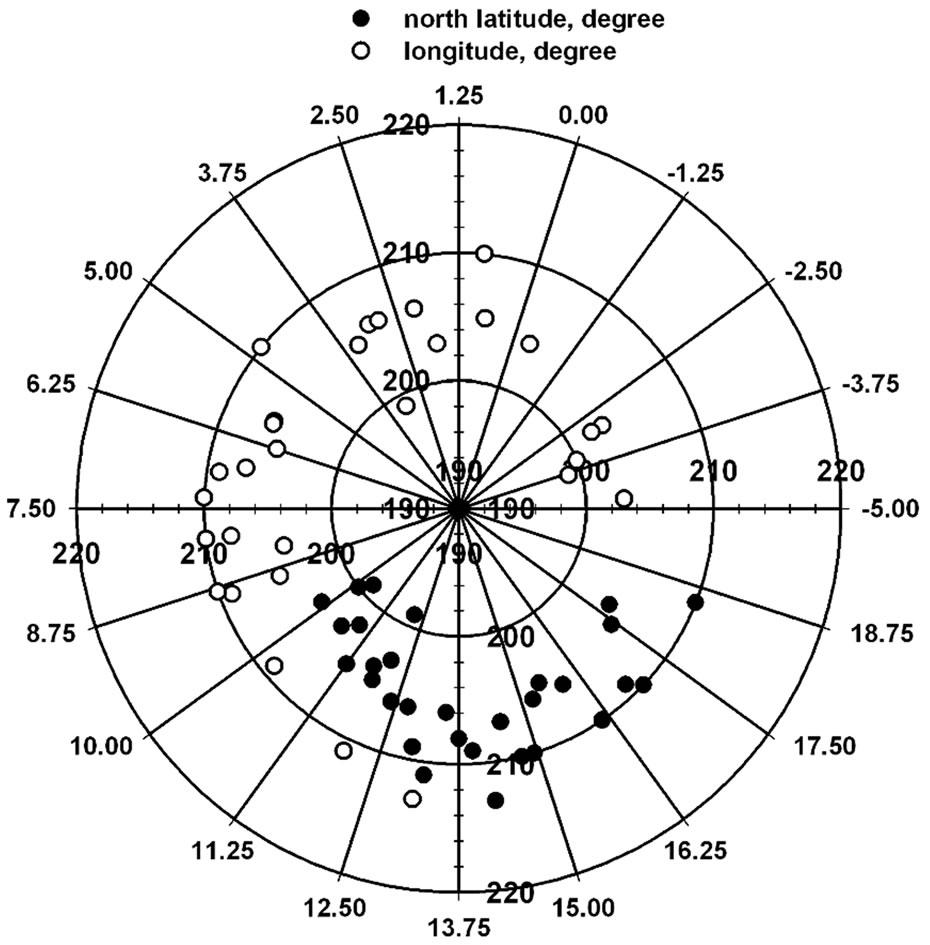
Figure 5. Polar plot showing dependence of the mean of the median date distribution on latitude (from 9.88 to 18.5 degree north) and longitude (from −4.77 to 13.2 degree) for 30 rainfall stations in Burkina Faso and Niger.

to 18 July through 28 July). Overall mean for all stations (n = 30) was 206 day with standard deviation = 3.6 day within a range = 199 to 213 day. As would be expected from the Central Limit Theorem, the 30 values of the mean were normally distributed with median and mode = 206 day.

Close examination of Figure 5 shows that there is also some, albeit very weak, dependence of the median date on both latitude and longitude. Figure 6 is a multivariate bubble plot of the mean of median date distribution on both latitude and longitude to further explore the dependence. To accentuate differences bubbles for each station were scaled to represent the distribution mean value minus 190 day. The clustering in Figure 6 is very weak.

As shown in Figures 5 and 6 the median date was reasonably invariant over years and over a wide range of latitude and longitude. Such invariance is expected since sun’s cyclic declination forces the advance and retreat of the Inter-tropical Front over West Africa. Figure 7 illustrates how the annual periodicity of sun’s declination in the northern hemisphere as a function of day after January 1 would theoretically mirror the oscillation of the ITCZ over West Africa.

The declination (d) was calculated using the astronomical formula as d in radian = 0.006918 – 0.399912 cosj + 0.07257 sinj – 0.006758 cos2j + 0.000907 sin2j – 0.002697 cos3j + 0.00148 sin3j where j is the day angle in radian given as j = 2p(J – 1)/365 where J is the day number counted from 1 on January 1 to 365 on December 31 [19]. The values were multiplied by 180/p to

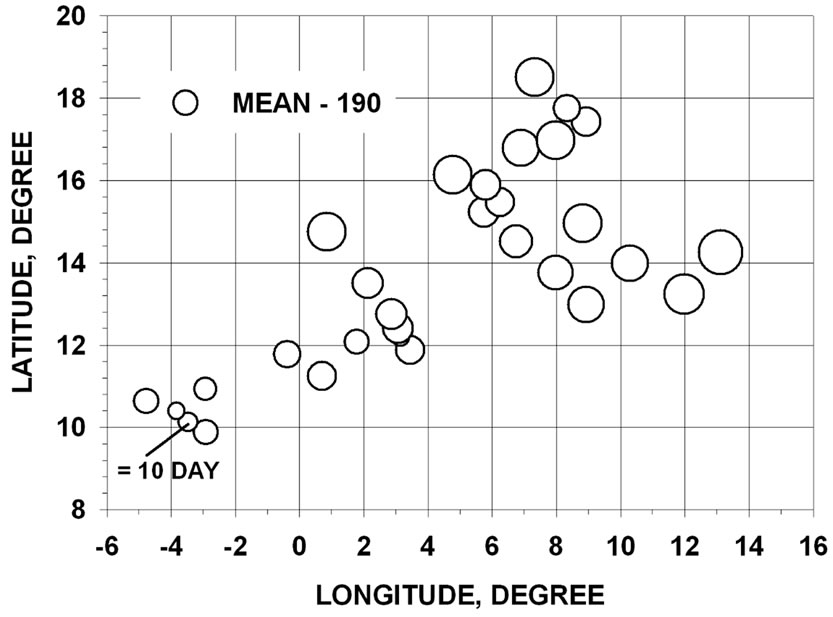
Figure 6. Multivariate bubble plot showing the mean of the median date distribution versus longitude and latitude for 30 rainfall stations in Burkina Faso and Niger. To better highlight differences between stations, bubbles were scaled to represent the mean value minus 190 day.

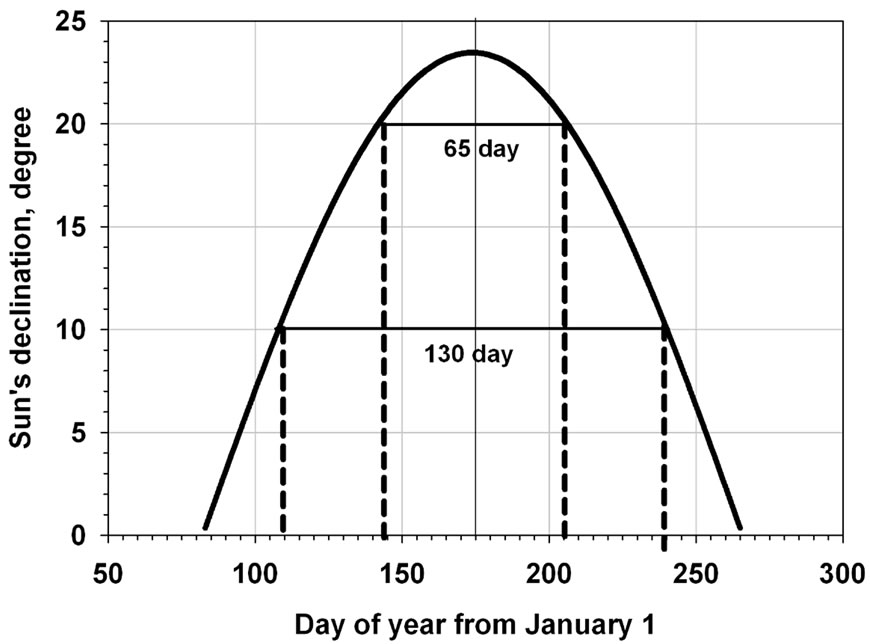
Figure 7. Sun’s declination (degree) in the northern hemisphere as a function of day after January 1.

convert to degrees.

As shown, the sun would be directly overhead at noon twice for any given latitude below 23.5˚. If these occurrences herald the start and end of the rainy season for a given latitude, then the duration of the season would vary but the midpoint (i.e. the median date of the point rainfall record) would be expected to be invariant.

Thus the duration at 10 degree north latitude would be 110 to 240 = 130 day, at 15 degree north latitude 123 to 225 = 102 day, and at 20 degree north latitude 145 to 205 = 60 day (Figure 7). The estimated rainy season duration is a non-linear decreasing function of latitude. Thus the decrease from 10˚ to 15˚ north latitude is 28 day whereas for the same interval from 15˚ to 20˚ the decrease is 42 day.

The duration of the middle 75% of the rainy season total for station Gaya in Niger with latitude close to 12˚ can be estimated from the mean value of the days elapsed between cumulative fractions 0.125 and 0.875 (exemplified in Figure 2 and here denoted as d0.875 - d0.125). This mean value of d0.875 - d0.125 over 69 years was 97 ± 14 day standard deviation and (not expectedly) less than the duration from Figure 7 of 117 day (i.e. from day 115 to 132). The actual duration of the rainy season would be rather hard to define because there can be many choices of the rain-event used to define its start and end. The value d0.875 - d0.125 representing middle 75% of the rainy season is more rigorously defined.

It is clear that increasing this middle percentage (for example d0.95 - d0.05 or 90%) would move the rainy season duration closer to the predicted values from Figure 7. Corresponding values for d0.875 - d0.125 over 47 years for station Ayourou in Niger at latitude close to 15˚ was 68 ± 17 day compared to the value of 102 day from Figure 7. For Agadez at north latitude close to 17˚ the value of d0.875 - d0.125 was 55 ± 23 day compared to the Figure 7 value of 87 day.

The invariant mid-point in Figure 7 would be the summer solstice or about 173 days counting from January 1. The mean value of the median dates over all 1349 years of records was 206 ± 4 day. This represents a shift of about 1 month after the summer solstice. All 30 stations examined showed this shift away from summer solstice.

As examples, for Batie in Burkina Faso at north latitude 9.88˚ degree North Latitude and longitude −2.92˚, the mean (n = 46 year) of the distribution of median dates was 203 day and the shift was therefore 28 day. For Tanout in Niger at 14.95˚ degree north latitude and longitude 8.82˚ in Niger, the mean (n = 59 year) was 210 day giving a shift of 35 day. The reason for the shifts is most likely that the latitudinal location of the leading northern edge of the ITCZ (termed as the Inter-tropical Front or ITF) does not exactly coincide with the passage of the sun and may be dependent on longitude. Quantifying the dependence of these median date shifts on longitude would require an expanded analysis of the entire network of rainfall stations in West Africa.

4. Conclusion

An analysis of 1349 years of decadal rainfall records for 30 rainfall stations in Burkina Faso and Niger (with coordinates ranging from 9.88 to 18.5 degree north latitude and −4.77 to 13.2 degree longitude) showed that the seasonal median dates of the point rainfall observations were quite normally and narrowly distributed with no dependence on geographical coordinates. This statistical invariance implied that the mean of the median dates for a given station can be used as a reasonably reliable ex-ante indicator of the failure or success of the monsoon as the rainy season progresses.

5. Acknowledgements

Co-authors Dr. Xining Zhao and Dr. Xiaoli Chen would like to thank the 111 Project from the Ministry of Education and the State Administration of Foreign Experts Affairs (B12007) for supporting and facilitating their participation in this study.

REFERENCES

  1. D. Nir, “The Semi-Arid World: Man on the Fringe of the Desert,” Longman, London, 1974.
  2. J. Cocheme and P. Franquin, “An Agroclimatological Survey of a Semi-Arid Area in Africa South of the Sahara,” World Meteorological Organization Technical Note Number 86, W.M.O., Geneva, 1967.
  3. A. Chevalier, “Le Territoire Geobotanique de L’Afrique Tropicale Nord-Occidentale et ses Divisions,” Bulletin Societe Botaniques, Vol. 80, 1933, pp. 4-26.
  4. J. L. Trochain, “Les Territories Phytogeogrphiques de L’Afique Noire Francaise d’Apres leur Pluviometrie,” Revue des Travaux du Laboratoire de la Faculte de Science Montpellier, Serie Botanique, Vol. 5, 1952, pp. 113- 124.
  5. World Resources Institute, “A Guide to World Resources 2000-2001: People and Ecosystems, the Fraying Web of Life,” World Resources Institute, Washington DC, 2000.
  6. J. J. Feddema and S. Freire, “Soil Degradation, Global Warming and Climate Impacts,” Climate Research, Vol. 17, No. 2, 2001, pp. 209-216. doi:10.3354/cr017209
  7. T. Lebel, J. D. Taupin and N. D’Amato, “Rainfall Monitoring during HAPEX-Sahel. 1. General Rainfall Conditions and Climatology,” Journal of Hydrology, Vol. 188- 189, 1997, pp. 74-96. doi:10.1016/S0022-1694(96)03155-1
  8. J. N. Rayner, “Dynamic Climatology,” Blackwell Publishers Ltd., Oxford, 2001.
  9. L. M. Druyan and T. Hall, “Studies of African Wave Disturbances with the GISS GCM,” Journal of Climate, Vol. 7, 1994, pp. 1316-1323. doi:10.1175/1520-0442(1994)007<1316:TIOSFA>2.0.CO;2
  10. L. M. Druyan and T. Hall, “The Sensitivity of African Wave Disturbances to Remote Forcing,” Journal of Applied Meteorology, Vol. 35, 1996, pp. 1100-1110. doi:10.1175/1520-0450(1996)035<1100:TSOAWD>2.0.CO;2
  11. L. M. Druyan, M. Fulakeza and W. Thiaw, “Regional Model Simulations of African Wave Disturbances,” Journal of Geophysical Research, Vol. 105, No. D6, 1999, pp. 7231-7255. doi:10.1029/2000JD900017
  12. S. Janicot and B. Sultan, “Intraseasonal Modulation of the Convection in the West African Monsoon,” Geophysical Research Letters, Vol. 28, No. 3, 2001, pp. 523-526. doi:10.1029/2000GL012424
  13. O. Ojo, “The Climate of West Africa,” Heineman, London, 1977.
  14. J. B. Omotosho, “Long-Range Prediction of the Onset and End of the Rainy Season in the West African Sahel,” International Journal of Climatology, Vol. 12, No. 4, 1992, pp. 369-382. doi:10.1002/joc.3370120405
  15. United States Congress, “Drought and Famine in West Africa: Hearing before Ninety-Third Congress, Committee on Foreign Relations, Sub-Committee on African Affairs,” US Government Printing Office, Washington DC, 1973.
  16. S. E. Nicholson, B. Some and B. Kone, “An Analysis of Recent Rainfall Conditions in West Africa, Including the Rainy Seasons of the 1997 El Niño and the 1998 La Niña Years,” Journal of Climate, Vol. 13, No. 14, 2000, pp. 2628-2640. doi:10.1175/1520-0442(2000)013<2628:AAORRC>2.0.CO;2
  17. A. L. Chappel and C. T. Agnew, “Modeling Climate Change in West African Sahel Rainfall (1931-90) as an Artifact of Changing Station Locations,” International Journal of Climatology, Vol. 24, No. 5, 2004, pp. 547- 554. doi:10.1002/joc.1021
  18. C. Brahic, “Waiting for the Mosoon,” Science, Vol. 313, No. 5787, 2006, pp. 608-609. doi:10.1126/science.313.5787.608
  19. P. Duffett-Smith, “Astronomy with Your Personal Computer,” Cambridge University Press, Cambridge, 1990. doi:10.1017/CBO9780511564888

NOTES

*Corresponding author.

Journal Menu >>