Journal of Flow Control, Measurement & Visualization
Vol.07 No.03(2019), Article ID:93682,19 pages
10.4236/jfcmv.2019.73011
Flow-Induced Stream-Wise Vibration of Circular Cylinders
Atsushi Okajima, Takahiro Kiwata
Kanazawa University, Kakuma-machi, Kanazawa, Ishikawa, Japan
Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 1, 2019; Accepted: April 5, 2019; Published: July 15, 2019
ABSTRACT
Results from a series of studies on the stream-wise vibration of a circular cylinder verifying Japan Society of Mechanical Engineers Standard S012-1998, Guideline for Evaluation of Flow-induced Vibration of a Cylindrical Structure in a Pipe, are summarized and discussed in this paper. Experiments were carried out in a water tunnel and in a wind tunnel using a two-dimensional cylinder model elastically supported at both ends of the cylinder and a cantilevered cylinder model with a finite span length that was elastically supported at one end. These cylinder models were allowed to vibrate with one degree of freedom in the stream-wise direction. In addition, we adopted a cantilevered cylinder model that vibrated with two degrees of freedom in both the stream-wise and cross-flow directions under the same vibration conditions as an actual thermocouple well. The value of the Scruton number (structural damping parameter) was changed over a wide range, so as to evaluate the value of the critical Scruton number that suppressed vibration of the cylinder. For the two-dimensional cylinder, two different types of stream-wise excitations appeared in the reduced velocity range of approximately half of the resonance-reduced velocity. For the stream-wise vibration in the first excitation region, due to a symmetric vortex flow, the response amplitudes were sensitive to the Scruton number, while the shedding frequency of alternating vortex flow was locked-in to half of the Strouhal number of vibrating frequency of a cylinder in the second excitation region. In addition, the effects of the aspect ratio of a cantilevered cylinder on the flow-induced vibration characteristics were clarified and compared with the results of a two-dimensional cylinder. When a cantilevered circular cylinder with a finite length vibrates with one degree of freedom in the stream-wise direction, it is found that acylinder with a small aspect ratio has a single excitation region, whereas a cylinder with a large aspect ratio has two excitation regions. Furthermore, the vibration mechanism of a symmetric vortex flow was investigated by installing a splitter plate in the wake to prevent shedding of alternating vortices. The vibration amplitude of acylinder with a splitter plate increased surprisingly more than the amplitude of a cylinder without a splitter plate. For a cantilevered cylinder vibrating with two degrees of freedom, the Lissajous figure of vibration of the first excitation region shows the trajectories of elongated elliptical shapes, and in the second excitation region, the Lissajous trajectories draw a figure “8”. The results and information from these experimental studies proved that Standard S012-1998 provides sufficient design methods for suppressing hazardous vibrations of cylinders in liquid flows.
Keywords:
Flow-Induced Vibration, Flow Visualization, Bluff Body, Circular Cylinder, Scruton Number, Finite Spanlength, Aspect Ratio, Stream-Wise Vibration, Cross-Flow Vibration, One and Two Degrees of Freedom

1. Introduction
Bluff bodies are structures having non-streamlined cross-sections, such as circular, square, and rectangular cylinders, around which flows separate from the body surface. The shear layers on surfaces of a bluff body build up, causing flow separation from the body, so as to form a region of reversed flow behind the body. Subsequently, vortex flows are periodically shed into the wake. The static fluid-dynamic characteristics of a stationary bluff body change greatly depending on the behavior of the shear flow and the wake [1] . Furthermore, the flow-induced vibration of a bluff body occurs in both the cross-flow and stream-wise directions under certain conditions. Research on the flow-induced vibration of a bluff body has been of great interest for many decades because these phenomena frequently occur in industrial structures, such as those in nuclear power plants, thermal power plants, and petroleum/chemical plants, and in offshore structures and chimneys. Therefore, numerous studies have examined the flow-induced vibration of a bluff body, as reviewed in depth by Sarpkaya [2] [3] , Bearman [4] , and Naudascher [5] . Most researchers, such as Bishop and Hassan [6] and Scruton [7] focused on the cross-flow vibration of a circular cylinder with large amplitudes caused by the so-called vortex excitation near the resonance velocity. However, relatively few studies have looked at the stream-wise vibration occurring in the region of low velocity that is about half of the resonance velocity. Around 1968, an accident involving the stream-wise vibration of marine structures at low reduced velocities in a tidal current in England was reported by Wooton et al. [8] . Subsequently, King et al. [9] carried out experiments on the stream-wise vibration of a flexible cantilevered circular cylinder with a long aspect ratio of 41 in an open water channel to investigate the causes of this accident. As a result, it was found that when the value of the Scruton number (the reduced structural mass-damping parameter) Cn is very small, two excitation regions of stream-wise vibration appear at reduced velocities close xito half of the resonance velocity; that is, the first excitation region that accompanies the symmetric vortex flow exists at low velocity and the second region due to the alternating vortex flow appears at a relatively high velocity. In 1995, accidental sodium leakage at the Monju prototype fast breeder reactor in Japan occurred because a thermocouple well in the secondary coolant piping system failed due to flow-induced vibration [10] . The failure was caused by the high-cycle fatigue resulting from the flow-induced stream-wise vibration of the thermocouple well. As a countermeasure against such accidents, the Japan Society of Mechanical Engineers (JSME) published Standard S012-1998, Guideline for Evaluation of Flow-induced Vibration of a Cylindrical Structure in a Pipe [11] [12] . Then, several experimental studies investigating the cause of this accident were conducted in water tunnels, because the density of molten sodium flowing at 480˚C in the secondary coolant piping system was close to the density of water.
When we scrutinized the results of the wind tunnel experiments by Scruton [7] on the cross-flow vibration of a circular cylinder, we found that the response characteristics of an elastically cantilevered cylinder with a finite span length are quite different from those of a two-dimensional circular cylinder elastically supported at both ends (hereafter, referred to as a two-dimensional cylinder) [13] [14] . Thus, it is important to acquire the response characteristics of the stream-wise vibration of a cantilevered cylinder with a finite span length to evaluate the critical values of the Scruton number Cn that sufficiently suppresses vibration. Then, experiments were carried out using the cantilevered cylinder models with a finite span length having aspect ratios of 5 to 21 and elastically supported at one end [15] [16] . The values of the Scruton number Cn of cantilevered cylinders were changed over a wide range to evaluate the critical value of Cn at which the stream-wise vibration of a cylinder with one degree of freedom was suppressed. Thus, the influence of the aspect ratio of cantilevered cylinders on the flow-induced vibration characteristics was clarified and compared with the results for a two-dimensional cylinder. In addition, experiments were conducted on vibrating models having two degrees of freedom in both the stream-wise and cross-flow directions in water tunnels under the same vibration conditions as actual thermocouple wells in a piping system. The effects of the turbulence of flows and the taper-ratio of a circular cylinder on the stream-wise vibration also were examined [17] [18] .
In this paper, we summarize and discuss the experimental results of circular cylinders of various shapes under different vibration conditions.
2. Experimental Arrangements
2.1. Water Tunnel
The water tunnel shown in Figure 1, which had a rectangular test section measuring 400 mm × 167 mm, was used in the experiments. The uniform flow velocity U ranged from 0.2 m/s to 1.8 m/s under a turbulence intensity of less than
Figure 1. Water tunnel apparatus [15] .
0.02. Reynolds number Re = Ud/ν, where ν is the kinematic viscosity of water, was in the range of 8 × 103 to 4 × 104.
The two-dimensional circular cylinder model had a diameter d = 20 mm and effective span length Le = 163 mm. Two circular end plates 80 mm in diameter (about 4d) and 0.5 mm in thickness were attached to both ends of the cylinder. Figure 2 shows the details of the experimental setup. Because the two-dimensional cylinder model was elastically supported at both ends by four leaf springs, it could vibrate only in the stream-wise direction. The Scruton number Cn was defined as 2mδLe/ρd2 (m is a mass unit span length of a cylinder in water), where δ is the logarithmic structural damping value of a cylinder vibrating in water. The response amplitude x of the cylinder vibrating in the stream-wise direction was detected by a laser displacement sensor, and the non-dimensional response amplitude ξ was defined as x/d. The fluctuating water velocity was detected by employing a hot-film probe located along the outer edge of the wake. In this way, we acquired the predominant values of the Strouhal number Stw = fwd/U in the wake (where fw is the fluctuating frequency of the wake flow).
2.3. Cantilevered Circular Cylinder Model with Finite Span Length for Vibration with One Degree of Freedom in Stream-Wise Direction
Figure 3 shows the experimental set-up of a cantilevered circular cylinder where the aspect ratio AR (=Le/d, where Le is span length) was varied from 5 to 21. The cylinder model was elastically supported by a leaf spring and rubber sheet attached to the ceiling of the test section. The natural frequency fc of the cylinder in water was adjusted to be a constant value between 20 Hz to 30 Hz by using different leaf springs. The reduced velocity Vr (=U/fcd) was varied from 0.9 to 4.0 by changing the water velocity. The logarithmic decrement of the structural
Figure 2. Measurement model of a two-dimensional circular cylinder for free stream-wise vibration test [15] .
Figure 3. Measurement model of a cantilevered circular cylinder for free stream-wise vibration test [15] .
damping value of the vibrating cylinder model δ was varied by clamping aluminum plates and rubber plates with leaf-springs. The fluctuating displacement of the vibrating cylinder model was measured by an acceleration sensor mounted to the top of the model.
2.4. Cantilevered Cylinder Model with a Finite Span Length for Vibration with Two Degrees of Freedom in Both Directions
Figure 4 shows the experimental apparatus for a cantilevered cylinder with a finite span length. The model was configured to vibrate with two degrees of freedom, that is, in both the stream-wise and cross-flow directions, which closely resembles an actual thermocouple well. The cantilevered cylinder model was
Figure 4. Experimental apparatus for a circular cylinder model elastically supported to vibrate with two degrees of freedom [17] .
elastically supported by a total of four support springs at the base, that is, two springs in the stream-wise direction and two springs in the cross-flow direction. This arrangement allowed the model to vibrate in a rigid-body mode with two degrees of freedom. The structural damping value δ was easily changed by varying the distance between the upper and lower permanent magnets sandwiching a copper plate, and then the value of the Scruton number Cn was varied according to the structural damping value δ.
3. Response Characteristics of Two-Dimensional Circular Cylinder
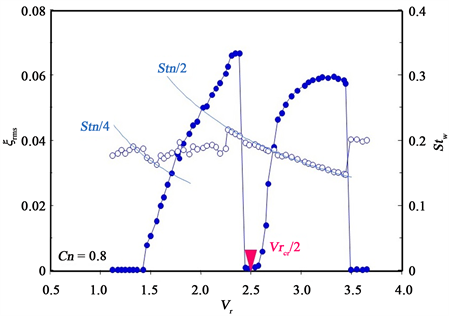
Figure 5 shows the results for the response characteristics of the two-dimensional cylinder as it vibrated in the stream-wise direction in a wind tunnel. The figure shows the root mean square (RMS) values of response amplitudes ξms of the cylinder in the stream-wise direction and the predominant values of Strouhal number Stw of fluctuating velocity in the wake, with respect to the reduced flow velocity Vr for a Scruton number of Cn = 0.80. From this figure, the vibration of the cylinder occurs around Vr = 1.4 and the amplitude ξms linearly increases with respect to Vr, reaching ξrms = 0.068. In contrast, the lock-in phenomenon, where the frequency of a wake fw equals fc/4 of the natural frequency fc for a vibrating cylinder, appears only in a narrow range around Vr = 1.5. This lock-in phenomenon is not observed in the wide range of Vr = 1.6 to 2.25 in the first excitation region. The Strouhal number of the wake Stw is almost constant and equals the Strouhal number for a stationary cylinder Stn of 0.18 to 0.19. Thus, the excitation
Figure 5. Amplitude of a two-dimensional circular cylinder for Scruton number Cn = 0.80 [13] .
vibration of the cylinder was abruptly suppressed around Vr = 2.5, which is half of the reduced resonance velocity Vrcr = U/fnd = 1/Stn. The second excitation region appears in the high reduced-velocity region of Vr = 2.6 to 3.6, and the Strouhal number of fluctuating velocity in the wake Stw is locked to half of the Strouhal number of vibrating frequency of the cylinder (1/2Stc) in the range of Vr = 2.25 to 3.5. It is noted that this lock-in range includes the range near Vr = 2.25, where the damping force suppresses the vibration.
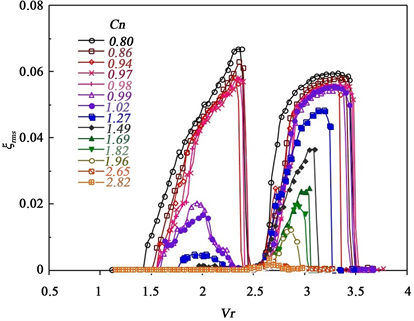
Next, Figure 6 shows the response amplitude ξrms of the cylinder in the stream-wise direction against the reduced velocity Vr, when the Scruton number Cn was varied over the range 0.80 to 2.82 by employing an electromagnetic damper. At all values for Cn, the first and second excitation regions are present in the regions of 1.4 < Vr < 2.4 at less than Vrcr/2 and the region of 2.6 < Vr < 3.5 at greater than Vrcr/2, respectively. As the value of Cn increases, the amplitudes ξrms of the two excitation regions decrease, exhibiting different response characteristics with respect to Cn; that is, in the first excitation region, the maximum value of ξrms abruptly decreases according to the increase of the value of Cn, while the value of ξrms gradually decreases in the second excitation region, and the value of the on-set velocity of excitation increases. The behavior of the flow-induced vibration characteristics was clearly different with respect to Cn in the two excitation regions. Figure 7 shows the flow patterns visualized by a smoke-wire technique [13] . In this image, the symmetric vortex pattern is observed to form at Vr = 2.3 in the first excitation region below Vrcr/2, as shown in Figure 7(a), and the alternating vortex flow pattern is found to appear at Vr = 3.2 in the second excitation region, as shown in Figure 7(b). In this way, the difference between the flow-induced vibration characteristics of the two excitation regions obviously corresponds to very different vortex patterns around a cylinder observed in the two excitation regions. These results are in good agreement with the experiments of King et al. [9] .
Figure 6. Response amplitude of a two-dimensional circular cylinder for different Scruton numbers Cn = 0.80 - 2.82 [12] .


Figure 7. Visualization of two different flow patterns around a two-dimensional circular cylinder vibrating in a wind tunnel [13] . (a) Symmetric vortex pattern in the first excitation region (Vr = 2.3); (b) Alternating vortex pattern in the second excitation region (Vr = 3.2).
In prior experiments, Aguirre [19] inserted a splitter plate behind a cylinder in a water channel and found that the vibration of the first excitation region consisted of self-excited vibration caused by the symmetric vortex flow. Thus, we inserted a splitter plate behind a cylinder to try to prevent the vortex street from shedding alternately in the wake. The length of the splitter plate was approximately l = 15d, which was longer than the plate used in Aguirre’s experiment, and the clearance between the cylinder and plate was very small, approximately 0.15d. Figure 8 shows the effect of the splitter plate on the response amplitude

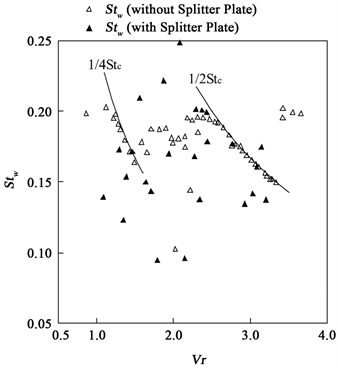
Figure 8. (a) Response amplitude ξrms and (b) wake Strouhal number Stw for two-dimensional circular cylinders for Cn = 0.70 with and without a splitter plate [15] . (a) Response amplitudes ξrms; (b) Wake Strouhal numbers Stw.
ξrms of the two-dimensional cylinder against the reduced velocity Vr, and compares it with the results for the cylinder without a splitter plate when the Scruton number Cn = 0.70. It was found that when a splitter plate was inserted, the excitation region extended from Vr = 2.0 up to 2.5, having a maximum amplitude of ξms = 0.05 at Vr = 2.5. It is noteworthy that the response amplitudes ξrms of the cylinder both with and without a splitter plate were almost equal in the range of Vr = 1.1 to 2.2, where the symmetric vortices appeared. However, behind the cylinder without a splitter plate, alternating vortex flow formed and worked to suppress vibration in the range of Vr = 2.2 to 2.8. Additionally, the response characteristics of the lock-in region at Stw = 1/4Stc and l/2Stc for the vibrating cylinder with a splitter plate are different from those of the cylinder without a splitter plate, as shown in Figure 8(b). According to Naudasher [5] , the exciting vibration in the first region is associated with the symmetric vortices formed in the near-wake region. Furthermore, it was suggested that the vibration of a cylinder without a splitter plate disappears around Vr = 2.5 by the interaction with the alternating vortices. That is, the vibration is considered to be suppressed by the alternating vortices, which generate a damping force in the limited range of Vr = 2.0 to 2.8.
Figure 9 summarizes the maximum response amplitudes ξmax of the vibrating two-dimensional circular cylinder against Scruton number Cn from the data obtained in a wind tunnel and a water tunnel [13] [14] . It is observed that two excitation regions have inherent response characteristics against the Cn values; that is, the maximum of the ξrms values drops sharply in the first excitation region as the Cn values increase. Meanwhile, the decreasing rate of ξmax against Cn value is relatively gentle in the second excitation region, and the value of ξmax becomes as small as 0.005 at a Cn value of 2.5. At this point, the vibration is considered to be suppressed. Thus, we conclude from Figure 9 that stream-wise
Figure 9. Maximum amplitude ξmax of stream-wise vibration of a two-dimensional circular cylinder against Scruton numbers Cn [15] .
vibration of a circular cylinder is suppressed under the defined conditions of Cn > 2.5 and Vr < 3.3. These results provide important data verifying JSME Standard S012-1998.
4. Response Characteristics of Cantilevered Cylinder Vibrating with One Degree of Freedom in the Stream-Wise Direction
As shown in the visualization result of Figure 10 (Re = 300 and aspect ratio AR = 10 [13] ), the flow around a stationary cantilevered cylinder with a finite span length is observed to be very different from the flow around a two-dimensional cylinder. This figure shows the flow forming a veil over the cylinder tip and thus dividing itself into tip-associated and symmetric vortex flows at the cylinder top and into alternating vortex shedding from the rest of the cylinder. Then, experiments were conducted on a cantilevered cylinder vibrating with one degree of freedom in the stream-wise direction (Figure 3). Figure 11 shows the response
Figure 10. Flow pattern around a cantilevered cylinder with tip-associated flow.
Figure 11. Response characteristics of cantilevered circular cylinders with different
characteristics of the cantilevered cylinders for which the aspect ratio AR was changed as AR = 5, 10, 14, and 21 and Cn was varied as Cn = 0.24 to 0.37 [15] , [16] . These results are compared with the characteristics of the two-dimensional cylinder with Cn = 0.70 in Figure 8 [14] . From Figure 11, it can be seen that the flow-induced vibration characteristics in the range of Vr = 1.2 to 2.0 of the first excitation region show exactly the same curve for all AR ratios. However, in the case of a small AR ratio of 5, the amplitude becomes very large near ξrms = 0.113 at the high velocity of Vr = 2.3, and then the amplitude gradually decreases between Vr = 2.5 and 3.2, resulting in a wide first excitation region accompanied by the symmetric vortex flow. When AR is smaller than 10, the second excitation region decays and vanishes due to the alternating vortex street, and only the first excitation region remains. However, when AR = 14 to 21, the vibration amplitudes are suppressed so as to form a valley at Vr = 2.4, and the amplitude increases again to the maximum value ξmax = 0.082 in the vicinity of Vr = 2.7. Then, the second excitation region exists in the range of Vr = 2.5 to 3.2, and it has the same alternating vortex flow as the two-dimensional cylinder. It is clear that the characteristics of a cylinder with a finite span length greatly depend on the aspect ratio AR.
To clarify the excitation mechanism of stream-wise vibration, a splitter plate was inserted in a wake of a cantilevered cylinder with AR = 10 to observe its effect on vortex shedding. Figure 12 compares the response results for cylinders with and without a splitter plate for Cn = 0.25. The response characteristics of a cylinder with a splitter plate have only one excitation region from Vr = 1.1 to 3.0, which consists of an increased amplitude curve from Vr = 1.1 to 2.8. It has a
Figure 12. Effects of splitter plate for the response characteristics of cantilevered circular cylinders with an aspect ratio of 10 and Cn = 0.24 [15] .
maximum value of ξmax = 0.12 at Vr = 2.8 and sharply decreases at Vr = 2.9 to 3.0. It is noteworthy that the two response curves are exactly the same in the region from Vr = 1.1 to 2.0, where the symmetric vortices are formed, and the alternating vortex flow suppresses the vibration of the cylinder without a splitter plate in the range from Vr = 2.2 to 3.0.
5. Response Characteristics of Cantilevered Cylinders Vibrating with Two Degrees of Freedom
Figure 13(a) shows the response amplitudes ξrms in the stream-wise direction and ηrms in the cross-flow direction against the reduced velocity Vr as the experimental results of vibration of a cantilevered cylinder with a span length of AR = 20 (d = 0.015 m, L = 0.3 m). From this figure, it is clear that the cylinder vibration starts from Vr = 1.25 and reaches a peak at Vr = 2.3 in the first excitation region. As shown in Figure 13(b), the Lissajous figure of vibration of a cylinder at Vr = 2.16 in the first excitation region draws an elongated elliptical trajectory with a dominant large amplitude in the ξ direction and a small amplitude in the η direction. The vibration of the cylinder is suppressed at half of the reduced resonance velocity (Vr = Vrcr/2 = 2.4), and the amplitudes increase again in the higher reduced velocity range. In the second excitation region, the amplitude attains a maximum value at Vr = 3.0, and the Lissajous trajectory draws a figure “8” at Vr = 2.99 in Figure 13(c). In addition, it is noted that the cylinder vibration in the cross-flow direction induced by the so-called vortex excitation can be observed from Vr = 3.5, as shown in Figure 13(a).
However, in the case of a short cylinder with the span length AR = 10, the two-dimensionality of alternating wake vortex flows is weakened by the flow veil over the cylinder tip, and only the first excitation region of the symmetric vortex flow still remains. The values of the wake Strouhal number Stw are locked to 1/4Stc of the Strouhal number of vibrating frequency of the cylinder Stc (=1/Vrcr) at a lower velocity in the first excitation region. Then the value of Stw remains constant, approximately Stw = 0.2 around Vr = 2.5. Furthermore, the value of Stw is locked to 1/2Stc over the region above Vr = 2.25, including the suppression region and the second excitation region.
6. Analysis of Aspect Ratio versus Scruton Number Cn for Cantilevered Cylinders
We analyzed the results of the stream-wise vibration of various circular cylinders and evaluated the critical values of the Scruton number Cn that is able to sufficiently suppress vibration. To compare the response characteristics of various cylinders with different aspect ratios, the maximum amplitudes ξmax (=xmax/d, where xmax is the maximum RMS value of the response amplitude of a cylinder vibrating in the stream-wise direction) with respect to the Cn values are summarized in Figure 14. In the figure, the response characteristics of the two-dimensional cylinder are indicated by solid lines. As Cn increases, the response amplitudes

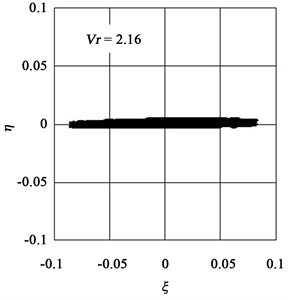

Figure 13. Response amplitude, Strouhal frequency, and Lissajous figures at Vr = 2.16 and Vr = 2.99 for a circular cylinder (AR = 20) vibrating with two degrees of freedom and Cn = 0.97 [17] . (a) The response amplitude and Strouhal frequency; (b) Lissajous figures at Vr = 2.16; (c) Lissajous figures at Vr = 2.99.
Figure 14. Maximum amplitudes of each excitation region for two-dimensional and cantilevered (finite span) cylinders vibrating with one degree of freedom.
ξmax of the first and second excitation regions decrease but exhibit different response characteristics against the Cn values. That is, the maximum amplitude values ξmax sharply decrease against the increase of Cn values in the first excitation region less than Vrcr/2. Meanwhile, the rate of decrease of ξmax against Cn is relatively gentle in the second excitation region, and the value of ξmax becomes as small as 0.005 at Cn = 2.5, which implies that the vibration is suppressed.
The maximum amplitude values ξmax of the cantilevered cylinders of AR = 10 and 21 vibrating with one degree of freedom are shown by symbols against various Cn values in both two excitation regions in Figure 14. It can be seen from this figure that the cantilevered cylinders exhibit response characteristics substantially the same as those of the two-dimensional cylinder in the first excitation region due to the symmetric vortex flow. However, in the second excitation region due to the alternating vortex flow, the ξmax values of the cantilevered cylinders (finite span) decrease more quickly with increasing Cn values, as compared with the curve of the two-dimensional cylinder.
Finally, Figure 15 shows the response characteristics of the cantilevered cylinders vibrating with two degrees of freedom. The response characteristics of the peak ξmax values in the first excitation region are the same as those of the cantilevered cylinders with one degree of freedom in Figure 14, while in the second excitation region, the amplitude depicts a figure “8” trajectory, as shown in Figure 13(c), and is more quickly suppressed with increasing Cn. Therefore, the second excitation region disappears and the first excitation region remains for the cantilevered cylinders of AR < 10. It is noteworthy that the damping rate of vibration of the two-dimensional cylinders is smaller than that of the cantilevered cylinders, which implies that the vibration of two-dimensional cylinders is easily excited.
Figure 15. Maximum amplitudes of each excitation region for cantilevered (finite span) cylinders vibrating with two degrees of freedom.
7. Concluding Remarks
Results from a series of studies on the stream-wise vibration of a circular cylinder that verified Japan Society of Mechanical Engineers Standard S012-1998 were summarized and discussed. Experiments were carried out with a two-dimensional cylinder model and a cantilevered cylinder model with a finite span length. These cylinder models were allowed to vibrate with one degree of freedom in the stream-wise direction. In addition, we employed a cantilevered cylinder model that vibrated with two degrees of freedom in both the stream-wise and cross-flow directions under the same vibration conditions as an actual thermocouple well. The Scruton number Cn was changed over a wide range, so as to evaluate the critical value. For the two-dimensional cylinder, two different types of stream-wise excitations appeared in the range of approximately half of the resonance-reduced velocity. For the stream-wise vibration in the first excitation region due to the symmetric vortex flow, the response amplitudes were sensitive to Cn, while the shedding frequency of alternating vortex flow was locked-in to half of the Strouhal number of vibrating frequency of a cylinder in the second excitation region. When a cantilevered circular cylinder with a finite length vibrates with one degree of freedom in the stream-wise direction, a cylinder with a small aspect ratio has a single excitation region, whereas a cylinder with a large aspect ratio has two excitation regions. Furthermore, the vibration mechanism due to the symmetric vortex flow was investigated by installing a splitter plate in the wake to prevent shedding of alternating vortices. The vibration amplitude of a cylinder with a splitter plate increased surprisingly more than the amplitude of a cylinder without a splitter plate. For a cantilevered cylinder vibrating with two degrees of freedom, the Lissajous figure of vibration of the first excitation region shows the trajectories of elongated elliptical shapes, and in the second excitation region, the Lissajous trajectories draw a figure “8”.
The results and information from these experimental studies demonstrated that Standard S012-1998 is sufficient as a general standard for evaluation of flow-induced vibration of circular cylinders applicable to structures in various industrial fields, including offshore structures, chimneys, and structures in chemical plants and power plants
Acknowledgements
The work described in this paper was mainly based on the research of the flow-induced vibration of bluff bodies that the authors have carried out with former students at Kanazawa University, including Dr. A. Nakamura, Mr. T. Kosugi, Prof. T. Yasuda, Mr. T. Iwasaki, Mr. H. Uchida, Mr. R. Tamaki, Mr. Y. Nagamori, and Mr. F. Matsunaga.
The authors thank Mr. T. Kuratani for his help at Kanazawa University, Prof. K. Matsuda, Dr. S. Saitoh, and Mr. T. Sugimoto (at that time, IHI Co.) for their technical assistance.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Okajima, A. and Kiwata, T. (2019) Flow-Induced Stream-Wise Vibration of Circular Cylinders. Journal of Flow Control, Measurement & Visualization, 7, 133-151. https://doi.org/10.4236/jfcmv.2019.73011
References
- 1. Zdravkovich, M.M. (1998) Flow around Circular Cylinders—Vol. 1 Fundamental, and (2003) Flow around Circular Cylinders—Vol. 2 Applications. Oxford University Press, Oxford. https://doi.org/10.1115/1.2819655
- 2. Sarpkaya, T. (1979) Vortex-Induced Oscillations—A Selective Review. Journal of Applied Mechanics, Transactions ASME, 46, 241-258. https://doi.org/10.1115/1.3424537
- 3. Sarpkaya, T. (2004) A Critical Review of the Intrinsic Nature of Vortex-Induced Vibrations. Journal of Fluids and Structures, 19, 389-447. https://doi.org/10.1016/S0889-9746(04)00035-0
- 4. Bearman, P.W. (1984) Vortex Shedding from Oscillating Bluff Bodies. Annual Review of Fluid Mechanics, 16, 195-222. https://doi.org/10.1146/annurev.fl.16.010184.001211
- 5. Naudascher, E. (1987) Flow-Induced Streamwise Vibrations of Structures. Journal of Fluids and Structures, 1, 265-298. https://doi.org/10.1016/0889-9746(87)90243-X
- 6. Bishop, R.E.D. and Hassan, A.Y. (1964) Lift and Drag Forces on a Circular Cylinder in a Flowing Fluid. The Proceedings of the Royal Society (London) Series A, 277, 51-75. https://doi.org/10.1098/rspa.1964.0005
- 7. Scruton, C. (1965) On the Wind Excited Oscillations of Stacks, Towers, and Masts. Wind Effects on Buildings and Structures, Vol. 2, Her Majesty’s Stationery Office (Proc. Int. Conf. Wind Effects Buildings and Structures (1963)), 798-832.
- 8. Wooton, L.R., Warner, M.H. and Cooper, D.H. (1972) Some Aspects of the Oscillations of Full-Scale Piles. Proceedings of IUTAM-IAHR Symposium, Kuarlsruhe, 14-16 August 1972, 587-601. https://doi.org/10.1007/978-3-642-48279-3_43
- 9. King, R., Prosser, M.J. and Johns, D.J. (1973) On Vortex-Flow Excitation of Model Piles in Water. Journal of Sound and Vibration, 292, 169-188. https://doi.org/10.1016/S0022-460X(73)80133-6
- 10. Japan Nuclear Cycle Development Institute (Formerly PNC) (1997) Proposed Flow-Induced Vibration Design Guide for Thermometer Wells. PNC-TN9410 97-042. (In Japanese)
- 11. Japan Society of Mechanical Engineers (1998) Guideline for Evaluation of Flow-Induced Vibration of a Cylindrical Structure in a Pipe. JSME Standard S012-1998. (In Japanese)
- 12. Okajima, A., Morishita, M., Nishihara, T. and Nakamura, A. (2004) Guideline for Evaluation of Flow-Induced Vibration of a Cylindrical Structure in a Pipe. The 6th International Conference on Nuclear Thermal Hydraulics, Operations and Safety, Nara, 4-8 October 2004, N6P160.
- 13. Okajima, A., Yasuda, T. and Iwasaki, T. (2000) Flow Visualizations of In-Line Oscillation of a Cylinder with a Circular or Rectangular Section. Proceedings of 6th Triennial International Symposium on FLCOME, Sherbrooke, 13-17 August, 1-6.
- 14. Okajima, A., Nakamura, A., Kosugi, T. and Uchida, H. (2002) Flow-Induced In-Line Oscillation of a Circular Cylinder. Proceedings of Conference on Bluff Body, Wake and Vortex-Flow-Induced Vibration, Port Douglas, 17-20 December, 61-64.
- 15. Okajima, A., Nakamura, A., Kosugi, T., Uchida, H. and Tamaki, R. (2004) Flow-Induced In-Line Oscillation of a Circular Cylinder. European Journal of Mechanics B, 23, 115-125. https://doi.org/10.1016/j.euromechflu.2003.09.009
- 16. Okajima, A., Kosugi, T. and Nakamura, A. (2002) Flow-Induced In-Line Oscillation of a Circular Cylinder in a Water Tunnel. Journal of Pressure Vessel Technology, 124, 89-96. https://doi.org/10.1115/1.1430670
- 17. Sugimoto, T., Okajima, A., Kiwata, T., Saitoh, S. and Matsuda, K. (2005) Water Tunnel Experiments on the In-Line Oscillation of Circular Cylinders with Finite Length. Transactions of the Japan Society of Mechanical Engineers, Ser. B, 71, 754-759. (In Japanese) https://doi.org/10.1299/kikaib.71.753
- 18. Nakamura, A., Okajima, A., Kosugi, T., Tamaki, R. and Kiwata, T. (2005) Flow-Induced In-Line Oscillation of a Cantilevered Tapered Circular Cylinder. Transactions of the Japan Society of Mechanical Engineers, Ser. B, 71, 88-95. (In Japanese) https://doi.org/10.1299/kikaib.71.88
- 19. Aguirre, J.E. (1977) Flow-Induced, In-line Vibrations of a Circular Cylinder. Doctoral Dissertation, Imperial College of Science and Technology, London.
Nomenclature
AR = aspect ratio of cylinder, Le/d (-)
Cn = Scruton number (reduced structural mass-damping parameter) 2 mLeδ/ρd2, 2 MLeδ (-)
d = diameter of cylinder (m)
fc = natural frequency of vibrating cylinder in water (Hz)
fn = natural vortex shedding frequency in wake for stationary cylinder (Hz)
fw = vortex shedding frequency in wake (Hz)
l = length of splitter plate (m)
L = total spanlength of cylinder (m)
Le = effective spanlength of cylinder (m)
m = mass per unit total spanlength in water (kg/m)
Re = Reynolds number, Ud/ν (-)
Stc = Strouhal number of vibrating cylinder, fcd/U (-)
Stn = Strouhal number for stationary cylinder, fnd/U (-)
Stw = Strouhal number of vortex shedding frequency in wake, fwd/U (-)
U = uniform flow velocity (m/s)
Vr = reduced velocity, U/fcd (-)
Vrcr = reduced resonance velocity, U/fn d = 1/Stn (-)
xmax = maximum RMS response amplitude of cylinder in stream-wise direction (m)
xrms = root-mean-square (RMS) response amplitude of cylinder in stream-wise direction (m)
yrms = RMS response amplitude of cylinder in cross-wise direction (m)
δ = logarithmic decrement of structural damping parameter in water (-)
ηrms = non-dimensional value of RMS response amplitude of cylinder vibrating in cross-flow direction, yrms/d (-)
ν = kinematic viscosity of working fluid (m2/s)
ξmax = non-dimensional maximum value of RMS response amplitude of vibrating cylinder in the stream-wise direction, xmax/d (-)
ξrms = non-dimensional value of RMS response amplitude of cylinder vibrating in stream-wise direction, xrms/d (-)
ρ = fluid mass density (kg/m3)