Journal of Flow Control, Measurement & Visualization
Vol.03 No.03(2015), Article ID:57931,18 pages
10.4236/jfcmv.2015.33009
Oscillating Water Surface Measurement of Free Overfall with a Plunge Pool
Shun Chung Tsung, Jihn Sung Lai, Hau Wei Wang
Taiwan Typhoon and Flood Research Institute, National Applied Research Laboratories, Taipei, Taiwan
Email: yinwei99@ms26.hinet.net
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 March 2015; accepted 15 May 2015; published 14 July 2015
ABSTRACT
This study presents a laser-sheet imaging technique to measure the water surface of free overfalls with plunge pool. Varying the plunge pool length of a constant approach discharge created skimming, periodic oscillatory, and nappe flows. This study analyzes the resulting oscillating water surfaces and temporal variations of water stages at particular positions in the periodic oscillatory flow condition. The oscillation period and amplitude of temporal water stage variation were determined by directly measuring the time interval and water stage differences in water stage variations, respectively. The plunge pool length and air pocket characteristics seriously affected the periodic oscillatory flow. The oscillation period increased as the plunge pool length increased. On the other hand, the water stage amplitude decreased sharply when the plunge pool exceeded a specific length. The absence of an air pocket beneath the falling nappe significantly increased the oscillation period and decreased the water stage amplitude. This study investigates water surface oscillation in the plunge pool and the upstream side of the drop. However, the mean end depth of a periodic oscillatory flow with an air pocket is also applicable to discharge estimation using the end depth method.
Keywords:
Laser-Sheet Imaging Technique, Free Overfall, Periodic Oscillatory Flow, End Depth

1. Introduction
Researchers frequently use free overfall flow to estimate the discharge or dissipate energy of the approach flow in an open channel. Dey [1] recently provides a review of discharge estimation. The characteristics of flow over a drop with a plunge pool include skimming and nappe flow [2] [3] . Figure 1 shows the characteristic features of skimming and nappe flows, and illustrates the flow direction, and vortical structures in both flow conditions.

Figure 1. Sketch of free overfall flow: (a) skimming flow; (b) nappe flow.
Figure 1(a) shows that skimming flow refers to a falling jet smoothly sliding past the plunge pool to the downstream end due to a large discharge or short plunge pool. The shear of the sliding jet drives a primary clockwise vortex. In nappe flows, the falling jet directly impinges on the plunge pool. Nappe flows normally occur in flows with a low discharge or a long plunge pool (Figure 1(b)). The impinging jet associated with the nappe flow forms two primary vortices. The first of these vortices, called the recirculating pool, occurs near to the vertical drop wall. The second vortex, called the recirculating region, forms above the downstream sliding jet. In both skimming and nappe flows, the water surface, and jet remain relatively steady. However, Lin et al. [3] found that the jet exhibited a switching pattern in certain discharge rates for a constant plunge pool length. The flow in a plunge pool also exhibited an oscillatory pattern.
Many researchers have established the relationship between free overfall flow and flow characteristics by measuring water stages. The water depth at the brink of the drop is called the end depth. The end depth is often measured, and analyzed to obtain the critical depth to estimate the discharge. This technique is called the end-depth method [4] -[18] . Gill [19] , Robinson [20] [21] , Wu and Rajaratnam [23] , Davis et al. [11] , Robinson et al. [24] and Lin et al. [25] measured the water stage at the downstream end of the drop, including the nappe or tail water depth. They focused on the steady water surface and measured its profile using single-point instruments such as a point gauge, pressure transmitter, and wave gauge. However, these tools are unable to track an oscillating water surface because the probes may significantly affect the flow profile. Lin et al. [3] qualitatively illustrated the water surface of a periodic oscillatory flow based on images captured by using a Charge-Coupled Device (CCD), but provided no quantitative data. Researchers often apply imaging or remote sensing methods such as particle imaging velocimetry, particle-tracking velocimetry, and techniques based on shape-from-shad- ing and shape-from-stereo techniques, to velocity field measurements and wave and ocean surface detection. Adrian [26] , Jähne et al. [27] , and Adrian [28] summarized these techniques and corresponding theories. Hereafter considerable methods are still under development. More recently, Nicolas et al. [29] utilized radar to remotely detect surface velocity. Craeye et al. [30] employed an optical technique to indirectly analyze the wave surface using a mirror image. Dabiri and Gharib [31] investigated water surface deformation using a free surface gradient detector technique. Kouyi et al. [32] used the light projection technique to determine the water surface. Douxchamps et al. [33] developed a stereoscopic imaging method based on the particle tracking technique to estimate free surface velocity and elevation. The current study measures the local water stage variations of the oscillatory flow in the plunge pool at a specific position and monitors changes in the water surface profile. A review of the literature referenced above suggests that imaging techniques or remote sensing methods are able to measure and track water surface changes. Therefore, this study adopts an optical imaging method.
Previous studies apply a laser-sheet imaging technique to topographical measurement [34] [35] . Laser-sheet imaging technique is a non-intrusive measurement technique that easily avoids localized effects around a device probe, especially for a rapidly changing flow pattern. In this approach, a video camera films a lighten line located on the surface of the object. The trace of this line is then identified by image processing and coordinate transformation for 2D and 3D measurements, respectively. This technique monitors successive changes in the surface of a target and provides local information for detailed analysis. However, this technique is originally designed for solid surfaces. Following Gardarsson and Yeh [36] , we dyed the water to make it opaque and overcome the problem of laser sheets penetrating the clear water surface. The experiments in this study use a laser-sheet imaging technique and associated image treatments to profile the oscillating water surface of dyed water and analyze the characteristics of oscillatory water surface.
For a flow with oscillatory patterns, the water surface variation is a principal external feature that categorizes different flow conditions and illustrates flow characteristics. Previous studies focus on period and amplitude [3] [30] [37] -[40] . Therefore, this study traces the water surface and analyzes the period and amplitude of the waves. This analysis contributes to define the observed patterns and identify the influence of experimental conditions. The objective of this study is to measure the oscillating water surface of a free overfall flow with plunge pool using the laser-sheet imaging technique. The analyses in this study focus on the flow, period, and amplitude characteristics of the oscillating water surface. The proposed approach estimates the discharge of flow over a drop using steady water surface at upstream and downstream side of the drop, including skimming and nappe flows [1] . Only a few studies examine the applicability of the end depth method for periodic oscillatory flow. This study checks the estimated discharge using the end depth method for periodic oscillatory flow.
2. Experimental Setup
The experiments in this study were conducted in a rectangular horizontal flume measuring 20 cm wide, 25 cm high, and 350 cm long, located at the Hydrotech Research Institute, National Taiwan University. Figure 2 shows the experimental setup. The flume was made of transparent acrylic board to facilitate observation. The flume had a cyclic water supply, and a valve controlled the discharge rate. A honeycomb installed at the flume entrance stabilized the flow.
The proposed model consisted of a vertical drop with a plunge pool near the downstream end of the flume. The height of the drop hd and downstream sill hs were 11 and 5 cm, respectively. The length of the plunge pool Lp was adjustable to create various flow patterns. As Figure 2 indicates, the origin of coordinate system was located at the toe of the vertical wall. The positive x-axis and z-axis pointed toward the downstream side and water surface, respectively. The model in this study used one approach discharge, Qi = 2620 cm3/s, and the corresponding water depth was 2.7 cm at x = −60 cm. The Froude number was 0.94, that is, the upstream approach flow was a subcritical flow.
The formation of an air pocket under the falling nappe depends on experimental control and conditions in the plunge pool. Most of the experiments were performed with either ventilation (i.e., atmospheric pressure in the air pocket) or exhaustion (i.e., no air pocket). The experiments in this study did not ventilate or exhaust the air pocket in all tests. Preliminary tests were first conducted for empty and full plunge pools. Both cases give different flying distance in height. Figure 3 clearly shows two distinct air pocket shapes beneath the falling nappe for different conditions in the plunge pool at Lp = 25 cm (i.e., the nappe flow). Figure 3(a) reveals a shorter and
Figure 2. Sketch of flume, coordinate system and definitions of model dimension: drop height hd = 11 cm, sill height hs = 5 cm, and plunge pool length Lp.
wider air pocket when the plunge pool is empty before experiment, while Figure 3(b) shows a longer and narrower air pocket when the plunge pool filled with water before experiment. To standardize experimental operation and match field situations, the plunge pool was filled with water before each run.
The main task of this study is to measure water surface oscillation. To determine the plunge pool length for periodic oscillatory flow before measurements, several experiments with Lp = 5 to 30 cm were conducted to determine flow features. The flow patterns are visually categorized according to variations in the water surface in the plunge pool. Figure 4 shows snapshots of skimming, periodic oscillatory, and nappe flows. Skimming flow refers to the falling nappe sliding over the plunge pool at Lp = 5 cm as Figure 4(a) illustrates. When Lp > 14.5 cm, the falling jet starts to switch in the plunge pool. For example, at Lp = 17 cm, skimming (Figure 4(b)) and nappe (Figure 4(c)) flows periodically alternate with each other. This oscillatory water surface phenomenon continues until Lp = 20.5 cm. The periodic oscillatory flow ranges from 14.5 ≤ Lp ≤ 20.5 cm. Figure 4(d) shows the nappe flow in which the falling jet directly impinges on the plunge pool.
This study uses a point gauge and the laser-sheet imaging technique to measure the steady and oscillating water surfaces. The point gauge was modified from a commercial vernier spectrometer, with an approximate accuracy of ± 0.1 mm. Figure 5(a) shows that the experimental apparatus for the laser-sheet imaging technique consists of a laser sheet and an image sensor. A red laser sheet of 5 mW was mounted on a steel frame and vertically projected to cover a length of 35 cm. The water was dyed opaque and white before experiments to allow the

Figure 3. Comparisons of air pocket under various conditions in the plunge pool before experiment: (a) empty plunge pool; (b) plunge pool filled up with water.


Figure 4. Photos of free overfall flow: (a) Lp = 5 cm, skimming flow; (b) and (c) Lp = 17 cm, skimming and nappe flow conditions of periodic oscillatory flow; (d) Lp = 25 cm, nappe flow.

Figure 5. Sketch of the laser-sheet imaging technique: (a) experimental setup; (b) mesh board for camera calibration.
water surface to reflect the laser sheet. The viscosity of the dyed water was almost equal to clean water. The illuminated water surface was filmed using an image sensor located at the side of the flume with an oblique angle of about 45 degrees. Filming was performed in a darkroom to highlight the water surface illuminated by the laser sheet. The image sensor used in this study was a TRV 17 Sony DV camera operating in an interlaced mode at a frequency of 30 Hz. The interlaced image had a resolution of 640 × 480 pixels.
3. Laser-Sheet Imaging Technique
This section presents the details of operation steps of the laser-sheet imaging technique. The water surface images were first identified by 2D positioning method and the spatial positions were then determined using camera calibration and coordinate transformation. Additionally, a regression method was employed to discard unreasonable data and obtain a smooth water surface profile. Measured water stage modification was performed to modify the measurement error due to presentation of light on water surface.
3.1. Water Surface Positioning on the 2D Image
All image analyses to position the water surface were performed off-line and automatically. Digital images were extracted from the image sensor and then de-interlaced from 640 × 480 to 640 × 240 pixels. In the raw 2D image, the water surface appears as a bright stripe of high-intensity pixels, as Figure 6(a) shows. The following methods were executed to identify these pixels. Each image was first convoluted with a Gaussian mask to reduce noise. Figure 6(b) shows the blurred image after noise reduction. The blurred images were then convoluted using a Laplacian-of-Gaussian mask to highlight the illuminated pixels [41] . Figure 6(c) demonstrates the high gray contrast between the bright stripe and its background. This image processing technique facilitated subsequent object identification. However, some bright spots, called outliers, appeared beyond the bright stripe due to random reflection of the laser sheet. A certain intensity threshold was used to select the local brightest pixels and their positions were refined to sub-pixel accuracy using quadratic fit. A tenth of the highest intensity on each image served as the threshold. Figure 6(d) denotes the identified pixels with a plus sign along the bright stripe. However, several outliers remained. A method in section 3.3 will be introduced to remove outliers and interpreted in the following section. For more details on this 2D image positioning method, refer to Capart et al. [42] .
3.2. Camera Calibration and Coordinate Transformation
The pixels of water surface on the images are marked using the processes of 2D positioning. The camera calibration between image and spatial coordinate was performed to determine the real spatial positions of water surface. Figure 5(b) depicts this apparatus. A meshed board was placed at y = 0, 5 and −5 cm to provide complete information on 3D coordinates, although the center line of the flume requires a 2D water surface. To completely cover the measurement area, the length of the board was 60 cm, including 20 cm and 40 cm for the upstream and downstream sides of the drop. The image sensor had the same location and viewing angle as the running experiment. The captured images for camera calibration were then extracted from the image sensor and de-interlaced in vertical resolution.


Figure 6. Algorithm of water surface positioning: (a) raw 2D image extracted from digital camera; (b) after convolution with Gaussian mask; (c) after Laplacian-of-Gaussian mask; (d) obtained water surface marked in plus sign.
For each case, at least 15 calibration points were selected from the meshed board to cover the measurement area. Their known 2D image and 3D spatial coordinates were recorded and denoted as
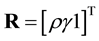 and
and , respectively. The terms ρ and γ denote the row and column in the image, respectively. The relationship between image and spatial coordinate appears as a linear form, known as affine transformation.
, respectively. The terms ρ and γ denote the row and column in the image, respectively. The relationship between image and spatial coordinate appears as a linear form, known as affine transformation.
 . (1)
. (1)
where α is a free parameter. The matrix A and b are parameters of the relationship between R and r. Figure 7 shows the geometry of the projection from the image coordinate to the spatial coordinate. Substituting the R and r of all calibration points into Equation (1) leads to

where C is a matrix including unknown A and b, and



where the subscript index i represents the number of calibration points used. The lowercase letter a and b are the components of matrix A and b. The term




where




Figure 7. Geometry of imaging configuration between image and spatial coordinate.
3.3. Measured Water Stage Modification
The positions of the marked pixels on the image using 2D positioning process were transformed from the image to spatial coordinate. However, the resulting positions were not ordered because the 2D positioning process is based on the intensity of brightness. Therefore, we sorted the resulting spatial positions by longitudinal distance from the brink (i.e., x position) to execute the following post-process.
Figure 6(d) shows several outliers due to the random reflection of the laser sheet. These outliers caused errors in the water surface, corrupting water stage analysis. This study adopts a local regression method, robust Loess, to remove these outliers and obtain a smooth water surface [43] . Loess is an outlier resistant method based on local polynomial fits for bivariate data. The code in the smooth toolbox of MATLAB was directly employed [44] . The local regression in this study applies weighted linear least squares and a 2nd degree polynomial model. The selected span of data for local regression was 10%, or 1/10 of the data near each treated datum. This method assigns a zero weight to data more than six times of the mean absolute deviation, and discards any remaining outliers.
A final test of the laser-sheet imaging technique was performed in a still rectangular tank placed in the plunge pool and filled with dyed water. The previous processes, including 2D positioning, coordinate transformation, outlier filtering, and smoothing the obtained water surface, were repeated. This test revealed that the original detected water surface was slightly lower than the actual water surface because the laser sheet penetrated the water. Therefore, we tuned the positions of the marked pixel in the 2D image until the transformed spatial positions matched the actual water stage measured using a point gauge. The overall deviation from the test between the original measured and actual water stage in the tank for all cases in this study was approximately 2.5 mm, that is, 3 pixels in vertical direction on 2D image. Each original detected water surface was adjusted based on these test results.
3.4. Validation and Error Estimation
To validate the laser-sheet imaging technique applied to water surface measurement, two tests were carried out to steady water surface profile with Lp = 5 and 25 cm. These tests indicate a skimming and nappe flow, respectively.
Due to the power limitation of laser, the clear laser line on the water was about 35 cm. For case of Lp = 5 cm, the measurement range was x = −10 - 25 cm. For the case of Lp = 25 cm, ripples appeared near the recirculation region and sill of the plunge pool. To check the accuracy of the measurement near these two areas, the laser sheet was shifted to cover the area from x = 10 to 30 cm. The duration of videotaping was 30 seconds for each case, producing 900 images. In addition, the water stages in all these cases were measured using point gauge as benchmarks, which are the average values of 3-time measurements. The point gauge is a popular tool with sharp stick and vernier to measure water surface level in physical model tests. The measured water stages were also modified based on the test results of still dyed water with known water stage (Section 3.3). The measured data for each case were treated using the robust Loess method to smooth the measured water surface profiles. Figure 8 compares the measured water surface profile using the point gauge and the laser-sheet imaging technique, showing good agreement between both measurements. The root-mean-square of deviations between both measurements for cases of Lp = 5 cm and Lp = 25 cm were 0.23 and 0.18 cm, respectively. The relative error in the vertical direction was approximately 0.8%.

Figure 8. Comparisons of measured surface profiles using point gauge (hollow dots) and the laser- sheet imaging technique (lines): (a) Lp = 5 cm, skimming flow; (b) Lp = 25 cm, nappe flow.
4. Results and Discussions
This section focuses on the characteristics of periodic oscillatory flow condition. The following subsections first describe the patterns of oscillating water surface profile (Section 4.1). Section 4.2 and 4.3 further discuss the oscillation period and water stage amplitude of periodic oscillatory flow varying with various Lp at various x-positions. The oscillation period, denoted as T, presents the time span of recurrence in water stage changes. The water stage amplitude, denoted as Am, presents the height between the maximum and minimum water stage in a periodic oscillatory flow. Finally, Section 4.4 applies the end depth method to the discharge measurement of periodic oscillatory flow.
4.1. Descriptions of Oscillating Water Stage
The flow pattern changed from a skimming flow to a nappe flow as the length of the plunge pool increased. According to visible observations, a periodic oscillatory flow occurred between Lp = 14.5 and 20.5 cm, in which the water stage in the plunge pool regularly varied up and down. This flow pattern alternately exhibited skimming and nappe flow characteristics. Moreover, the impinging jet periodically migrated between the bed of the plunge pool and the vertical wall of the sill. Figures 9(a)-(d) present snapshots of the flow condition variations for Lp = 17 cm at 3.4, 4.0, 4.3 and 4.7 seconds. Figure 9(a) reveals the skimming flow condition at t = 3.4 sec. In this case, the nappe rose and the sliding jet smoothly slid cross the plunge pool. The nappe immediately fell down and the water surface formed a concave shape in the middle of the plunge pool at t = 4.0 sec, as Figure 9(b) shows. Additionally, the water surface near the vertical wall of sill rose and moved toward upstream, like a surge. Figure 9(c) illustrates a sliding jet submerged by the upstreamward moving surge at t = 4.3 sec. In this case, obvious and strong aeration occurred, producing large bubbles. The nappe began impinging on the plunge pool and the flow gradually changed into the nappe flow conditions shown in Figure 9(d) (t = 4.7 sec). Two evident vortical structures visualized by bubbles appeared beside the impinging jet: the recirculating pool and recirculating region. The continual accumulation of water under the nappe caused it to rise and eventually occupy the entire plunge pool. On the other hand, the support beneath the nappe was insufficient to resist the gravity of the nappe. The nappe consequently fell down again.
Figures 9(e)-(h) show the corresponding measured water surfaces at Lp = 17 cm using the laser-sheet imaging technique. Measurements (lines) give good agreement with the snapshots. The robust Loess method easily discards the outliers marked in the circle (e.g., those in Figure 9(e)). These comparisons suggest that the laser-sheet image technique is appropriate to obtain oscillating water surface profile of a free overfall flow. The measured oscillating water surface indicated several interesting features. For skimming flow condition, Figure 9(e) shows a smooth profile from the drop until x = 12 cm, near the sill. Ripples appeared at the downstream end. As the nappe fell, the profile shows a semicircle-like concave profile forming in the plunge pool, as Figure 9(f) illustrates. Moreover, the water surface profile stage near the vertical wall of the sill remained uneven. Figure 9(g) shows a clear border at x = 5 cm, that is, the position of falling jet impinged on the water. However, at this moment, the surge coming from the sill mixed with the sliding jet. In contrast, Figure 9(d) clearly shows the nappe flow condition. The corresponding measured water surface (Figure 9(h)) also clearly reveals the falling jet (x =




Figure 9. Photos of periodic oscillatory flow of Lp = 17 cm and corresponding measured water surface profiles using the laser-sheet imaging technique: (a), (e) nappe rising and crossing over the plunge pool [t = 3.4 s]; (b), (f) nappe falling and surge moving backward [t = 4.0 s]; (c), (g) strongly mixing with air after nappe collapsing [t = 4.3 s]; (d), (h) nappe impinging into plunge pool [t = 4.7 s]. Circled data in panel e are examples of outliers beyond presented water surface profile.
0 - 7 cm), re-circulating region (x = 7 - 12 cm) and hydraulic jump (x = 12 - 24 cm) induced by the sliding jet flow along the vertical sill wall. These observations indicate that the hydraulic jump is more apparent in the nappe flow condition of the periodic oscillatory flow.
Figure 10 shows the detailed spatial and temporal variations in the measured water surface for Lp = 17 cm. This figure gave results of one measurement due to dynamic flow patterns. The water surfaces piled up from the
Figure 10. Temporal and spatial measured water surfaces of Lp = 17 cm from t = 3.4 to 7.4 sec staggered at 0.1 sec time interval.
bottom to the top of the figure staggered at time intervals of 0.1 sec. The duration t = 3.4 - 7.4 seconds cover one cycle of variation. The water surface shows a skimming flow condition at t = 3.4 sec, and the fluent water surfaces from the drop indicate a sliding jet. In this figure, the nappe falls as time progresses. The concave slope in the plunge pool and hydraulic jump around the downstream vertical sill become apparent. Both of these features moved upstream, as indicated by t = 3.4 - 4.2 sec. The minimum water stage in the plunge pool occurred at t = 4.0 sec. Beyond this point, the water surface gradually becomes relatively flat, both in the plunge pool and around the vertical sill, due to the submergence of the nappe by the upstream moving hydraulic jump from t = 4.0 - 4.6 sec. In the meantime, the nappe flow condition continued to develop. During t = 4.7 - 6.1 sec, the hydraulic jump around the vertical sill formed again. At this stage, the flow exhibited nappe flow conditions. After t = 6.1 sec, the falling jet began to stretch downstream. The original hydraulic jump around the sill migrated downstream and the water surface turned flat until t = 6.8 sec, completing a full cycle of periodic oscillatory flow. In summary, these observations suggest that the composition of water surfaces in the plunge pool and around the vertical sill clearly reveals the development between skimming and nappe flow conditions. In addition, the time interval is nearly 0.9 sec (t = 3.4 - 4.3 sec) for skimming flow condition in a cycle. On the other hand, the remaining time 2.5 sec, nappe flow condition is exhibited. This suggests that at Lp = 17 cm, the skimming flow condition is maintained for a rather short time.
4.2. Oscillating Water Stage and Characteristic Estimation
The laser-sheet imaging technique accurately profiles oscillating water surfaces, making it easy to extract the changing water depth at any specific position for further analysis. Figure 11 illustrates the histories of water stages at x = 5, 10 and 20 cm for Lp = 17 cm. The three water depth variations in this figure give apparently different periodic patterns due to the effect of flume geometry. At x = 5 cm, Figure 11(a) exhibits even variation, since the observed position is located at the falling jet. Figure 11(b) (at x = 10 cm) shows a jagged water stage history because the position is the concave (see Figure 9(b) and Figure 9(f)) and recirculating regimes (see Figure 9(d) and Figure 9(h)). This situation leads to obvious differences of water stage between the maximum and minimum water stage at x = 10 cm. It is easy to recognize the periodic pattern at x = 5 and 10 cm. Nevertheless, the periodicity becomes less obvious at positions far from the plunge pool, as Figure 11(c) shows. This
Figure 11. Time history of water stages measured using laser-sheet image technique at positions (a) x = 5 cm, (b) x = 10 cm and (c) x = 20 cm. Plunge pool length is Lp = 17 cm and gray zone marks a cycle of oscillation. The two-letter word means panel numbers in Figure 9.
suggests that the best position for detecting the periodic characteristic of a free overfall flow is within the plunge pool.
To link the water depth variations and periodic oscillatory flow conditions, a gray area is superimposed onto Figure 11(b) (at x = 10 cm). Figure 9 shows the corresponding times. A two-letter index presents two panels in Figure 9. For example, the index ae means panel a and e in Figure 9. The index ae, which shows the highest water stage, exhibits a skimming flow condition in a periodic oscillatory flow. As time increases, the water depth decreases sharply, i.e., the nappe starts to fall. The lowest stage, index bf, formed at t = 4 sec when a semicircle-like concave formed. The segment between bf and cg reveals the rapid rise of the water stage due to a backward hydraulic jump covering the sliding jet. In this case, the nappe directly impinged on the plunge pool and the flow exhibited nappe flow conditions from index dh. Based on the temporal development of the water stage with Lp = 17 cm, the duration of skimming flow conditions was relatively short compared with the nappe flow conditions.
The flow pattern in the plunge pool oscillated periodically, while the water stage at the upstream side of the drop seems steady. However, the upstream side still exhibited temporal development of the oscillatory pattern. Figure 12 shows the histories of measured water depth at x = 0, −2 and −5 cm. Figure 12(a) and Figure 12(b) (x = 0 and −2 cm) clearly shows periodic oscillation. The oscillation period (T) in the water stage is similar to that in the plunge pool, but its amplitude (Am) is significantly less than that in the plunge pool. In addition, the amplitude decreased as the measured position moved upstream, eventually dying out. At x = −5 cm for Lp = 17 cm, Figure 12(c) shows that the water stage revealed no oscillatory pattern, and only random noise. The observed phenomena clearly indicate that the oscillatory pattern propagated both downstream and upstream.
To better understand the characteristics of the oscillating water surface, this study measures and discusses the oscillation period (T) and water stage amplitude (Am) for various plunge pool lengths and at various positions. The experiments in this study directly measured each time interval of two adjacent crests and troughs of water stage history, and then used the average values as the oscillation period (T). Similarly, the average of the water stage differences between each neighboring crest and trough represents the water stage amplitude (Am). The local crests and troughs were automatically identified. Table 1 shows the measured oscillation periods (T) for Lp = 14.5 - 20.5 cm at x = 5 and 10 cm (column 2 and 3), including tests conducted in the absence of an air pocket with Lp = 14.5 and 15 cm. The values of oscillation periods (T) at x = 5 and 10 cm for each plunge pool length are similar. This table clearly shows that the oscillation periods (T) increased with increasing Lp. In addition,
Figure 12. Time history of measured water stages at upstream side of the drop: (a) x = 0 cm, (b) x = −2 cm; (c) x = −5 cm. Plunge pool length is Lp = 17 cm.
Table 1. Comparisons of oscillation periods obtained from direct measurements, FFT analysis and Lin’s regression (Superscript “*” denotes the absence of air pocket beneath the falling nappe).
oscillation periods (T) increased as the air pocket disappeared for Lp = 14.5 and 15 cm.
This study includes Fast Fourier Transform (FFT) frequency analysis to validate the proposed method. Column 4 in Table 1 lists oscillation periods obtained from FFT analysis. The deviations in the results of the direct measurement and FFT are less than 0.1 second. These results indicate that the proposed method is a simple and accurate way to obtain the oscillation period of the water stage in the plunge pool of free overfall flow. Lin et al. [3] measured single-point water stage in the plunge pool with various ratios of sill height to drop height, hs/hd, = 0.25 ? 0.71. A regression of oscillation frequency was then determined to be a function of drop height (hd), sill height (hs), critical velocity of approach flow (uc), plunge pool length (Lp) and gravity (g). The hs/hd ratio in this study is 0.45, proving that Lin’s regression is adequate. Column 5 in Table 1 shows the regressive oscillation period using Lin’s regression, revealing considerable deviation between measured and computed data. The regressive oscillation periods from Lp = 14.5 to 19 cm are longer than the measured ones. On the other hand, the estimated oscillation periods for Lp = 20 and 20.5 cm are shorter than the measured periods. The disagreement is primarily due to the absence of an air pocket in Lin’s experiments.
4.3. Period and Amplitude of Oscillating Water Stage
In the periodic oscillatory flow of free overfall flow, the characteristics of flow, involving oscillation period (T) and water stage amplitude (Am), are significantly varied with positions and length of the plunge pool. Figure 13 and 14 exhibit variations in the relationships of T and Am with position x and Lp. In these two figures, the solid symbol represents an air pocket under the nappe, whereas the hollow symbol denotes the absence of an air pocket.
Figure 13(a) shows the oscillation periods at several x positions for various Lp and data within x = −2 and 25 cm. The observed oscillation periods suggest that the free overfall is a system with the same oscillation period in both the upstream and downstream sides of the plunge pool. This information indicates that the oscillation period can be measured at any arbitrary position between x = −2 and 25 cm. However, there are slight differences
Figure 13. Variations of measured (a) oscillation period and b) water stage amplitude for various plunge pool lengths along the flume (x-axis). Symbol: square ■, Lp = 14.5 cm; triangle ▲, Lp = 15 cm; pentagram ★, Lp = 16 cm; circle ●, Lp = 17 cm; diamond ◆, Lp = 18 cm; hexagram, Lp = 19 cm; reversed triangle ?, Lp = 20 cm; right-orient triangle, Lp = 20.5 cm. Solid and hollow symbol denotes with and without air pocket beneath nappe, respectively.
between x = 10 - 20 cm for Lp = 20 and 20.5 cm due to weak nappe oscillations and random high ripples in the recirculating region, which make it difficult to identify the stage crest or trough.
Figure 13(b) illustrates variations of water stage amplitude (Am) along the flow direction in the range of x = −2 - 25 cm. The water stage amplitude at the upstream side of the drop is certainly lower than that at downstream. When an air pocket existed beneath the falling nappe, the water stage amplitude monotonically increased between x = 0 - 7 cm, where the falling jet locates at. The maximum water stage amplitude for each case appears in the interval of x = 8 - 10 cm, where the concave water surface in the plunge pool is found. At x > 10 cm, the water stage amplitude generally decreased. However, variations of the water stage amplitudes along the x-direction reveal distinct features for various Lp. As Lp lengthens, the Am at x = 15 cm decreases, and the Am gradually increases at x = 25 cm. These phenomena are due to recirculating region gradually covering the sliding jet at the range of x = 15 - 20 cm. In this case, it is not clear if the sliding jet stretched and then crossed the plunge pool. For Lp = 20 and 20.5 cm, the water stage amplitudes at x = 25 cm are higher than that at x = 15 and 20 cm. This is because the sliding jet hit different elevations on the vertical wall of the sill, inducing regular water stage variations at the downstream side of the sill. Table 2 lists the detailed data of water stage amplitude, and marks the maximum magnitude for each Lp in bold font.
Figure 13(b) exhibits the variations in water stage amplitude along the x position for Lp = 14.5 and 15 cm without an air pocket. The air pocket has a significant influence on the water stage amplitude. The water stage amplitudes completely diminish, that is, the water surface oscillation becomes weak as the air pocket disappears. The most obvious reduction appears at x = 10 cm, where the original maximum water stage amplitude appears in the presence of an air pocket. Table 2 shows that the decreases in water stage amplitude for Lp = 14.5 and 15 cm exceed 3.0 cm at x = 10 cm. In the absence of an air pocket, the falling jet impinging on the plunge pool from the drop is relatively short. Therefore, the stretching nappe has difficulty pushing the recirculating region across the plunge pool. The backward surge quickly submerges the falling nappe, causing slight changes in the water stage at this point. In addition, the maximum water stage amplitude shifts to positions of x = 15 and 20 cm for Lp = 14.5 and 15 cm, respectively.
The following discussion analyzes another aspect of oscillatory patterns varying with Lp. Figure 14(a) shows
Table 2. The data of water stage amplitude Am at selected positions for each case (Superscript “*” denotes the absence of air pocket beneath the falling nappe; value in bold type means the maximum Am for each Lp; value marked in gray presents the maximum Am for each selected x).
Figure 14. Variations of measured (a) oscillation period and (b) water stage amplitude with plunge pool length at different positions. Symbol: square ■, x = −2 cm; triangle ▲, x = −1 cm; circle ●, x = 0 cm; diamond ◆, x = 5 cm; reversed triangle ?, x = 10 cm; right-orient triangle, x = 15 cm. Solid and hollow symbol denotes with and without air pocket beneath nappe, respectively.
the oscillation period (T) against the plunge pool length (Lp) at x = −2, −1, 0, 5, 10 and 15 cm. This figure shows that the oscillation period is nearly directly proportional to the plunge pool length. This is primarily because the accumulated water volume in the plunge pool required to raise the nappe to form a skimming flow condition increases as the plunge pool length increases. The corresponding required time also increases. The shortest and longest oscillation period were 2.63 and 5.81 seconds, respectively, for Lp = 14.5 and 20.5 cm. In summary, the plunge pool length strongly influenced the oscillation period. In the absence of air pocket, the oscillation period was longer than that with air pocket. For example, the oscillation period increased from 2.75 to 3.19 seconds for Lp = 15 cm. The reason for this oscillation period extension is that the required space beneath the falling nappe for water accumulation to form the skimming flow condition includes the space of the original air pocket.
Figure 14(b) shows how the water stage amplitude changes at different particular positions, including upstream and downstream side of the drop with Lp. The water stage amplitudes at the upstream side of drop are much less than those at the downstream side (see Figure 12(b)). Furthermore, their variations against Lp are insignificant. As shown in Table 2 (column 1, x = 0), overall, the water stage amplitudes in the plunge pool remained approximately the same between Lp = 14.5 - 19 cm but revealed a sharp decrease where Lp > 19 cm. This indicates the effect of Lp on water stage amplitude at a particular position. However, there are discrepancies in water stage amplitude at the downstream side of the drop at different positions. The maximum Am deviates for each Lp. Figure 13(b) shows that the maximum Am for each Lp occurs at x = 8 - 10 cm. However, for a particular position, the maximum occurs at different Lp. For instance, the maximum Am at x = 5, 10 and 15 cm occur at Lp = 16, 18 and 15 cm, respectively (see Table 2). This suggests a direct relationship between variations in the water stage amplitude Am with Lp at different measured positions.
As observed before, the absence of air pocket results in relative small water stage amplitude for Lp = 14.5 and 15 cm. Figure 14(b) shows the water stage amplitude at x = 5 and 10 cm for Lp = 15 cm, decay 0.93 and 3.42 cm, respectively, as air pocket vanishes (see Table 2). This figure indicates the influence of the air pocket on the water stage amplitude and deviated difference at various measured positions.
4.4. Discharge Estimation
Researchers often use free overfall as a means for discharge measurement via steady water depth at the drop, ye. This method is suitable for stable skimming and nappe flows, but may not be suitable for periodic oscillatory flow due to oscillating water depth at the drop (x = 0 cm). Further examination is necessary.
The critical depth yc was derived from the measured end depth ye if the end-depth-ratio (EDR), ye/yc, is known. The discharge was then obtained by
5. Conclusions
This study developed a laser-sheet imaging technique to successively measure water surface of periodic oscillatory flow condition of free overfall with a plunge pool of various lengths. The experiments in this study were conducted in a horizontal flume with 11 cm high drop and 5 cm high sill. All experiments used a constant discharge of 2620 cm3/s, and flow conditions were controlled by adjusting the plunge pool length. Images of the water surfaces illuminated by a laser sheet were captured at regular intervals using a digital camera. The water surfaces were profiled by water surface positioning on acquired images, camera calibration, coordinate transformation, and water stage modification. The water surface measurements were validated using steady water measurements. The relative errors of steady water surface measurements using the laser-sheet imaging technique were approximately 0.8%. The successive oscillating water surface and water stage history at specific positions were extracted from measurement data. The average oscillation period and water stage amplitude at a particular position were obtained by measuring the time interval between adjacent wave crests and height between wave crest and trough, respectively. The proposed method was validated using the FFT scheme, and the mean deviation was nearly 0.05 sec. Overall, the proposed laser-sheet imaging technique provided accurate measurement of water surface profiles.
Periodic oscillatory flow occurred in a particular range of plunge pool length, Lp = 14.5 - 20.5 cm. The
Table 3. Measured end depths and discharge estimations; the exact approach discharge is 2620 cm3/s; Superscript “*” denotes the absence of air pocket beneath the falling nappe and gray zone marks periodic oscillatory flow.
skimming and nappe flow condition appeared alternatively in this kind of flow. The water stage in the plunge pool regularly varied up and down at constant time intervals due to the water accumulation under the sliding jet and gravitation of the sliding jet. This oscillatory phenomenon appeared at upstream side of the drop, in addition to the plunge pool and downstream side. An analysis of temporal water stage variations illustrated that the plunge pool length significantly influenced the oscillation period and water stage amplitude. The oscillation period gradually extended as the plunge pool length increased. The water stage variations and amplitudes at different observed positions exhibited various patterns, and sharply decreased when Lp > 19 cm. The air pocket beneath the falling nappe powerfully affected the behaviors of oscillation period and water stage amplitude of periodic oscillatory flow. In this study, the air pocket disappeared at two particular plunge pool lengths of periodic oscillatory flow, Lp = 14.5 and 15 cm. The disappearance of the air pocket apparently extended the oscillation and noticeably decreased the water stage amplitude. Finally, the mean water depth at the drop served as the end depth in periodic oscillatory flow and the end depth method was then examined. The most of the errors in discharge estimation using the end depth method were less than 5%, suggesting that this method was applicable to periodic oscillatory flows except those without air pockets.
Cite this paper
Shun ChungTsung,Jihn SungLai,Hau WeiWang, (2015) Oscillating Water Surface Measurement of Free Overfall with a Plunge Pool. Journal of Flow Control, Measurement & Visualization,03,87-105. doi: 10.4236/jfcmv.2015.33009
References
- 1. Dey, S. (2002) Free Overfall in Open Channels: State-of-the-Art Review. Flow Measurement and Instrumentation, 13, 247-264. http://dx.doi.org/10.1016/S0955-5986(02)00055-9
- 2. Chanson, H. (1994) Comparison of Energy Dissipation between Nappe and Skimming Flow Regimes on Stepped Chutes. Journal of Hydraulic Research, 32, 213-218. http://dx.doi.org/10.1080/00221686.1994.10750036
- 3. Lin, C., Hsieh, S.C., Kuo, K.J. and Chang, K.A. (2008) Periodic Oscillation Caused by a Flow over a Vertical Drop Pool. Journal of Hydraulic Engineering, 134, 948-960.
http://dx.doi.org/10.1061/(ASCE)0733-9429(2008)134:7(948) - 4. Rouse, H. (1936) Discharge Characteristics of the Free Overfall. Civil Engineering, 6, 257-260.
- 5. Rajaratnam, N., Muralidhar, D. and Beltaos, S. (1976) Roughness Effects on Rectangular free Overfall. Journal of the Hydraulics Division, 102, 599-614.
- 6. Keller, R.J. and Fong, S.S. (1989) Flow Measurement with Trapezoidal Free Overfall. Journal of Irrigation and Drainage Engineering, 115, 125-136.
http://dx.doi.org/10.1061/(ASCE)0733-9437(1989)115:1(125) - 7. Ferro, V. (1992) Flow Measurement with Rectangular Free Overfall. Journal of Irrigation and Drainage Engineering, 118, 956-964. http://dx.doi.org/10.1061/(ASCE)0733-9437(1992)118:6(956)
- 8. Marchi, E. (1993) On the Free Overfall. Journal of Hydraulic Research, 31, 777-790.
http://dx.doi.org/10.1080/00221689309498818 - 9. Bhallamudi, S.M. (1994) End Depth in Trapezoidal and Exponential Channels. Journal of Hydraulic Research, 32, 219-232. http://dx.doi.org/10.1080/00221689409498725
- 10. Sturm, T.W. and Sadiq, A. (1996) Water Surface Profiles in Compound Channel with Multiple Critical Depths. Journal of Hydraulic Engineering, 122, 703-709. http://dx.doi.org/10.1061/(ASCE)0733-9429(1996)122:12(703)
- 11. Davis, A.C., Jacob, R.P. and Ellett, B.G.S. (1999) Estimating Trajectory of Free Overfall Nappe. Journal of Hydraulic Engineering, 125, 79-82. http://dx.doi.org/10.1061/(ASCE)0733-9429(1999)125:1(79)
- 12. Ferro, V. (1999) Theoretical End-Depth-Discharge Relationship for Free Overfall. Journal of Irrigation and Drainage Engineering, 125, 40-44. http://dx.doi.org/10.1061/(ASCE)0733-9437(1999)125:1(40)
- 13. Sterling, M. and Knight, D.W. (2001) The Free Overfall as a Flow-Measuring Device in a Circular Channel. Proceedings of the ICE—Water and Maritime Engineering, 148, 235-243.
http://dx.doi.org/10.1680/wame.2001.148.4.235 - 14. Ramamurthy, A.S., Zhai, C. and Qu, J. (2004) End Depth-Discharge Relation at Free Overfall of Trapezoidal Channels. Journal of Irrigation and Drainage Engineering, 130, 432-436.
http://dx.doi.org/10.1061/(ASCE)0733-9437(2004)130:5(432) - 15. Dey, S. (2005) End Depth in U-Shaped Channels: A Simplified Approach. Journal of Hydraulic Engineering, 131, 513-516. http://dx.doi.org/10.1061/(ASCE)0733-9429(2005)131:6(513)
- 16. Dey, S. and Lambert, M.F. (2006) Discharge Prediction in Compound Channels by End Depth Method. Journal of Hydraulic Research, 44, 767-776. http://dx.doi.org/10.1080/00221686.2006.9521727
- 17. Tigrek, S., Firat, C.E. and Ger, A.M. (2008) Use of Brink Depth in Discharge Measurement. Journal of Irrigation and Drainage Engineering, 134, 89-95.
http://dx.doi.org/10.1061/(ASCE)0733-9437(2008)134:1(89) - 18. Sharifi, S., Sterling, M. and Knight, D.W. (2011) Prediction of End-Depth Ratio of Open Channels Using Genetic Programming. Journal of Hydroinformatics, 13, 36-48.
http://dx.doi.org/10.2166/hydro.2010.087 - 19. Gill, M.A. (1979) Hydraulics of Rectangular Vertical Drop Structures. Journal of Hydraulic Research, 17, 289-302. http://dx.doi.org/10.1080/00221687909499573
- 20. Robinson, K.M. (1989) Stress Distribution at an Overfall. Transactions of the ASAE, 32, 75-80.
http://dx.doi.org/10.13031/2013.30965 - 21. Robinson, K.M. (1989) Hydraulics Stresses on an Overfall Boundary. Transactions of the ASAE, 32, 1269-1274. http://dx.doi.org/10.13031/2013.31144
- 22. Robinson, K.M. (1992) Predicting Stress and Pressure at an Overfall. Transactions of the ASAE, 35, 561-569. http://dx.doi.org/10.13031/2013.28634
- 23. Wu, S. and Rajaratnam, N. (1998) Impinging Jet and Surface Flow Regimes at Drop. Journal of Hydraulic Research, 36, 69-74. http://dx.doi.org/10.1080/00221689809498378
- 24. Robinson, K.M., Cook, K.R. and Hanson, G.J. (2000) Velocity Field Measurements at an Overfall. Transactions of the ASAE, 43, 665-670. http://dx.doi.org/10.13031/2013.2748
- 25. Lin, C., Hwung, W.Y., Hsieh, S.C. and Chang, K.-A. (2007) Experimental Study on Mean Velocity Characteristics of Flow over Vertical Drop. Journal of Hydraulic Research, 45, 33-42.
http://dx.doi.org/10.1080/00221686.2007.9521741 - 26. Adrian, R.J. (1991) Particle-Imaging Techniques for Experimental Fluid Mechanics. Annual Review of Fluid Mechanics, 23, 261-304. http://dx.doi.org/10.1146/annurev.fl.23.010191.001401
- 27. Jähne, B., Klinke, J. and Waas, S. (1994) Imaging of Short Ocean Wind Waves: A Critical Theoretical Review. Journal of the Optical Society of America A: Optics and Image Science, 11, 2197-2209. http://dx.doi.org/10.1364/JOSAA.11.002197
- 28. Adrian, R.J. (2005) Twenty Years of Particle Image Velocimetry. Experiments in Fluids, 39, 159-169. http://dx.doi.org/10.1007/s00348-005-0991-7
- 29. Nicolas, K.R., Lindenmuth, W.T., Weller, C.S. and Anthony, D.G. (1997) Radar Imaging of Water Surface Flow Fields. Experiments in Fluids, 23, 14-19. http://dx.doi.org/10.1007/s003480050081
- 30. Craeye, C., Sobieski, P.W., Bliven, L.F. and Guissard, A. (1999) Ring-Waves Generated by Water Drops Impacting on the Water Surfaces at Rest. Journal of Oceanic Engineering, 24, 323-332.
http://dx.doi.org/10.1109/48.775294 - 31. Dabiri, D. and Gharib, M. (2000) Interaction of a Shear Layer with a Free Surface. 9th International Symposium on Flow Visualization, Paper No. 72.
- 32. Kouyi, G.L., Vazquez, J. and Poulet, J.B. (2003) 3D Free Surface Measurement and Numerical Modelling of Flows in Storm Overflows. Flow Measurement and Instrumentation, 14, 79-87.
http://dx.doi.org/10.1016/S0955-5986(03)00011-6 - 33. Douxchamps, D., Devriendt, D., Capart, H., Craeye, C., Macq, B. and Zech, Y. (2005) Stereoscopic and Velocimetric Reconstructions of the Free Surface Topography of Antidune Flows. Experiments in Fluids, 39, 535-553. http://dx.doi.org/10.1007/s00348-005-0983-7
- 34. Ni, W.J. and Capart, H. (2006) Groundwater Drainage and Recharge by Networks of Irregular Channels. Journal of Geophysical Research, 111, 1-33. http://dx.doi.org/10.1029/2005jf000410
- 35. Soares-Frazão, S., Le Grelle, N., Spinewine, B. and Zech, Y. (2007) Dam-Break Induced Morphological Changes in a Channel with Uniform Sediments: Measurements by a Laser-Sheet Imaging Technique. Journal of Hydraulic Research, 45, 87-95. http://dx.doi.org/10.1080/00221686.2007.9521835
- 36. Gardasson, S.M. and Yeh, H. (2007) Hysteresis in Shallow Water Sloshing. Journal of Engineering Mechanics, 133, 1093-1100. http://dx.doi.org/10.1061/(ASCE)0733-9399(2007)133:10(1093)
- 37. Stilwell, D. and Pilon, R.O. (1974) Directional Spectra of Surface Waves from Photographs. Journal of Geophysical Research, 79, 1277-1284. http://dx.doi.org/10.1029/JC079i009p01277
- 38. Lin, J., Kamotani, Y. and Ostrach, S. (1995) An Experimental Study of Free Surface Deformation in Oscillatory Themocapillary Flow. Acta Astronautica Journal, 35, 525-536.
http://dx.doi.org/10.1016/0094-5765(95)00004-J - 39. Mossa, M., Petrillo, A. and Chanson, H. (2003) Tailwater Level Effects on Flow Conditions at an Abrupt Drop. Journal of Hydraulic Research, 41, 39-51.
http://dx.doi.org/10.1080/00221680309499927 - 40. Lin, C., Juang, R.H. and Hsieh, S.C. (2003) Study on the Characteristics of Periodic Oscillation Flow over a Vertical Drop Energy-Dissipator. Journal of the Chinese Institute of Civil and Hydraulic Engineering, 15, 107-124. (In Chinese)
- 41. Jain, R., Kasturi, R. and Schunck, B.G. (1995) Machine Vision. McGraw-Hill, New York.
- 42. Capart, H., Young, D.L. and Zech, Y. (2002) Voronoï Imaging Methods for the Measurement of Granular Flows. Experiments in Fluids, 32, 121-135. http://dx.doi.org/10.1007/s003480200013
- 43. Cleveland, W.S. (1979) Robust Locally Weighted Regression and Smoothing Scatterplots. Journal of the American Statistical Association, 74, 829-836.
http://dx.doi.org/10.1080/01621459.1979.10481038 - 44. http://www.mathwork.com


















