Journal of Flow Control, Measurement & Visualization
Vol.02 No.04(2014), Article ID:49802,13 pages
10.4236/jfcmv.2014.24015
Generation of Arbitrary Pressure Pulsation of Wide Frequency Range for Flow Meter Testing in a Laminar Gas Pipeline
Mitsuhiro Nakao1, Tomonori Kato2, Takashi Oowaku3, Hirohisa Sakuma3, Toshiharu Kagawa4
1Department of Mechanical Engineering, Kagoshima University, Kagoshima, Japan
2Faculty of Engineering, Fukuoka Institute of Technology, Fukuoka, Japan
3Tokyo Gas Co., Ltd., Yokohama, Japan
4Precision and Intelligence Laboratory, Tokyo Institute of Technology, Yokohama, Japan
Email: nakao@mech.kagoshima-u.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 April 2014; revised 2 July 2014; accepted 25 July 2014
ABSTRACT
The present paper presents a device to test flow meters under an arbitrary pressure pulsation in a gas pipeline with a laminar flow containing frequency components up to 50 Hz, with the amplitude reaching hundreds of pascals. In order to reduce flow noise, the device has a strainer-like element connected to a pipeline under test and uses an open-loop control law based on the frequency response test. The control signal is calculated by adding the inputs to obtain each of the sinusoidal waves included in the original wave, which was decomposed by Fourier analysis. The validity of the developed method is demonstrated through the generation tests of superimposed pressure waves containing frequency components up to 50 Hz. Analysis of the relative uncertainty demonstrated the relative uncertainty to be less than 10% when the generated pressure is larger than 360 Pa.
Keywords:
Unsteady Flow, Flow Meter, Linear Wave, Superimposed Wave, Pneumatics

1. Introduction
Pulsations are a major source of error in flow measurements, as pointed by a number of researchers [1] - [3] . The generated error depends on both the type of the flow meter and the piping system used [1] - [3] . It is often the case that pipe flows are turbulent. In an actual pipeline having branches, however, there sometimes exist laminar flows provoked by unsteady flows in other branches. In a pulsating laminar flow, a periodically changing velocity distribution causes a relatively large error. In order to understand the performance of a flow meter under these circumstances, we need to examine a flow meter installed in a pipeline or duplicate the original pulsation in a laboratory experiment. The former approach is difficult because the true value of the flow rate is unknown. A laboratory-size instrument that can reproduce the original pulsation is needed for ease of testing.
A number of researchers have investigated unsteady flow rate testing devices, which can be categorized into flow rate control devices [4] - [6] and pressure control devices [7] . As an example of the former type, Durst et al. [4] proposed a mass flow controller consisting of a valve and a laminar element controlled by an open-loop control. This device is designed to work up to 125 Hz, and results up to 25 Hz are demonstrated. However, a disadvantage of the device is that the temperature of the gas discharged from the device changes during testing. Kawashima et al. [5] proposed an unsteady flow rate generator (UFG) using a chamber referred to as the isothermal chamber. The UFG has an advantage in that gas discharged from the UFG has an approximately constant temperature and a disadvantage in that the generation time is limited. Funaki et al. [6] modified the UFG to generate unsteady flows continuously. The modified UFG works well when flow rate to be examined is known such as in a frequency response test. However, it is difficult to evaluate the characteristics of a flow meter in a practical situation because the actual unsteady flow rate is rarely measureable. The pressure control device was proposed by Kato et al. [7] . The pressure control device controls the pressure pulsation at the inlet of a pipeline in order to generate an unsteady flow in order to evaluate the characteristics of a flow meter. An arbitrary pressure pulsation generating device (APPD) developed by Kato et al. [7] uses a feedback law based on the state equation of gas obtained by assuming that the pipeline under test can be treated as a lumped parameter system, and can reproduce pressure pulsations with small noise. This method can only reproduce a superimposed pressure wave including frequency components of up to 5 Hz. However, the actual frequency involved in the actual pulsating flow sometimes reaches tens of hertz. If the upper limit frequency of the APPD is improved, most actual pressure pulsations can be reproduced.
The objective of the present study is to develop an arbitrary pressure pulsation generating device, which can generate arbitrary pressure pulsations containing frequency components of up to 50 Hz, with an amplitude reaching hundreds of pascals. Such pressure pulsation occurs in real city gas pipelines, in which the line pressure is approximately 2.3 kPa, and a gas governor installed in the line has a natural frequency of 5 Hz or lower. It is usually satisfiable that the upper limit frequency is ten times of the natural frequency, but has not been achieved in the APPD. The present device has a configuration that is similar to that of an APPD, while using a different control law and concept. As the control law, an open-loop control law based on the frequency response characteristics is used to achieve a higher applicable frequency range. Instead of the large quasi-isothermal chamber used in a previous study [7] , a strainer-like element, such as a small quasi-isothermal chamber, is introduced in order to reduce the flow noise.
2. Experimental Apparatus
2.1. Generation Principle
Pressure pulsations arise from various sources, such as the switching operation of solenoid valves in gas pipelines for domestic use, and are distributed in space and time. The duplication of the original pressure pulsations is practically impossible because an actual gas pipeline with branches, which is longer by tens of meters, is not practical for reproduction in an experimental environment.
In the present study, a simulated version of the gas pipeline focused only around a flow meter is constructed in order to scale down the length direction. If a variable, such as pressure, on the boundary condition of the pipeline is adjusted to be more or less the same state, as compared to the corresponding location in the original pipeline, the simulated pipeline would have a pressure pulsation that is more or less correct, as compared with the original pipeline (See Figure 1). Although the boundary conditions at both ends of the simulated pipeline should be ideally controlled, these boundary conditions complicate the control law. The pipeline downstream of the flow meter can be constructed in an experimental environment, because this pipeline is only a few meters in length. Thus, the present paper describes results for the case in which only the upstream side of the pipeline is controlled. This method is valid when the controlled location is not on a node of a major frequency component included in the original wave.
Figure 1. Generation principle of pressure pulsation.
2.2. Experimental Configuration
The experimental configuration of the present device is shown in Figure 2. Air, supplied by an air compressor, passes through a buffer tank with a volume of 2.6 × 10−2 m3. Then, the air pressure is reduced to approximately 0.6 MPaG, and the air flows into quasi-isothermal chamber 1. The flow rate, flowing from quasi-isothermal chamber 1, into a strainer-like element via a servo valve (MPYE-5-1/8-LF-010B, FESTO Co., Ltd.), is changed by controlling the input voltage to the servo valve. As a strainer-like element, a quasi-isothermal chamber, crafted by tightly stuffing copper wool into an equal tee fitting of type 1, having an outer diameter of 110 mm, implemented in relation to JIS standard [8] , is used. A 4-m-long steel pipe, with an internal diameter of 28 mm is used as the piping system under test. Pressure P0 was measured using a semiconductor-type pressure sensor (XT190M-100A, Kulite Co., Ltd.), and pressures P1 and P2 were measured using piezoresistive differential pressure sensors (5 INCH-D-4V, All Sensors Co., Ltd.). All measured values were recorded using a computer, via an A/D convertor with a sampling frequency of 5 kHz. A D/A convertor gave the input voltage of the servo valve with the same frequency.
3. Frequency Response Test
First, the sonic conductance of the servo valve was obtained by experiment, using another experimental setup, as shown in Figure 3. Only the inlet port and one outlet port of the servo valve were used, and the other ports were closed with clinchers. The upstream pressure of the servo valve was set to approximately 0.6 MPaG in order to maintain a choked flow condition during the experiment. The volumetric flow rate passing through the servo valve was measured using a dry gas meter (DC-5A, SHINAGAWA, Co., Ltd.). During the test, the air temperature was 293 K, and the atmospheric pressure was 102 kPa. The volumetric flow rate passing through the servo valve in the chocked flow condition is expressed as follows [9] :
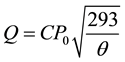 , (1)
, (1)
where C = sonic conductance, dm3/(s・MPa); P0 = upstream pressure, MPa (G); Q = volumetric flow rate, dm3/s (ANR); θ = air temperature, K. The sonic conductance of the servo valve was calculated by substituting the measured values into Equation (1). Figure 4 shows the obtained characteristics of the input voltage E and the sonic conductance C and an approximated curve calculated by the method of least squares for 0 ≤ E ≤ 4.5 V, where C is given in terms of E as follows:
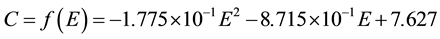 (2)
(2)
The quasi-sinusoidal flow rate is easily pumped into quasi-isothermal chamber 2 when the input voltage is given as follows:
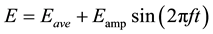 (3)
(3)
because the sonic conductance has strong linearity against the input voltage.
An example of the pressure response when the input voltage is set to E = 3.0 + 1.0sin (2π20t) is illustrated in Figure 5. Pressure P2 at the pipe outlet changed within 0.1 s of the start of the experiment and was approximately constant at 0 thereafter. Pressure P1 largely pulsated due to the stepwise change in the flow rate within 0.4 s of the start of the experiment. After 1.5 s, a quasi-sinusoidal pressure wave arose. This result implies that the inlet flow rate to isothermal chamber 2 and the pressure response of P2 have a linear relationship. In other words, when a sinusoidal flow rate with a frequency is input, this device will produce a
Figure 2. Pneumatic circuit of the developed equipment.
Figure 3. Experimental apparatus used in the sonic conductance test.
Figure 4. E-C characteristics of the servo valve.
Figure 5. Measured pressures with an applied voltage of 3.0 + 1.0sin (2π20t).
sinusoidal pressure wave including only the input frequency. In order to examine this supposition, frequency response tests were performed on the device. In particular, the pressure response of P1 was measured when the input voltage was given by Equation (3), in which Eave was 3.0 V, Eamp was 0.1, 0.5, and 1.0 V, and f was a frequency selected from among 1 Hz to 50 Hz frequency range with 1-Hz increments.
Each experiment was started at 0 s, and the data recording was started at 2 s and stopped at 4 s, for a total data recording time of 2 seconds. The data were then resolved into frequency components using the mixed radix fast Fourier transform algorithm, and the corresponding amplitudes and phases were obtained. Figure 6 represents a pressure response wave form of P1, in the case of Eamp = 0.1 and 1.0 V, and f = 1.0 Hz, and Figure 7 shows the corresponding frequency components. Figure 8 and Figure 9 show similar results for the case of Eamp = 0.1 V and f = 10 Hz, and Figure 10 and Figure 11 show the results for case of Eamp = 0.1 and 1.0 V and f = 30 Hz. The results for the case in which Eamp = 0.1 V in Figure 7, except for the 0-Hz component, the 1-Hz component of a frequency similar to the given frequency of pulsation dominates, whe-
Figure 6. Measured pressures with the applied voltage of (upper) 3.0 + 0.1sin (2πt) and (lower) 3.0 + 1.0sin (2πt).
Figure 7. Frequency components of the wave forms illustrated in Figure 6.
Figure 8. Measured pressures for an applied voltage of 3.0 + 0.1sin (2π10t).
Figure 9. Frequency components of the wave form illustrated in Figure 8.
Figure 10. Measured pressures for applied voltages of (upper) 3.0 + 0.1sin (2π30t) and (lower) 3.0 + 1.0sin (2π30t).
Figure 11. Frequency components of the wave forms illustrated in Figure 10.
reas the components around 10 Hz, corresponding to the Helmholtz resonance frequency, also have similar amplitude levels. On the other hand, a comparison of the results for Eamp = 0.1 V and 1.0 V reveals that the component at 1 Hz has a much larger amplitude for the case in which Eamp = 1.0 V, whereas the components around 10 Hz have approximately equal amplitudes in both cases. This is because the isothermal chamber acts as a porous material, which enhances small turbulent noise [10] while reducing large turbulent noise, and allows passage of the pressure wave [11] . The quasi-isothermal chamber is filled with very tightly packed copper wool [5] . Therefore, fluid flows through the narrow gaps in the wool, in the same manner as a porous material. The pressure form illustrated in Figure 8, is an almost pure sinusoidal waveform, because the given frequency is the natural frequency of the system. Actually, Figure 9 reveals that the frequency component equivalent to the natural frequency has an inordinate amplitude compared to the other components. Figure 10 and Figure 11 show similar results for a frequency of 30 Hz. In all of the cases presented above, the sinusoidal pressure responses with respect to sinusoidal inlet flow rates were obtained when the amplitude is relatively large.
The pressure response of a UFG was also investigated. The difference between a UFG and the present device is the existence of the strainer-like element. A UFG was constructed by removing the strainer-like element from the experimental apparatus shown in Figure 2. The pressure responses are summarized in Figure 12 for the case in which the input voltage is given by Equation (3), where Eave was 3.0 V, Eamp was selected so as to obtain a pressure amplitude of up to hundreds of pascals, and f was 1.0, 10, or 30 Hz. Comparison of Figure 6, Figure 8, Figure 10, and Figure 12 indicate that pressure wave forms generated with a UFG have a much larger turbulent noise compared to those generated by the present method. Furthermore, pressure wave forms generated with a UFG are non-linear with respect to the input flow rate. This result demonstrates the effectiveness of the strainer-like element.
4. Method of Generating an Arbitrary Pulsating Flow
4.1. Open-Loop Control Law
Among the most important facts presented herein is that the superposition of waves is valid, because the pressure wave addressed in this problem is a small-amplitude pressure wave that has a linear relation between the flow rate and the pressure pulsation. This means that if we can successfully generate individual pressure waves with a single frequency component included in an arbitrary pressure wave, we can reproduce an arbitrary pressure wave by superimposing the individual pressure waves.
Next, we present a definitive procedure for reproducing a target pressure pulsation. In practice, most periodic functions can be expanded in a Fourier series and can be described as a sum of trigonometric functions. The target pressure pulsation is generally expressed as follows:
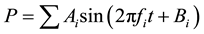 . (4)
. (4)
Here, we consider the following single frequency component:
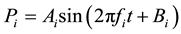 . (5)
. (5)
When the pressure of sine wave pulsation given in Equation (5) is reproduced, the inlet flow rate Q satisfies the following relation:

Next, the following relations are determined experimentally in advance:
Figure 12. Pressure pulsations generated by a UFG with respect to three sinusoidal inputs: (upper) 1.0 Hz, (middle) 10 Hz, and (bottom) 30 Hz.


Then, Equation (6) can be transformed as follows:

Considering the choked flow condition, the transformation of Equation (9) yields the following equation:

When we input the voltage corresponding to the sonic conductance given by Equation (10) to the servo valve, the pressure of sine wave pulsation given by Equation (5) is generated. If the target pressure pulsation has a number of frequency components, we can calculate the corresponding sonic conductance for each individual frequency by repeating the above-described process. The sonic conductance needed to reproduce the target pressure pulsation is then calculated as follows by taking the sum of the components based on the superposition of waves:

Finally, the input voltage is calculated as follows using the inverse relation between the input voltage and the sonic conductance of the servo valve:

4.2. Results of Pressure Pulsation Generation
The authors examined pulsating flow generation tests using the experimental equipment shown in Figure 2 in order to check the validity of the proposed method. Generation tests involving three sinusoidal inputs having frequencies of 1.0, 20, or 50 Hz were first conducted. Using the above-described procedure, the input voltages were obtained by open-loop control, where the reference voltage was calculated using a computer and a measured pressure of P0. Figure 13 shows the generation results and indicates that all of the generated
Figure 13. Pressure pulsations generated by the present method with respect to three sinusoidal inputs: (upper) 1.0 Hz, (middle) 20 Hz, and (bottom) 50 Hz.
pressures matched the reference values very well with no feedback compensation. Figure 14 shows the frequency components included in the reference signal. The wave forms shown in Figure 13 are decomposed by FFT. Comparison of these figures shows good agreement. We also examined a frequency response test of the APPD [7] against pressure pulsations with amplitude of 100 Pa. The result is summarized as a bode diagram shown in Figure 15. It is demonstrated that the APPD could not reproduce pressure waves with a frequency higher than 5 Hz since the phase delay is 135 degree at 5 Hz. Thus, the proposed open-loop control method can reproduce higher-frequency waves, as compared to the previous method, with a relatively large amplitude, which was difficult using the previous method.
A superimposed pressure wave including three frequency components of 5, 20, and 50 Hz was also generated. The results are shown in Figure 16. The generated super-imposed pressure pulsation shows excellent agreement with the reference. Figure 17 shows the frequency components included in the reference signal and the wave forms illustrated in Figure 16 decomposed by FFT. The frequency spectrum of the generated pulsation has a small error in comparison with the reference values, which may indicate that the pressure wave occurring in the present device is not a linear wave, but can be approximately treated as a linear wave.
Figure 14. Frequency components of the wave forms illustrated in Figure 13: (upper) 1.0 Hz, (middle) 20 Hz, and (bottom) 50 Hz.
Figure 15. Bode diagram of the APPD.
Figure 16. Generation results of the superimposed pressure wave.
Figure 17. Frequency components of the wave form illustrated in Figure 15.
There are three factors that cause the non-linearity: hysteresis of the servo valve, measurement noise, and induced noise downstream of the servo valve. The hysteresis generates causes non-linearity, and the noises enhance frequency components around the natural frequency, which is not in targeted signal. The validity of the present device as an approximative device for generating arbitrary pressure pulsations is thus confirmed.
5. Uncertainty Analysis
The present device generates pressure pulsations by means of open-loop control of the inlet flow rate into the test pipeline based on known frequency characteristics. Errors are generated in the determination of the frequency characteristics, the inlet flow rate generation, and the noise caused by the servo valve. The relative uncertainty analysis of the present device is discussed below [12] .
The errors related to the frequency characteristics are associated with the inlet flow rate and the wall pressure measurement. The uncertainty of the inlet flow rate depends on the temperature, the measurement of the upstream pressure, and the sonic conductance of the servo valve given by Equation (1). The uncertainty due to the change in the supply temperature is less than 1% when the supply temperature is larger than 250 K, because the temperature change in the isothermal chamber is only approximately 2.5 K [6] . The uncertainty due to the temperature measurement is 0.8 K. The uncertainty of the measurement of the upstream pressure is 0.8%. The uncertainty of the sonic conductance is estimated to be 1%. The standard uncertainty of the inlet flow rate is given by following formula from the propagation of uncertainty:

The uncertainty of the wall pressure measurement is 1.1%. Thus, the standard uncertainty of the frequency characteristics is given by following equation:

When the temperature is larger than 250 K, which is applicable in nearly all practical cases, the uncertainty of the inlet flow rate is less than 1.4% from Equation (13), and the uncertainty of the frequency characteristics is less than 1.8% from Equation (14).
The noise and nonlinearity generate errors. The uncertainty of this generated pressure is given by following equation:

where n = a number of the sampled data. All data illustrated in Figure 13 and Figure 15 was used to calculate Equation (15). The uncertainty depends on frequency as summarized in Table 1. The uncertainty is less than 35 Pa among all frequencies.
The total relative uncertainty of the present device is obtained by combining the above uncertainties as follows:

Equation (17) has validity when the temperature is larger than 250 K:

For example, the total relative uncertainty of the present device is less than 10% when the generated pressure is greater than 360 Pa. The greater the generated amplitude, the smaller the uncertainty of the present device.
6. Conclusion
In the present paper, we have proposed a device that can generate arbitrary pressure pulsations containing frequency components of up to 50 Hz with an amplitude reaching hundreds of pascals. A small quasi-isothermal chamber was introduced to the device as a strainer-like element in order to reduce turbulent noise. Frequency response tests demonstrated that pulsations with amplitudes of hundreds of pascals occurring in the device are linear waves, thus verifying the validity of the superposition principle, and the open-loop control law was developed based on the superposition principle. The control signal is calculated by adding up inputs to obtain each sinusoidal wave included in the original wave, which is decomposed by Fourier analysis. Reproduction tests of single sinusoidal pressure waves were carried out, and the results confirmed that the developed method can reproduce pressure pulsations of up to 50 Hz with small turbulent disturbances, which is not possible using existing devices. Furthermore, the proposed device also generated superimposed pressure waves containing three frequency components. Analysis of the relative uncertainty of the proposed device revealed a relative uncertainty of less than 10% for the case in which the amplitude of the pressure pulsation is greater than 360 Pa. The proposed device successfully improved the applicable frequency range of the pressure-control-type flow meter test device. Using the proposed device and pressure measurement in an actual pipeline, users can test flow meters under a wider range of pressure pulsations. The quasi-linear wave assumption loses validity in the turbulent flow case. A more complex control method will be needed to compensate the non-linearity to extend the present device to the turbulent flow case.
Table 1. Frequency dependency of the δP1,generated.
Acknowledgements
The authors would like to thank Mr. T. Hanada and Mr. T. Chifu, former students of Kagoshima University, for their assistance in conducting the experiment.
Cite this paper
MitsuhiroNakao,TomonoriKato,TakashiOowaku,HirohisaSakuma,ToshiharuKagawa, (2014) Generation of Arbitrary Pressure Pulsation of Wide Frequency Range for Flow Meter Testing in a Laminar Gas Pipeline. Journal of Flow Control, Measurement & Visualization,02,125-137. doi: 10.4236/jfcmv.2014.24015
References
- 1. Håkansson, E. and Delsing, J. (1994) Effects of Pulsating Flow on an Ultrasonic Gas Flowmeter. Flow Measurement and Instrumentation, 5, 93-101. http://dx.doi.org/10.1016/0955-5986(94)90042-6
- 2. Hanson, B.R. and Schwankl, L.J. (1998) Error Analysis of Flowmeter Measurements. Journal of Irrigation and Drainage Engineering, 124, 248-256. http://dx.doi.org/10.1061/(ASCE)0733-9437(1998)124:5(248)
- 3. Berrebi, J., Martinsson, P.E., Willatzen, M. and Delsing, J. (2004) Ultrasonic Flow Metering Errors Due to Pulsating Flow. Flow Measurement and Instrumentation, 15, 179-185. http://dx.doi.org/10.1016/j.flowmeasinst.2003.12.003
- 4. Durst, F., Heim, U., ünsal, B. and Kullik, G. (2003) Mass Flow Rate Control System for Time Dependent Laminar and Turbulent Flow Investigations.Measurement Science and Technology, 14, 893-902. http://dx.doi.org/10.1088/0957-0233/14/7/301
- 5. Kawashima, K. and Kagawa, T. (2003) Unsteady Flow Generator for Gases Using Isothermal Chamber. Measurement, 33, 333-340. http://dx.doi.org/10.1016/S0263-2241(03)00003-4
- 6. Funaki, T., Kawashima, K., Yamazaki, S. and Kagawa, T. (2007) Generator of Variable Gas Flows Using an Isothermal Chamber. Measurement Science and Technology, 18, 835-842. http://dx.doi.org/10.1088/0957-0233/18/3/036
- 7. Kato, T., Oowaku, T., Sakuma, H. and Kagawa, T. (2012) Introduction of a Newly Developed Arbitrary Pressure Pulsation Generating Device for Evaluating the Characteristics of Gas Flow Meters and Sensors. JFPS International Journal of Fluid Power System, 5, 16-21.
- 8. JIS B2301 (1994) Screwed Type Malleable Cast Iron Pipe Fitting.
- 9. JIS B8390 (2000) Pneumatic Fluid Power Components Using Compressible Fluids Determination of Flow Rate Characteristics.
- 10. Takatsu, Y. and Masuoka, T. (2002) Production and Dissipation of Turbulence in Porous Media. Transactions of JSME series B, 68, 2601-2605.
- 11. Sueki, T., Takaishi, T., Ikeda, M. and Arai, N. (2010) Application of Porous Material to Reduce Aerodynamic Sound from Bluff Bodies. Fluid Dynamics Research, 42, 015004. http://dx.doi.org/10.1088/0169-5983/42/1/015004
- 12. ISO (1995) Guide to the Expression of Uncertainty in Measurement.
Nomenclature



















