Open Journal of Earthquake Research
Vol.04 No.03(2015), Article ID:58297,8 pages
10.4236/ojer.2015.43008
An Integrated Study of ULF Magnetic Field Variations in Association with the 2008 Sichuan Earthquake, on the Basis of Statistical and Critical Analyses
Masashi Hayakawa1,2,3, Alexander Schekotov2,4, Stelios M. Potirakis5, Konstantinos Eftaxias6, Qi Li7, Tomokazu Asano8
1Hayakawa Institute of Seismo Electromagnetics, Co. Ltd., University of Electro-Communications (UEC) Incubation Center, Tokyo, Japan
2Advanced Wireless & Communications Research Center, UEC, Tokyo, Japan
3Earthquake Analysis Laboratory, Information Systems Inc., Tokyo, Japan
4Institute of Physics of the Earth, Russian Academy of Sciences, Moscow, Russia
5Department of Electronics Engineering, Piraeus University of Applied Sciences (TEI of Piraeus), Athens, Greece
6Department of Physics, University of Athens, Athens, Greece
7Institute of Geophysics, China Earthquake Administration, Beijing, China
8Fuji Security Systems Co., Ltd., Tokyo, Japan
Email: hayakawa@hi-seismo-em.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 June 2015; accepted 21 July 2015; published 24 July 2015
ABSTRACT
The ultra-low frequency (ULF) magnetic field data at a station very close to the 2008 Sichuan earthquake (EQ) (on 12 May, 2008; M = 8.0) are extensively studied on the basis of combined statistical and natural time analyses. Two effects in ULF are treated: one is the well-known ULF radiation from the lithosphere, and the other is the non-conventional depression of ULF horizontal magnetic field. The simple statistical analysis has yielded: 1) no clear evidence of the presence of precursory ULF radiation, and 2) a significant effect of depression of ULF horizontal field a few days before the EQ (as a signature of ionospheric perturbations). The recently introduced natural time analysis has also been performed in order to study the critical features of the lithosphere and essentially new information has been brought about. The parameter “polarization”, as the ratio of vertical to horizontal components, showed critical features in the time period of 17 - 27 April, about one month to two weeks before the EQ as a signature of lithospheric radiation. Then, the natural time analysis has reconfirmed the presence of ionospheric perturbations a few days before the EQ, together with an additional time window found on 19 - 23 April, about one month before the EQ, exhibiting critical features in the ULF depression.
Keywords:
2008 Sichuan EQ, ULF Magnetic Field Variations, Statistical Analysis, Critical Analysis, EQ Precursor

1. Introduction
There has been a lot of evidence accumulated during the last few decades on the presence of electromagnetic phenomena associated with or prior to earthquakes (EQs), and such seismo-electromagnetic effects are considered to be promising for short-term EQ prediction (e.g., [1] -[3] ). It is found that there are two different kinds of electromagnetic precursors: one is direct radiation in different frequency bands from the EQ hypocenter (or epicenter), and the other is seismo-atmospheric and -ionospheric perturbations (i.e., pre-EQ perturbations of the atmosphere and ionosphere) (e.g., [4] - [7] ).
Some of the electromagnetic precursors are found to be statistically correlated with EQs. Such an example is the ionospheric perturbation in the lower ionosphere by means of subionospheric VLF/LF propagation anomalies [8] and also in the upper ionosphere on the basis of ionosonde observations etc. [9] . However, statistical studies for any other electromagnetic precursors are still highly required [10] .
Besides the above statistical studies, case studies for any particular EQs are still of great importance in studying the whole view for seismo-electromagnetic effects. An example of these case studies is the 1995 Kobe EQ [11] , in which the results from different observational items were collected and compared. In this paper, we take the 2008 Sichuan EQ as an example, and we make use of the ULF magnetic field data for this EQ. As already described in Li et al. [12] , there have been several papers published on electromagnetic precursors to this EQ, but the main phenomena were the ionospheric perturbations observed from the ground- and satellite-based measurements. As compared with various electromagnetic and plasma anomalies in association with this EQ, the analysis of ground-based ULF magnetic field changes is very rare (details are given in [12] ), which is the topic of this paper.
When using the ULF magnetic field data, we can study two different aspects of ULF effects. The first is the well-known lithospheric ULF radiation from the EQ hypocenter. Lithospheric ULF radiation has been observed prior to large EQs, such as Spitak EQ [13] [14] , Loma Prieta EQ [15] , and Guam EQ [16] . A new non-conven- tional effect in ULF was discovered by Schekotov et al. [17] , which is vice versa of the first effect. That is the depression of ULF horizontal magnetic field component before an EQ, which is explained in terms of the enhanced absorption of magnetospheric ULF waves through the perturbed lower ionosphere [18] [19] . These two effects will be discussed together in this paper.
2. Description of the Sichuan EQ and ULF Data
The 2008 Sichuan EQ happened on 14:28:01 Chinese Standard Time (or 06:28:01 UT) on 12 May, 2008 in the Sichuan province. Its magnitude was M = 8.0 and its depth was 19 km. The epicenter of this EQ is located at the geographic coordinates (31˚01'05"N, 103˚36'05"E), which is shown in Figure 1 as the center of the largest circle. This EQ is also known as Wenchuan EQ after its epicentral location in the Wenchuan county, Sichuan, but we call it “Sichuan EQ” in this paper. The EQ epicenter was 80 km west-north of Chengdu, the provincial capital. Strong aftershocks, some exceeding the magnitude 6, continued to hit the area even months after the main shock as shown in Figure 1 by several circles.
Figure 1 illustrates the locations of two stations of observing ULF magnetic fields, Chengdu (abbreviated as CDP) and Xichang (XIC) as black diamonds. The magnetometer at those stations is of the fluxgate type, and its sampling frequency is 1 Hz.
3. Statistical Analysis
The observation of ULF magnetic field variations at CDP started in the beginning of January 2008, but the first
Figure 1. Relative location of the EQ epicenters and two ULF observation stations (Chengdu (CDP)) and Xichang (XIC)). The epicenter of the 2008 Sichuan EQ is the center of the largest circle. Other colorful circles are its aftershocks. The magnitude of the circle is proportional to the magnitude, while the color reflects the EQ depth.
month was omitted due to a large level of industrial interferences, so that we have used a 5-month period from 1 February to 30 June, 2008 including the EQ date. The nighttime interval defined by LT = 22 h to 02 h (UT = 1 h - 5 h) is utilized as the time when the noise level is low and maximum of expected effect of ULF depression is usually observed. The minimal value of the magnetic field power averaged over a few 30-min overlapped intervals is used, yielding one datum per day. This procedure was described in [12] . The frequency band is chosen as 0.005 - 0.01 Hz (5 - 10 mHz) after an extensive analysis of the possibility to detect ULF depression. This objective was less successfully achieved at higher or lower frequencies. Figure 2 is the analysis results at the station of CDP. Top panel illustrates the temporal evolutions of seismic activity expressed by Kls as a function of EQ magnitude and epicentral distance [1] and geomagnetic activity (Dst). The second and third panels illustrate the temporal evolutions of horizontal magnetic field (H) intensity (in power) (Fh) and vertical magnetic field (Z) intensity (in power) (Fz). The fourth panel refers to the temporal evolution of the ratio of vertical to horizontal component (Pz/h) [16] called polarization. The fifth panel refers to the inverse of horizontal component (Dh) in order to try to find the depression of ULF horizontal component (second ULF effect), and the bottom panel refers to the temporal evolution of δDep (by using the above Dh) as the most promising parameter to find the ULF horizontal field depression. The definition of δDep is given in [18] , but we mention here that δDep is the ratio of daily depression (Dh) relative to its mean value for the previous 30 days to that mean value.
By using those ULF data, Li et al. [12] have performed the conventional statistical analysis and come to the following conclusion.
1) There is no clear evidence on the presence of lithospheric ULF radiation.
2) A significant effect seems to be detected in the ULF horizontal magnetic field depression a few days before the main shock on 12 May (as seen from the significant peak in δDep just before the main shock in the bottom panel of Figure 2).
The conventional statistical analysis can be defined as a method to identify any extreme values, i.e., local maxima or local minima. In other words, we try to find the value exceeding the 2σ (σ: standard deviation) criterion or the value below the −2σ level. When the value (either any one of Fh, Fz, Dh or so) is found to lie within the range of −2σ - +2σ, we cannot say anything about the abnormality of the value. In all previous ULF works [10] [13] -[16] [20] , except ours [17] -[19] , the researchers have dealt with this well-known lithospheric ULF radiation, i.e., an increase in the power of ULF magnetic field components (Fh, Fz). Further, the quantity, called polarization [16] was suggested to distinguish seismogenic ULF from the space effect (geomagnetic variation, ULF geomagnetic pulsations). Recently, Currie and Waters [21] have concluded based on the one- year data analysis that this parameter of polarization is very insensitive to geomagnetic activity, so that they have suggested this parameter to be well suited to identifying the seismogenic effect.
Figure 2. Top panel illustrates the temporal evolution of seismic activity expressed by Kls and geomagnetic activity (Dst) (in nT) during our analysis period from 1 February to the end of June, 2008. The largest Kls indicates the 2008 Sichuan EQ on 12 May. The second and third panels illustrate the temporal evolutions of Fh (horizontal magnetic field) and Fz (vertical magnetic field), where the power is averaged over nighttime on each day. The fourth panel refers to the parameter, polarization, Pz/h. The fifth and sixth panels refer to the depression of horizontal magnetic field, Dh and δDep, respectively.
However, we have to emphasize that there exists another non-conventional effect, that is, the depression of horizontal magnetic field before an EQ as a signature of seismo-ionospheric perturbations [17] [18] . This effect is unfortunately not well known to the scientific community yet. The finding of this non-conventional effect makes it very complicated when we analyze the ULF magnetic field variations.
So, in the next section we use one of the critical analysis methods: natural time (NT) analysis to analyze the critical features in the lithosphere and to find definite evidence of precursors, even though the statistical analysis could not yield any definite conclusion on the presence of lithospheric ULF radiation. Additionally, we want to re-confirm the presence of ULF magnetic field depression as found in [12] .
4. Critical Natural Time (NT) Analysis
4.1. Parameters of ULF Magnetic Fields to Be Analyzed
The concept of NT analysis is suitable for time series data of point processes, including seismicity and DC geoelectric potential. On the other hand, ULF variations are not a point process, but they are continuous in nature, so that we have to think of what kind of ULF parameters should be used for the NT analysis.
As the first step in order to convert the continuous ULF data to discrete data, we have used the averaged intensity over the nighttime. The following ULF parameters (average value during the night on a particular day) as already described above, are subjected to the NT analysis (e.g., [22] for the 2011 Tohoku EQ).
1) Horizontal magnetic field component, H component (power): 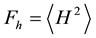
2) Vertical magnetic field component, Z component (power): 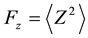
3) Polarization: ratio of vertical to horizontal components: Pz/h
4) Depression of horizontal magnetic field component: 
5) δDep: ratio of daily depression (Dh) relative to its mean value for previous 30 days to the mean
The first three parameters (Fh, Fz, and Pz/h) are considered to be indicators of ULF emission from the lithosphere. The fourth parameter, Dh, is the inverse of the horizontal magnetic field component so as to pay extensive attention to the changes in minimum values for investigating the depression of ULF waves (of magnetospheric origin) observed on the ground as the ionospheric signature. The last parameter is δDep, which is defined as above.
4.2. NT Analysis Method
The transformation of a time-series of “events” from the conventional time domain to the NT domain is performed by ignoring the time interval between events and retaining only its normalized order of occurrence [23] . So the kth event corresponds to a NT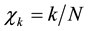 , where N is the total number of successive events. The “energy”
, where N is the total number of successive events. The “energy” 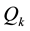 of each event is also retained. Then the time series (
of each event is also retained. Then the time series (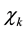 ,
,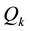 ) is studied. A system is considered to
) is studied. A system is considered to
approach criticality when the parameter 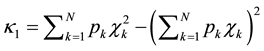 (
(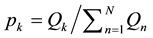 is the energy of kth
is the energy of kth
event normalized by the total energy) converges to 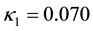 and at the same time both the entropy in NT,
and at the same time both the entropy in NT,
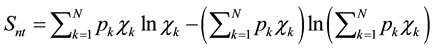 and the entropy under time reversal,
and the entropy under time reversal,  , satisfy the con-
, satisfy the con-
dition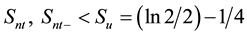 , where
, where 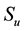 stands for the entropy of a “uniform” distribution in NT [23] [24] .
stands for the entropy of a “uniform” distribution in NT [23] [24] .
The criticality is considered truly achieved when the following three conditions are also satisfied: i) the “average” distance 








4.3. Results of NT Analysis of ULF Parameters
We present here the results only at CDP because the period of useful data at another remote station of XIC in Figure 1 is very limited and the recording there is characterized by bad data. First we summarize the NT analysis results concerning lithospheric ULF radiation.
1) No criticality was observed for Fz.
2) Fh showed criticality characteristics on 17 April, almost one month before the EQ, but only for one threshold value.
3) Pz/h indicates that criticality conditions are met for a large number of different threshold values within the time period of 17 - 27 April. This parameter seems to provide the clearer results as the NT analysis variable. Sample figures presenting the corresponding NT analysis results are given in Figures 3(a)-(d).
Next we move on to the results for the non-conventional ULF effect; ULF depression effect.
1) Dh indicates that criticality conditions are reached for a number of different threshold values within the time period of 19 - 23 April. Sample figures presenting the corresponding NT analysis results are given in Figure 4(a) and Figure 4(b).
2) δDep showed criticality for some specific thresholds: (a) marginally on 6 May (only for the threshold 0.55, see Figure 4(c)) and Figure 4(b) on 8 May (for the threshold 0.20, see Figure 4(d)).
Some explanations are required for these Figure 3 and Figure 4. We consider each daily value which is above a
Figure 3. Natural time (NT) analysis result for Pz/h during our analysis period: (a)-(d) Temporal evolutions of the four natural time analysis parameters



Figure 4. The same as in Figure 3, but (a) and (b) for Dh and the threshold values 1000 and 2500 (in au), respectively, as well (c) and (d) for δDep and the threshold values 0.55 and 0.20 (in au), respectively. The explanation of x-axis is the same as in Figure 3.
certain threshold as an event. So in our case, the energy of kth event Qk is considered to be equal to each one of the above quantities (Fh, Fz etc.). All the parameters (



5. Summary and Discussion
We have used the ULF data observed at CDP very close to the EQ epicenter (with epicentral distance of 80 km), and nighttime data are utilized. The frequency band was chosen to be 0.05 - 0.01 Hz (5 - 10 mHz) after extensive studies of spectral analyses in different frequency bands.
Based on a combined study of the results by both the conventional statistical and critical NT analyses, we summarize first the findings for lithospheric ULF radiation.
1) The conventional statistical analysis has yielded no evident signature of lithospheric radiation.
2) But, the NT analysis has indicated that the parameter, polarization Pz/h showed critical features in the time period of 17 - 27 April, about one month to two weeks before the EQ.
In the NT analysis, the nature of being self-similar is the most important factor for the critical features. The analysis showed that time of criticality for Pz/h does not change significantly by varying the threshold, so that the result for Pz/h is likely to be acceptable. The critical feature is considered to have taken place in the lithosphere very close to the observation station (or the EQ epicenter). Lithospheric ULF radiation is known to be detected within a rather small area with radius on the order of 100 km [20] , so that this area was at a critical stage about one month to two weeks before the EQ. Our finding that the criticality at CDP was not reflected in Fz, but in Fh and Pz/h, may be explained by the relative position of the current source and observatory. Dynamic processes in association with the pre-EQ microfracture can lead to the generation of current systems, even though the mechanism of electrification in the source region is not well understood [1] [25] . So we can infer that the source current which was, at least, responsible for the seismogenic ULF radiation observed at CDP might have been generated about 2 - 4 weeks before the 2008 Sichuan EQ in an area close to the station, CDP. The lead time in this paper seems to be consistent with that of former works [20] . As the last point, we comment on a comparison of amplitude with previous huge EQs like Spitak, Loma Prieta, Guam etc. When thinking about the magnitude of this EQ (M = 8), we would have expected higher-amplitude ULF radiation, which is detectable even by the simple statistical analysis, but this was not the case. Only the NT analysis has succeeded in detecting ULF radiation, and this means that the ULF radiation was not so strong in amplitude for the 2008 Sichuan EQ, which is worth thinking of this discrepancy in the future.
Then, we come to the conclusion of the non-conventional ULF depression effect as a signature of seismo-io- nospheric perturbations.
1) The conventional statistical analysis has yielded that δDep showed a clear peak a few days before the EQ.
2) The NT analysis has reconfirmed the presence of precursors in δDep a few days before the EQ, though not exactly on the same day as in the statistical analysis.
3) The NT analysis has indicated additional critical features in the time period of 19 - 23 April, about one month before the EQ.
Both the statistical and NT analyses have confirmed the presence of precursors in δDep a few days before the EQ, so that these results are indicative of high probability of δDep (ULF depression) as a precursor to the EQ. Because the ULF depression may be satisfactorily interpreted in terms of an enhanced absorption of downgoing Alfven waves through the perturbed lower ionosphere, suggesting the generation of seismo-lower ionospheric perturbations [18] [19] . Though some other mechanisms including the nonlinear process have been proposed (e.g., [1] [26] ), all are based on the perturbations in the lower ionosphere. We have an additional time period exhibiting critical features in δDep about one month before the EQ. The area of ionospheric perturbation as sensed by the ULF horizontal magnetic field depression is known to be much wider than that sensed by the above lithospheric radiation [18] [19] . So, it seems that the pre-EQ criticality has occurred in a wider area of lithosphere in two time periods before the EQ; one is a few days before the EQ, and the other is about one month before the EQ. The lead time of the lower ionospheric perturbation is found to be on the order of one week [8] , so that the former lead time obtained in this paper is very plausible.
A difference in lead time of critical dates for lithospheric ULF radiation and for ionospheric perturbations as deduced from Dh and δDep (ULF depression), might be simply due to the difference in the location of lithosphere sensed by both methods.
One more thing we have to add here is the consideration on geomagnetic activity, which might have some effects on ULF. As already described in [12] , the geomagnetic activity during the period of our analysis was rather calm, so its influence can be neglected.
Finally, we have to emphasize the following points again. First, we have to pay attention to both effects in ULF, i.e., not only the well-known lithospheric radiation, but also a new phenomenon of depression of ULF horizontal magnetic fields as a signature of seismo-ionospheric perturbations. As the second point, we advise the readers to carry out an integrated study for any seismogenic phenomenon by using both the simple statistical and critical analyses, because there is a definite limitation in studying the physics of a seismogenic phenomenon only with the use of the conventional statistical analysis.
Acknowledgements
The authors are grateful to Advanced National Seismic System (ANSS) for providing us with the data of seismicity. Then, we thank the staffs of the YS station of the China Earthquake Networks Center in the Yunnan province for their assistance in ULF observation.
Cite this paper
MasashiHayakawa,AlexanderSchekotov,11,11,Stelios M.Potirakis,KonstantinosEftaxias,QiLi,TomokazuAsano, (2015) An Integrated Study of ULF Magnetic Field Variations in Association with the 2008 Sichuan Earthquake, on the Basis of Statistical and Critical Analyses. Open Journal of Earthquake Research,04,85-93. doi: 10.4236/ojer.2015.43008
References
- 1. Molchanov, O.A. and Hayakawa, M. (2008) Seismo-Electromagnetics and Related Phenomena: History and Latest Results. TERRAPUB, Tokyo, 189 p.
- 2. Hayakawa, M. (2009) Electromagnetic Phenomena Associated with Earthquakes. Transworld Research Network, Trivandrum, 279 p.
- 3. Hayakawa, M. (2013) Earthquake Prediction Studies: Seismo Electromagnetics. TERRAPUB, Tokyo, 168 p.
- 4. Uyeda, S., Kamogawa, M. and Nagao, T. (2009) Short-Term Earthquake Prediction: Current Status of Seismo-Electromagnetics. Tectonophysics, 470, 205-213. http://dx.doi.org/10.1016/j.tecto.2008.07.019
- 5. Hayakawa, M. and Hobara, Y. (2010) Current Status of Seismo-Electromagnetics for Short-Term Earthquake Prediction. Geomatics, Natural Hazards and Risk, 1, 115-155. http://dx.doi.org/10.1080/19475705.2010.486933
- 6. Eftaxias, K. and Potirakis, S.M. (2013) Current Challenges for Pre-Earthquake Electromagnetic Emissions: Shedding Light from Micro-Scale Plastic Flow, Granular Packings, Phase Transitions and Self-Affinity Notion of Fracture Process. Nonliner Processes in Geophysics, 20, 771-792. http://dx.doi.org/10.5194/npg-20-771-2013
- 7. Eftaxias, K., Potirakis, S.M. and Chelidze, T. (2013) On the Puzzling Feature of the Silence of Precursory Electromagnetic Emissions. Natural Hazards and Earth System Science, 13, 2381-2397. http://dx.doi.org/10.5194/nhess-13-2381-2013
- 8. Hayakawa, M., Kasahara, Y., Nakamura, T., Muto, F., Horie, T., Maekawa, S., Hobara, Y., Rozhnoi, A., Solovieva, M. and Molchanov, O.A. (2010) A Statistical Study on the Correlation between Lower Ionospheric Perturbations as Seen by Subionospheric VLF/LF Propagation and Earthquakes. Journal of Geophysical Research, 115, A09305. http://dx.doi.org/10.1029/2009ja015143
- 9. Liu, J.Y. (2009) Earthquake Precursors Observed in the Ionospheric F-Region. In: Hayakawa, M., Ed., Electromagnetic Phenomena Associated with Earthquakes, Transworld Research Network, Trivandrum, 187-204.
- 10. Hattori, K. (2013) ULF Geomagnetic Changes Associated with Major Earthquakes. In: Hayakawa, M., Ed., Earthquake Prediction Studies: Seismo Electromagnetics, TERRAPUB, Tokyo, 129-152.
- 11. Nagao, T., Enomoto, Y., Fujinawa, Y., Hata, M., Hayakawa, M., Huang, Q., Izutsu, J., Kushida, Y., Maeda, K., Oike, K., Uyeda, S. and Yoshino, T. (2002) Electromagnetic Anomalies Associated with 1995 Kobe Earthquake. Journal of Geodynamics, 33, 477-487. http://dx.doi.org/10.1016/s0264-3707(02)00004-2
- 12. Li, Q., Schekotov, A., Asano, T. and Hayakawa, M. (2015) On the Anomalies in ULF Magnetic Field Variations Prior to the 2008 Sichuan Earthquake. Open Journal of Earthquake Research, 4, 55-64. http://dx.doi.org/10.4236/ojer.2015.42005
- 13. Kopytenko, Y.A., Matiashvily, T.G., Voronov, P.M., Kopytenko, E.A. and Molchanov, O.A. (1990) Discovering of Ultra-Low-Frequency Emissions Connected with Spitak Earthquake and Its Aftershock Activity on Data of Geomagnetic Pulsations Observations at Dusheti and Vardzija. IZMIRAN Preprint N3, 888, 27 p.
- 14. Molchanov, O.A., Kopytenko, Y.A., Voronov, P.M., Kopytenko, E.A., Matiashvili, T.G., Fraser-Smith, A.C. and Bernardy, A. (1992) Results of ULF Magnetic Field Measurements near the Epicenters of the Spitak (Ms = 6.9) and the Loma-Prieta (Ms = 7.1) Earthquakes: Comparative Analysis. Geophysical Research Letters, 19, 1495-1498. http://dx.doi.org/10.1029/92GL01152
- 15. Fraser-Smith, A.C., Bernardy, A., McGill, P.R., Ladd, M.E., Helliwell, R.A. and Villard Jr., O.G. (1990) Low-Frequency Magnetic Field Measurements near the Epicenter of the Ms 7.1 Loma-Prieta Earthquake. Geophysical Research Letters, 17, 1465-1468. http://dx.doi.org/10.1029/GL017i009p01465
- 16. Hayakawa, M., Kawate, R., Molchanov, O.A. and Yumoto, K. (1996) Results of Ultra-Low-Frequency Magnetic Field Measurements during the Guam Earthquake of 8 August 1993. Geophysical Research Letters, 23, 241-244. http://dx.doi.org/10.1029/95GL02863
- 17. Schekotov, A., Molchanov, O.A., Hattori, K., Fedorov, E., Gladyshev, V.A., Belyaev, G.G., Chebrov, V., Sinitsin, V., Gordeev, E. and Hayakawa, M. (2006) Seismo-Ionospheric Depression of the ULF Geomagnetic Fluctuations at Kamchatka and Japan. Physics and Chemistry of the Earth, 31, 313-318. http://dx.doi.org/10.1016/j.pce.2006.02.043
- 18. Schekotov, A., Fedorov, E., Molchanov, O.A. and Hayakawa, M. (2013) Low Frequency Electromagnetic Precursors as a Prospect for Earthquake Prediction. In: Hayakawa, M., Ed., Earthquake Prediction Studies: Seismo Electromagnetics, TERRAPUB, Tokyo, 81-99.
- 19. Hayakawa, M., Rozhnoi, A., Solovieva, M., Hobara, Y., Ohta, K., Schekotov, A. and Fedorov, E. (2013) The Lower Ionospheric Perturbation as a Precursor to the 11 March 2011 Japan Earthquake. Geomatics, Natural Hazards and Risk, 4, 275-287. http://dx.doi.org/10.1080/19475705.2012.751938
- 20. Hayakawa, M., Hattori, K. and Ohta, K. (2007) Monitoring of ULF (Ultra-Low-Frequency) Geomagnetic Variations Associated with Earthquakes. Sensors, 7, 1108-1122. http://dx.doi.org/10.3390/s7071108
- 21. Currie, J.L. and Waters, C.L. (2014) On the Use of Geomagnetic Indices and ULF Waves for Earthquake Precursor Signatures. Journal of Geophysical Research: Space Physics, 119, 992-1003. http://dx.doi.org/10.1002/2013ja019530
- 22. Hayakawa, M., Schekotov, A., Potirakis, S. and Eftaxias, K. (2015) Criticality Features in ULF Magnetic Fields Prior to the 2011 Tohoku Earthquake. Proceedings of the Japan Academy: Series B, 91, 25-30. http://dx.doi.org/10.2183/pjab.91.25
- 23. Varotsos, P.A. (2005) The Physics of Seismic Electric Signals. TERRAPUB, Tokyo, 338 p.
- 24. Varotsos, P.A., Sarlis, N.V., Skordas, E.S., Tanaka, H.K. and Lazaridou, M.S. (2006) Entropy of Seismic Electric Signals: Analysis in the Natural Time under Time Reversal. Physical Review E, 73, Article ID: 031114. http://dx.doi.org/10.1103/PhysRevE.73.031114
- 25. Surkov, V. and Hayakawa, M. (2014) Ultra and Extremely Low Frequency Electromagnetic Fields. Springer, Tokyo, 486 p. http://dx.doi.org/10.1007/978-4-431-54367-1
- 26. Sorokin, V. and Hayakawa, M. (2014) Plasma and Electromagnetic Effects Caused by the Seismic-Related Disturbances of Electric Current in the Global Circuit. Modern Applied Science, 8, 61-83. http://dx.doi.org/10.5539/mas.v8n4p61





