Open Journal of Earthquake Research
Vol.2 No.3(2013), Article ID:35776,8 pages DOI:10.4236/ojer.2013.23005
Reliability Index of Tall Buildings in Earthquake Zones
Department of Civil and Architectural Engineering, Qatar University, Doha, Qatar
Email: m.alansari@qu.edu.qa
Copyright © 2013 Mohammed S. Al-Ansari. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 3, 2013; revised July 5, 2013; accepted July 29, 2013
Keywords: Reliability Index; Earthquake; Interaction Chart
ABSTRACT
The paper develops a reliability index approach to assess the reliability of tall buildings subjected to earthquake loading. The reliability index β model measures the level of reliability of tall buildings in earthquake zones based on their response to earthquake loading and according to their design code. The reliability index model is flexible and can be used for: 1) all types of concrete and steel buildings and 2) all local and international codes of design. Each design code has its unique reliability index β as a magnitude and the interaction chart corresponding to it. The interaction chart is a very useful tool in determining the building drift for the desired level of reliability during the preliminary design of the building members. The assessments obtained using the reliability index approach of simulated, tested, and actual buildings in earthquake zones were acceptable as indicators of the buildings reliability.
1. Introduction
The lateral displacement or drift of structural systems during an earthquake has an important impact on their potential failure. The probability of failure of structures is therefore reduced by limiting their lateral displacements or drifts. The reliability index β, which is typically used to measure the probability of failure of structural systems, allows structures to reach the desired reliability level through the assessment of the likelihood that their earthquake responses exceed predefined building drift values (roof displacement). The reliability index approach made it possible for the reduction of the probability of failure of building structures [1-6].
Drift limitations are currently imposed by seismic design codes, such as Uniform building Code (UBC) and International Building Code (IBC), in order to design safe buildings [7,8]. The acceptable range for the drift index of conventional structures lies between the values of 0.002 and 0.005 (that is approximately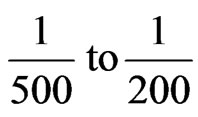 ).
).
Excessive lateral displacements or drifts can cause failure in both structural and non-structural elements. Therefore, drifts at the final structural design stages must satisfy the desired reliability level and must not exceed the specified index limits [9-13]. While extensive research has been done in this important topic, no or limited studies addressed the use of reliability index to assess the building reliability in earthquake zones based on their lateral displacement and drift.
This paper develops a probabilistic model using the reliability index approach to assess the reliability of concrete and steel buildings subjected to earthquake loading in different zones and soil profiles based on their responses to earthquake loading, Table 1. The non-linear dynamic response of buildings was obtained using three simulated models of buildings, square, circular, and tube with different heights, Figures 1-4.
Other real buildings such as the full scale seven story reinforced concrete building that was tested statically and dynamically in Japan conducted under the US-Japan Cooperative Earthquake Engineering Research Program on the seismic performance of the building structure Figure 5 [14].
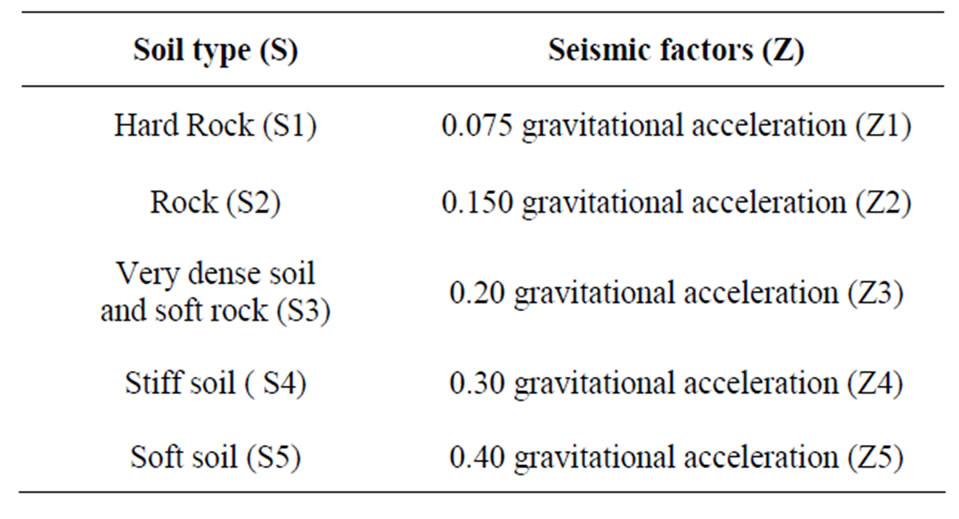
Table 1. Soil profile and seismic factors.



Figure 1. 3D Structural Building Models.
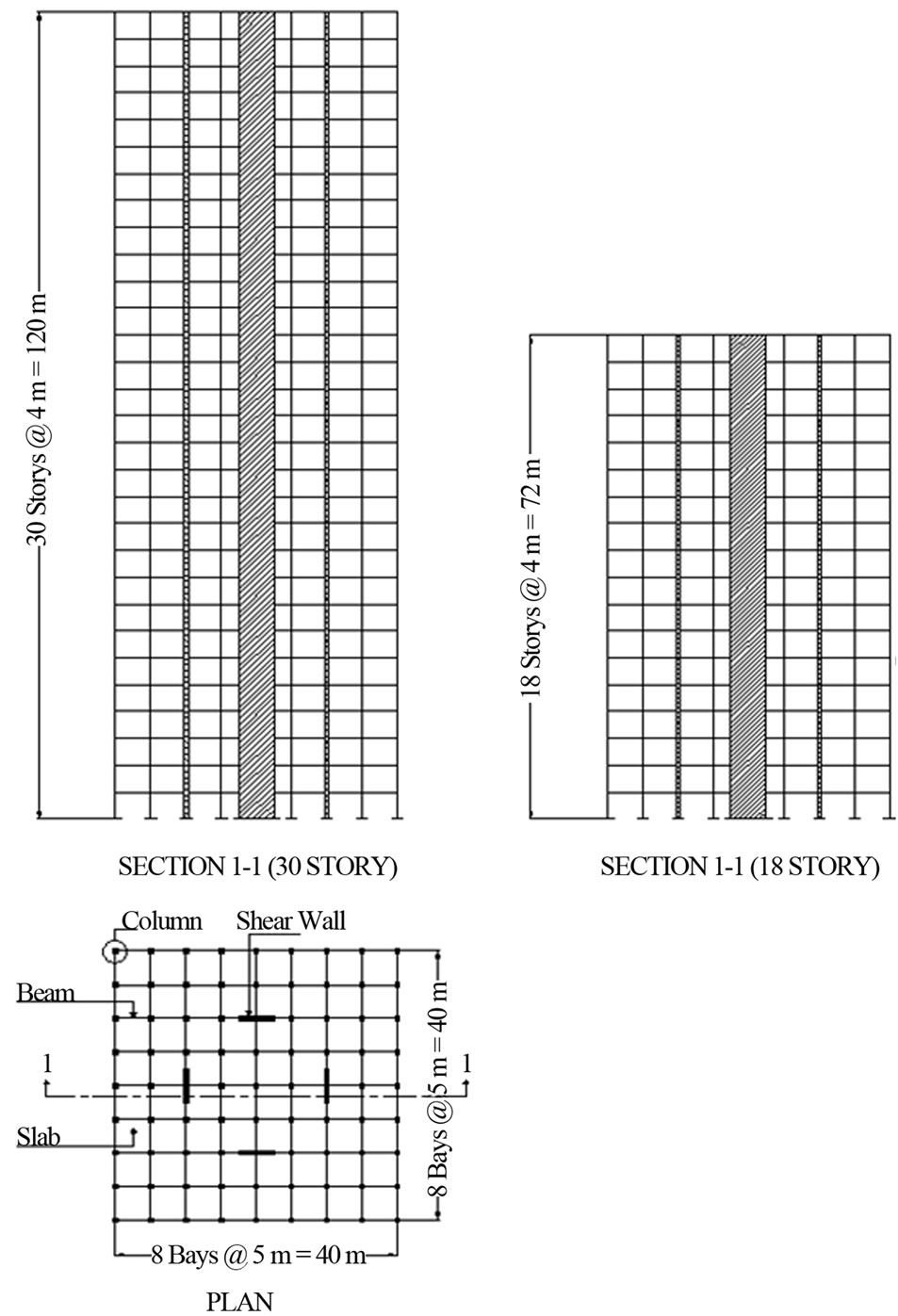
Figure 2. Square Building Plan and Elevation.
Holiday Inn and the Bank of California in Los Angeles during the San Fernando earthquake 1971 were studied and analyzed, Figures 6 and 7 [15].
2. Method Formulation
A structure fails when the actual building drift δ is higher than the maximum allowable drift Δ. The building margin of safety M is given by the following equation:
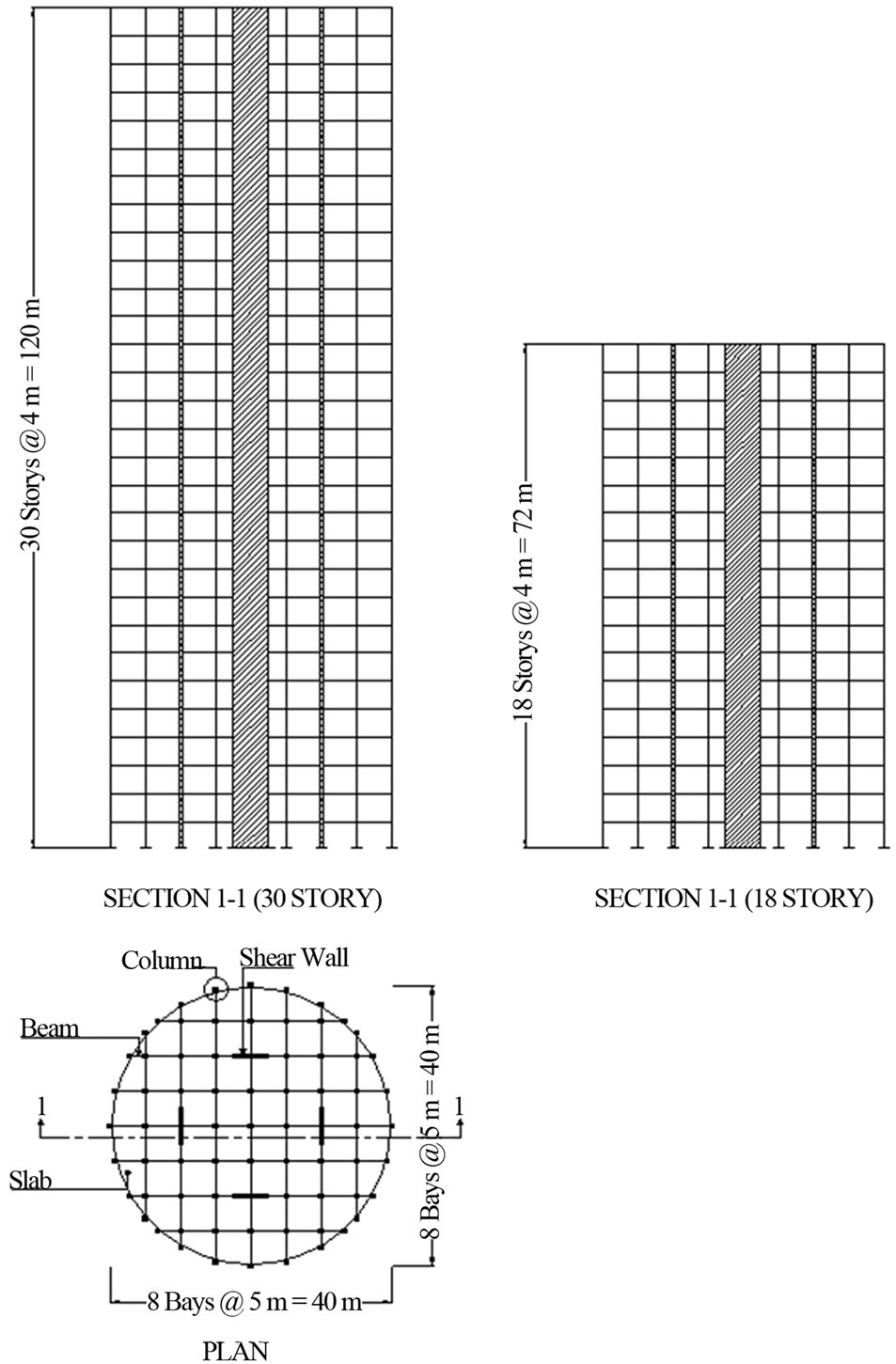
Figure 3. Circular Building Plan and Elevation.
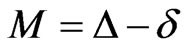 (1)
(1)
The allowable drift D is given by the following equation:
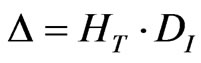 (2)
(2)
where HT = building total height, DI = drift index (1/500 to 1/200), and d = actual building roof displacement.
Hence the probability of failure (pf) of the building is given by the following equation:
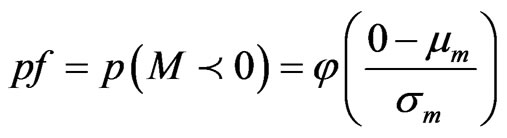 (3)
(3)
where j = standard normal cumulative probability distribution function, mm = mean value of M, and sm = standard deviation of M.
The parameter mm is given by the following equation:
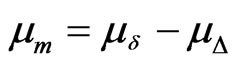 (4)
(4)
The standard deviation of M is given by the following equation:
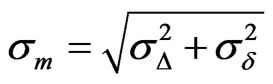 (5)
(5)
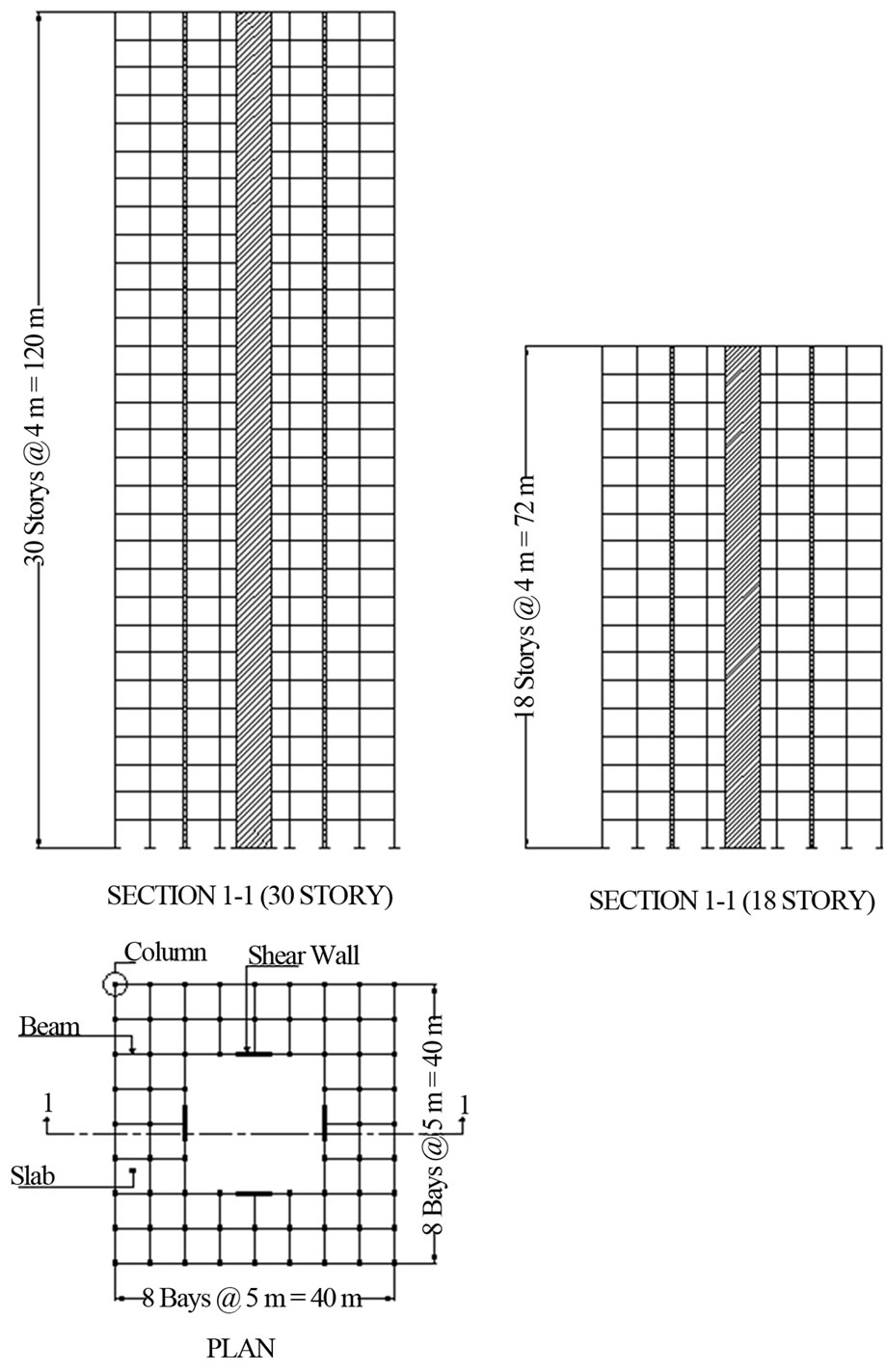
Figure 4. Tube Building Plan and Elevation.

Figure 5. 7-Story Building (US-Japan Research Program).
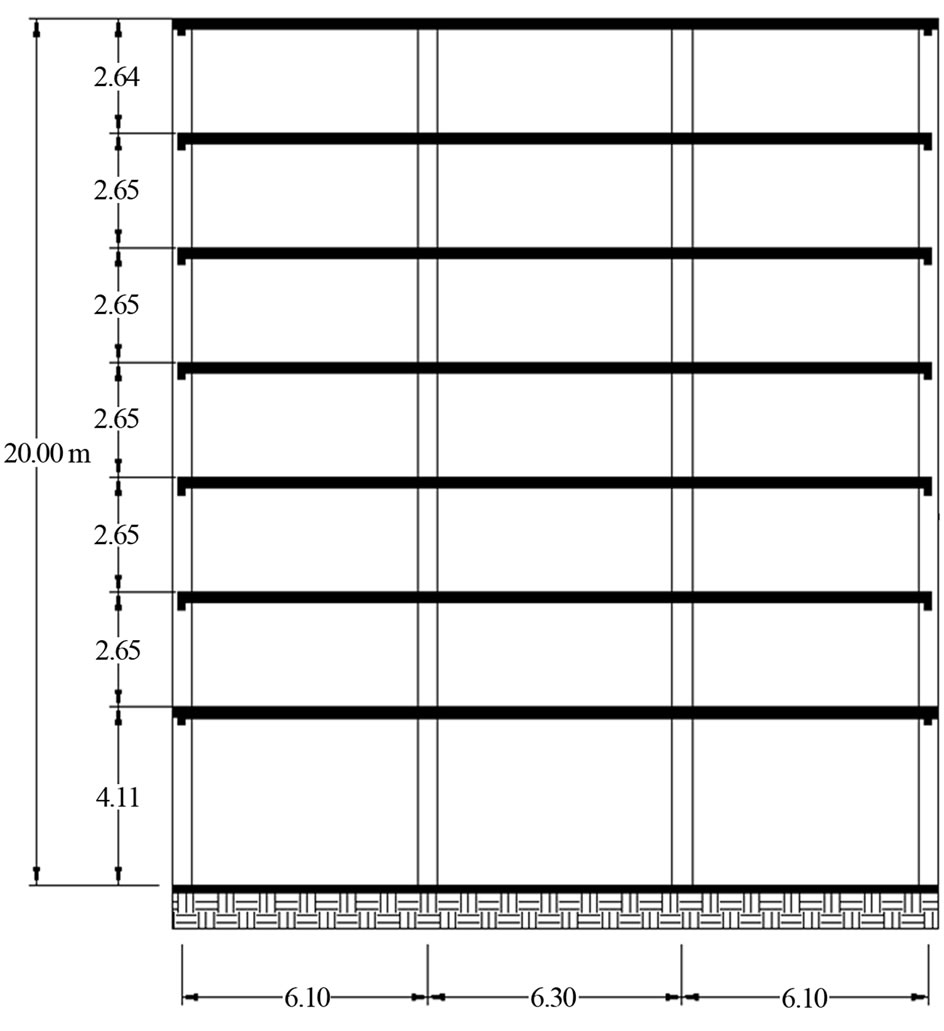
Figure 6. 7-Story Holiday Inn Building.
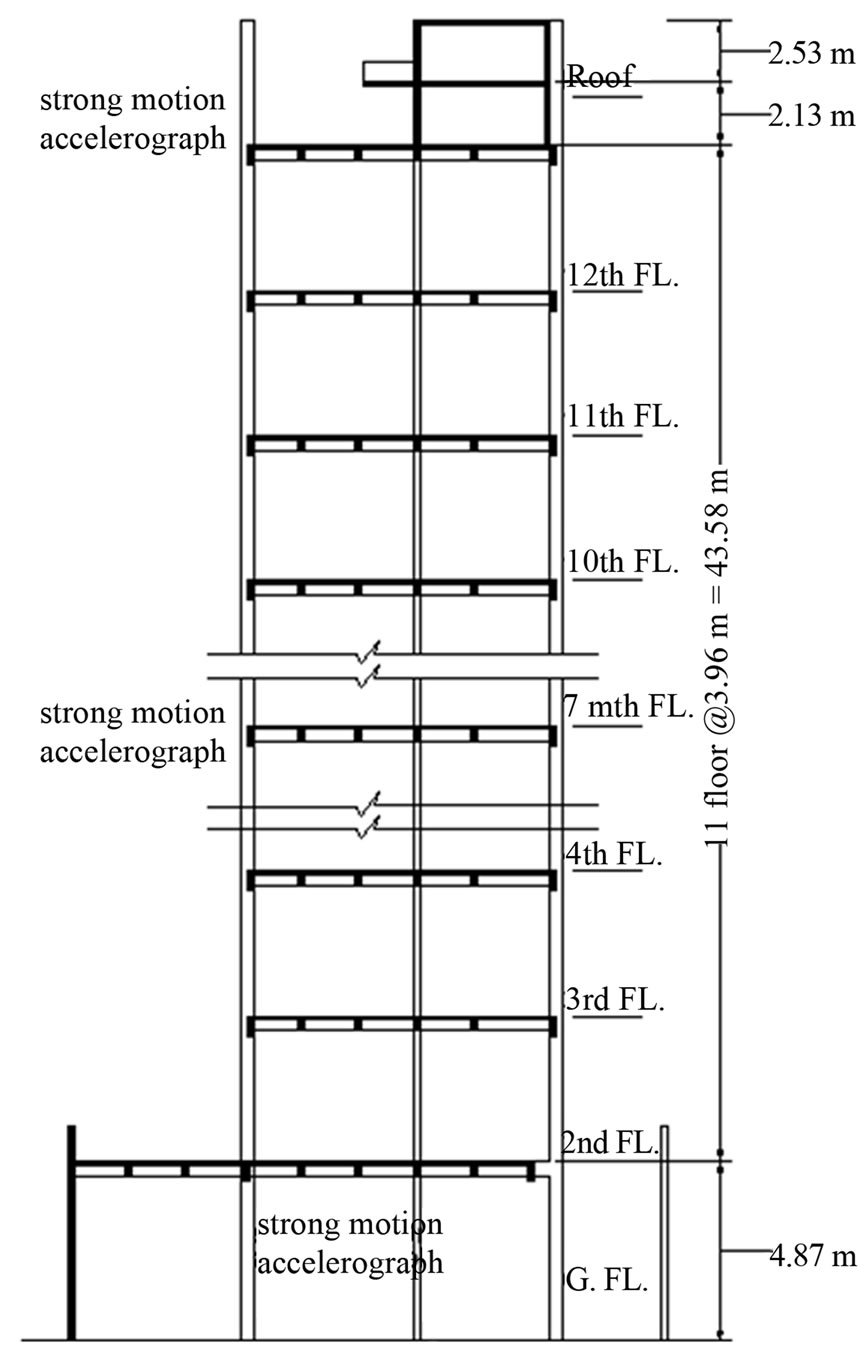
Figure 7. Bank of California Building Transverse Section.
Combining Equations (3)-(5) yields the following equation for the probability of failure (pf) of the building:
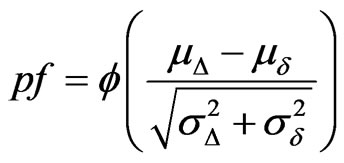 (6)
(6)
Let us define the reliability index β using the following equation:
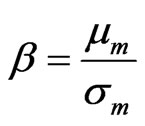 (7)
(7)
Combining Equations (4)-(7) yields the following equation for the probability of failure (pf) of the building:
 (8)
(8)
Combining Equations (4)-(6) and (8) yields the following equation for the reliability index b:
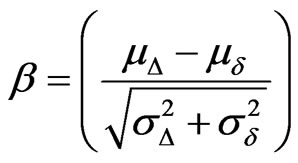 (9)
(9)
By setting the maximum allowable drift Δ equal to mD, the building earthquake response δ equal to md, and the standard deviation equal to the mean value times the coefficient of variation [16], Equation (9) can be re-written as follows.
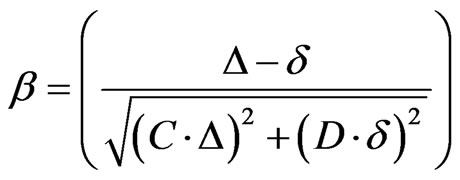 (10)
(10)
The parameter C is given by the following equation:
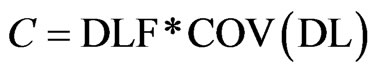 (11)
(11)
where DLF = dead load factor, which is equal to 1.2 as prescribed by ACI Code [17] and COV (DL) = coefficient of variation for dead load, which is equal to 0.13 as suggested by [16].
On the other hand, the parameter D is given by the following equation:
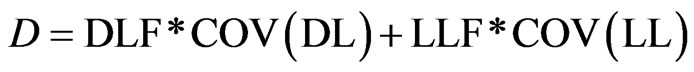 (12)
(12)
where LLF = live load factor, which is equal to 1.6 as prescribed by ACI Code and COV (LL) = coefficient of variation for live load, which is equal to 0.37 as suggested by [17].
The displacement d for a certain β is obtained by re-writing Equation (10) as follows.
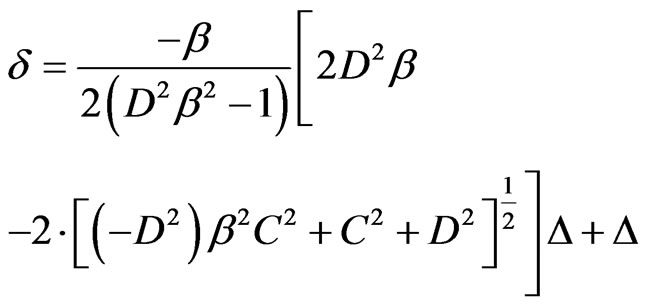 (13)
(13)
The maximum reliability index bmax, which is obtained by setting δ equal to zero in Equation (13), is given by the following equation:
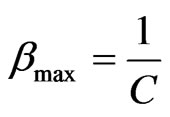 (14)
(14)
The formulation presented herein allows the estimation of the reliability of structures based on drift results when subjected to static equivalent earthquake loads defined by UBC and IBC codes of design for different seismic zones and soil profiles. The reliability index β is calculated for multi story buildings based on their top response to earthquake loading and the allowable drift (Δ) (i.e., on desired drift).The allowable and computed drifts are inserted into Equation (13) to determine the building reliability index β. Since the reliability index β is a function of the building height, the drift index, the roof displacement, and the dead and live load factors required by the code of design, the reliability index model can be used for all types of concrete and steel buildings. The reliability index β is in fact flexible because it can be used for all local and international design codes simply by changing the parameters magnitudes of the reliability index equation to the required parameters by the design code. Each design code has its unique reliability index β as a magnitude and the interaction chart that corresponds to it. The interaction chart is a very useful tool in determining the building drift for the desired level of reliability during the preliminary design of the building members.
3. Result and Discussion
Several steel and reinforced concrete buildings were simulated using STAAD PRO [18] as shown in Figure 8. The buildings, which have square, rectangular, and circular shapes and different heights, include reinforced concrete shear walls and slabs. The buildings were subjected to static equivalent earthquake loads, which are defined by UBC and IBC codes of design, for different seismic zones and soil profiles and their responses were obtained using the finite element software STAAD-PRO.
The reliability index β was computed for 18- and 30- story buildings in seismic zones 1, 2, 3 and 4 and for soil profiles S1, S2 and S3 for each zone. The results show that the reliability index β of the buildings with a drift limit index of 0.005 lied in the range of 3.5 and 6 for 18-story buildings and in the range of 2.3 and 5.8 for 30-story buildings. The buildings with a β value less or equal to 6 are considered as reliable while those with a β value less than 3.5 are considered as unreliable building (see Table 2 and Figures 9 and 10).
Increasing the building strength will also increase its reliability. For example increasing the size of columns and shear wall will increase the level of reliability as shown in Table 3.

Figure 8. 30-Story Concrete Building Finite Element Model.
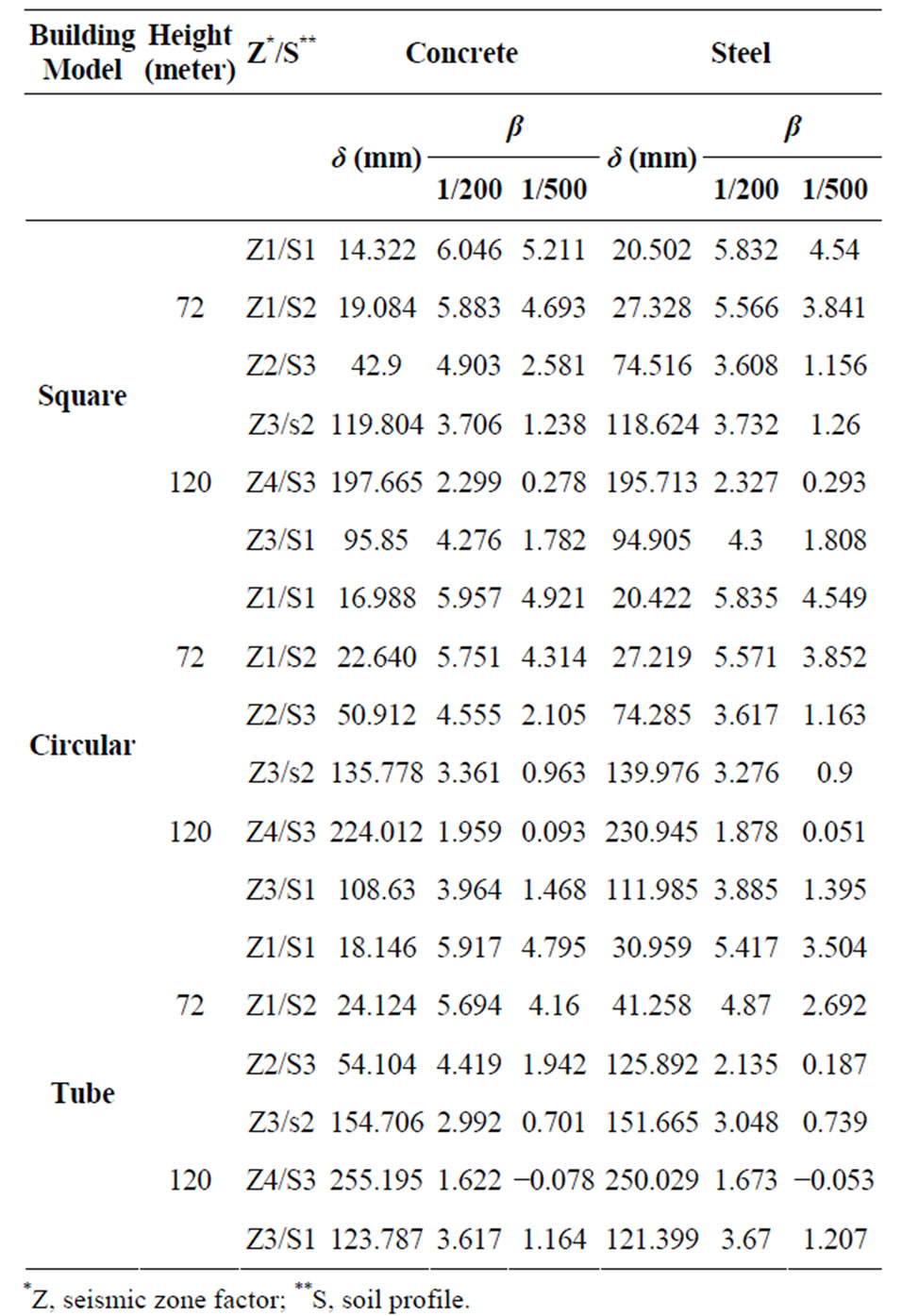
Table 2. Building Model Reliability Indexes.
4. Case Study
A case study dealing with the performance of actual building sunder seismic load is considered herein to further validate the use of their liability index β approach. The reliability index β was computed using Equation (10) to assess the building reliability in each seismic test. The first building is the 23.06-meter-high seven-story reinforced concrete building in Japan, which was tested statically and dynamically by the US-Japan Research Panel.
The building was subjected to a static test SL-3 and three dynamic earthquake tests SPD-1, SPD-3, and SPD-4. For each test, the reliability index β of the building were computed using Equation (10) for two drift indexes, namely, (1/200) and (1/500). The top displacement used in Equation (10) was the building actual top displacement recorded during each test. Table 4 summarizes the building reliability index results obtained for the static and dynamic tests. The results shows that the reliability indexes b of the building during the static test for both drift limits are equal to −0.862 and −1.147, respectively. This indicates that the building is not reliable for a top displacement of 326 mm. This finding is in agreement with the actual status of the building after the test. It has been reported that the building actually failed and the main reinforcing bars of the boundary columns were fractured and the concrete was crushed along the full span of the shear wall. The values of the building reliability index b of the building for the dynamic earthquake tests SPD-1 were high indicating a reliable building. This finding agreed with the real building status during the test. Both SPD-3 and SPD-4 tests yielded low values of the reliability index indicating an unreliable building. These two findings are in agreement with the actual status of the building after the tests.
The reliability indexes of the Holiday Inn and the Bank of California buildings in Los Angeles during the San Fernando earthquake 1971 were computed to assess the reliability of the building. The Holiday Inn building is located approximately 8 miles from the San Fernando 1971 earthquake center. The seven story reinforced concrete frame building, which extends 20 meters above grade, suffered a considerable damage, which is in agreement with the computed low value of its reliability index (see Table 5).
The Bank of California building is a 12-story reinforced concrete frame building located approximately 23 kilometers from the center of San Fernando earthquake. The building, which has a height of 52.727 m, suffered a considerable damage, which is in agreement with the computed low value of its reliability index (see Table 5).
The displacement formula (Equation (13)), which is based on a simple iteration calculation, can be used to
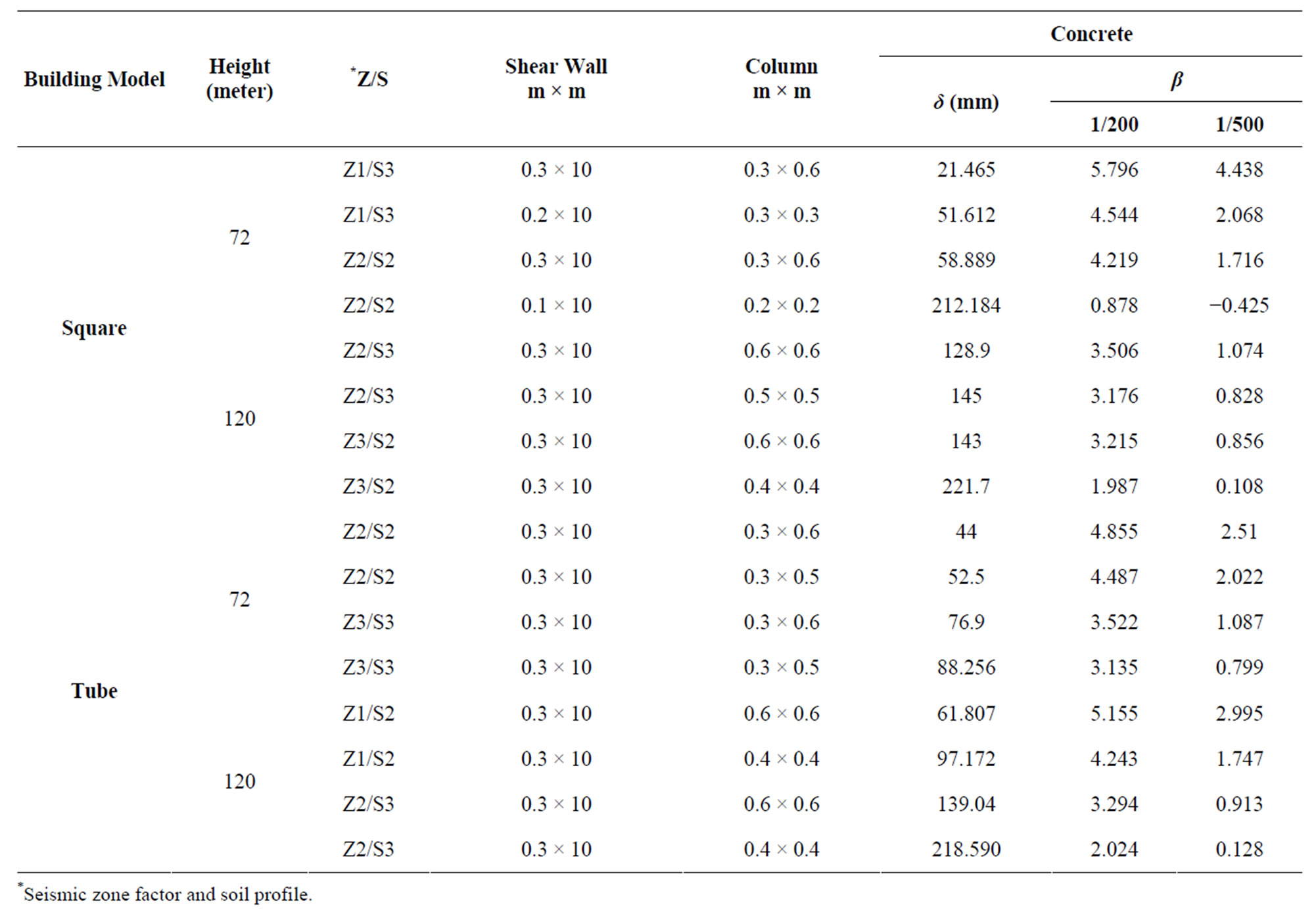
Table 3. Member Sizes and Reliability Indexes.
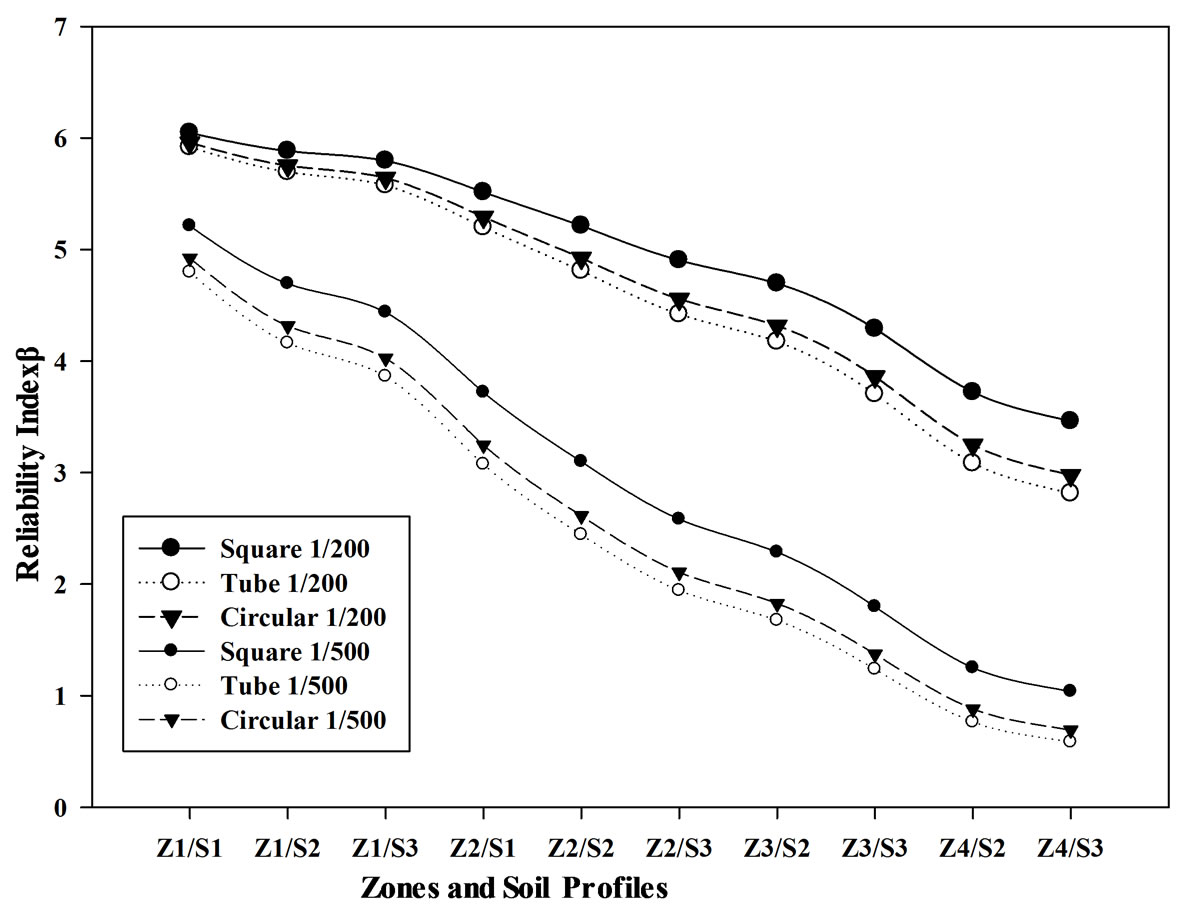
Figure 9. 18-Story Concrete Building Model Reliability Index.
compute the top building drift. An interaction chart that relates the maximum allowable drift (Δ) to the actual or computed building top drift (δ) is provided, Figure 11.
For example, a building with a total height of 120 meters, a drift index of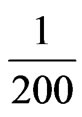 , and a desired reliability in-
, and a desired reliability in-

Figure 10. 30-Story Steel Building Model Reliability Index.
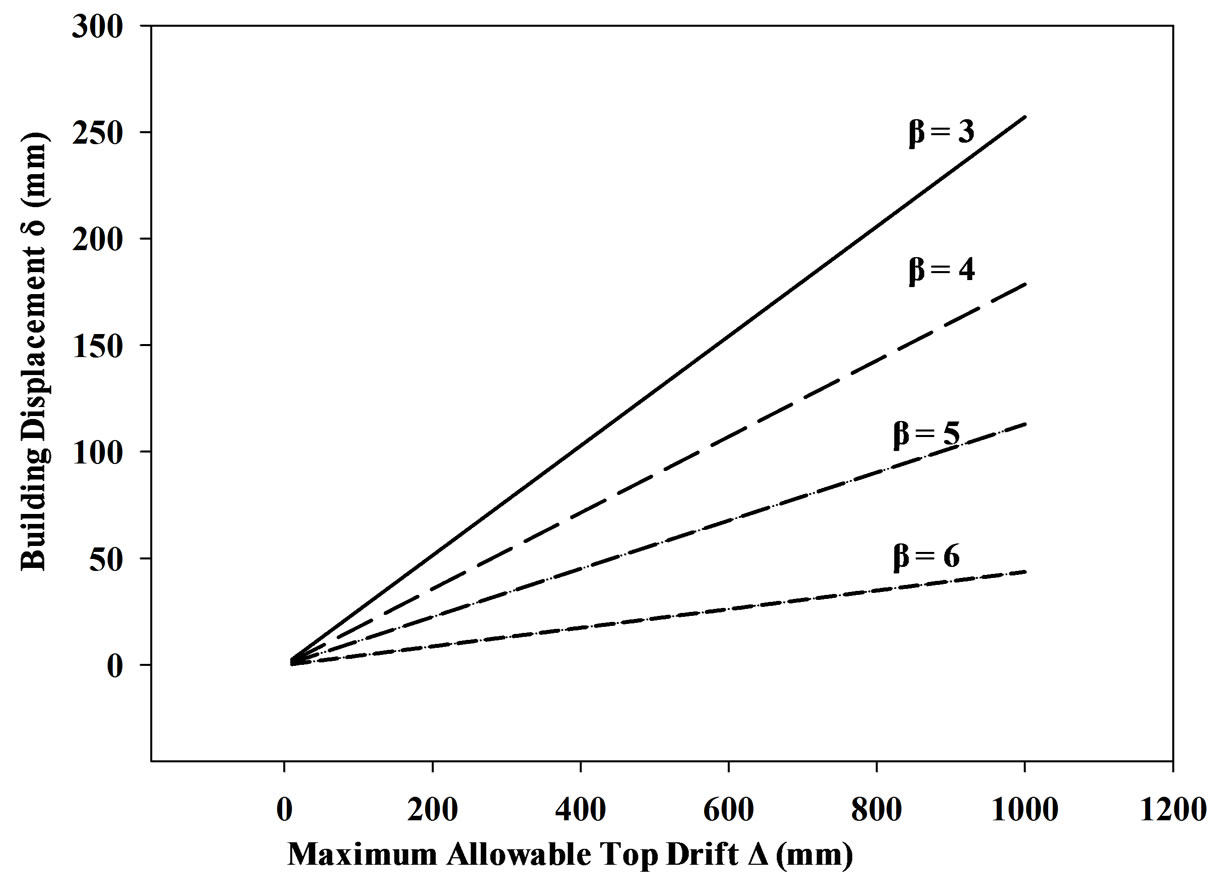
Figure 11. Interaction Chart.
dex of 3 will have 156 mm top drift (roof displacement) based on the interaction chart (see Figure 11 and Table 6). The interaction chart is a very useful tool in determining the required top drift for the desired building reliability. In other words the building should be designed to have a roof displacement less or equal to the top drift δ obtained using the interaction chart.
5. Conclusion
The paper developed a reliability index approach to assess the reliability of concrete and steel buildings subjected to earthquake loading. The assessments obtained using the reliability index of the simulated, tested, and
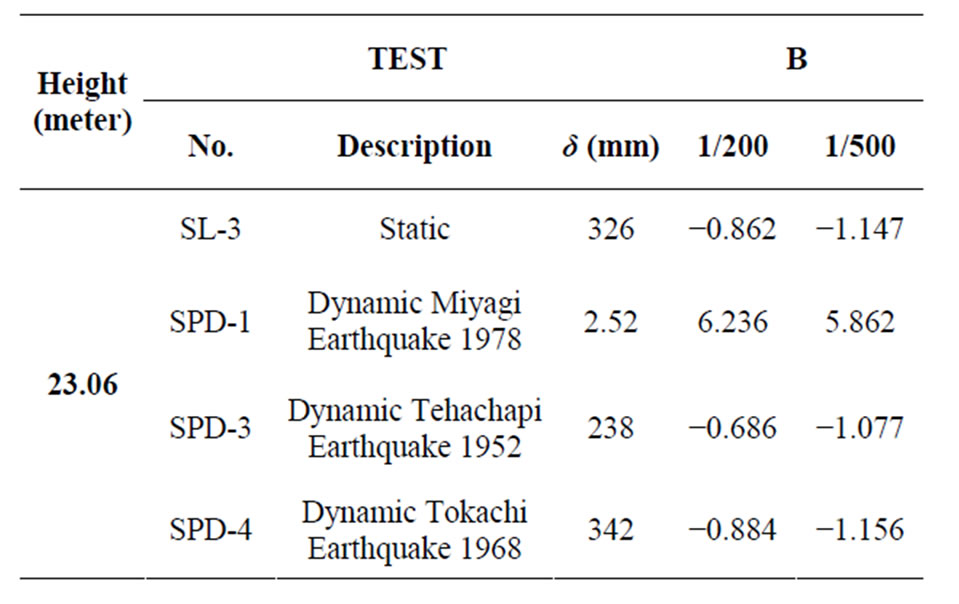
Table 4. US-Japan Research Program.
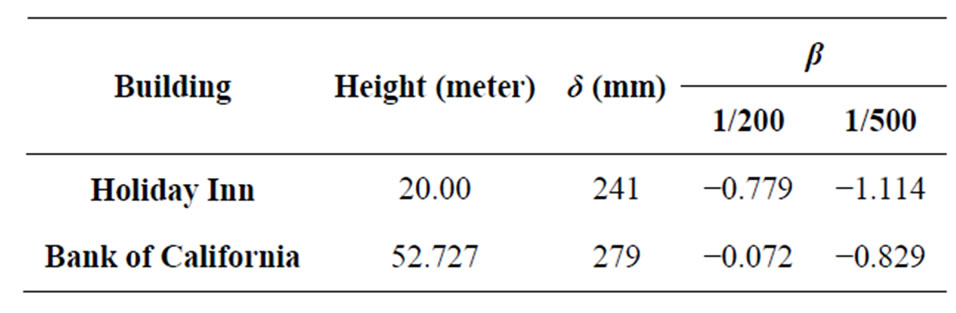
Table 5. Holiday Inn and Bank of California Buildings.
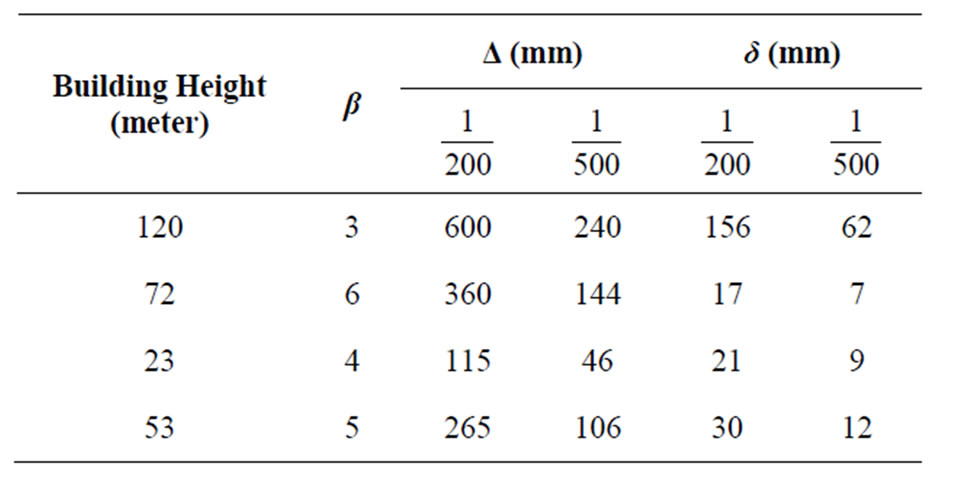
Table 6. Top Drift Interaction Chart.
actual buildings in earthquake zones were acceptable as indicators of the buildings reliability. The reliability index model is flexible and can be used for: 1) all types of buildings and 2) all local and international design codes simply by changing the parameters magnitudes of the reliability index equation to the required parameters by the code of design. Each design code will have its unique reliability index β as a magnitude and the interaction chart that corresponds to it. The interaction chart is a very useful tool in determining the building drift for the desired level of reliability during the preliminary design of the building members.
6. Acknowledgments
This research work is supported by Qatar University Internal Grant QUUG-CENG-CA-12/10-2.
REFERENCES
- S. G. Buonopane and B. W. Schafer, “Reliability of Steel Frames Designed with Advanced Analysis,” Journal of Structural Engineering, Vol. 132, No. 2, 2006, pp. 267- 276. doi:10.1061/(ASCE)0733-9445(2006)132:2(267)
- A. El Ghoulbzouri, A. Khamlichi, M. Bezzazi and A. Lopez, “Reliability Analysis for Seismic Performance Assessment of Concrete Reinforced Buildings,” Australian Journal of Basic and Applied Science, Vol. 3, No. 4, 2009, pp. 4484-4489.
- R. Ranganathan and C. Deshpande, “Reliabilty Analysis of Reinforced Concrete Frames,” Journal of Structural Engineering, Vol. 113, No. 6, 1987, pp. 1315-1328. doi:10.1061/(ASCE)0733-9445(1987)113:6(1315)
- M. S. Roufaiel and C. Meyer, “Reliability of Concrete Frames Damaged by Earthquakes,” Journal of Structural Engineering, Vol. 113, No. 3, 1987, pp. 445-457. doi:10.1061/(ASCE)0733-9445(1987)113:3(445)
- S. Terada and T. Takahash, “Failure-Conditioned Reliability Index,” Journal of Structural Engineering, Vol. 114, No. 4, 1988, pp. 942-953. doi:10.1061/(ASCE)0733-9445(1988)114:4(942)
- P. H. Waarts, “Structural Reliability Using Finite Element Methods,” Delft University Press, Netherlands, 2000.
- International Conference of Building Officials, “Uniform Building Code,” 1997.
- International Code Council, “International Building Code,” 2009.
- D. C. Epaarachchi, M. G. Stewart and D. V. Rosowsky, “Structural Reliability of Multistory Buildings during Construction,” Journal of Structural Engineering, Vol. 128, No. 2, 2002, pp. 205-213. doi:10.1061/(ASCE)0733-9445(2002)128:2(205)
- M. S. Al-Ansari, “Drift Optimization of High-Rise Buildings in Earthquake Zones,” Journal of Tall and Special Building, Vol. 2, 2009, pp. 291-307.
- J. W. Lindt and G. Goh, “Earthquake Duration Effect on Structural Reliability,” Journal of Structural Engineering, Vol. 130, No. 5, 2004, pp. 821-826. doi:10.1061/(ASCE)0733-9445(2004)130:5(821)
- J. W. Lindt, “Damage-Based Seismic Reliability Concept for Woodframe Structures,” Journal of Structural Engineering, Vol. 131, No. 4, 2005, pp. 668-675. doi:10.1061/(ASCE)0733-9445(2005)131:4(668)
- R. E. Melchers, “Structural Reliability Analysis and Prediction,” Wiley, New York, 1999.
- J. K. Wight, “Earthquake Effects on Reinforced Concrete Structures, U.S.—Japan Research, SP84,” American Concrete Institute, Detroit, 1985.
- D. A. Foutch, G. W. Housner and P. C. Jennings, “Dynamic Responses of Six Multistory Buildings during the San Fernando Earthquake,” Earthquake Engineering Research Laboratory, California, 1975.
- B. Ellingwood, T. V. Galambos, J. G. MacgGregor and C. A. Cornell, “Development of a Probability Based Load Criterion for American Standard A58: Building Code Requirements for Minimum Design Loads in Buildings and Other,” 1980.
- American Concrete Institute (ACI), “Building Code and Commentary,” 2008.
- Bentley System Inc., “STAAD PRO V8i. Three Dimensional Static and Dynamic Finite Element Analysis and Design of Structures,” 2009.

