ABSTRACT

This work focuses on the optimization of investment contributions of pension asset with a view to improving contributors’ participation in achieving better return on investment (RoI) of their funds. We viewed some new regulations on Nigeria’s Contributory Pension Scheme” (CPS) from amended legislation of 2014, some of which are yet to be implemented when their regulations are approved. A mathematical model involving 5 variables, 5 inequality constraints covering regulatory limitations and limitation on scarce resource known as Asset Under Management (AUM), suggested and mathematically shown to be possible through “maximization of return irrespective of risk” while obeying all regulatory controls as our constraints optimized. Optimized portfolio using MatLab shows that the portfolio representing AES 2013 portfolio with a deficit growth of ₦15.75 m representing 3.27% less than the portfolio’s full growth potential within defined assumptions would have been averted if contributors actually set their targets and investment managers optimize from forecasts of future prices using trend analysis.

Keywords:

Optimization Portfolio, Contributory Pension Scheme, Return Rate, Pension Reform

1. Introduction

The Nigerian contributory pension industry is in its 11th year with Asset Under Management in excess of N5T. In 2004, the initial Pension Reform Act (PRA 2004) came into force in June 2004. The focus is to achieve well-throughout goals which include;

1) Pension to be contributory and fully funded.

2) Personalized and portable individual Retirement Savings Account (RSA).

3) The management of pension funds privately and the separation of the functions management of assets.

4) Trust in the expertise of investment but on regulation.

5) The inclusion of life insurance covers for employees by employer.

6) Provision of superior and strict central regulator and supervisor of all pension management and payments.

With the 6 above points and more in view, a well-organized and manned Pension Commission (PenCom) headed (2004-2012) by Mr. Muhammed K. Ahmad Ahmad started off in 2004. After the licensing of the initial 7 Pension Fund Administrators (PFAs) and 3 Pension Fund Custodians (PFCs) in December 2005, the contributory pension industry started off operationally with signing contributor into account in 2006. Operational challenges and obstacles where met with resolvable items resolved. Reactions of stakeholders including and especially the contributing members were regularly logged in for eventual review and rework. Amongst such reviews include:

1) Regulatory approval for resigned contributing members to access 25% of RSA balance after 4 months from date of resignation or termination.

2) Review of compulsory enrolment of employees per private sector employer if 15 and above.

3) Review of rate of contribution to the scheme as follows.

a) A minimum of 10% by the employer as against previous minimum of 7.5%.

b) A minimum of 8% by the employer against a maximum of 7.5% in previous 2004 act.

4) Restriction on the rate of pension fund asset allowing for the use of some fraction of RSA balance as equity contribution for residential mortgage.

5) The introduction of pension protection fund etc.

In all of these reviews, the need of most contributors is often resident in how much their contributions have added over the period of contribution. This borders on Return on Investment (RoI).

Important of note is that the longest contributor retiring in 2016 has barely contributed for 10 years’ operational period of Nigeria’s CPS. It is also important to put into account the regulation on the ratios of contributors’ exposure to approved asset classes and their securities risk-return measurements before qualifying to be included as a component of pension portfolio. From inception, there has been strict regulation of Nigeria’s pension asset portfolio beginning with unit investment across all classes of contributors. Aside strict regulations on securities inclusion into Nigeria’s pension portfolio, Pension Fund Administrators (PFAs) seem to have only one motivation to drive high return on investment. This is to acquire more new enrollees-members and increase magnitude of their asset management fees. For this reason, there seem to be less pressure on investment managers in balancing between risk and return. It is common to see most PFAs (Pension Fund Administrators) not exposing their funds up to 25% allowable exposure to Equity-variable income security. The reason may be found in two parts;

a) Non-participation of contributing members in requesting a target rate of return.

b) Non-reduction of asset management fees irrespective of investment managers’ performance satisfying contributor’ required rate of return, specified at the start of contribution.

Herein, we look into some mathematical models of production output, minimization of risk, and optimization of scarce resources for maximum output.

Optimization of picking routebased on backtracking algorithm was apply in [1] , where the optimization method under the environment of VC++6.0 wasverified. Instead we show using MatLab that portfolio representing AES 2013 with a deficit growth of ₦15.75 m representing 3.27% less than the portfolio’s full growth potential is found within defined assumptions. This would have been averted if contributors’ actually set their targets and investment managers optimize from forecasts of future prices using trend analysis as in [2] . We also recommend that Nigeria’s Pension Commission begins working to empower contributors through regulation, to have provisions of requesting and setting reasonable targets of Return on their investments [3] . This, if introduced, adds to necessary conditions for PFAs to be qualified to earn asset management fees and to what fraction of maximum allowable, based on percent (%) of contributors’ RoI request achieved.

2. Contributors and Investment Portfolio

In February 2015, a draft suggestion on investment of pension fund assets is suggesting a multi-fund regime which may allow pension assets to be invested across 4 different portfolios satisfying defined-age-distribution of contributing members. Also, in Q4 2015, industry portfolio is shown in Tables 1-3 (Source: PenCom Pension Industry Portfolio as at Q1 2015).

Source: Portfolio of an AES member fund as at December 2013.

A typical example of a portfolio on the basis of Table 2 is in Table 3. Table 3 displays a portfolio whose total wealth (AUM) is =N=481,172,022.25 with a unit price of =N=1.509. This means that one unit of this portfolio is selling at this time for N1.51k approximately. Another significant fact is the value of the portfolio relating to its unit price from which we can resolve its accounting units. This is the portfolio we be re-optimizing to achieve a 15% return from a more optimized distribution of assets across the available scarce resources (AUM).

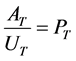(1)

where;

A_T = Asset Under Management as at time T.

U_T = No of accounting units at time T.

P_T = Price of accounting units at time T.

For all

From (1), U_T = (481,172,022.25)/(1.1509) = 318,868,139.33 Units of account.

A pension portfolio manager focuses on optimization considering application of any of the following:

1) Minimize risk for a specified risk.

2) Maximize the expected return for a specified risk.

3) Minimize the risk and maximize the expected return using specified risk aversion factor.

4) Minimize the risk regardless of the expected return.

5) Maximize the expected return regardless of the risk.

To achieve any of the above, we look at two basic important focus areas which are:

a) Security and market analysis. By this we access attributes of the entire set of possible investment.

b) Creating an optimal portfolio of assets. This involves the determination of the Best risk-return opportunities available from feasible investment portfolio and the choice of best portfolio from the feasible set.

To illustrate (a) and (b) above, let us consider the consolidated portfolio from Table 4 (Source: Consolidated AES-portfolio December 31, 2013).

3. The Mathematical & Mathematical Formulations

We calculated expected returns from portfolio elements in their asset classes. To minimize risk, we need to also compute standard deviation. In this case we applied Harry Markowitz variance or standard deviation as a means of risk measurement [4] . That is;

(2)

Such that the following conditions

1)

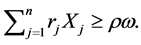
2)

3)

Forming with i and j security/asset over a period “T” we have;

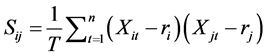(3)

Equation (3) is the covariance of these securities/assets i and j and

X_jt = each security/asset average return over the period T.

r_j = jth security/asset average return over the period T.

X_j = Portfolio allocation of security/asset j not greater than asset upper limit or global limit µ.

Ρ = The minimum return required by a particular investor or trustee of a portfolio.

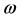= Total Asset Under Management contained in the portfolio.

We note that the validity of this model is in two parts; the expected return is multivariate normally distributed and the investor prefers lower risk with a preference of risk aversion.

If we apply Minimum Absolute Deviation in estimation output (Return on Investment plus initial Asset Under Management). Let us say as follows;

L(A) = {x: x produces A}. where x, A are inputs and output vector respectively. The input level set L(A) satisfies the following properties;

1)

2)

3)

Let us say we input, Equity, Bond, & Money Market returns with expectation of output equal to A (Asset Under Management) L(E, B, M) Î A.

Let Ф(x), 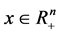be a frontier optimization function. As an optimization problem Ф(x) may be expressed as,

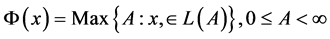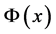, succeeds properties from

1) Ф(0) = 0, Maximum output produced by a null vector is zero

2) , maximum output produced by a larger input vector.

3) Ф(x) is concave function of x.

Input Level

Let

where

then

.

Consider now the Cobb Douglas production frontier given by;

(4)

This is the decision making unit. Taking logarithm on both sides of (4)

.

If

then

(5)

If there are k asset classes making decision of AUM growth (k growth-decision making units), then introducing slack variables, , the inequality is converted equation;

.

Taking summation on both sides implies

(6)

By dividing (6) by k, we have

(7)

Minimizing of (2) is same as minimizing of (7) (being a constant).

Minimization of (5) implies

(8)

Combining (7) and (8) we obtain a linear programing problem (LPP) for which decision variables are α and α_j as:

(9)

, is conditional for sign.

Let , then the LPP can be expressed as follows:

(10)

With two errors “and” one sided and the two-sided disturbance term, the Minimum Absolut Deviation (MAD) model is given by,

(11)

where.

For ith decision making unit the MAD model implies

Taking Modules on both sides, we have

where

Thus the optimization problem equal to MAD estimated model is given by,

(12)

The decision variable of the above linear programming are, and and the optimal solution of LPP (9) tells DMU specific technical efficiency.

For efficiency estimation, consider the Cobb Douglas production function.

(13)

and define.

Let the random variable z follow Weibull distribution as in [5] so that;

Let

Define or, where.

Notice that

Recall that

Therefore

where.

The probability density function of (for) is given by,

(14)

Here, k is shape parameter of the distribution. k < 1 implies that a greater proportion of DMUs are efficient. k = 1 implies uniform sufficiency and k > 1 implies that a greater proportion of DMUs are inefficient.

The average level of efficiency of the industry comprising of several DMU is,

.

Put, then

Note: For, we have, which coincides with as in [6] for.

By the Least Square Method the Cobb-Douglas production specification is

(15)

We have,

Let

(16)

By [7] we write

(17)

4. Forecast Model & Solution to Contributor Request

From Table 5, values are inputted into Equation (12) and further which are transformed equations into linear forms. This leverages into the avoidance of large covariance ma-

trix required to solve optimization through Markowitz model [8] . We will therefore, set the pension investment outcome of 2013 into its linear form for optimization. Here is setting the request of fund contributors to be that, investment manager grows portfolio by 15% which is better that earlier growth of less than 12%. The question is that from growth rates, how the portfolio assets will be allocated to achieve 14% growth rate by end of next period.

Portfolio Equation

(18)

(No arbitrage or short selling)

General representation of above could be written as,

(19)

Solution to (19) using the interior point method for LP could be associated to the following process;

Let and further, the linear programming problem,

Where (lb = Lower bound, uB = Upper bound).

We now setting to achieve;

(20)

We can then introduce slack variables and but can now rewrite the LP as

Using single matrix representation gives [8] ;

(21)

This, without a problem from constants of objective function, we have the dual of the LP as;

(22)

Introducing a slack, as in minimization function, we have;

(23)

From both dual and original LP, we arrive at optimal solution; Noting that a vector (X^*, w^*, S^*) is a solution of the primal-dual if and only if it satisfies the Karush-Kuhn Tucker (KKT) optimality condition. The KKT condition here can be written as;

(24)

Solving for X_is from iterations using Tora optimization software [9] , we were able to get solution at the 6^th iteration from solution matrix under,

(25)

Subject to

(26)

where;

X₁ is the value of exposure of the portfolio to equity stocks.

X₂ is the value of exposure of the portfolio to money market securities.

X₃ is the value of exposure of the portfolio to FGN bond W_iX.

X₄ is the value of exposure of the portfolio to state bonds.

X₅ is the value of exposure of the portfolio to corporate bond.

5. Result from MatLab Programing

function Z = PhDObjective(x)

%UNTITLED Summary of this function goes here

% Detailed explanation goes here

Z = −1.09*x(1) − 1.124*x(2) − 1.1043*x(3) − 1.13*x(4) − 1.118*x(5);

end

function [c,ceq] = PhDConstraint

%UNTITLED2 Summary of this function goes here

% Detailed explanation goes here

c(1) = x(1) + x(2) + x(3) + x(4) + x(5) − 481.71;

c(2) = 0.75*x(1) − 0.25*x(2) − 0.25*x(3) − 0.25*x(4) − 0.25*x(5) − 0;

c(3) = −0.35*x(1) + 0.65*x(2) − 0.35*x(3) − 0.35*x(4) − 0.35*x(5) − 0;

c(4) = 0.8*x(1) − 0.8*x(2) + 0.2*x(3) − 0.8*x(4) + 0.2*x(5) − 0;

c(5) = −0.2*x(1) − 0.2*x(2) − 0.2*x(3) + 0.8*x(4) − 0.2*x(5) − 0;

c(6) = −0.95*x(1) + 0.05*x(2) + 0.05*x(3) + 0.05*x(4) + 0.05*x(5) − 0;

ceq = [];

functioncreatefigure(yvector1, X1, Y1, Y2, Y3, X2, Y4, Y5)

%CREATEFIGURE(YVECTOR1,X1,Y1,Y2,Y3,X2,Y4,Y5)

% YVECTOR1: bar yvector

% X1: vector of x data

% Y1: vector of y data

% Y2: vector of y data

% Y3: vector of y data

% X2: vector of x data

% Y4: vector of y data

% Y5: vector of y data

% Auto-generated by MATLAB on 06-Sep-2016 06:54:07

% Create figure

Figure 1 = figure('PaperSize',[20.98 29.68],'NumberTitle','off',...

'Name','OptimizationPlotFcns');

% uicontrol currently does not support code generation, enter 'doc uicontrol' for correct input syntax

% In order to generate code for uicontrol, you may use GUIDE. Enter 'doc guide' for more information

% uicontrol(...);

% uicontrol currently does not support code generation, enter 'doc uicontrol' for correct input syntax

% In order to generate code for uicontrol, you may use GUIDE. Enter 'doc guide' for more information

% uicontrol(...);

% Create subplot

subplot1 = subplot(3,2,1,'Parent', Figure 1,'XTick',[1 2 3 4 5]);

% Uncomment the following line to preserve the X-limits of the axes

% xlim([0 6]);

box('on');

hold('all');

% Createxlabel

xlabel('Number of variables: 5','Interpreter','none');

% Createylabel

ylabel('Current point','Interpreter','none');

% Create title

title('Current Point','Interpreter','none');

% Create bar

bar(yvector1,'EdgeColor','none','Tag','optimplotx','Parent',subplot1);

% Create subplot

subplot2 = subplot(3,2,2,'Parent', Figure 1);

hold('all');

% Createxlabel

xlabel('Iteration','Interpreter','none');

% Createylabel

ylabel('Function evaluations','Interpreter','none');

% Create title

title('Total Function Evaluations: 241','Interpreter','none');

% Create plot

plot(X1,Y1,'Parent',subplot2,'Tag','optimplotfunccount',...

'MarkerFaceColor',[1 0 1],...

'Marker','diamond',...

'LineStyle','none',...

'Color',[0 0 0]);

% Create subplot

subplot3 = subplot(3,2,3,'Parent', Figure 1);

hold('all');

% Createxlabel

xlabel('Iteration','Interpreter','none');

% Createylabel

ylabel('Function value','Interpreter','none');

% Create title

title('Current Function Value: -497.4613','Interpreter','none');

% Create plot

plot(X1,Y2,'Parent',subplot3,'Tag','optimplotfval',...

'MarkerFaceColor',[1 0 1],...

'Marker','diamond',...

'LineStyle','none',...

'Color',[0 0 0]);

% Create subplot

subplot4 = subplot(3,2,4,'Parent', Figure 1);

hold('all');

% Createxlabel

xlabel('Iteration','Interpreter','none');

% Createylabel

ylabel('Constraint violation','Interpreter','none');

% Create title

title('Maximum Constraint Violation: 0','Interpreter','none');

% Create plot

plot(X1,Y3,'Parent',subplot4,'Tag','optimplotconstrviolation',...

'MarkerFaceColor',[1 0 1],...

'Marker','diamond',...

'LineStyle','none',...

'Color',[0 0 0]);

% Create subplot

subplot5 = subplot(3,2,5,'Parent', Figure 1);

hold('all');

% Createxlabel

xlabel('Iteration','Interpreter','none');

% Createylabel

ylabel('Step size','Interpreter','none');

% Create title

title('Step Size: 0.00056679','Interpreter','none');

% Create plot

plot(X2,Y4,'Parent',subplot5,'Tag','optimplotstepsize',...

'MarkerFaceColor',[1 0 1],...

'Marker','diamond',...

'LineStyle','none',...

'Color',[0 0 0]);

% Create subplot

subplot6 = subplot(3,2,6,'Parent', Figure 1);

hold('all');

% Createxlabel

xlabel('Iteration','Interpreter','none');

% Createylabel

ylabel('First-order optimality','Interpreter','none');

% Create title

title('First-order Optimality: 3.7195e-007','Interpreter','none');

% Create plot

plot(X2,Y5,'Parent',subplot6,'Tag','optimplotfirstorderopt',...

'MarkerFaceColor',[1 0 1],...

'Marker','diamond',...

'LineStyle','none',...

'Color',[0 0 0]);

5.1. Analysis of Result

Table 5 satisfied the contributor’s request of 15% growth provided allocation and diversification was according to optimized allocation in Table 5. Optimal and feasible solution was reached at the 37^th iteration, There is smooth convergence and zero (0) iteration violation according to the results from TORA optimization software. There is no violation of rules of interior point method. Referring to Table 3 and allocation resulted in a reduced income of 497.46 - 481.71 equating to a loss of 15.75 million. Also, visibly FGN bond which enjoyed allocation of 73.4% in Table 3 is reduced to 40% in optimized portfolio of Table 5. Other calibrations in MatLab optimized portfolio against Table 3 portfolio include equity changed from 15.95% allocation to 5%. This is due to required regulation of minimum equity investment, money market security changed from 1.67% to 34.9982% to enjoy its full regulatory allocation of a maximum of 40%. State bond is modified from 7.15% to 19.9982% reaching its limit of 20% with a contribution of 16.6% rate of return.

5.2. Assumptions

Here, we assumed that all economic growth indicators are kept constant from opening value to closing value period. This is because we are using retrospective rate of return for a corrective forecast of would have been a better output using “Contributor required Rate of Return” to build portfolio asset allocation. This work is also using investment strategy of “Maximize return irrespective of expected risk” it is for the investors who are not risk averse.

6. Conclusions & Recommendation

Our expectation in this study was met. We could see that there is a possibility to allocate funds across the asset classes within their individual regulatory ratios to AUM and still achieve 15% return instead of 11% in actual result. We then can recommend that contributors should be empowered to request a minimum rate of return at least twice a year. Pension Fund Administrators should be regulated to take only a percent achievement multiplied by 1.6% asset management fees rate as income for managing pension fund.

Within the boundaries of available data and inherent values and deficiencies in this work, we are recommending that Nigeria’s Pension Commission begin a study on how pension contributors are to be empowered with instruments of requesting on regulated periods of instruments maturity what is their reasonable expected rate of return on their volumes of investment. This clearly defines and regulates pension managers from earning asset management fees even when they practically either did not satisfy 50% of contributors.

Cite this paper

Osu, B.O. and Egbe, G.A. (2016) Optimization of Pension Asset Portfolio in Nigeria with Contributors’ Specified Return Rate. Open Journal of Optimization, 5, 103-119. http://dx.doi.org/10.4236/ojop.2016.54012

References