Received 9 February 2015; accepted 12 May 2015; published 14 May 2015

ABSTRACT

To enhance the optimization ability of particle swarm algorithm, a novel quantum-inspired particle swarm optimization algorithm is proposed. In this method, the particles are encoded by the probability amplitudes of the basic states of the multi-qubits system. The rotation angles of multi-qubits are determined based on the local optimum particle and the global optimal particle, and the multi-qubits rotation gates are employed to update the particles. At each of iteration, updating any qubit can lead to updating all probability amplitudes of the corresponding particle. The experimental results of some benchmark functions optimization show that, although its single step iteration consumes long time, the optimization ability of the proposed method is significantly higher than other similar algorithms.

Keywords:

Quantum Computing, Particle Swarm Optimization, Multi-Qubits Probability Amplitudes Encoding, Algorithm Design

1. Introduction

In 1999, Dr. Eberhart and Dr. Kennedy proposed particle Swarm Optimization (particle swarm optimization, PSO) [1] . As a new optimization tool, it is now widely used in combinatorial optimization [2] and numerical optimization [3] . In PSO’s performance improvement, some commonly used strategies are as follows: selecting the appropriate control parameters [4] ; designing reasonable update rules of the particle velocity and position [5] ; combining PSO with the other algorithms [6] ; and employing quantum computation to design the update strategy [7] . These approaches enhance the PSO performance in different degrees. Quantum computing is an emerging interdisciplinary, combining the information science and quantum mechanics, and its integration with intelligent optimization algorithms begun in the 1990s; there is quantum-behaved particle swarm optimization algorithm [8] , quantum-inspired evolutionary algorithm [9] , quantum-inspired harmony search algorithm [10] , quantum-inspired immune algorithm [11] , quantum-inspired genetic algorithm [12] , and quantum-inspired derivative differential evolution algorithm [13] . In the algorithm mentioned above, Ref. [8] applied real-based code method; the other references employed single qubit probability amplitude to code individuals. In these kinds of coding, the adjustment of a qubit can only change one gene on the individual. However, in the multi-qubits probability amplitude-based code, with application of coherence quantum states, simply adjusting a qubit can change all probability amplitudes of the ground state in multi-bit quantum superposition states, and then update all genes on the individual. In this paper, we propose a new multi-qubits probability amplitude encoding-based quantum-inspired particle swarm optimization. Standard function extreme optimization experiments show the superiority of the proposed algorithm.

2. Basic PSO Model

There is M particles in the n-dimensional space. For the 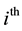particle, its position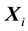, velocity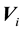, self-opti- mum position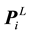, global optimum position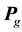, are written as: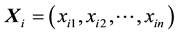;;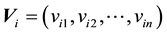;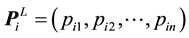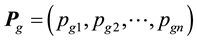. The update strategy of particles can be described as follows.

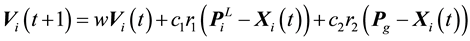(1)

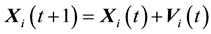(2)

where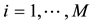, 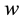is the inertia factor, 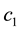is itself factor, 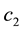global factor, , is an uniformly distributed random number in (0, 1).

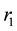For convenience of description, Equation (1) can be rewritten as follows.

(3)

where

(4)

(5)

To make the PSO convergence, all particles must approximation.

3. Multi-Bit Quantum System and the Multi-Bit Quantum Rotation Gate

3.1. Qubits and Single Qubit Rotation Gate

What is a qubit? Just as a classical bit has a state―either 0 or 1―a qubit also has a state. Two possible states for a qubit are the state and, which as you might guess correspond to the states 0 and 1 for a classical bit.

Notation like is called the Dirac notation, and we will see it often in the following paragraphs, as it is the standard notation for states in quantum mechanics. The difference between bits and qubits is that a qubit can be in a state other than or. It is also possible to form linear combinations of states, often called superposition.

(6)

where is the phase of, and denote the probability amplitude of.

In the quantum computation, the logic function can be realized by applying a series of unitary transform to the qubit states, which the effect of the unitary transform is equal to that of the logic gate. Therefore, the quantum services with the logic transformations in a certain interval are called the quantum gates, which are the basis of performing the quantum computation. A single qubit rotation gate can be defined as

(7)

Let the quantum state, and can be transformed by. It is obvious

that shifts the phase of

3.2. The Tensor Product of Matrix

Let the matrix has m low and n column, and the matrix has p low and q column. The tensor product of and is defined as.

(8)

where is the element of matrix.

3.3. Multi-Bit Quantum System and the Multi-Bit Quantum Rotation Gate

In general, for an n-qubits system, there are of the form ground states, similar to the single- qubit system, n-qubits system can also be in the a linear superposition state of ground states, namely

(9)

where is called probability amplitude of the ground state, and to meet the following equation.

(10)

Let, according to the principles of quantum computing, the can be written as

(11)

It is clear from the above equations that, in an n-qubits system, any one of the ground state probability amplitude is a function of n-qubits phase, in other words, the adjustment of any can update all 2ⁿ probability amplitudes.

In our works, the n-qubits rotation gate is employed to update the probability amplitudes. According to the principles of quantum computing, the tensor product of n single-qubit rotation gate is n-qubits rotation gate. Namely

(12)

where,.

Taking as an example, the can be rewritten as follows.

(13)

It is clear that

(14)

where

4. Particle Encoding Method Based on Multi-Bits Probability Amplitudes

In this paper, the particles are encoded by multi-qubits probability amplitudes. Let N denote the number of particles, denote the dimension of optimization space. Multi-qubits probability amplitudes encoding method can be described as follows.

4.1. The Number of Qubits Needed to Code

For an n-bits quantum system, there are probability amplitudes, which can be used directly as a result of an individual encoding. In the D-dimensional optimization space, it is clear that. Due to the constraint relation between each probability amplitude (see to Equation (10)), hence. For the D-dimensional optimization problem, the required number of qubits can be calculated as follows.

(15)

4.2. The Encoding Method Based on Multi-Qubits Probability Amplitudes

First, generating randomly N n-dimensional phase vector, , as follows

(16)

where, rand is a random number uniformly distributed within the (0,1),.

Let, using Equation (11), we can obtain following n-qubits systems, , ,. In each of the quantum system, the first D probability amplitudes can be regarded as a D-dimensional particle code.

5. The Update Method Based on Multi-Qubits Probability Amplitudes

In this paper, the multi-bit quantum rotation gates are employed to update particles. Let the phase vector of the

global optimal particle be, the phase vectors of the i^th particle be, and

the itself optimum the phase vector be.

From Equation (11), it is clear that, once has been updated, all its corresponding probability amplitudes will be updated. To improve the search capability, in an iteration, all phases are updated in turn, which allows all particles are updated n times. Let the denote the phase update step size, the specific update can be described as follows.

Step 1. Set,.

Step 2. Set.

Step 3. Determine the value of the rotation angle, where the sgn donates the symbolic function.

If, then.

If, then.

If, then.

If, then.

Step 4. Compute the rotation angles, and update all particles according to the following equation, ,. where r1 and r2 denote random numbers between the interval (0, 1).

Step 5. If, then, back to step 2.

6. Quantum-Inspired Particle Swarm Optimization Algorithm Encoded by Probability Amplitudes of Multi-Qubits

Suppose that, N denote the number of particles, denote the number of optimization space dimension. For multi-qubits probability amplitudes encoding quantum-inspired particle swarm optimization, called MQPAP-SO, the optimization process can be described as follows.

1) Initialize the particles swarm

According to Equation (15) to determine the number of qubits n, according to Equation (16) initialize phase of each particle, according to Equation (11) to calculate the probability amplitude of each particle, where the first D probability amplitudes are the coding of the particles. Set the probability amplitude of the particle be, coding result can be expressed as the following equation.

(17)

Initialization phase update step, the limited number of iteration G. Set the current iteration step.

2) Calculation of the objective function value

Set the j-dimensional variable range be, because of the probability amplitude values in the interval [0, 1], it is need to make the solution space transformation. The transformation equation is below.

(18)

where,.

Calculate the objective function values of all particles. Let the i^th particle phase be, the

objective function value is, global optimal particle phase be, global optimal objec-

tive function value be, the particle itself optimal phase is, Its optimal objective function value is.

3) Update the particle position

For each particle, accordance to step 1 - step 5 in Section 5, update repeatedly n times. Using the Equation (11) to calculate the probability amplitude, using Equation (18) to implement the solution space transformation and calculate the value of the objective function. Let the objective function value of the particle be. If, then,.

4) Update the global optimal solution

Let the optimal particle phase be, the corresponding objective function value be. If, then, , otherwise,.

5) Examine termination conditions

If, back to (3), otherwise, save and, end.

7. Comparative Experiment

In this study, the 20 standard test functions are employed to verify the optimization ability of MQPAPSO, and compare with the general particle swarm optimization (PSO) [14] , quantum delta potential-well particle swarm optimization, QDPSO [15] , shuffled frog leaping algorithm, SFLA [16] . All functions belong to minimum optimization, where D is the number of independent variables, Ω is the solution space, is the exact minimum point, is the corresponding minimum.

7.1. Test Function

(1);;;

(2);;;

(3);;;

(4);;;

(5);;;

(6);;;

(7);;;

(8);; ;

(9);;;

(10);;;

(11);;;.

(12); ;;,

(13);;;

(14);

;;

(15); ;;

(16);;; ;

(17);;;;;;

(18);;;

(19);;;

(20);;

7.2. The Experimental Scheme and Parameter Design

The dimension of all test functions is set to (for) and. Population size of these four algorithms is set to. For PSO, QPSO and SFLA, the limited iteration number is set to and, respectively, and for MQPAPSO, set to.

For SFLA, according to Ref. [16] , the biggest jump step is set to. Because of the sub-group number of SFLA is related to the specific problem, we consider some different a variety of groupings, and the best results are used to compare with other algorithm. Specifically, we take the following six cases:

,

where the first number denotes the number of sub-group and the second number denotes the number of frog in sub-group. For each of combination, the SFLA is independent run 30 times, and the average optimization result over 30 runs and the average time of a single iteration are recorded. In these six groups, the best optimization results and the corresponding average time of a single iteration are regarded as a comparison index.

For PSO, according to Ref. [14] , ,. For QDPSO, according to Ref. [15] , the control parameters is set to. For MQPAPSO, phase update step take. Each function is optimized independently 30 times by these three algorithms, and the average optimization results and the average time of a single iteration are taken as a comparison index.

7.3. Comparative Experiment Results

Experiments conducted using Matlab R2009a. Taking as an example, the average time of a single iteration, the results of such comparison are shown in Table 1, the average optimization results for and, are shown in Table 2 and Table 3.

For the function, let the average time of four algorithms for a single iteration be, , , , respectively, and the average optimization results be, , , , respectively. To facilitate comparison, taking MQPAPSO and QDPSO as an example, the ratio of the average time of a single iteration and the ratio of the average optimal results are defined as follows.

(19)

For four algorithms, the ratios of the average time of a single iteration are shown in Table 4, and the ratios of the average optimization results are shown in Table 5.

From Table 1 and Table 4, for single iteration mean time, MQPAPSO is nearly 10 times longer than QDPSO, PSO, and SFLA. To make the comparison fair, we must further investigate the optimization results under the same running time. This is the fundamental reason why the iteration steps of for QDPSO, PSO, SFLA are set to and. From Table 2 and Table 3, the average results of MQPAPSO are far less than the other three algorithms in both and, where shows that the use of multi-bit probability

amplitude coding and evolutionary mechanisms can indeed improve the optimization capability. From Table 5, in the same iteration steps, the optimization result of MQPAPSO is only one thousandth of that of QDPSO. On the other hand, in the same running time, the optimization result of MQPAPSO is only nine percent of QDPSO. Experimental results show that multi-bit probability amplitude coding method can indeed significantly improve the optimization ability of the traditional PSO algorithm and other similar algorithms.

8. Conclusion

In this paper, a quantum-inspired particle swarm optimization algorithm is presented encoded by probability amplitudes of multi-qubits. Function extreme optimization results show that under the same running time, the optimization ability of proposed algorithm has greatly superior to the traditional methods, revealing that the multi-qubits probability amplitude encoding method indeed greatly enhances the ability of traditional particle swarm optimization performance.

Funding

This work was supported by the Youth Foundation of Northeast Petroleum University (Grant No. 2013NQ119) and the National Natural Science Foundation of China (Grant No. 61170132).

References