Open Journal of Optimization Vol.04 No.01(2015), Article ID:54434,8
pages
10.4236/ojop.2015.41001
Mathematical Model for Dynamic Pump-Wavelength Selection Switch
Nattapong Kitsuwan, Dwina Fitriyandini Siswanto, Eiji Oki
Department of Communication Engineering and Informatics, The University of Electro-Communications, Tokyo, Japan
Email: kitsuwan@uec.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 February 2015; accepted 3 March 2015; published 6 March 2015
ABSTRACT
This paper presents a mathematical model based on dynamic pump-wavelength selection for an optical packet switch (OPS). In the OPS, multiple packets that carry the same wavelength from different input ports could be addressed to the same output port at the same time slot. This condition is called wavelength contention. Of those contended packets, only one is forwarded to the output fiber while the others are dropped. Parametric wavelength conversion is used to convert the contended wavelengths into available non-contending wavelengths. The OPS based on the dynamic pump-wavelength selection scheme, where the pump-wavelengths are adjusted based on the requests in every time slot, uses a heuristic matching algorithm to minimize the number of packet losses. However, there is no guarantee that the heuristic algorithm outputs the optimum result. The mathematical model presented in this paper is used to confirm the performance of the heuristic matching algorithm for the DPS-based OPS. A simulation shows that the heuristic matching algorithm achieves the same performance as the optimum solution provided by the mathematical model.
Keywords:
Optical Packet Switching, Wavelength Converter, Optimization

1. Introduction
Optical packet switched (OPS) networks are emerging as a serious candidate for the evolution of optical telecommunication networks needed to support high-throughput services such as voice over IP (VoIP) and high quality video streaming on demand. In an optical packet network with OPSs interconnected with optical fibers running wavelength division multiplexing (WDM), packets are transmitted from source to destination without any optical-electrical-optical (O/E/O) conversion.
In an OPS, an optical fiber carries several wavelengths to transmit packets. An input fiber may carry as many packets as wavelengths, which could be destined to one or several output fibers. In an OPS, output contention occurs when multiple packets from different input fibers share the destination of a single output fiber even though they use the same wavelength at the same time. Only one of the contending packets is forwarded to the output fiber, the others are dropped. To select packets (and wavelengths), a switch configured by a scheduler can be used. In an OPS, the set of aggregated wavelengths coming from an input fiber is optically demultiplexed into individual wavelengths and each wavelength is assigned to an input port of the switch fabric that connects outputs to inputs. The outputs of the switch fabric are assigned different wavelengths. Therefore, each input port of the switch fabric can be connected to an output port of the same wavelength. The set of individual wavelengths of an output fiber are then aggregated before they egress the switch. In the switch fabric, the scheduler decides which inputs and outputs to interconnect for each wavelength by performing a matching process (i.e., the assignment of one input to one output). The case wherein several inputs of the same wavelength have packets for the same output is said to be output contention.
Some methods proposed for resolving output contention use 1) optical buffering through fiber delay lines (FDLs) [1] [2] to store packets. Unfortunately, feasible FDLs are delays smaller than those the packets would need to secure contention-free transmission; 2) deflection routing [3] , which can reduce the need to buffer packets. In this approach, one packet is sent to the designed output while the others are sent to any available output as alternative routes. However, the network control demanded by this approach is overly complex and packet re-sequencing is required as packets may arrive out of order at the destination.
A practical approach to avoiding contention is to use wavelength conversion [4] . A signal with one wavelength is converted to another wavelength. The wavelength of a contending packet that will not be selected is converted into another available wavelength and connected to the same output fiber. A full wavelength converter (FWC) [5] can convert a wavelength to any other wavelength. However, this approach is too expensive for practical applications as dedicated FWCs must be provisioned. To reduce cost of wavelength conversion, the so-called share per node (SPN), in which all converters at the switching node are shared, is considered to be a cost-effective solution [6] [7] . Tunable wavelength converters may be used. However, conversion capability is not be efficient since only one wavelength can be converted at a time.
A parametric wavelength converter (PWC) [8] is an alternative approach to wavelength
conversion because multiple wavelengths, multiple channels, can be converted simultaneously.
To define both the original wavelength,
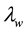 , requiring
conversion, and the new wavelength,
, requiring
conversion, and the new wavelength,
 , a continuous
pump-wavelength,
, a continuous
pump-wavelength,
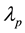 , is set to
, is set to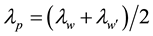 . That is, the
selection of
. That is, the
selection of
 defines the conversion pair of and
defines the conversion pair of and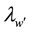 . Because a conversion wavelength pair comprises the set of wavelengths
converted from and converted to, each wavelength can play either role, the source
wavelength or the converted wavelength in a time slot. For example, if
. Because a conversion wavelength pair comprises the set of wavelengths
converted from and converted to, each wavelength can play either role, the source
wavelength or the converted wavelength in a time slot. For example, if
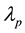 is set to convert
is set to convert
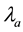 to/from
to/from , where
, where
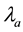 and
and
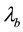 are transmission wavelengths, then
are transmission wavelengths, then
 can be selected to be the original wavelength and
can be selected to be the original wavelength and
 can be selected to be the converted wavelength or vice versa, with the condition
that just one direction is possible at a time. Note that each pair in the set can
have independent conversion directions at a given time.
Figure 1 shows examples of the wavelength conversion pairs in a PWC. There
are seven
can be selected to be the converted wavelength or vice versa, with the condition
that just one direction is possible at a time. Note that each pair in the set can
have independent conversion directions at a given time.
Figure 1 shows examples of the wavelength conversion pairs in a PWC. There
are seven
Figure 1. Example of wavelength conversion pairs in PWC.
wavelengths in this example,
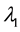 to
to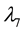 . When
. When



Multiple wavelength conversion based on a parametric process appears to be becoming feasible. The simultaneous multiple wavelength conversion of over 30 channels has been reported using fiber [9] and LiNbO3 waveguides [10] . A high-capacity field transmission experiment using multi-wavelength conversion has also been demonstrated [11] . Moreover, the parametric process is fully transparent to various types of advanced modulation formats such as DPSK [12] and QPSK [13] . These studies show that guard bands can be provided with a suitable channel spacing. With this in mind, this paper assumes that guard bands are provided in the adopted channel spacing, such that they are assumed to be provisioned in the remainder of this paper.
Several studies describe OPSs that use PWCs [14] -[20] . A dynamic pump-wavelength selection (DPS) switch was proposed as an alternative approach to pump-wavelength selection [17] [18] . The set of pump-wavelengths is dynamically changed in every time slot depending on the conversion pairs needed, so that the total number of successful packets can be maximized. The DPS switch combines a matching scheme to connect input ports, output ports and dynamic pump-wavelength selection.
A heuristic matching algorithm was introduced for the DPS-based OPS [17] [18] . Simulation results showed that the DPS switch provides low packet loss rates. However, there is no guarantee that the heuristic matching algorithm does provide the optimum solution. Moreover, the performance offset from the optimum solution has not been confirmed.
In this paper, a mathematical model for the DPS-based OPS is proposed as a reference with which to confirm the performance of the heuristic matching algorithm in [18] . Mathematical modeling is a convenient tool for solving optimization problems. After proposing a mathematical model, the optimum solution of the DPS switch can be obtained. The objective of the mathematical model is to maximize the number of successful packet requests, which in turn minimizes the number of packet losses. The result shows that the heuristic matching algorithm achieves the same performance as the optimum solution provided by the mathematical model.
2. Dynamic Pump-Wavelength Selection Switch
A dynamic pump-wavelength selection (DPS) switch, is an OPS using PWCs where the
set of pump-wavelengths is dynamically changed in every time slot based on requests.
For the general case, the set of pump-wavelengths is defined as


The DPS switch, whose set of pump-wavelengths can be altered on a time slot basis, consists of three parts: the controller, the pump-wavelength generator, and the main switch (see Figure 2).
The controller performs both matching between input and output ports and selecting pump-wavelengths in an integrated manner on a time slot basis. It controls both the switching configuration and pump-wavelength selection by using a matching scheme. It uses electrical signals to communicate with the pump-wavelength generator and the main switch.
The pump-wavelength generator sets pump-wavelengths that are determined by the controller in every time slot. Figure 2 shows a possible implementation approach to the generation of pump-wavelengths. Tunable laser diodes (TLDs) are used to generate pump-wavelengths for PWCs, one TLD for each PWC. A guard time is needed to separate the time slots considering the time needed for switching and for setting pump-wavelengths. A tunable external-cavity laser requires 0.8 ns for wavelength tuning [21] , while a switch using PLZT optical switching technology [22] requires 2.5 ns for optical switching. As the time for wavelength tuning is less than that for optical switching, the guard time is mainly determined by the optical switching technology adopted. With a transmission speed of 10 Gbps, the number of required guard-time bits is 25 bits (2.5 ns ´ 10 Gbps). Consider a fixed packet length of 64 bytes. The ratio of the guard-time bits to the number of packet bits is 25/(64 ´ 8) = 0.05. Therefore, the impact of the guard time on bandwidth utilization is not large in this example.
The main switch is an OPS with N input and output fibers and M PWCs. Each fiber carries W different wavelengths. Demultiplexers at the output of PWCs are used. Each demultiplexed wavelength has a one-to-one correspondence with an input port of the switch fabric. The individual wavelengths, coming through individual input ports of the switch fabric, are grouped by an optical coupler before being forwarded to the output fiber. In
Figure 2. DPS switch.
this way, each converted wavelength can be connected to any output.
3. Proposed Mathematical Model for DPS Switch
A mathematical model is a convenient tool for solving optimization problems. In this paper, the problem is modeled as binary integer linear programming (BILP) to maximize number of connections between input and output ports via PWCs, which in turn minimizes the number of packet losses. In the BILP, the variables are required to be 1 or 0 rather than arbitrary integers. The terminology is as follows.





















Objective function

Subject to








Equation (1a) is the objective function of this BILP model. It maximizes the number
of connections between input and output ports via PWCs. Parameter












Equations (1b)-(1i) are constraints of this BILP model. While Equations (1b)-(1d)
define general characteristics of PWC, Equations (1e)-(1i) define the special features
of a PWC based on DPS. Equation (1b) is the constraint that limits the total number
of successful requests so that it does not outnumber the total number of incoming
requests. Equation (1c) is the constraint that defines that each oth output fiber
at






4. Performance Evaluation
In the simulation, the performance of the heuristic matching algorithm of OPS with
DPS-based PWC is confirmed against the optimum solution provided by the proposed
mathematical model, in term of packet loss rate. The packet loss rate is the difference
between the total number of incoming requests and the total number of successful
requests, with regard to the total number of incoming requests. An OPS with



4.1. Uniform Traffic Pattern
We assume that packet arrival at




Figures 3(a)-(d) show that the performance of the mathematical model matches that
of the heuristic algorithm for all parameter combinations examined. Figure 3(a) shows the packet loss rate of the DPS-based OPS
for different














Figure 3. Packet loss rate of heuristic algorithm and mathematical model with uniform traffic.
4.2. Non-Uniform Traffic Pattern
Packet loss rates under non-uniform traffic were examined using four well-known traffic models: unbalanced [23] [24] , power of two (PO2) [25] , diagonal [26] , and hotspot [27] .
The traffic is uniform if the destinations are uniformly distributed among all output
ports [28] [29] . Otherwise, the traffic is non-uniform [30] . For uniform and non-uniform
traffic, packets arriving at





The traffic is uniformly distributed if


The power of the two (PO2) traffic model [25] is represented by matrix


The diagonal traffic [26] is generated using a diagonal probability,





Under hotspot traffic [27] , each input sends a packet to outputs with equal probability
except for a specific output. The traffic is generated based on a parameter called
hotspot probability,




Figures 4(a)-(d) confirm that the packet loss rates of the heuristic algorithm are
the same as those of the mathematical model in every non-uniform traffic pattern
sampled. Figure 4(a) shows the packet loss rate
for different



Figure 4. Packet loss rate of heuristic algorithm and mathematical model with non-uniform traffic.
assigned to output fibers with the same number as the input fiber. As a result,
there is no contention when












5. Conclusion
This paper proposes a mathematical model to confirm the performance of the heuristic matching algorithm based on dynamic pump-wavelength selection for an OPS with PWCs. The objective function of the mathematical model is to maximize the number of connections, which in turn minimizes the number of packets lost in the optical packet switch between input and output ports. Simulation results show that the heuristic matching algorithm achieves the same performance as the optimum solution is provided by the mathematical model for every parameter combination tested under both uniform and non-uniform traffic patterns.
Acknowledgements
This work was supported in part by the Ministry of Education, Science, Sports and Culture, Grant-in-Aid for Scientific Research (B) 23360168, and the Support Center for Advanced Telecommunications Technology Research (SCAT).
References
- Liang, Z. and Xiao, S. (2007) A Quantized Delay Buffer Model for Single-Wavelength Fiber Delay Line Buffer. IEEE Journal of Lightwave Technology, 25, 1978-1985.
- Zhang, L., Lu, K. and Jue, J.R. (2006) Shared Fiber Delay Line Buffers in Asynchronous Optical Packet Switches. IEEE Journal on Selected Areas in Communications, 24, 118-127. http://dx.doi.org/10.1109/JSAC.2006.1613777
- Lee, S., Sriram, K., Kim, H. and Song, J. (2005) Contention-Based Limited Deflection Routing Protocol in Optical Burst-Switched Networks. IEEE Journal on Selected Areas in Communications, 23, 1596-1611. http://dx.doi.org/10.1109/JSAC.2005.851742
- Simmons, J.M. (2002) Analysis of Wavelength Conversion in All-Optical Express Backbone Networks. Proceedings Optical Fiber Communication Conference and Exhibit, Anaheim, 17-22 March 2002, 34-36. http://dx.doi.org/10.1109/OFC.2002.1036186
- Xiao, G. and Leung, Y.W. (1999) Algorithms for Allocating Wavelength Converters in All-Optical Networks. IEEE/ ACM Transaction on Networking, 7, 545-557. http://dx.doi.org/10.1109/90.793026
- Elmirghani, J.M.H. and Mouftah, H.T. (2000) All-Optical Wavelength Conversion: Technologies and Applications in DWDM Networks. IEEE Communications Magazine, 38, 86-92. http://dx.doi.org/10.1109/35.825645
- Oki, E., Shimazaki, D., Shiomoto, K., Matsuura, N., Imajuku, W. and Yamanaka, N. (2002) Performance of Distributed-Controlled Dynamic Wavelength-Conversion GMPLS Networks. Proceedings International Conference on Optical Communications and Networks (ICOCN 2002), Singapore, 11-14 November 2002.
- Yao, S., Mukherjee, B., Yoo, S.J.B. and Dixit, S. (2000) All-Optical Packet-Switched Networks: A Study of Contention-Resolution Schemes in an Irregular Mesh Network with Variable-Sized Packets. Proceedings SPIE OptiComm, May 2000.
- Watanabe, S., Takeda, S. and Chikama, T. (1998) Interband Wavelength Conversion of 320 Gb/s (32 × 10 Gb/s) WDM Signal Using a Polarization-Insensitive Fiber Four-Wave Mixer. Proceedings European Conference on Optical Communication (ECOC’98), Madrid, 85-86.
- Yamawaku, J., Takara, H., Ohara, T., Sato, K., Takada, A., Morioka, T., Tadanaga, O., Miyazawa, H. and Asobe, M. (2003) Simultaneous 25 GHz-Spaced DWDM Wavelength Conversion of 1.03 Tbit/s (103 ch × 10 Gbit/s) Signals in PPLN Waveguide. Electronics Letters, 39, 1144-1145. http://dx.doi.org/10.1049/el:20030719
- Yamawaku, J., Yamazaki, E., Takada, A., Morioka, T. and Suzuki, K. (2006) Field Demonstration of up to 640 Gb/s (64 ch/spl Times/10 Gb/s) GWP Switching Networks with a QPM-LN Wavelength Converter in JGN II Test Bed. IEEE Journal of Selected Topics in Quantum Electronics, 12, 529-535. http://dx.doi.org/10.1109/JSTQE.2006.876625
- Devgan, P., Tang, R., Grigoryan, V. and Kumar, P. (2006) Highly Efficient Multichannel Wavelength Conversion of DPSK Signals. Journal of Lightwave Technology, 24, 3677-3682. http://dx.doi.org/10.1109/JLT.2006.882244
- Yu, J., Huang, M. and Chang, G. (2008) Polarization Insensitive Wavelength Conversion for 4 ´ 112 Gbit/s Polarization Multiplexing RZ-QPSK Signals. Optics Express, 16, 1161-21169. http://dx.doi.org/10.1364/OE.16.021161
- Okonkwo, C., Almeida, R.C., Martin, R.E. and Guild, K.M. (2008) Performance Analysis of an Optical Packet Switch with Shared Parametric Wavelength Converters. IEEE Communications Letters, 12, 596-598. http://dx.doi.org/10.1109/LCOMM.2008.080269
- Kitsuwan, N., Rojas-Cessa, R., Matsuura, M. and Oki, E. (2010) Performance of Optical Packet Switches Based on Parametric Wavelength Converters. Journal of Optical Communications and Networking, 2, 558-569. http://dx.doi.org/10.1364/JOCN.2.000558
- Rojas-Cessa, R., Oki, E. and Chao, H.J. (2004) Maximum Weight Matching Dispatching Scheme in Buffered Clos-Network Packet Switches. Proceedings of the 2004 IEEE International Conference on Communications, Paris, 20-24 June 2004, 1075-1079.
- Kitsuwan, N. and Oki, E. (2010) Optical Packet Switch Based on Dynamic Pump Wavelength Selection. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM2010), Miami, 6-10 December 2010, 1-5.
- Kitsuwan, N. and Oki, E. (2011) Optical Packet Switch Based on Dynamic Pump Wavelength Selection. IEEE/OSA Journal of Optical Communications and Networking, 3, 162-171. http://dx.doi.org/10.1364/JOCN.3.000162
- Kitsuwan, N., Yatjaroen, J. and Oki, E. (2011) Hybrid Pump-Wavelength Configuration for Optical Packet Switch with Parametric Wavelength Converters. Proceedings of the IEEE International Symposium on Access Spaces (ISAS 2011), Yokohama, 17-19 June 2011, 19-22. http://dx.doi.org/10.1109/ISAS.2011.5960913
- Kitsuwan, N. and Oki, E. (2012) Dynamic Pump-Wavelength Selection for Optical Packet Switch with Recursive Parametric Wavelength Conversion. Proceedings of the IEEE International Conference on High Performance Switching and Routing (HPSR2012), Belgrade, 24-27 June 2012, 174-178.
- Kaure, M., Girault, M., Leuthold, J., Honthaas, J., Pellegri, O., Goullancourt, C. and Zirngibl, M. (2003) 16-Channel Digitally Tunable External-Cavity Laser with Nanosecond Switching Time. IEEE Photonics Technology Letters, 15, 371-373. http://dx.doi.org/10.1109/LPT.2002.807948
- Furukawa, H., Wada, N., Takezawa, N., Nashimoto, K. and Miyazaki, T. (2008) 640 (2 ´ 32 ´ 10) Gbit/s Polarization-Multiplexed, Wide-Colored Optical Packet Switching Achieved by Polarization Independent High-Speed PLZT Switch. Proceedings of the Optical Fiber Communication Conference and Exposition and National Fiber Optic Engineers Conference (OFC/NFOEC), San Diego, 24-28 February 2008, 1-3.
- Oki, E., Jing, Z., Rojas-Cessa, R. and Chao, H.J. (2002) Concurrent Round-Robin-Based Dispatching Schemes for Clos-Network Switches. IEEE/ACM Transactions on Networking, 10, 830-844. http://dx.doi.org/10.1109/TNET.2002.804823
- Rojas-Cessa, R., Oki, E., Jing, Z. and Chao, H.J. (2001) CIXB-1: Combined Input-One-Cell-Crosspoint Buffered Switch. Proceedings of the 2001 IEEE Workshop on High Performance Switching and Routing, Dallas, 29-31 May 2001, 324-329.
- Bianco, A., Franceschinis, M., Ghisolfi, S., Hill, A.M., Leonardi, E., Neri, F. and Webb, R. (2002) Frame-Based Matching Algorithms for Input-Queued Switches. Proceedings of the IEEE Workshop on High Performance Switching and Routing (HPSR 2002), Kobe, 26-29 May 2002, 69-76.
- Beldianu, S.F., Rojas-Cessa, R., Oki, E. and Ziavras, S.G. (2009) Re-Configurable Parallel Match Evaluators Applied to Scheduling Schemes for Input-Queued Packet Switches. Proceedings of the 18th International Conference on Computer Communications and Networks, San Francisco, 3-6 August 2009, 1-6.
- Rahmani, A.M., Afzali-Kusha, A. and Pedram, M. (2009) NED: A Novel Synthetic Traffic Pattern for Power/Performance Analysis of Network-on-Chips Using Negative Exponential Distribution. Journal of Low Power Electronics, 5, 1-10. http://dx.doi.org/10.1166/jolpe.2009.1039
- Oki, E. and Yamanaka, N. (1998) A High-Speed Tandem-Crosspoint ATM Switch Architecture with Input and Output Buffers. IEICE Transactions on Communications, E81-B, 215-223.
- Oki, E. and Yamanaka, N. (1997) A High-Speed ATM Switch Based on Scalable Distributed Arbitration. IEICE Transactions on Communications, E80-B, 1372-1376.
- Mekkittikul, A. and McKeown, N. (1997) Scheduling VOQ Switches under Non-Uniform Traffic. CSL Technical Report, CSL-TR 97-747, Stanford University, Stanford.





