Open Journal of Optimization
Vol.03 No.04(2014), Article ID:51600,15 pages
10.4236/ojop.2014.34005
A Mathematical Model for Deriving Optimal Leasing Policies of a Satellite Operator
Elena Sarri, George P. Papavassilopoulos
School of Electrical and Computer Engineering, National Technical University of Athens, Athens, Greece
Email: elena@netmode.ntua.gr, yorgos@netmode.ntua.gr
Academic Editor: Karim Hamza, University of Michigan, USA
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 September 2014; revised 14 October 2014; accepted 30 October 2014
ABSTRACT
This paper presents a dynamic mathematical model of optimal leasing allocation of satellite band- width and services in terms of expected revenues and associated risk. This tool meets the need of a Satellite Operator to determine the optimal leasing policy of the available bandwidth. A methodology and a tool for techno-economic evaluation of satellite services are developed. The output of the tool enables the policy decisions to be customized by the attitude toward risk that the company wants to apply at each time period. The study is based on inputs concerning data and services from an existing Satellite Operator and addresses a real situation. Demand and pricing data have been gathered from the international market. The decision making tool is given in the set-up of a decision tree presenting quantified alternative leasing policies and risks. Sensitivity analysis is also performed to measure the efficiency of the model.
Keywords:
Decision Making Tool, Dynamic Model, Satellite Services, Techno-Economic Evaluation

1. Introduction
The evolutionary penetration of the satellite services and demand in the telecommunication market during the last decades has created the need for decision making tools for a satellite operator [1] [2] . There is still an incremental growth to the telecommunication applications and services [3] [4] . A number of studies have proposed methodologies and tools for the techno-economic evaluation of different aspects of satellite communication dealing with physical, operational, design performance and risk parameters [5] . The need for in-depth analysis of the economic feasibility of new telecommunication solutions that take into account both technological and econometric characteristics of the applications, has become obvious, both in industrial and academic community. This study deals with the creation and assessment of an optimal business policy of a Satellite Operator. The ability of real time decisions has a significant effect to the viability and profitability of the company in the growing and competitive satellite market. The decision making model presented here is an applied tool for assessment purposes, which deals with real problems and can be used as such, by any Satellite Operator. Limited work has addressed the revenue modeling [6] in terms of market penetration, expected profits and risks, in order to provide a quantitative estimation to the Satellite Operator (after the launching) for the optimal business decision making.
The problem of determining the optimal leasing policy for satellite services, at different time periods is similar to an inventory control problem, with evolution in time, incorporating dynamic and stochastic elements [7] [8] , modified accordingly to address the specific application [9] . The purpose of our work is to model and quantify this problem, using heuristic techniques, as well as to evaluate the outcome. The validation of this work results from its usage by the Greek Satellite Operator in the last five years and the development of a new methodology based on stochastic dynamic optimization, presented in [10] with similar results.
We present a model that compares different scenarios of combinations of customers asking to hire satellite capacity. There is a variety of services that a satellite can support. For each of these services requested by a customer, there is a different bandwidth demand, duration of lease, and a different price. The purpose of this work is to find the most profitable case for the incumbent operator. Each scenario leads to a decision tree. This maximization problem is described in terms of real and expected revenues, along with the corresponding probability of getting them. The final outcome leads to optimal enterprise steps that maximize revenues and enable the evaluation of different contingency plans. The decisions are taken successively in a time horizon and thus the presented tool incorporates time evolution. Consequently the model is dynamic.
At the first stage of the work, demand and pricing data have been gathered from the international market. These data provided by the operating Satellite firm i) are statistically processed to produce mean values and standard deviations for each service and each bandwidth demand when needed, and ii) are integrated into a mathematical model, implemented at the second stage, and taking into account all possible states and stages [11] . The model evaluates all probable revenues, along with their associated risks that could result from each alternative decision branch. The concept of the tool gives the benefit of accessing alternative courses of action, to the decision maker. Depending on the company policy at each time period, variant enterprise steps could be followed. Sensitivity analysis is included, in order to determine the impact of small errors in parameters estimates to the final decision. It is performed using both mathematical calculation of the shadow prices and heuristic calculation, providing consistent results.
The paper is organized as follows: Sections 2 and 3 describe the stages of work followed and the main concept of the model. Section 4 formulates the mathematical model and Section 5 presents the sensitivity analysis of the proposed model.
2. Stages of Work
The first stage of this study involves the recording and the evaluation of the pricing data coming from the international market of leasing satellite capacity as well as their statistical processing. Some charging schemes have been proposed for broadband networks while this work involves real pricing data [12] . A decision making tool that maximizes the profits of a satellite operator, is implemented in the second stage. The goal of the proposed model is to enable the decision maker, to determine the best possible scenario for the satellite operator, which is the scenario with the larger amount of income.
The hypothesis that a satellite operator has different lease demands from different customers is made. Each customer wants to hire satellite capacity with a specified bandwidth, for a given lease period, which has an associated cost. The model output provides guidelines on the combination of customers that is the most profitable for the operator.
A scenario can be customized by entering the characteristics of the customers. These are:
 : the type of the requested service,
: the type of the requested service,
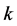 : the ascending number of customer
: the ascending number of customer 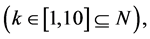
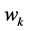 (MHz): the capacity in MHz that the
(MHz): the capacity in MHz that the 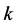 -th costumer requires
-th costumer requires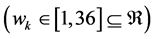 . If the required capacity is more than 36 MHz, then it can occupy one or more transponders completely. Therefore, for our calculations instead of
. If the required capacity is more than 36 MHz, then it can occupy one or more transponders completely. Therefore, for our calculations instead of 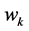 we compute
we compute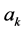 , which is the remaining capacity that does not occupy a whole transponder:
, which is the remaining capacity that does not occupy a whole transponder: 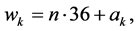
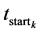 : the starting time (month) for which the k-th customer requires the leasing of capacity
: the starting time (month) for which the k-th customer requires the leasing of capacity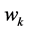 , considering a horizon of five years
, considering a horizon of five years ,
,
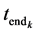 : the ending time (month) for which the k-th customer requires the leasing of capacity
: the ending time (month) for which the k-th customer requires the leasing of capacity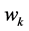 ,
, 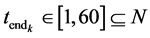 , and
, and
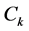 : the corresponding cost of lease, in Euros, for the k-th customer depending on the type of the requested service.
: the corresponding cost of lease, in Euros, for the k-th customer depending on the type of the requested service.
In the structure of the model, the possibility of beginning the hire in different time periods (different months) is included. Table 1 shows an example of the input parameters of the model.
The indicative cost for each service, is calculated using the data collected from the global satellite market. From the gathered data we created a basic classification of the possible services that a satellite operator could offer. These services correspond to different bandwidth demands and are presented in Table 2. The statistical analysis includes the pricing for the equivalent capacity, per 36 MHz, per month and the duration of lease in months. For each service, the mean value, the standard deviation, and the percentage of difference between standard deviation and mean value of these measures are determined along with their cross-correlation. Similar quantities are calculated for the duration of hire.
Table 1. Input parameters.
Table 2. Types of services.
3. Concept of the Model
The underlying concept of the problem of optimal allocation of the available satellite spectrum is based on a heuristic approach of the inventory control problem [7] . In the context of the proposed work, the model enables the comparison of 10 at most possible incoming customers with maximum required lease duration of 60 months, corresponding to a typical level of satellite demand. However, the model can easily be expanded to compare more customers requiring satellite capacity, for more than 5 years.
All the possible combinations of customers are calculated (see Figure 1 Group A), where a description of these combinations is given in terms of feasibility to implement or not. Specifically, there is an indication of Possible, Not Possible or Negotiable Combination for each combination of customers.
A Negotiable Combination is the combination of customers that exceeds by 1 MHz at most the highest possible capacity that a transponder can serve i.e. 36 MHz, which can probably constitute an issue of negotiation between the provider and the consumer. A Possible Combination is the feasible combination of customers from the point of view of the maximum capacity of the transponder and a Not Possible Combination is a not feasible one. The proposed tool gives the benefit of sorting by the Description of combination in order to present all the Possible Combinations (see Figure 1 Group B). The next step is to extract the Possible Combinations that are best to compare, by examining the most promising ones. This is done by selecting the combinations with the highest amount of total occupied capacity, which is the sum of the requested capacity by each customer of the combination (see Figure 1 Group C). Obviously, the more bandwidth is occupied from a transponder, the more profit there will be for the firm. These are the “Real Revenues”. This confines the search for the best case scenario to a small number of possible combinations.
The next step is to decide which of these combinations, with high occupied capacity, are more profitable. The criteria that are used to lead to the optimum combination are:
a) the amount of Real Revenues, representing the revenues that an operator will gain from hiring the capacity to the customers of each combination,
b) the calculation of Additional Expected Future Profits for the satellite operator, taking into consideration the standard deviation of the prices and consequently the corresponding risk.
Each combination has different time of maximum requested capacity hire. Therefore, in order to properly compare different scenarios, it is necessary to reduce them to the same time period i.e. to the same month of maximum hiring. We include to our calculations the additional possible income that can be acquired by this left over-free capacity that is called the “Remaining Capacity” (C Remaining). It is also possible that at specific months, not all the available capacity of the transponder of the satellite will be occupied with each combination. This leads to the undesirable effect of not having maximum occupancy of the transponder of the satellite, at each month. So the satellite operator could probably hire out this available capacity, to other possible future customers that are not included in the combination, and gain more revenues. This is called the “Empty Capacity” (C Empty). These moreover profits, consist the Additional Expected Future Profits.
Figure 1. Possible combinations of customers.
Let us examine the following example involving two cases that a satellite operator may need to compare and decide which one leads to maximum revenues. These are Scenario 1, which includes the combination of the customer number 1, 2, 3, 4 and 5 (Figure 2) and Scenario 2, which includes the combination of the customer number 6, 7, 8, 9 and 10 (Figure 3), with the characteristics shown in Table 1.
The sum of the occupied capacity of the transponder by the customers of the combinations in Scenario 1 and Scenario 2 are shown in Figure 4 and Figure 5, respectively. These figures represent the profile of the satellite transponder occupancy.
In Scenario 1, the maximum demand on the transponder’s capacity occurs during the 22nd month, while in Scenario 2, it occurs during the 30th month. The additional possible income that can be acquired from this left over free capacity is calculated. This is the “Remaining Capacity” (C Remaining) and appears at the white region in Figure 4.
Each Scenario does not lead to maximum occupancy of the transponder of the satellite at each month. This “Empty Capacity” (C Empty) is shown as the lined region of Figure 4 and Figure 5. For instance, in Scenario 1 (Figure 4) there are 21 MHz of unoccupied capacity during the 1st month, 20 MHz during the 2nd month, 5 MHz from the 3rd to the 5th month, 0 MHz between the 5th and the 10th month, etc. These expected profits are included to our calculations.
Figure 2. Scenario 1.
Figure 3. Scenario 2.
Figure 4. Scenario 3.
Figure 5. Scenario 4.
4. Structure of the Tool
Figure 6 shows the general structure of the model. This was implemented in Microsoft. NET environment in order to meet the need for increased computational burden. All feasible combinations of 




culations with only one customer, since this will not result to maximization of the profits for the operator.
The tool starts with the input as shown in Table 1, which is the demand of the customers that arrives to the satellite operator. Then all the combinations of customers are being calculated taking into account the evolution in time. The possible revenues for each scenario resulting from the leasing of the Remaining and the Empty Capacity are computed, using demand and pricing Parameters.
Figure 6. Structure of the tool.
4.1. Calculation of All Combinations of k Customers per k
All the possible combinations of the customers (PCf), 

where 

For our calculations we specify the following intermediate parameters:




We assign
4.2. Calculation of Revenues from C Empty
For each scenario the possible revenues from the future leasing of the “Empty Capacity” up to the 36 MHz, are calculated.
The Empty Capacity 

where 


This calculation is categorized depending on the amount of bandwidth that is not used each month by the customers of each combination. This “Empty Capacity” could potentially be hired out and generate revenues. The selected ranges of capacity in MHz are shown in Table 3, resulting from the gathered data.
We are considering 






to a capacity 


We use the notation:







The selected capacity ranges along with the corresponding probability of appearance of a new incoming customer, have been statistically computed by the available gathered data (Figure 7), and constitute the Parameter data set (Figure 6).
A decision tree arises for each scenario, as shown in Figure 8.
Figure 7. Pricing schemes (mean value price, standard deviation per MHz, per month, probability of appearance of a customer, in one month) for each range of Empty Capacity.
Figure 8. Revenues from C empty.
Table 3. Ranges of empty capacity.
The Expected Values of theoretical income, resulting from the “Empty Capacity” for each combination, depending on the not-leased bandwidth at each time period, are calculated as:

The standard deviation of the Expected Value, for each combination is:

The probable revenues for each combination, which are called Theoretical Revenues, depending on the number of MHz that are not used, are calculated as:

While the standard deviation of the Theoretical Revenues for each combination is:

The Expected Values of Revenues are calculated as intermediate volumes, which are used only for comparison purposes among scenarios. Such revenues incorporate the corresponding risk, and measure the monetary value of each scenario. The values of Theoretical Revenues are the real amounts of money (in Euros) that can be acquired, following each branch of the decision tree.
4.3. Calculation of Revenues from C Remaining
We proceed analogously calculating all possible revenues, (Expected Values and Theoretical Revenues) that can result from the leasing of the “Remaining Capacity”. This calculation is categorized depending on the type of service (s), using the statistically processed data (Figure 9), forming a decision tree (Figure 10 up).
First, we calculate the remaining time
maximum requested month of lease by the customers of the (PCf) combination, until the max requested time of all compared scenarios.

The following variables are introduced:


Figure 9. Pricing schemes (mean value price, standard deviation per 36 MHz, per month, probability of appearance of a customer, in one month) for each service.
Figure 10. Output of the model-decision tree.

These variables also constitute the Parameter data set and have been statistically calculated by the available gathered data.
The Expected Values of theoretical income for the Remaining Capacity depending on the type of service are:

The standard deviation of the Expected Value for each combination is:

While the Theoretical Revenues for the Remaining Capacity are:

and the standard deviation of the Theoretical Revenues for each combination is:

All the calculations concerning demand as well as the mean values of the prices of lease and standard deviations of prices are based on statistical computation of the real data coming from the international market and constitute the Parameter data set.
4.4. Output Function Formulation
All of these evaluated data are presented in the form of a unified decision tree (Figure 10), which is the output of the model.
The amount of Total Expected Revenues that will estimate the optimal policy for the firm is the sum of all revenues. This sum consists of the Real Revenues, plus the Expected Value resulting from the leasing of the Empty Capacity, plus the Expected Value resulting from the leasing of the Remaining Capacity, including their standard deviations, which are the Additional Expected Future Profits.
The Real Revenues are:

where 
the satellite operator, and belongs to the Input Parameters. An indicative cost, for each service, which applies to the international market, has been calculated by the gathered data. These values provide information to the incumbent operator for the current trends of satellite services billing and can be modified accordingly.
The Total Expected Revenues give a range of values, defining the best and worst case scenario for the revenues of the satellite operator.

where:

and

The real amount of money, resulting from each brand of the decision tree that will possibly result to the satellite operator is:

where:

and

This gives the opportunity to the satellite provider to determine which combination is the most profitable, for the present and in the future. The decision is made using the amount of Total Expected Revenues. This is not the real revenue that can be acquired, but it is an intermediate amount, which takes into account the corresponding probabilities, and is used for comparison purposes of the scenarios. The Total Expected Revenues is a decision quantity that incorporates profits and associated risk. This amount gives an estimate of the extent/worthness of the risk.
The decision making process starts from the identification of the highest Real Revenues, then the possible additional revenues are considered with their corresponding standard deviation that measures risk. This result to a
range of Total Expected Revenues with central value:


The final decision depends on the extent of risk that the firm is willing to take and on the particular policy that wants to apply. For a risk-loving decision maker the policy generating the highest Total Expected Revenues (upper limit) is chosen. A risk-neutral decision maker will take the policy with the central value, whereas for a risk-averse decision maker the policy generating the lowest of Total Expected Revenues (lower limit) will be chosen. The real amount of income that will result from each decision is the amount of Total Revenues of the corresponding scenario.
5. Sensitivity Analysis
Sensitivity analysis is necessary in validating the efficiency of a model. Due to the stochastic nature of the input parameters, we calculate the variance to the output of the model, caused by small variation of the input. The statistical processing of the pricing data gathered from the international market provided us with pricing and probability parameters. Since these variables may not be very accurate, we study the effect caused by small errors on their values.
These parameters include three categories:
pricing and demand (probability) data concerning the Remaining Capacity 
pricing and demand (probability) data concerning the Empty Capacity 
the Probability of a new incoming customer asking the Satellite provider for satellite services
The sensitivity analysis for these input parameters was performed by creating a small perturbation for each one of them. The value of each parameter was varied by ±2% and the corresponding change in the output, which is the Total Expected Revenues (TER), was measured. The analysis was performed in two different ways: first by theoretical calculation of the shadow prices of the input parameters and second using a heuristic technique, implemented by immediate application of the input-change to the model and observation of the output.
5.1. Mathematical Calculation
The shadow prices of the price parameters




parameter that we would like to examine.
The Sensitivity of the Total Expected Revenues with respect to the parameter 

The Sensitivity of the Total Expected Revenues with respect to the parameter 

We proceed calculating the Bode Sensitivity function for the demand parameters





ing probabilities parameter, expressing the variation 



The Sensitivity of the Total Expected Revenues with respect to the parameter 

The Sensitivity of the Total Expected Revenues with respect to the parameter 

The Sensitivity of the Total Expected Revenues with respect to the parameter 

All parameters ranges, involved in the calculation of the sensitivity analysis are presented in Table 4, resulting by the statistical analysis. Let us note that we consider a time period of 30 months allocated to the Remaining Capacity and 30 months allocated to the Empty Capacity. We calculated the summation of the Empty Capacity for each combination of customers
Table 5, summarizes the change to the output (minimum-maximum value) of the model caused by 2% change of the price and demand parameters considered. The analysis showed very small sensitivity to the demand parameter (probabilities



5.2. Heuristic Calculation
The Sensitivity analysis is now performed by immediate application of the variance of each input parameter, by ±2%, to the input of the model, and measuring of the output. A case study of six incoming customers, arriving to the satellite operator has been evaluated.
Two cases were considered. The best case scenario, which is the scenario generating the larger amount of expected revenues. This was identified by choosing for the calculations of the Remaining Capacity those that result from the Media Company Service, since it is the one with the highest pricing. The second case considered was the worst case scenario. This case accordingly resulted from the choice of Broadcast Service for the calculations of the expected revenues of the Remaining Capacity, which is the one with the lowest pricing. For each of these cases the calculations were extended to considering the upper limit and the lower limit of the Total Expected Revenues. A sensitivity analysis was performed for these 4 cases.
Using this small variation for each of the input parameters and for each case, we calculated 20 points of the output of the decision model, corresponding to different percentages of change of the input parameters between the ranges of ±2% of the central value.
For each change of input, the change of the output was calculated. This change has the form of the percentage of difference of the value of the output calculated for each of the 20 points of change to the input, minus the value of the output at the central point (11th point, with zero alteration), normalized to this central value.
Table 4. Parameters values ranges.
Table 5. Sensitivity analysis results.
The results of the sensitivity analysis for the best case scenario are shown in Figures 11-14. For each of the 20 different input sets we calculated the output on the four most profitable combinations of customers. Scenario1, is the scenario with the higher amount of Total Expected Revenues, Scenario 2 is the one with the second higher amount of Total Expected Revenues and so on.
Figure 11. Sensitivity analysis for Scenario 1.
Figure 12. Sensitivity analysis for Scenario 2.
Figure 13. Sensitivity analysis for Scenario 3.
Figure 14. Sensitivity analysis for Scenario 4.
In Scenario 2 (Figure 12), we observe a zero sensitivity of parameters



customers are zero.
The calculations were made for all 46 input parameters, categorized as shown in Table 4 and Table 5, extended to all of the 4 most profitable combinations, for both the best and worst case scenario. The most characteristic ones were presented. The results turned out to be similar.
The analysis showed very low sensitivity of the output to changes in the input parameters, even to the pricing parameters. The outcome using Heuristic calculations for the Sensitivity analysis were consistent with the outcome from the mathematical calculations. A small change to the pricing and to the demand parameters will not significantly change the output of the model. This is a very desirable feature, resulting from the good balancing of the proposed model. Even if the parameter data are not very accurate, the decision will not be greatly affected.
6. Conclusions
In this paper, we consider the techno-economic valuation of satellite services. The incremental growth of the satellite market nowadays, makes important the study of the economic feasibility of a satellite operator considering technological aspects of the application.
A dynamic mathematical model addressing the decision needs of an operator that provides satellite services is created. This decision making tool considers different demands of customers that arrive to the satellite operator.
Demand and pricing data have been gathered and statistically processed, from the international market. We present a model that compares different scenarios of combinations of customers with different demands, asking to hire satellite capacity. The model evaluates all probable revenues, along with their associated risks that could result from each decision branch. The tool incorporates all the valuable information that will help the satellite operator to determine the most profitable leasing scenario and allows alternative courses of enterprising steps depending on the company policy.
Sensitivity analysis has been included and showed a very small impact of the uncertainty of the input demand and pricing parameters to the final decision. This analysis could also be extended on simultaneous changes of several combinations of input parameters. This work addresses the real need of optimal satellite business planning. Other analysis was mainly referred to the economic evaluation to the physical layer of satellite planning.
The benefits of the model and of the analysis presented here for any satellite operator are clear. The same benefits may apply to related areas of activity where leasing of specific volumes to customers is the essence of the business enterprise.
Finally, we are currently extending our work, using the dynamic programming formulation, in discrete time and with stochastic elements.
Acknowledgements
This research has been co-financed by the European Union (European Social Fund—ESF) and Greek national funds through the Operational Program “Education and Lifelong Learning” of the National Strategic Reference Framework (NSRF)-Research Funding Program: THALES, Investing in knowledge society through the European Social Fund. The authors would also like to express their appreciation to Hellas Sat [13] , the Greek Satellite Operator, for their valuable support in data providing, developed tool usage and validation through business practice.
References
- Haase, E., Christensen, C.B. and Ten, C.H. (2012) Global Commercial Space Industry Indicators and Trends. Acta Astronautica, 50, 747-757. http://dx.doi.org/10.1016/S0094-5765(02)00005-X
- Marchese, M. and Jamalipour, A. (2005) Key Technologies and Applications of Present and Future Satellite Communications. IEEE Wireless Communications, 12, 8-9. http://dx.doi.org/10.1109/MWC.2005.1522097
- NSR (2010) Global Assessment of Satellite Supply & Demand. 8th Edition. http://www.nsr.com/research-reports/
- Wood, D. and Weigel, A. (2012) A Framework for Evaluating National Space Activity. Acta Astronautica, 73, 221- 236. http://dx.doi.org/10.1016/j.actaastro.2011.11.013
- Henri, Y. and Nozdrin, V. (2012) Economic Methods of Improving Efficient Use of the Orbit/Spectrum Resource by Satellite Systems. Space Policy, 28, 185-191. http://dx.doi.org/10.1016/j.spacepol.2012.07.001
- Saleh, J.H. and Padilla, J.P.T. (2007) Beyond Cost Models: Communications Satellite Revenue Models. Integrating Cost Considerations into a Value-Centric Mindset. International Journal of Satellite Communications and Networking, 25, 69-92. http://dx.doi.org/10.1002/sat.863
- Bertsekas, D.P. (2007) Dynamic Programming and Optimal Control. 3rd Edition, Athena Scientific, Belmont.
- Ross, S.M. (1983) Introduction to Stochastic Dynamic Programming. Academic Press, New York.
- Maral, G. and Bousquet, M. (1998) Satellite Communications Systems: Systems, Techniques and Technology. 3rd Edi- tion, John Wiley & Sons Ltd., New York.
- Sarri, E. (2007) Modelling and Techno-Economic Evaluation of Telecommunication—Satellite Services Using Optimization Techniques. Ph.D. Thesis, National Technical University of Athens, Athens.
- Pace, P. and Sun, Z. (2007) Demand Sensitive Model for Tuning Price over Satellite Digital Multimedia Broadcast System. IEEE Transactions on Broadcasting, 53, 329-337. http://dx.doi.org/10.1109/TBC.2006.889684
- Courcoubetis, C., Kelly, F.P., Siris, V.A. and Weber, R. (2000) A Study of Simple Usage-Based Charging Schemes for Broadband Networks. Telecommunications Systems, 15, 323-343.
- Sat, H. Greek Satellite Operator. http://www.hellas-sat.net

















