Open Journal of Optimization
Vol.3 No.2(2014), Article
ID:47192,6
pages
DOI:10.4236/ojop.2014.32002
The Neural Network That Can Find the Maximum Income of Refinery
Bahman Mashood1, Greg Milbank2
11250 La Playa Street. 304. San Francisco. CA 94109. USA
2Praxis Group. 1618 Northfield Road. Nanaimo. BC. V9S 3A9. Canada
Email: b_mashood@hotmail.com, Gregm@Praxistech.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 March 2014; revised 2 May 2014; accepted 4 June 2014
ABSTRACT
In this article we are going to introduce the neural network approach to approximate the solution for optimization problems. Using this approach we are able to approximate the optimum values for the large class of functions in particular give the prices of different products that are resulted from refining the crude petroleum into different substances. We are going to design a neural network that can provide us with a decomposition of the given crude petroleum into resulted products in such a ways that is most beneficial for the refinery.
Keywords:Neural Network, Optimization

1. Introduction
Many problems in the industry involved optimization of certain complicated function of several variables. Furthermore there are usually set of constrains to be satisfied. The complexity of the function and the given constrains make it almost impossible to use deterministic methods to solve the given optimization problem. Most often we have to approximate the solutions. The approximating methods are usually very diverse and particular for each case. Recet advances in theory of neural network are providing us with completely new approch. This approach is more comprehensive and can be applied to wide range of problems at the same time. In the preliminary section we are going to introduce the neural network methods that is based on the works of D. Hopfield, Cohen and Grossberg. One can see these results at (Section-4) [1] and (Section-14) [2] . We are going to use the above methods to find the maximum of the refinery under certain assumptions. Our calculations are based on the system of neural networks which is combined of four different neural networks will be utilized. It will provide us with the desired results that will be included in final section. The results in this article are based on our common work with Greg Milbank of praxis group. Many of our products used neural network of some sort. Our experiences show that by choosing appropriate initial data and weights we are able to approximate the stability points very fast and efficiently. In Section-3 we introduce the extension of Cohen and Grossberg theorem to larger class of differential equations. The appearance of new generation of super computers will give neural network much more vital role in the industry, machine intelligent and robotics. The references [1] -[4] can help the readers to get comprehensive ideas about neural networks, linear programming and matrices.
1.1. On the Structure and Application of Neural Networks
Neural networks are based on associative memory. We give a content to neural network and we get an address or identification back. Most of the classic neural networks have input nodes and output nodes. In other words every neural networks is associated with two integers 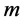 and
and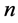 . Where the inputs are vectors in
. Where the inputs are vectors in  and outputs are vectors in
and outputs are vectors in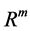 . neural networks can also consist of deterministic process like linear programming. They can consist of complicated combination of other neural networks. There are two kind of neural networks. Neural networks with learning abilities and neural networks without learning abilities. The simplest neural networks with learning abilities are perceptrons. A given perceptron with input vectors in
. neural networks can also consist of deterministic process like linear programming. They can consist of complicated combination of other neural networks. There are two kind of neural networks. Neural networks with learning abilities and neural networks without learning abilities. The simplest neural networks with learning abilities are perceptrons. A given perceptron with input vectors in 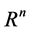 and output vectors in
and output vectors in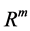 , is associated with treshhold vector
, is associated with treshhold vector 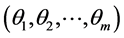 and
and 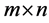 matrix
matrix![]() . The matrix
. The matrix ![]() is called matrix of synaptical values. It plays an important role as we will see. The relation between output vector
is called matrix of synaptical values. It plays an important role as we will see. The relation between output vector 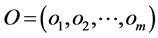 and input vector vector
and input vector vector 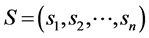 is given by
is given by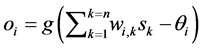 , with
, with ![]() a logistic function usually given as
a logistic function usually given as 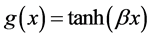 with
with 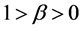 This neural network is trained using enough number of corresponding patterns until synaptical values stabilized. Then the perceptron is able to identify the unknown patterns in term of the patterns that have been used to train the neural network. For more details about this subject see for example (Section-5) [1] . The neural network called back propagation is an extended version of simple perceptron. It has similar structure as simple perceptron. But it has one or more layers of neurons called hidden layers. It has very powerful ability to recognize unknown patterns and has more learning capacities. The only problem with this neural network is that the synaptical values do not always converge. There are more advanced versions of back propagation neural network called recurrent neural network and temporal neural network. They have more diverse architect and can perform time series, games, forecasting and travelling salesman problem. For more information on this topic see (Section-6) [1] . Neural networks without learning mechanism are often used for optimizations. The results of D. Hopfield, Cohen and Grossberg, see (Section-14) [2] and (Section-4) [1] , on special kind of differential equations provide us with neural networks that can solve optimization problems. The input and out put to this neural networks are vectors in
This neural network is trained using enough number of corresponding patterns until synaptical values stabilized. Then the perceptron is able to identify the unknown patterns in term of the patterns that have been used to train the neural network. For more details about this subject see for example (Section-5) [1] . The neural network called back propagation is an extended version of simple perceptron. It has similar structure as simple perceptron. But it has one or more layers of neurons called hidden layers. It has very powerful ability to recognize unknown patterns and has more learning capacities. The only problem with this neural network is that the synaptical values do not always converge. There are more advanced versions of back propagation neural network called recurrent neural network and temporal neural network. They have more diverse architect and can perform time series, games, forecasting and travelling salesman problem. For more information on this topic see (Section-6) [1] . Neural networks without learning mechanism are often used for optimizations. The results of D. Hopfield, Cohen and Grossberg, see (Section-14) [2] and (Section-4) [1] , on special kind of differential equations provide us with neural networks that can solve optimization problems. The input and out put to this neural networks are vectors in 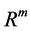 for some integer
for some integer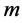 . The input vector will be chosen randomly . The action of neural network on some vector
. The input vector will be chosen randomly . The action of neural network on some vector  consist of inductive applications of some function
consist of inductive applications of some function 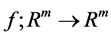 which provide us with infinite sequence
which provide us with infinite sequence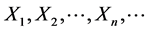 . where
. where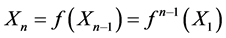 . And output (if exist) will be the limit of of the above sequence of vectors. These neural networks are resulted from digitizing the corresponding differential equation and as it is has been proven that the limiting point of the above sequence of vector coincide with the limiting point of the trajectory passing by
. And output (if exist) will be the limit of of the above sequence of vectors. These neural networks are resulted from digitizing the corresponding differential equation and as it is has been proven that the limiting point of the above sequence of vector coincide with the limiting point of the trajectory passing by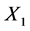 . Recent advances in theory of neural networks provide us with robots and comprehensive approach that can be applied to wide range of problems. At this end we can indicate some of the main differences between neural network and conventional algorithm. The back propagation neural networks, given the input will provide us the out put in no time. But the conventional algorithm has to do the same job over and over again. On the other hand in reality the algorithms driving the neural networks are quite massy and are never bug free. This means that the system can crash once given a new data. Hence the conventional methods will usually produce more precise outputs because they repeat the same process on the new data. Another defect of the neural networks is the fact that they are based on gradient descend method, but this method is slow at the time and often converge to the wrong vector. Recently other method called Kalman filter (see (Section-15.9) [2] ) which is more reliable and faster been suggested to replace the gradient descend method.
. Recent advances in theory of neural networks provide us with robots and comprehensive approach that can be applied to wide range of problems. At this end we can indicate some of the main differences between neural network and conventional algorithm. The back propagation neural networks, given the input will provide us the out put in no time. But the conventional algorithm has to do the same job over and over again. On the other hand in reality the algorithms driving the neural networks are quite massy and are never bug free. This means that the system can crash once given a new data. Hence the conventional methods will usually produce more precise outputs because they repeat the same process on the new data. Another defect of the neural networks is the fact that they are based on gradient descend method, but this method is slow at the time and often converge to the wrong vector. Recently other method called Kalman filter (see (Section-15.9) [2] ) which is more reliable and faster been suggested to replace the gradient descend method.
1.2. On the Nature of Crude oil and Its Decomposition
Crude oil is naturally occurring brown to black and is flammable liquid. It is principally found in oil reservoirs. Regardless of their origin all crude oils are mainly constituted of hydrocarbons mixed with variable amounts of sulfur nitrogen and oxygen compounds. The ratio of the different constituents in crude oil how ever vary appreciably from one reservoir to another. Crude oil are refined to separate the mixture into simpler fractions that can be used as a fuel, lubricates, or as intermediate stuck to petrochemical industries. The hydrocarbons in crude oil are mostly paraffines naphthenes and various aromatic hydrocarbons. The relative percentage of the hydrocarbons that appear in crude oil vary from oil to oil . In the average it is consistent of 30/100 paraffines, 40/100 naphthalene, 15/100 aromatic and 6/100 asphalt. The most marketable components of of petroleum are, natural gas, gasoline, benzine, diesel fuel, light heating oils, heavy heating oils and tars. The hydrocarbon components are separated from each other by various refinery process. In the process called fractional dissolution petroleum is heated and into a tower. The vapor of different components condense on collector at different heights in the tower. The separated fractions are then drown from the collectors and further processed into various petroleum products. As the light fractions specially gasoline are in high demand so called cracking procession have been developed in which heat and certain catalyst are used to break up the large molecules of heavy hydrocarbons into smaller molecules of lighter hydrocarbons. Some of the heavier fractions find eventual use as lubricating oil, paraffins, and medical substances. We can summarize the above decomposition methods in the following:
1) Fractional desolation: In this method which is used at the first stage, we use different levels of heat and pressure to desolate different products .
2) Chemical processing: In this method the given products are processed using chemical processing as in the the following. i) Each product can break down into smaller hydrocarbons. ii) Couple of smaller hydrocarbons will be combined to produce heavier hydrocarbons. Now given a market price for a Gallon of crude oil and expenses involved in producing a Gallon of each of the products we are going to introduce a method that can calculate the most beneficial decomposition of a given crude oil into resulted products. At this point we have to mention that the actual process of refining the crude oil might be much more complicated than a simplified version we use here. Our methods are based on some simple but sensible assumption about the process refinery. The a system of neural networks which is a combination of four neural networks will provide us with desired results. These neural networks are also able to extract some vital technical information about the process of refinery just by considering the given basic data.
1.3. Preliminary Model of the Problem in Finding the Maximum Income of Refinery
In this Section we are going to set some assumption regarding to the process of refining the crude oil and its decomposition. These assumption as we mentioned before are some how simplistic and will lead to the system of linear programming that will provide us with optimal solution. Since in reality the equations and constrains can be more complicated we introduce the algorithm based on theory of neural network. This algorithm can estimate the optimum for the cases where the functions and constrains are not linear. Suppose we are given a function 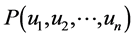 of
of 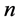 variables
variables 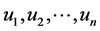 to be optimized. Furthermore for
to be optimized. Furthermore for![]() , let
, let![]() , to be the set of
, to be the set of  function. Assume we want to optimize the function
function. Assume we want to optimize the function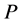 , given we have to satisfy the following constrains
, given we have to satisfy the following constrains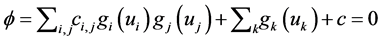 , where
, where 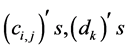 and
and ![]() are constants. Following the arguments at (Section-4) [1] and (Section-14.9) [2] we define energy function
are constants. Following the arguments at (Section-4) [1] and (Section-14.9) [2] we define energy function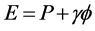 . Let us assume that
. Let us assume that 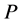 can be expressed as
can be expressed as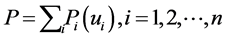 , where each
, where each 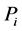 is a
is a ![]() function. Thus we have
function. Thus we have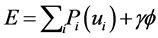 . Suppose
. Suppose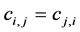 . and
. and  Now for
Now for  consider the following set of
consider the following set of 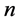 differential equations.
differential equations.![]() . Using the results of
. Using the results of
(Section 14.9) [2] , for each integer 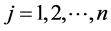 we get
we get 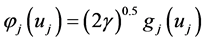 and
and
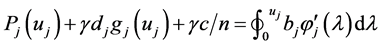 . Therefore we have,
. Therefore we have, . Finally the results of (Section-14-9) [2] , implies that as a function of time
. Finally the results of (Section-14-9) [2] , implies that as a function of time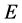 , is a decreasing function which guaranties that the above neural network will converges to optimum of
, is a decreasing function which guaranties that the above neural network will converges to optimum of 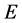 as the vector
as the vector 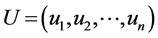 converge to the vector
converge to the vector![]() , as time goes to infinity. Let us by
, as time goes to infinity. Let us by ![]() the set of all optimization systems that we can find their optimum using the above process.suppose Given a polynomial
the set of all optimization systems that we can find their optimum using the above process.suppose Given a polynomial 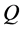 in
in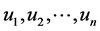 . Then using routine arguments in theory of functions of several variables we know that
. Then using routine arguments in theory of functions of several variables we know that 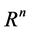 can be divided into the union of finite disjoint open sets. On each of this open sets the value of the function has the same sign. Next we define the function
can be divided into the union of finite disjoint open sets. On each of this open sets the value of the function has the same sign. Next we define the function 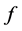 acting on
acting on 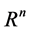 with
with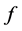 , equal to the absolute value of
, equal to the absolute value of . Thus
. Thus 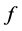 becomes a positive function on the domain
becomes a positive function on the domain 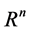 of
of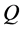 . Now given a system
. Now given a system 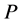 of differential equation
of differential equation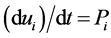 , with
, with 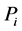 polynomial,suppose we can write that
polynomial,suppose we can write that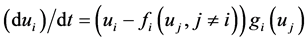 . Where all the functions in the i'th expression are polynomials of less degree than
. Where all the functions in the i'th expression are polynomials of less degree than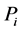 . Now let us define a simple energy function
. Now let us define a simple energy function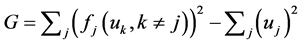 . By small variations around the boundary of
. By small variations around the boundary of 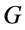 we can assume that
we can assume that 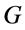 is
is ![]() function. Finally let us define the energy function
function. Finally let us define the energy function 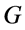 as in the following. There exist a sequence of disjoint open sets
as in the following. There exist a sequence of disjoint open sets 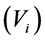 and a sequence of numbers
and a sequence of numbers 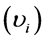 with
with ![]() takes one of the values 1 or −1. Then by making an appropriate choice for the above sets and integers
takes one of the values 1 or −1. Then by making an appropriate choice for the above sets and integers ![]() can be defined on each of the sets
can be defined on each of the sets ![]() to be equal to
to be equal to , such that the value of
, such that the value of![]() , will be strictly positive except at the critical point on which it vanishes. Furthermore
, will be strictly positive except at the critical point on which it vanishes. Furthermore  This implies that
This implies that ![]() is a Lyapunov function for the system
is a Lyapunov function for the system ![]() and the convergence to a critical point is asymptotically stable. Unfortunately the above arguments the existence of the critical points for the system.
and the convergence to a critical point is asymptotically stable. Unfortunately the above arguments the existence of the critical points for the system.
Theorem Suppose for each![]() ,
,  is a polynomial in term of its variables
is a polynomial in term of its variables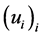 , satisfying the above conditions. Then
, satisfying the above conditions. Then 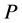 is in
is in![]() .
.
Let us pick up small compact subset 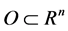 containing the the equilibrium point
containing the the equilibrium point![]() . Furthermore suppose the set of functions
. Furthermore suppose the set of functions 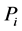 's are analytic functions. Then for any each
's are analytic functions. Then for any each ![]() small enough there exists an energy function
small enough there exists an energy function 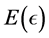 where
where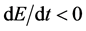 , as long as
, as long as 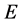 acts on
acts on ![]() minus the set of all elements that are
minus the set of all elements that are ![]() close to
close to![]() . This implies that if the set of functions involving the system
. This implies that if the set of functions involving the system 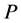 are analytic and if we can guess the region in which
are analytic and if we can guess the region in which ![]() is located then practically we can assume that
is located then practically we can assume that 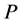 belong to
belong to![]() . This in fact need some extra initial work and assumptions about the polynomials involved in the above process of approximating the functions
. This in fact need some extra initial work and assumptions about the polynomials involved in the above process of approximating the functions 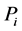 in the above differential equations. The problem with the above methods is how to pick the initial conditions in order not to end up in the local minima or local maxima. This will take some dedication. The experience shows that the best alternative is to choose the initial vector
in the above differential equations. The problem with the above methods is how to pick the initial conditions in order not to end up in the local minima or local maxima. This will take some dedication. The experience shows that the best alternative is to choose the initial vector 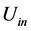 randomly and choose
randomly and choose ![]() to be of the same size as the average of
to be of the same size as the average of![]() ’s. Equally this can be done using generalized Hebb rule as given by the Formula (2.9) [1] . Now we introduce the set of neural networks that will approximate the solution to the refinery problem.
’s. Equally this can be done using generalized Hebb rule as given by the Formula (2.9) [1] . Now we introduce the set of neural networks that will approximate the solution to the refinery problem.
To begin with we assume the weight of the given crude oil is one gallon. Let us assume that , be the set of all hydrocarbons that can be extracted from crude oil. Let
, be the set of all hydrocarbons that can be extracted from crude oil. Let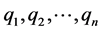 , be the corresponding percentage of them in one gallon of the given crude oil. During the refining process the product
, be the corresponding percentage of them in one gallon of the given crude oil. During the refining process the product![]() , will contribute
, will contribute 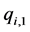 gallon of its weight to produce other substances . Conversely it receives
gallon of its weight to produce other substances . Conversely it receives 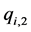 gallons as a result of chemical process between other products. The final amount of product
gallons as a result of chemical process between other products. The final amount of product![]() , at the end of refining process
, at the end of refining process![]() , will be given in the following
, will be given in the following
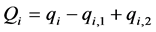 (1)
(1)
it makes sense to assume that for a given products ![]() and
and![]() , there exist coefficients
, there exist coefficients 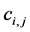 and
and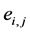 , such that the amount of contribution of product
, such that the amount of contribution of product ![]() to product
to product ![]() is equal to
is equal to 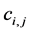 and the cost of this transformation is equal is equal to
and the cost of this transformation is equal is equal to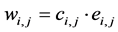 .
.
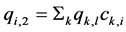 (2)
(2)
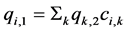 (3)
(3)
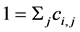 (4)
(4)
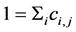 (5)
(5)
Suppose the price of one gallon of product ![]() is
is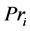 . This implies that the total profit
. This implies that the total profit 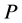 of the refinery is equal to the sum of the market price of resulted products minus the total expenses, i.e.,
of the refinery is equal to the sum of the market price of resulted products minus the total expenses, i.e.,
![]() (6)
(6)
And we wish to maximize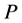 . Furthermore we have the following inequalities,
. Furthermore we have the following inequalities,
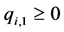 (7)
(7)
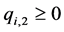 (8)
(8)
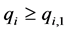 (9)
(9)
Assuming the values 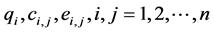 are known, the above system is the system of linear programming in term of
are known, the above system is the system of linear programming in term of ![]() variables
variables  and its solution will provide us with the maximal benefit. On the hand we might seek a brand of crude oil that can maximize the profit
and its solution will provide us with the maximal benefit. On the hand we might seek a brand of crude oil that can maximize the profit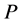 . In this case we use the fact that the maximum amount of product
. In this case we use the fact that the maximum amount of product ![]() that can be inside the gallon of crude oil is given to be less or equal than a given number
that can be inside the gallon of crude oil is given to be less or equal than a given number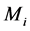 . In this case we have to add another set of
. In this case we have to add another set of  variables to the above system of linear programming and the following constrains:
variables to the above system of linear programming and the following constrains:
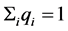 (10)
(10)
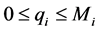 (11)
(11)
And the solution of this new system of linear progamming will identify the brand of crude oil that will bring maximum benefit. The problem is to find the coefficients  and
and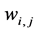 . In the proceeding Sections we will find ways to get away with this problem and also simplify the above system of linear programming in order to bring down the number of constrains.
. In the proceeding Sections we will find ways to get away with this problem and also simplify the above system of linear programming in order to bring down the number of constrains.
2. Connection to Perron Frobenius Theory
Let ![]() be
be 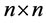 irreducible matrix with positive entries. The perron-frobenius theory states that the greatest eigenvalue
irreducible matrix with positive entries. The perron-frobenius theory states that the greatest eigenvalue ![]() of
of , is positive number. Further more it is a single root of the characteristic polynomial of
, is positive number. Further more it is a single root of the characteristic polynomial of 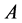 and has the largest absolute value among all other roots. Therefore the corresponding right eigenspace associated to
and has the largest absolute value among all other roots. Therefore the corresponding right eigenspace associated to ![]() is one dimensional. The same is true for the left eigenspace.Let
is one dimensional. The same is true for the left eigenspace.Let ![]() be the right eigenvector for
be the right eigenvector for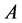 , (Respectively Let
, (Respectively Let ![]() be the left eigenvector for
be the left eigenvector for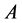 ), such that
), such that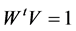 . Then it is well known that as
. Then it is well known that as ![]() tends to infinity,
tends to infinity,![]() . Now considering Equations (4) and (5) we can see that the matrix
. Now considering Equations (4) and (5) we can see that the matrix ![]() is stochastic matrix. Considering
is stochastic matrix. Considering ![]() as an operator then using the fact that all the entries of
as an operator then using the fact that all the entries of ![]() are all positive, then the adjoint operator
are all positive, then the adjoint operator 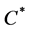 can be defined as
can be defined as ![]() Furthermore Equations (2) and (3) imply that the following equalities:
Furthermore Equations (2) and (3) imply that the following equalities:
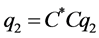 (12)
(12)
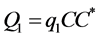 (13)
(13)
hold for each fixed![]() . But
. But 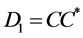 and
and 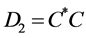 are self adjoint matrices which implies that for
are self adjoint matrices which implies that for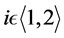 ,
, 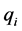 is an eigenvector for the matrix
is an eigenvector for the matrix ![]() corresponding to the eigenvalue equal to one. One the other hand the equalities (4) and (5), and the fact that the entries of
corresponding to the eigenvalue equal to one. One the other hand the equalities (4) and (5), and the fact that the entries of ![]() are all positive and less or equal than one, implies that the Perron Frobenius eigenvalue of
are all positive and less or equal than one, implies that the Perron Frobenius eigenvalue of ![]() is equal to one. Hence
is equal to one. Hence 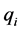 is a Perron Frobenius eigenvector for
is a Perron Frobenius eigenvector for![]() . Now summing the Equation (3) over the index
. Now summing the Equation (3) over the index ![]() then (12) and (13) imply the following equation
then (12) and (13) imply the following equation
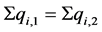 (14)
(14)
Let us set the following notations
 (15)
(15)
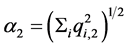 (16)
(16)
Then  and
and 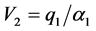 are standard Perron Frobenius eigenvectors for
are standard Perron Frobenius eigenvectors for ![]() and
and 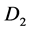 respectively. Now set
respectively. Now set ![]() and
and![]() . Then replacing
. Then replacing 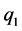 in (6) by
in (6) by![]() , we get,
, we get,
 (17)
(17)
Let us set the following notation,
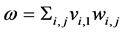 (18)
(18)
Then the Equation (17) can be written as in the following,
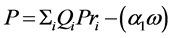 (19)
(19)
Let us define,
 (20)
(20)
Now by (1) and the above arguments we have,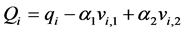 . Consider two fixed indices,
. Consider two fixed indices, 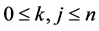 , such that
, such that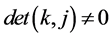 . Then the following equations,
. Then the following equations,
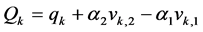
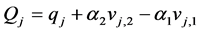
will provide us with values of ![]() and
and![]() .
.
Let us define, 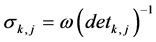 ,
, 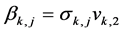 , and
, and 
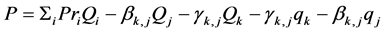 (21)
(21)
In order to maximize 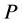 given by the Equation (21), we need to know the two values
given by the Equation (21), we need to know the two values  and
and![]() . This can be done by training a simple perceptron which we call neural network(A), with non-linear separability function, input data,
. This can be done by training a simple perceptron which we call neural network(A), with non-linear separability function, input data, 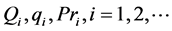 , output data
, output data 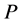 And weights that can be taken to be the values
And weights that can be taken to be the values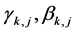 . As we can see at (Section-5) [3] , once we train the above perceptron with large enough set of contemporary data the corresponding weights will converge and give us the above values.Let us define the following vectors.
. As we can see at (Section-5) [3] , once we train the above perceptron with large enough set of contemporary data the corresponding weights will converge and give us the above values.Let us define the following vectors.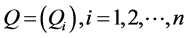 ,
, 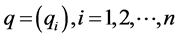 ,
, .
.
3. Final Conclusions
At this Section we formulate the final form of our neural network. Our neural network consists of four parts. At Part-I, we fixed two integers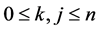 , such that
, such that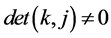 . Next using Neural network(A), which is based on simple perceptron we will calculate the values
. Next using Neural network(A), which is based on simple perceptron we will calculate the values ![]() and
and 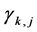 in term of large enough number of input vectors
in term of large enough number of input vectors 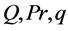 and output vector
and output vector 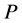 that would be used to train neural network(A). In Part-II, we use neural network(B) that is based on linear programming (20), calculating the variables
that would be used to train neural network(A). In Part-II, we use neural network(B) that is based on linear programming (20), calculating the variables 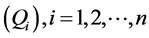 to maximize the profit
to maximize the profit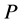 . The only constrains that are imposed on this neural network are the facts that the above variables are all positive and the following equation,
. The only constrains that are imposed on this neural network are the facts that the above variables are all positive and the following equation,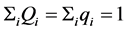 . At Part-III, neural network(C) will find the kind of crude oil that is the most beneficial for the refinery. Assuming that maximal percentage of the product
. At Part-III, neural network(C) will find the kind of crude oil that is the most beneficial for the refinery. Assuming that maximal percentage of the product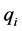 , inside the crude oil to be less or equal than the known number
, inside the crude oil to be less or equal than the known number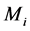 . It means that at this stage we have to add another
. It means that at this stage we have to add another 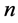 positive variables
positive variables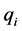 , satisfying the following set of constrains,
, satisfying the following set of constrains, 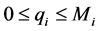 , to the linear programming (20). This new linear programming will provide us the values for the two vectors
, to the linear programming (20). This new linear programming will provide us the values for the two vectors 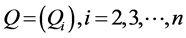 and
and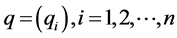 , and maximal value for
, and maximal value for 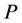 in term of
in term of 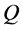 and
and![]() . Finally we can train neural network(D) that is based on back propagation. This neural net work is trained, using enough number of data which takes
. Finally we can train neural network(D) that is based on back propagation. This neural net work is trained, using enough number of data which takes ![]() and
and 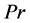 as an input with
as an input with  and
and 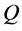 as an output. After the training is completed neural network(D) is able to give us
as an output. After the training is completed neural network(D) is able to give us 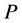 and
and 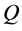 as soon as we plug in the vectors
as soon as we plug in the vectors ![]() and
and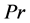 .
.
References
- Hetz, J., Krough, A., Hetz, R.P.J., Krough, A. and Palmer, R. (1991) Introduction to the Theory of Neural Computation. Copy Right C, Addison Wesley Company.
- Haykin, S. (1999) Neural Networks A Comprehensive Foundation. 2nd Edition, Prentice Hall. Inc.
- Gass, I. (1958) Linear Programming. McGraw Hill, New York.
- Minc, H. (1988) Nonnegative Matrices. John Wiley and Sons. New York.

