Open Journal of Optimization
Vol.1 No.2(2012), Article ID:26124,5 pages DOI:10.4236/ojop.2012.12003
Improved Conditions for the Existence and Uniqueness of Solutions to the General Equality Constrained Quadratic Programming Problem
1Department of Mathematics, University of Science and Technology of China, Hefei, China
2Department of Mathematics, Faculty of Pure and Applied Sciences, Fourah Bay College, University of Sierra Leone, Freetown, Sierra Leone
3Department of Mathematics, Harbin Institute of Technology, Harbin, China
4Department of Mathematics, Faculty of Education, Kassala University, Kassala, Sudan
Email: *amadu_fullah2005@yahoo.com, d2ydx@yahoo.com, mujahid@mail.ustc.edu.cn
Received October 21, 2012; revised November 24, 2012; accepted December 3, 2012
Keywords: Hessian Matrix; Global Solutions; Equality Constrained Quadratic Programming; Existence and Uniqueness of Solutions; Lagrangian Methods; Schur Complement Methods
ABSTRACT
This paper presents an approach that directly utilizes the Hessian matrix to investigate the existence and uniqueness of global solutions for the ECQP problem. The novel features of this proposed algorithm are its uniqueness and faster rate of convergence to the solution. The merit of this algorithm is base on cost, accuracy and number of operations.
1. Introduction
Usually the general quadratic programming 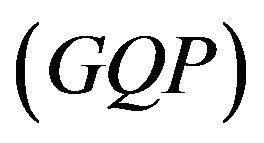 problem has a structure of the form
problem has a structure of the form
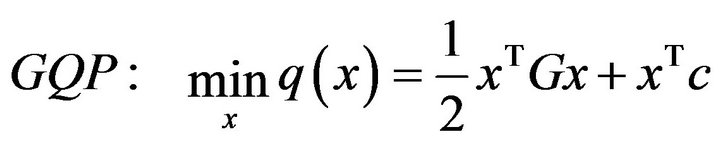
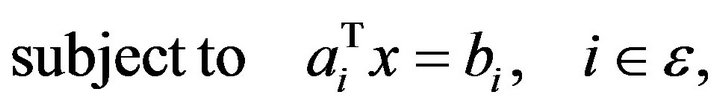

where 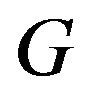 is a symmetric
is a symmetric ![]() matrix,
matrix, ![]() and
and  are finite sets of indices. In quadratic programming problems, the matrix
are finite sets of indices. In quadratic programming problems, the matrix 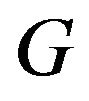 is called the Hessian matrix. The vectors
is called the Hessian matrix. The vectors 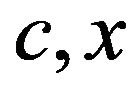 and
and 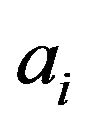 are column vectors in
are column vectors in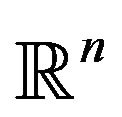 . To make computational life easier, we consider only the equality constraints and formulate the equality constrained quadratic programming
. To make computational life easier, we consider only the equality constraints and formulate the equality constrained quadratic programming 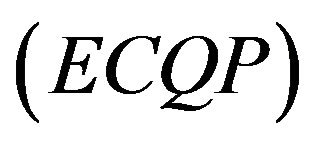 problem as follows
problem as follows
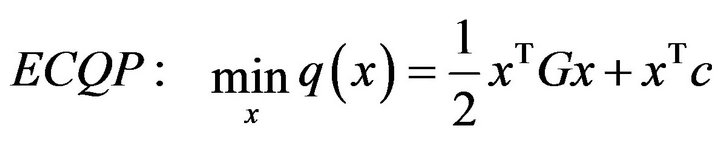
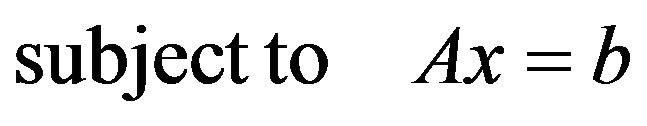
where  is a
is a ![]() jacobian matrix of constraints (with
jacobian matrix of constraints (with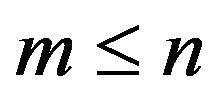 ) [1]. Throughout this paper, we will assume that
) [1]. Throughout this paper, we will assume that  can be of any form, since it is not a participant in the determination of the ECQP’s global minimum. Quadratic programming problems occur naturally, and sometimes stem as subproblems in general constrained optimization methods, such as sequential quadratic programming, augmented Lagrangian methods, and interior point methods. This type of programming problems occurs in almost every discipline and as a result became a topic of interest to a lot of researchers [1-3].
can be of any form, since it is not a participant in the determination of the ECQP’s global minimum. Quadratic programming problems occur naturally, and sometimes stem as subproblems in general constrained optimization methods, such as sequential quadratic programming, augmented Lagrangian methods, and interior point methods. This type of programming problems occurs in almost every discipline and as a result became a topic of interest to a lot of researchers [1-3].
In sequential quadratic programming 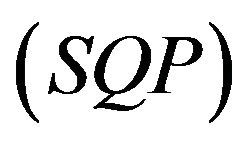 algorithms, an
algorithms, an 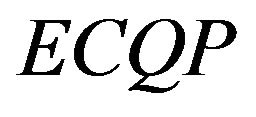 phase that employs second derivative information (Hessian matrix) is usually added to enhance rapid convergence to the solution [4-7]
phase that employs second derivative information (Hessian matrix) is usually added to enhance rapid convergence to the solution [4-7] 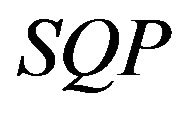 algorithms [8] that utilize the exact Hessian matrix are often preferred to those that use convex quasi-Newton approximations [9-11] since they need lesser time to converge to the solution.
algorithms [8] that utilize the exact Hessian matrix are often preferred to those that use convex quasi-Newton approximations [9-11] since they need lesser time to converge to the solution.
In 1985, Gould investigates the conditions under which the 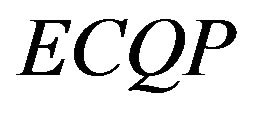 problem can be said to have a finite solution. Gould’s analysis of the
problem can be said to have a finite solution. Gould’s analysis of the  problem is based on the concepts of the reduced Hessian matrix
problem is based on the concepts of the reduced Hessian matrix 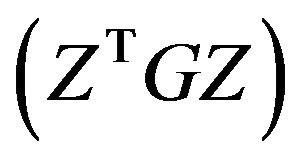 and signs of the eigenvalues of the Karush-Kuhn Tucker
and signs of the eigenvalues of the Karush-Kuhn Tucker  matrix [3]. The well known
matrix [3]. The well known  matrix has the form
matrix has the form
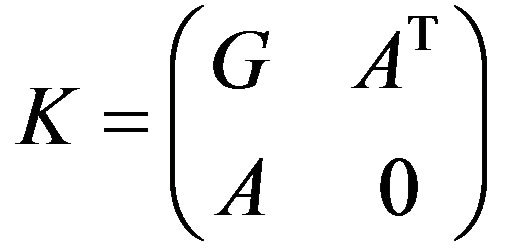
[1]. For small-scale  problems it is possible to solve the
problems it is possible to solve the 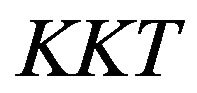 matrix (and hence, the
matrix (and hence, the 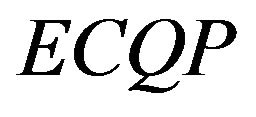 problem ) analytically [1,3,12]. The matrix
problem ) analytically [1,3,12]. The matrix  is one whose columns are a basis for the null space of
is one whose columns are a basis for the null space of  (matrix of contraints), and is obtained from the
(matrix of contraints), and is obtained from the  factorization of
factorization of . We investigated the method and found that the reduced Hessian matrix is not always accurate due to rounding off errors arising in the calculation of
. We investigated the method and found that the reduced Hessian matrix is not always accurate due to rounding off errors arising in the calculation of  [13-15].
[13-15].
Our goal in this paper is to present a new method that utilizes a necessary and sufficient condition for the existence and uniqueness of the solutions of the 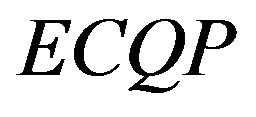 problem. In this paper, we show that for the
problem. In this paper, we show that for the 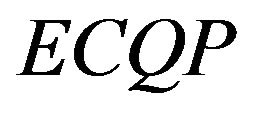 problem to have a global solution, its Hessian matrix must possess a Cholesky factor. As we shall see in Section 2, this paper focuses only on the condition(s) under which the
problem to have a global solution, its Hessian matrix must possess a Cholesky factor. As we shall see in Section 2, this paper focuses only on the condition(s) under which the 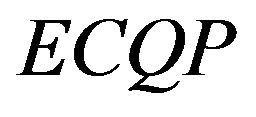 problem is said to have a global solution [16].
problem is said to have a global solution [16].
This paper is organized as follows. In Section 2, we discuss our method. Gould’s method is reviewed in Section 3. The analysis follow in Section 4 and some concluding remarks are made in Section 5.
2. Method
In this section, we introduce our new method of analyzing the solution of the 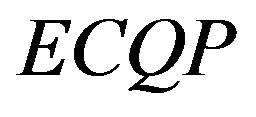 problem. It is based on the fact that the Cholesky decomposition is unique for positive definite matrices.
problem. It is based on the fact that the Cholesky decomposition is unique for positive definite matrices.
Cholesky Decomposition
Let  be a matrix that can undergo Cholesky decomposition with a Cholesky factor
be a matrix that can undergo Cholesky decomposition with a Cholesky factor ![]() (Lower triangular matrix) then we can write
(Lower triangular matrix) then we can write
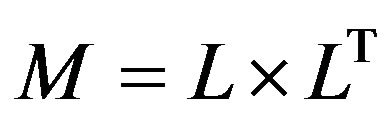 (2.1)
(2.1)
where 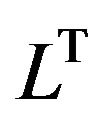 is the transpose of
is the transpose of![]() . We let
. We let
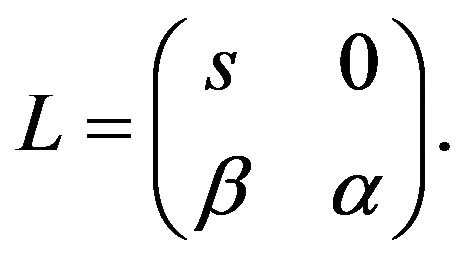 (2.2)
(2.2)
Substituting Equation (2.2) into Equation (2.1) gives
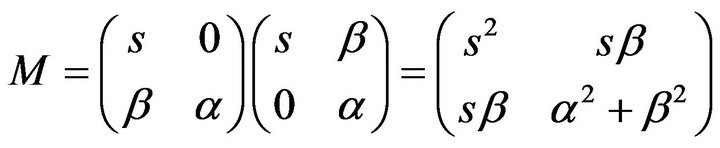 (2.3)
(2.3)
From Equation (2.3), we see that the conditions for 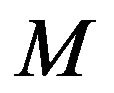 to be positive definite are satisfied. Therefore,our conditions for positive definiteness are; the matrix must be a square matrix and possesses a Cholesky factor.
to be positive definite are satisfied. Therefore,our conditions for positive definiteness are; the matrix must be a square matrix and possesses a Cholesky factor.
We let 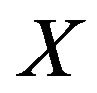 to be a
to be a ![]() column vector say
column vector say
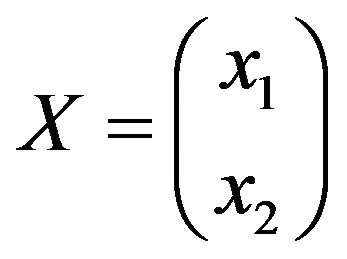 (2.4)
(2.4)
and we write
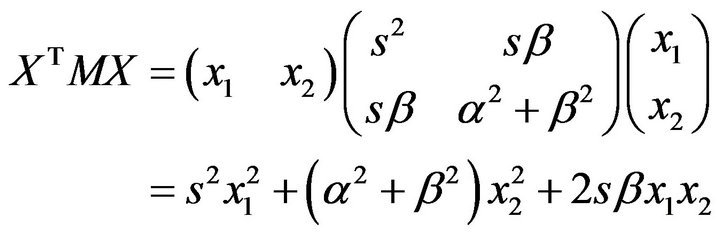 (2.5)
(2.5)
From Equation (2.3), it is clear that the first and second terms are always positive, which implies their sum is also always positive and greater than the third term if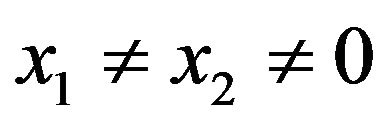 . When
. When 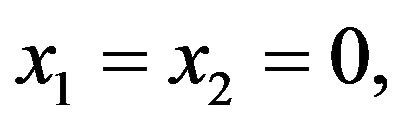 the matrix
the matrix 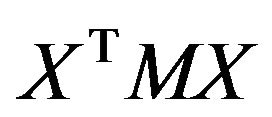 always equals zero. Therefore, the matrix
always equals zero. Therefore, the matrix 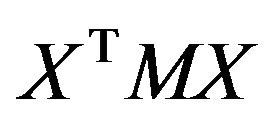 is always positive if and only if the column vector
is always positive if and only if the column vector 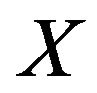 has entries
has entries 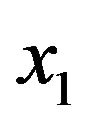 and
and 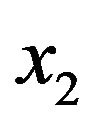 (such that
(such that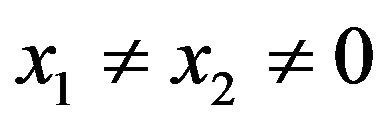 ) and the matrix
) and the matrix 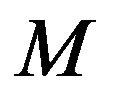 has a Cholesky factor.
has a Cholesky factor.
In the above demonstration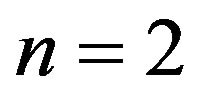 , which means that a
, which means that a 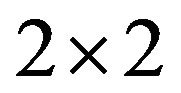 matrix
matrix 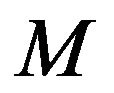 and a
and a ![]() column vector
column vector 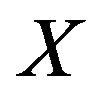 produces Equation (2.5). Analogously, any
produces Equation (2.5). Analogously, any ![]() matrix
matrix 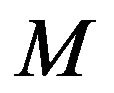 and any
and any ![]() column vector
column vector 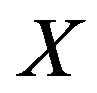 (where
(where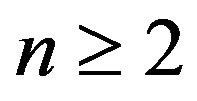 ) shall produce an equation similar in properties to Equation (2.5). If and only if
) shall produce an equation similar in properties to Equation (2.5). If and only if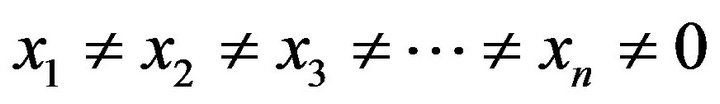 .
.
Corollary 2.1: Let  be any non-singular matrix and the Hessian matrix being Cholesky factorizable. Then the
be any non-singular matrix and the Hessian matrix being Cholesky factorizable. Then the 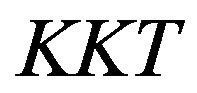 matrix
matrix
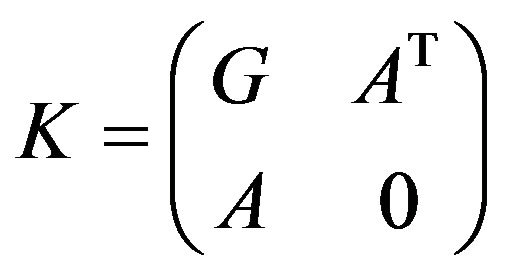 (2.6)
(2.6)
is nonsingular and has a unique solution.
Corollary 2.2: Let  be the Karush-Kuhn-Tucker matrix
be the Karush-Kuhn-Tucker matrix
 (2.7)
(2.7)
and assume  is any matrix. Then the
is any matrix. Then the  problem has a global minimum if and only if the Hessian matrix has a Cholesky factor.
problem has a global minimum if and only if the Hessian matrix has a Cholesky factor.
3. Review of Gould’s Method
In this section, we review Gould’s method. The method consists of three approaches: Null-space methods, Lagrangian methods and Schur complement methods [12].
Null-space methods: For  to be a solution of the
to be a solution of the 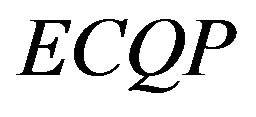 problem, a vector
problem, a vector 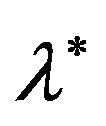 (i.e. Lagrange multipliers) must exist such that the system of equations below is satisfied
(i.e. Lagrange multipliers) must exist such that the system of equations below is satisfied
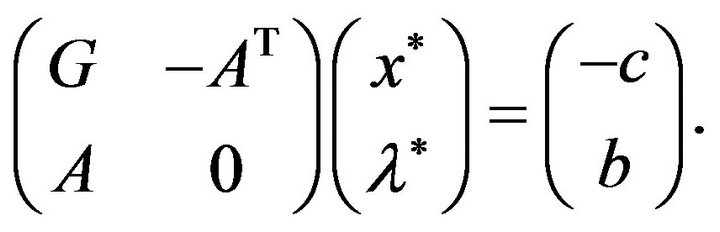 (3.1)
(3.1)
We let
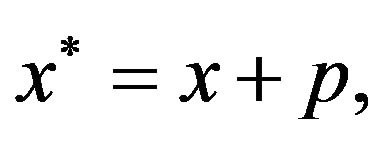 (3.2)
(3.2)
with ![]() being some estimate of the solution and
being some estimate of the solution and ![]() the desired step. By expressing
the desired step. By expressing 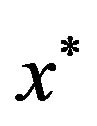 as in Equation (3.2), Equation (3.1) can be written in a form that is more useful for computational purposes as given below
as in Equation (3.2), Equation (3.1) can be written in a form that is more useful for computational purposes as given below
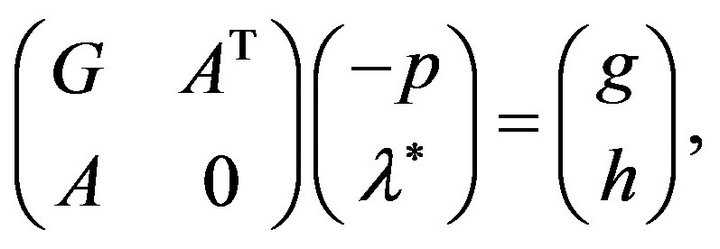 (3.3)
(3.3)
where
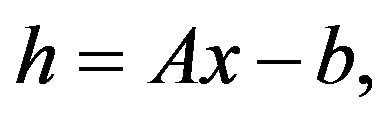 (3.4)
(3.4)
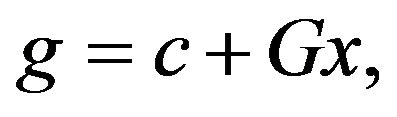 (3.5)
(3.5)
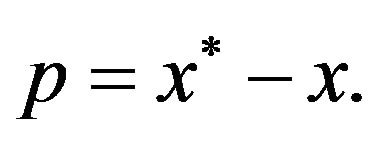 (3.6)
(3.6)
This method finds ![]() and
and 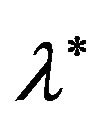 first, by partitioning the vector
first, by partitioning the vector ![]() into two components as follows
into two components as follows
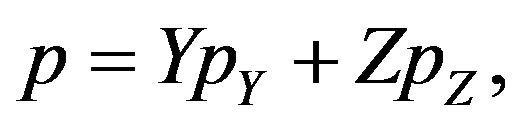 (3.7)
(3.7)
where ![]() and
and  have orthonormal columns and can be obtain from the
have orthonormal columns and can be obtain from the  factorization of
factorization of . An interesting property of this approach is that
. An interesting property of this approach is that 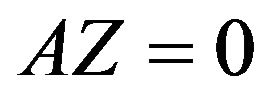 [1,3], which makes the calculation of
[1,3], which makes the calculation of ![]() and
and 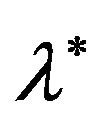 possible by solving the four equations below
possible by solving the four equations below
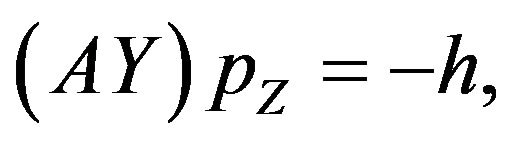 (3.8)
(3.8)
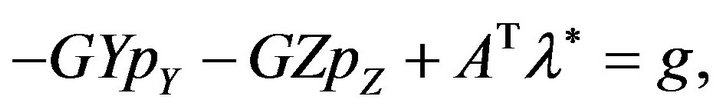 (3.9)
(3.9)
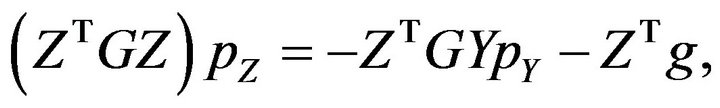 (3.10)
(3.10)
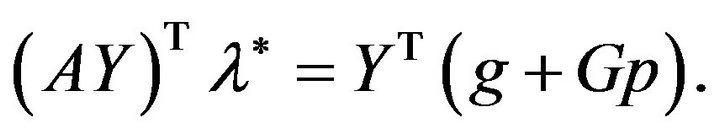 (3.11)
(3.11)
This method has a wider application than the Rangespace methods because; it doesn’t require 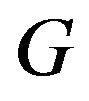 being nonsingular. According to this paper, the condition, that
being nonsingular. According to this paper, the condition, that 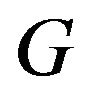 must undergo Cholesky decomposition is the only requirement for the
must undergo Cholesky decomposition is the only requirement for the  problem to have a global minimum. A knowledge of the null space basis matrix
problem to have a global minimum. A knowledge of the null space basis matrix  is not important at all.
is not important at all.
Lagrangian methods: This method calculates the values of ![]() and
and 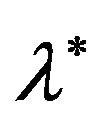 directly from Equation (3.3), i.e. the Karush-Kuhn-Tucker equations for the
directly from Equation (3.3), i.e. the Karush-Kuhn-Tucker equations for the 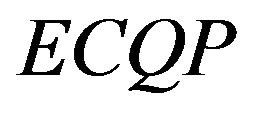 problem.
problem.
In this paper, the 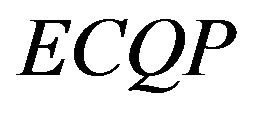 problem can only have a global minimum if
problem can only have a global minimum if 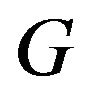 possesses a Cholesky factor
possesses a Cholesky factor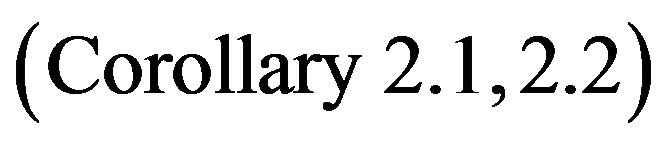 .
.
Schur complement methods: Here we assume that 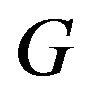 has a Cholesky factor and derive two equations from Equation (3.3) for the solutions of
has a Cholesky factor and derive two equations from Equation (3.3) for the solutions of ![]() and
and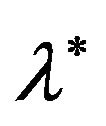 . These equations are as follows
. These equations are as follows
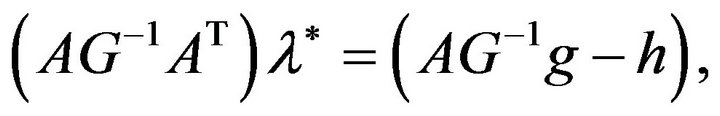 (3.12)
(3.12)
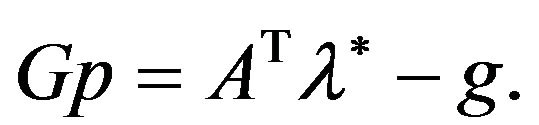 (3.13)
(3.13)
It is easy to see that both 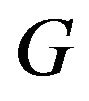 and
and 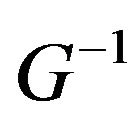 are positive definite. In this paper, we show that
are positive definite. In this paper, we show that 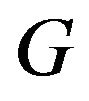 and
and 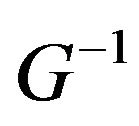 have Cholesky factors and hence
have Cholesky factors and hence 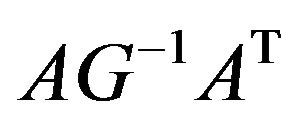 is always positive definite, which indicate the existence of a global solution for the
is always positive definite, which indicate the existence of a global solution for the 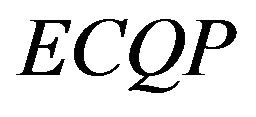 problem Section 2.
problem Section 2.
4. Analysis
In this section we will solve a numerical example from [1] using our algorithm and compared our results with those of Gould’s method. Let us consider the 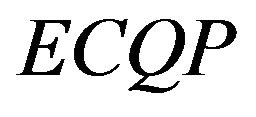 problem below and deduce whether it has a global minimum or not by using Gould’s method and our algorithm.
problem below and deduce whether it has a global minimum or not by using Gould’s method and our algorithm.
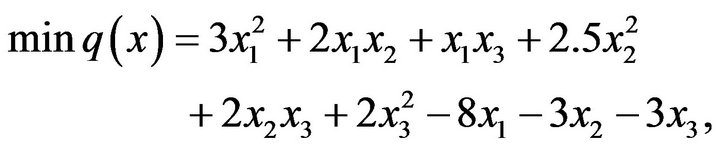
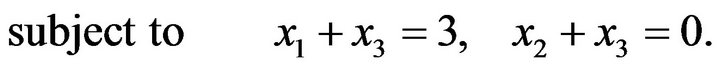 (4.1)
(4.1)
We will write the above  problem in the standard form described in the introduction by defining
problem in the standard form described in the introduction by defining
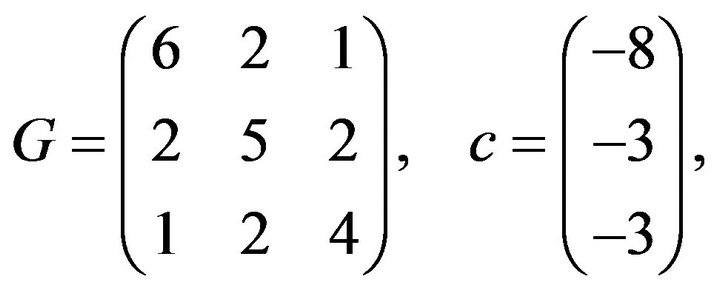
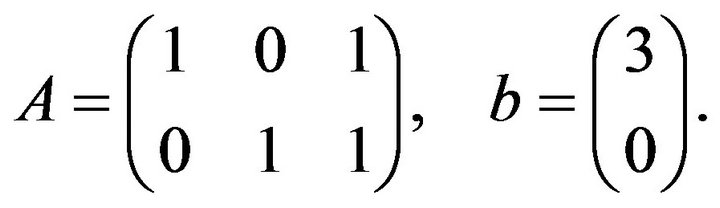
For Gould’s algorithm we need to find  from the
from the  factorization of matrix
factorization of matrix  i.e.
i.e.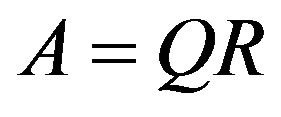 .
.


We can obtain  from the column space of matrix
from the column space of matrix  and the matrix
and the matrix  must satisfies the constrain
must satisfies the constrain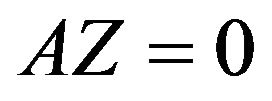 . Hence we have
. Hence we have
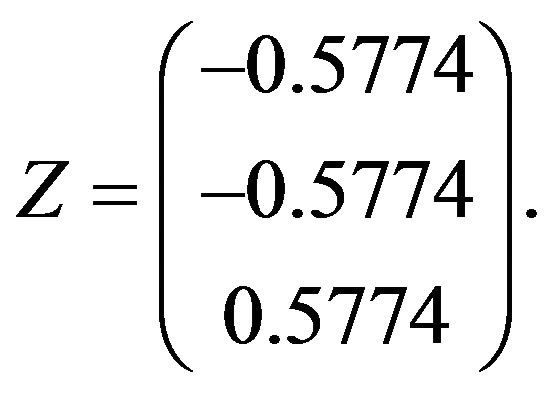
Therefore, 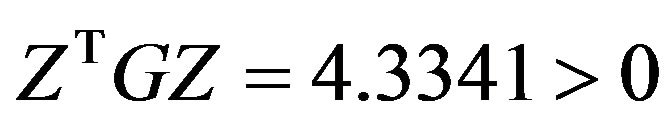 and according to Gould’s algorithm the
and according to Gould’s algorithm the 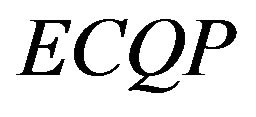 problem has a global minimum.
problem has a global minimum.
For our algorithm we only need to show that the matrix 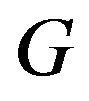 has a Cholesky factor. Let
has a Cholesky factor. Let ![]() be the Cholesky factor of
be the Cholesky factor of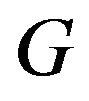 .
.

According to our algorithm,this implies the matrix 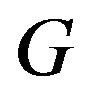 is positive definite and therefore the
is positive definite and therefore the 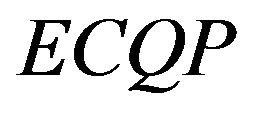 problem has a minimum solution. To show this fact we select any matrix that is a subset of the set of matrices described in subsection (2.1) and suppose we have that matrix to be
problem has a minimum solution. To show this fact we select any matrix that is a subset of the set of matrices described in subsection (2.1) and suppose we have that matrix to be
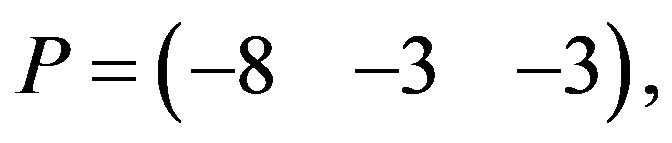 then
then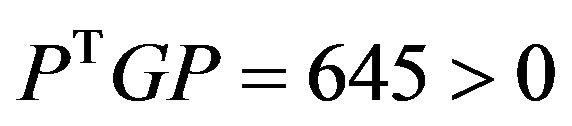 .
.
Let us consider another matrix
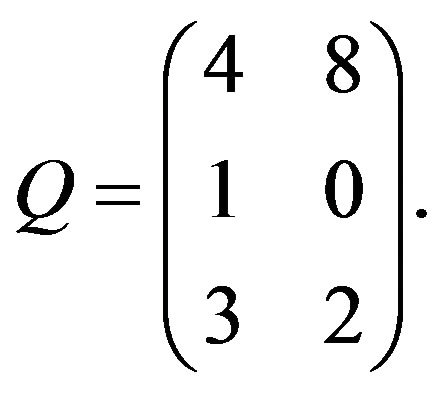
We will have result
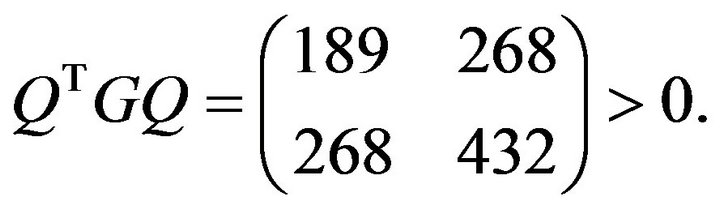
Finally, we consider a matrix with all negative entries as follows
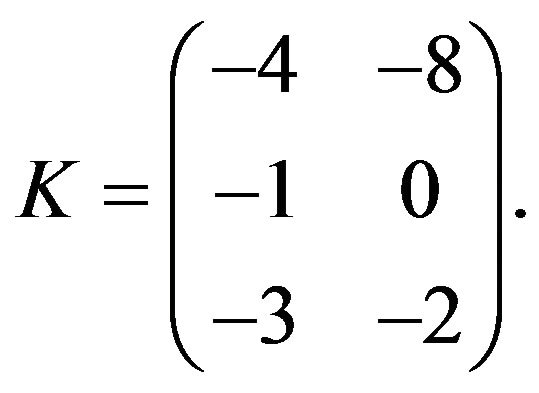
This gives the result
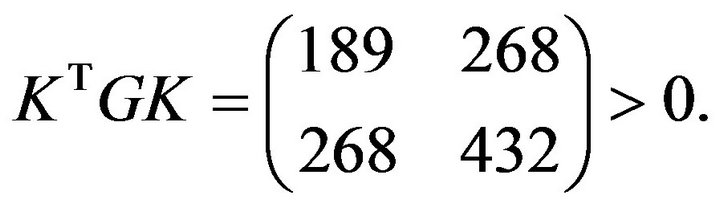
From the above example, we observed the following result:
1) Multiplying a matrix 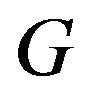 that has a Cholesky factor with any other matrix except the zero matrix, doesn’t alter the positive definite property of matrix
that has a Cholesky factor with any other matrix except the zero matrix, doesn’t alter the positive definite property of matrix 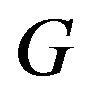 and hence the existence of global minimum.
and hence the existence of global minimum.
2) Decimals are encountered in Gould’s approach which may lead to rounding off errors and hence inaccuracy. Decimals have no effects on our method as long as the Hessian matrix has a Cholesky factor.
3) The number of matrix operations that are involved in Gould’s approach are far more than those that are involved in our algorithm which implies that our method is faster than that of Gould.
Gould’s approach uses the notion of the reduced Hessian matrix and the signs of the eigenvalues of the Karush-Kuhn-Tucker matrix to analyze the conditions under which the 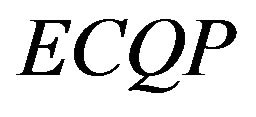 problem shall have a global solution [3]. It is clear that
problem shall have a global solution [3]. It is clear that 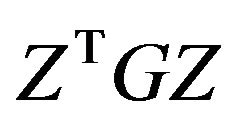 is sometimes incorrect due to rounding off errors in the calculation of
is sometimes incorrect due to rounding off errors in the calculation of . In this paper, we present a method that directly utilizes the Hessian matrix to analyze global minimum conditions for the
. In this paper, we present a method that directly utilizes the Hessian matrix to analyze global minimum conditions for the 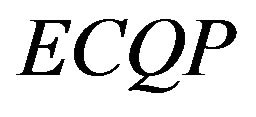 problem.
problem.
Finally, this proposed method has fewer iterations than Gould’s algorithm, inexpensive and naturally faster (Cholesky factorization) than Gould’s approach (with more iterations).
5. Conclusions
In 1985, Gould investigates the practical conditions for the existence and uniqueness of solutions of the 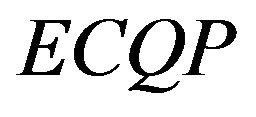 problem based on
problem based on 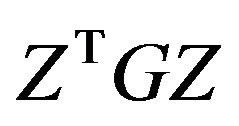 and inertia of the
and inertia of the 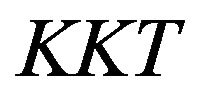 matrix. In this piece of work, we present a new method that directly works with
matrix. In this piece of work, we present a new method that directly works with 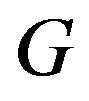 to analyze global solutions of the
to analyze global solutions of the 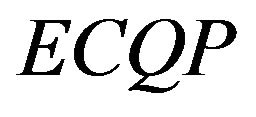 problem.
problem.
The advantages of our method lie in its accuracy, cost and number of operations. It is true that this noble algorithm is unique and computationally faster (i.e. Cholesky decomposition) than Gould’s method. Our method also revealed that if the Hessian matrix has a Cholesky factor then, the Hadamard inequality [17] for positive definiteness is satisfied as well.
We finally conclude that the existence and uniqueness of solutions of the 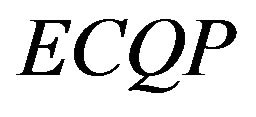 problem is independent of its constraints but depend wholly and solely on the Hessian matrix
problem is independent of its constraints but depend wholly and solely on the Hessian matrix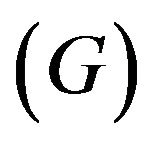 .
.
6. Acknowledgements
We would like to thank Khalid O. Elaalim for his useful contributions during the early stages of this work. We are also grateful to anonymous referees for their valuable comments on this paper. Finally, we would like to extend special thanks to the Chinese Scholarship Council which funded this research.
REFERENCES
- J. Nocedal and S. J. Wright, “Numerical Optimization,” 2nd Edition, Springer Series in Operations Research and Financial Engineering, Springer, New York, 2006, pp. 448-492. doi:10.1007/978-0-387-40065-5_16
- N. I. M. Gould, M. E. Hribar and J. Nocedal, “On the Solution of Equality Constrained Quadratic Programming Problems Arising in Optimization,” SIAM Journal on Scientific Computing, Vol. 23, No. 4, 2001, pp. 1376-1395. doi:10.1137/S1064827598345667
- N. I. M. Gould, “On Practical Conditions for the Existence and Uniqueness of Solutions to the General Equality Quadratic Programming Problem,” Mathematical Programming, Vol. 32, No. 1, 1985, pp. 90-99. doi:10.1007/BF01585660
- R. H. Byrd, N. I. M. Gould, J. Nocedal and R. A. Waltz, “An Algorithm for Nonlinear Optimization Using Linear Programming and Equality Constrained Subproblems,” Mathematical Programming, Vol. 100, No. 1, 2004, pp. 27-48.
- N. I. M. Gould and D. P. Robinson, “A Second Derivative SQP Method: Global Convergence,” SIAM Journal on Optimization, Vol. 20, No. 4, 2010, pp. 2023-2048. doi:10.1137/080744542
- N. I. M. Gould and D. P. Robinson, “A Second Derivative SQP Method: Local Convergence and Practical Issues,” SIAM Journal on Optimization, Vol. 20, 2010, pp. 2049-2079. doi:10.1137/080744554
- J. L. Morales, J. Nocedal and Y. Wu, “A Sequential Quadratic Programming Algorithm with an Additional Equality Constrained Phase,” IMA Journal of Numerical Analysis, Vol. 32, No. 2, 2012, pp. 553-579. doi:10.1093/imanum/drq037
- R. Fletcher and S. Leyffer, “Nonlinear Programming without a Penalty Function,” Mathematical Programming, Vol. 91, No. 2, 2002, pp. 239-269. doi:10.1007/s101070100244
- A. Drud, “CONOPT: A GRG Code for Large Sparse Dynamic Nonlinear Optimization Problems,” Mathematical Programming, Vol. 31, No. 2, 1985, pp. 153-191. doi:10.1007/BF02591747
- P. E. Gill, W. Murray and M. A. Saunders, “SNOPT: An SQP Algorithm for Large-Scale Constrained Optimization,” SIAM Journal on Optimization, Vol. 12, No. 4, 2002, pp. 979-1006. doi:10.1137/S1052623499350013
- K. Schittkowski, “The Nonlinear Programming Method of Wilson, Han and Powell with an Augmented Lagrangian Type Line Search Function,” Numerische Mathematik, Vol. 38, No. 1, 1981, pp. 83-114. doi:10.1007/BF01395810
- S. Boyd and L. Vandenberghe, “Convex Optimization,” Cambridge University Press, Cambridge, 2004, pp. 241- 245.
- E. Anderson, Z. Bai and J. Dongarra, “Generalized QR Factorization and Its Application,” Linear Algebra and Its Applications, Vol. 162-164, 1992, pp. 243-271. doi:10.1016/0024-3795(92)90379-O
- P. E. Gill and W. Murray, “Numerically Stable Methods for Quadratic Programming,” Mathematical Programming, Vol. 14, No. 1, 1978, pp. 349-372. doi:10.1007/BF01588976
- M. OCW, “Positive Definite Matrices and Minima,” 2012. http://ocw.mit.edu/courses/mathematics/18-06sc-linear-algebra-fall-2011/positive-definite-matrices-and -applications/postive-definite-matrices-and-minima/MIT18_06SCF11_Ses3.3prob.pdf
- Wikipidia, “Positive-Definite Matrix,” 2012. http://en.wikipedia.org/wiki/Positive-definite_matrix
- R. A. Horn and C. R. Johnson, “Matrix Analysis,” Cambridge University Press, Cambridge, 1985.
NOTES
*Corresponding author.

