Journal of Minerals and Materials Characterization and Engineering
Vol.04 No.04(2016), Article ID:68097,19 pages
10.4236/jmmce.2016.44023
The Effects of Frothers and Particles on the Characteristics of Pulp and Froth Properties in Flotation―A Critical Review
Wei Zhang1,2
1Mine Management Division, Department of Mining & Mineral Resources, Chinalco China Copper Corporation Limited, Beijing, China
2Department of Mining and Materials Engineering, McGill University, Montreal, Canada

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 May 2016; accepted 5 July 2016; published 8 July 2016
ABSTRACT
The pulp and froth zones are the main components of froth flotation as it defines both quality of the end product and overall efficiency. The importance of the properties of the two zones, which include pulp hydrodynamics, froth bubble coalescence rate, water overflow rate, air recovery, etc., is being increasingly recognized. The properties are depending not only on the type and concentration of the frother but also on the nature and amount of the particles present in the flotation system, and as well as the frother-particle interactions and potentially of bubble-particle interactions. To date, there is no specific criterion to quantify pulp and froth properties through the interactions between frothers and particles because the various related mechanisms occurring in the pulp and froth are not fully understood. Linking the properties to the metallurgical performance is also challenged. In order to better understand the effect of these issues in flotation, in this review paper, the past and recently published articles relevant to characterizations of pulp and froth properties are widely reviewed; the findings and the gap of knowledge in this area are highlighted for further research.
Keywords:
Flotation, Frothers, Bubble Surface Area Flux, Bubble Coalescence, Gas Holdup, Hydrophobicity

1. Introduction
In froth flotation, valuable mineral particles are separated from gangue minerals by exploiting differences in the hydrophobicity of the minerals. To effect separation, the surface properties of the selected (usually the valuable) mineral particles have to be controlled. To achieve this control a collector, a chemical surfactant, is added to increase the hydrophobicity of the target mineral surface while the gangue particles remain hydrophilic. Air is introduced into the flotation cell to generate bubbles together with another chemical surfactant, frother, added to help reduce bubble size and promote froth stability. The hydrophobic particles collide with and attach to the air bubbles, and are transported as a bubble-particle aggregate from the suspension (i.e., pulp zone) to the froth zone by buoyancy. The froth overflow product is typically the concentrate (i.e., the valuable mineral product). Meanwhile hydrophilic particles do not attach to the bubbles, and exit the cell as the tailing stream. Conceptually, flotation systems may be viewed as consisting of two zones: pulp and froth. The pulp zone is characterized by gas hold-up ca. 5% - 25% with regions of turbulence designed to promote bubble particle interaction. The froth zone is characterized by high gas hold-up (typ. 85% - 95% vol) and a relatively quiescent regime of upward moving and coalescing bubbles laden with hydrophobic particles, and downward flowing (draining) liquid carrying mis-placed (entrained) gangue particles. The presence of solids on the bubbles serves to stabilize the froth. Since flotation is a surface area (of gas) driven process, the size and behavior of bubbles in both pulp and froth phases are of paramount significance. In addition, according to the penetration theory proposed by Leja and Schulman [1] , frother molecules at the gas/liquid interface interact with collector molecules adsorbed on mineral particles.
It is evident, therefore, that the efficiency of flotation will depend on the use of frother to control bubble size, and hence particle collection in the pulp, and to stabilize the bubbles in order to exit the froth zone [2] - [4] . The use of frothers helps overall flotation performance by impacting both the quality (the grade) and quantity (the recovery) of the particles delivered to the concentrate [5] . The difficulty of interpreting frother functions in a 3- phase system (liquid-gas-solid) has been recognized [5] . There are several possible reasons: particles properties ranging from shape, size and degree of hydrophobicity affect froth stabilization; particles may interact with frothers (e.g. adsorb frother) thus changing both pulp and froth zone properties. A prime objective of this review paper is to explore how frothers and particles interact to affect the sub-processes occurring in the pulp and froth zones in order to better understand the effect of these issues in mineral flotation.
Compared to the well-studied 2-phase (gas-liquid) system, there is little literature on the 3-phase flotation system. In reality these systems can be considered to involve four phases: liquid, gas, hydrophilic solids and hydrophobic solids. Attached hydrophobic particles change the surface stress at the gas/liquid interface; and hydrophilic particles can modify the rheology of the interstitial fluid (the Plateau borders) within the froth [6] . Nevertheless it is important to understand the air-water system before including the addition of solids. The approaches include use of “ideal” particles, i.e., ones with well-defined properties tested in the laboratory and “real” particles tested in plant flotation conditions. Both approaches will be examined in this article.
2. Flotation Characterizations: Pulp and Froth
2.1. The Pulp Zone
The effect of solids in the pulp zone will be determined from measurements of bubble size distribution and gas hold-up. There is little literature on either relevant to flotation systems and that is contradictory. For instance, measurement of bubble size (Db) in a lab-scale cell by Grau et al. [7] suggested particles (hydrophilic quartz) cause an increase in Db. Finch et al. [8] inferring from data on sulphide flotation plants concluded particles had little effect, a finding apparent in the visualizations provided Quinn et al. [9] in laboratory column flotation tests on a sulphide ore. Kuan and Finch [10] concluded the presence of solids has little effect provided there is no adsorption of frother by the solid: in the case of talc and a polypropylene frother adsorption was sufficient to eliminate bubble size reduction but this was not the case with talc and alcohol frothers.
The general gas hold-up/gas velocity (Eg-Jg) relationship reflects solution chemistry (e.g. frother concentration) and slurry properties (e.g. percent solids), as illustrated in Figure 1. The relationship found in flotation cells is almost linear over the practical range of Jg [11] [12] . In 2-phase systems increasing frother concentration increases the gas holdup, Eg, reflecting since the impact of frother on reducing bubble size and, consequently, reducing bubble terminal velocity that means the gas residence time is increased [13] . The general observation on adding solids is to decrease Eg [14] . The usual explanation is that solids induce coalescence and the larger bubbles move faster. The tested systems often do not contain surfactant such as frother designed to retard coalescence. Banisi et al. [15] testing a range of solids in the presence of frothers presented data that suggested a de-
Figure 1. General trend in gas holdup upon increasing the (a) frother concentration only, and (b) percent solids only (adopted by [8] )
crease in gas hold-up can occur without change (increase) in bubble size. They argued that solids increased rise bubble rise velocity and this was the origin of the gas hold-up decrease. Flotation implies that particles are carried by bubbles and this can affect gas hold-up without changing bubble size. Garibay et al. [16] tested the impact of increasing solids content (%solids) in a flotation column where gas hold-up tends to increase up the column reflecting the increase in bubble size (volume) as static head pressure decreases. (The larger volume means higher local gas content, i.e., gas hold-up, and this is more significant than any increase in rise velocity due to increased bubble size and buoyancy [17] . They showed that above ca. 20% solids the gas holdup started to decrease with height now reflecting the slowing down of the bubbles due to the particle load. No independent measure of bubble was made to support the interpretation, however. Kuan and Finch [10] made a similar argument for the increase in gas hold-up in the case of talc and 1-pentanol noting that bubbles in this alcohol are not at terminal velocity and attached solids can slow the bubble rise. In that case it was confirmed by direct measurement that bubble size had not changed. Measurements of both bubble size and gas hold-up make for a powerful combination to interpret observations on the role of solids.
2.2. The Froth Zone
The froth zone has attracted increasing attention in the last decade [18] [19] including the role of solids as summarized in a recent review by Hunter et al., [20] . Froth is an integral part of the flotation system but despite the importance, relatively few studies have been conducted to examine the impact of froth variables (e.g. bubble size, frother type and concentration, liquid/gas/solid content) on the performance of flotation cells [21] - [25] . If the froth phase is not sufficiently stable (i.e., there is excessive bubble coalescence), mineralized bubbles that enter the froth may rupture prematurely causing valuable mineral particles to drop back into the pulp zone. Conversely, too stable froth may cause nonselective entrainment of hydrophilic gangue particles due to excessive water recovery, thereby reducing concentrate grade. Froth stability has been characterized by several methods including: water overflow rate [26] , gas retention time vs. frother concentration [27] , and froth height vs. gas holdup relationship [28] . Much of the work has focused on 2-phase systems. Moyo et al. [26] indicated the strong relationship between water overflow rate (i.e., JwO) and Eg in 2-phase tests and showed a unique relationship for each frother type. The presence of solids will influence JwO. The studies by Melo and Laskowski [29] and Kuan and Finch [10] comparing frother types showed that polyglycol frothers produced a higher JwO than alcohol frothers but that this order reversed in the presence of solids (naturally hydrophobic coal and talc, respectively). As noted in discussion of pulp zone properties the reason appears to be adsorption of some frothers by some solids and thus a change in froth zone stability. It is clear that froth stability is dependent not only on the type and concentration of frothers but also on the solids characteristics (concentration, degree of hydrophobicity, interaction with frother) [10] [20] [25] [30] - [32] . One way to study solids effects on pulp and froth zone properties while free of interaction with frother may be to use salts to replace frothers [33] .
3. Effect of Frothers on Flotation Sub-Processes
Frothers are non-ionic surfactants, commonly classified as alcohols and polyglycols, used in flotation [3] [34] . Alcohol types are generally considered as “weak” frothers having low surface activity (i.e., do not reduce surface tension much). Their frothing action increases with increasing chain length, with maximum occurring around six to seven carbon atoms. Alcohol frothers produce froths that are relatively shallow and “dry” (i.e. carry less water) [35] and have low persistence [36] . MIBC (methyl isobutyl carbinol) is the best-known frother in this group. Polyglycol type frothers form a large class with varying molecular structure and molecular weight. These frothers tend to produce relatively deep and “wet” froth, and hence more stable and persistent froths [36] . Flottec 150 (F150) and Dowfroth 250 (DF250) are among the best-known examples in this group.
3.1. In the Pulp
The concentration of frother in the pulp determines the extent of bubble coalescence [37] - [39] . The continued addition of frother has a diminishing effect resulting in bubble size reaching a limiting value at a concentration now referred to as the critical coalescence concentration (CCC) [39] . Although the mechanism by which frothers retard coalescence is still debated, evidence [7] [40] suggests that they might bind water molecules to the bubble surface by hydrogen bonding, thus making it more difficult for the water to drain between approaching bubbles. This phenomenon can be considered the origin of a surface viscosity that is different (higher) than the bulk [41] . Other researchers [34] [42] infer this mechanism also by reference to bubble hydration by frothers.
To help explain this mechanism, consider that frother molecules adsorb on the bubble surface with the hydrophilic (i.e., polar) group oriented to the water-side of the interface (as illustrated in Figure 8). In this orientation H-bonding occurs and increases the stability of the water layer surrounding the bubble (the hydration layer). For bubbles to coalesce this hydrated layer must be disrupted which requires energy.
The so-called gas dispersion parameters have been studied intensively over the last 20 years [43] - [45] . These parameters comprise superficial gas velocity (Jg), gas holdup (Eg), bubble size (Db) and bubble surface area flux (Sb). Several research groups [5] [43] [46] - [49] have shown that the overall flotation rate constant increases as bubble size is reduced. More commonly today this effect is incorporated in the bubble surface area flux, Sb, which combines the effect of superficial gas velocity (Jg) and Sauter mean bubble size (D32) (Sb = 6 Jg/D32). Figure 2 shows results plotted as rate constant vs. bubble surface area flux giving a close to linear relationship. This figure shows that the effect of frother in controlling bubble size is highly relevant to flotation.
Figure 2. Flotation rate constant versus bubble surface area flux in four industrial flotation machines (adapted from [41] ).
Gas holdup (Eg) in the 2-phase system is readily determined from the hydrostatic pressure difference measured over a set distance in the pulp. In the 3-phase systems Eg measurements can be accomplished using conductivity [45] [50] . Frother concentration influences Eg by controlling bubble size and bubble rise velocity. Azgomi et al. [51] showed that frother type had an effect on gas holdup in addition to its role in controlling bubble size. This was later traced to an effect of frother type on bubble rise velocity [52] [53] . The mechanisms at play the surface of a bubble rising through a frother solution are shown in the Figure 3.
As Figure 3 shows, based on the Frumkin-Levich theory [54] , frother molecules adsorb on the leading surface of bubbles, which are then transported to the rear of the bubble in response to drag from the liquid as the bubble rises. The bubble is said to be mobile. This results in a lowering of surface tension at the bubble rear compared to the front creating a difference in the surface tension with a positive gradient (i.e., a force) directed towards the upper region. This force is in a direction opposite to the flow of liquid and consequently reduces the mobility of the surface. This decrease in mobility makes the bubbles behave more like hollow solid spheres; the surface is said to be more “rigid”.
The decrease in the velocity of an air bubble due to frother is pronounced, as shown in Figure 4 (the frother selected is MIBC and the single bubble diameter was ca. 1.5 mm with measurements at 3 m in a column). The effect of the surface tension gradient force is apparent also in the bubble resisting deformation. There is a relationship between shape and velocity [55] [56] .
As shown in Figure 5, velocity increases with bubble size over the range of interest in flotation (ca. 0.5 to 2.5 mm) [57] . The figure reveals the effect of the frother concentration as the “contaminated water” plot. The combination of bubble size, velocity and frother type/concentration has a profound impact on the gas holdup in the pulp. The same combination also affects shape oscillation [56] with as yet unexplored implications to flotation.
Cappuccitti and Nesset [58] , based on the work of Azgomi et al. [51] and Moyo et al. [26] , explored a possible method to classify frothers using gas holdup (Eg) vs. froth height to try to capture the two frother functions (control of bubble size and froth stability). The relationships readily identify frothers giving more control over froth stability (polyglycols) from those giving more control over gas holdup/bubble size (alcohols).
Finch et al. [47] investigated the relationship between Eg and Sb using data from several sources, proposing that Sb can be determined from gas holdup (Sb ~ 5.5Eg). This implies a consistent relationship between gas holdup and bubble size. The results from Azgomi et al. [51] examined the correspondence of gas holdup with bubble size, an example being Figure 6(a). This shows the relationship is not straightforward: at low concentration while bubble size is decreasing gas holdup remains almost constant while at high concentration bubble size (at least the D32) becomes constant and gas holdup continues to increase. Figure 6(b) offers a possible explanation: at low concentration (e.g. <5 ppm) bubble rise velocity is not decreasing while at high concentration it is continuing to decrease.
Azgomi et al. [51] found a frother type effect: for instance, n-pentanol and F150 could give the same gas holdup but with bubbles in n-pentanol being significantly smaller than F150. This implies bubbles in n-pentanol rise faster than equal-sized bubbles in F150 and this proved to be the case, for bubbles in swarms [53] and for single bubbles [52] . To interpret the effect of solids, the competing influences on bubble size and velocity must be considered.
Figure 3. A cross-section view of an air bubble rising through a frother solution (after [41] ).


Figure 4. Single bubble (dia. 1.5 mm) velocity at 3 m from point of origin (a) versus MIBC concentration; (b) versus rising time (10 ppm MIBC as a example) (data provided by [59] ).
Figure 5. Experimental data for rising velocity of single bubbles (adopted from [57] ).


Figure 6. (a) Gas holdup and bubble size vs. frother concentration [51] ; (b) Gas holdup and single bubble rising velocity vs. frother concentration [51] [59] .
3.2. In the Froth
The froth zone (illustrated in Figure 7) contributes to the flotation process by providing transport to the overflow of the collected (hydrophobic) minerals and rejecting entrained gangue by drainage back to the pulp. Various parameters have been used to describe froth zone behavior among them: target mineral recovery, entrained solids recovery and water recovery [5] . The presence of frother is considered to provide froth stability by retarding bubble coalescence. The mechanisms are those already introduced based on surface tension and surface hydration with an additional one sometimes considered based on bubble surface charge [33] [60] . Mineralized air bubbles also contribute to froth stabilization [20] . The mechanism is mechanical, the particles providing a barrier to coalescence although for nano-sized particles there is evidence of surface tension depression suggestive of a chemical (frother-like) effect [61] .
Analysis of froths has considered thermodynamic aspects [63] and kinetics [64] . According to Shkodin and Tikhomivova [64] at the first stage of froth formation (i.e., at the base of the froth), bubbles are separated by a liquid film in the order of ca. 1 µm. The film is bounded by solvated envelopes (hydrated layers) with properties different from those of the “free” water, as illustrated in Figure 8. On drainage the film thins and the hydrated layers come into contact between neighbouring bubbles. The next stage involves removal of the liquid in the two contacting hydration layers. Depending on the nature of the hydration layer, which reflects the surfactant type, drainage and coalescence can be rapid (e.g. with alcohol frothers) or the film be more persistent (e.g. with some polyglycols, and by common experience soaps and detergents). Gravity and capillary effects in addition to the properties of the hydration layer govern the water drainage. The resultant transition in bubble size as froth ages

Figure 7. (a) The general observation of 2-dimentional froth; (b) Froth structure changes (i.e. coarsening) as it drains (adopted from [62] ).
Figure 8. Frother alignment at the bubble surface and the formation of the “bound” and “free” layers (after [40] ).
(i.e., transition in the vertical direction) is illustrated in Figure 7. This remains the general understanding, at least in the absence of solid particles.
Mechanistic modeling of froths related to flotation systems has accelerated over the last decade. The starting description (e.g. [65] ) sees bubbles in the froth as surrounded by thin lamellae (the hydrated layer) and when three (or more) bubbles meet, a “reservoir” (Plateau border region) is formed at the intersection (Figure 9). Most of the water in froth is contained in the Plateau border region with only a small fraction residing in the lamellae.
Cilliers and co-workers [65] - [67] developed fundamental (i.e., physics-based) models to predict water overflow (JwO) from foam (2-phase froth). Central to the development was the concept of air recovery, α, the fraction of air entering the foam that leaves as unbroken bubbles. Their analysis resulted in two relationships [65] depending on the air recovery. In terms of the symbols used in this proposal, these relationships are:
 (1)
(1)
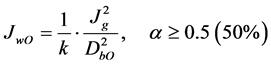 (2)
(2)
where constant k represents the balance between gravity and viscosity, expressed as:
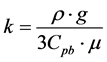 (3)
(3)
where ρ, µ, g is liquid density (g/cm3), kinetic viscosity (g/cm×s) and the gravitational constant (cm/s2), respec-
Figure 9. Schematic of the Plateau border at the junction of three bubbles in the froth.
tively, and Cpb is the viscous drag coefficient in the Plateau border. To balance the units, the unit of constant k is cm−1∙s−1.
In Equation (1), α < 0.5 represents unstable, shallow froth, which creates an overflow rate that depends closely on α (since more than 50% of the air in froth bubbles is lost to bursting before overflowing). When the froth becomes stable, α > 0.5 (Equation (2)), α bubble bursting can be neglected and the water overflow rate becomes independent of α. Note that the bubble size to calculate JwO is the mean bubble size flowing over the lip.
Regardless of α, both relationships show JwO varies with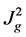 , which is supported by some work [6] [65] . The experimental data of Neethling et al. is shown in Figure 10 on log-log axes. The linear data trend showed the power law and the calculated exponent of 1.97 is close to the predicted value of 2 in Equations (1) & (2). The experimental results of Engelbrecht and Woodburn, [68] and Quinn [69] , however, show that the water overflow rate JwO increases linearly with the air rate Jg. A recent modification to the theory opens a possible reconciliation with these data [66] . An experimental difficulty is that varying Jg also varies DbI and likely influences DbO. Further investigations are required.
, which is supported by some work [6] [65] . The experimental data of Neethling et al. is shown in Figure 10 on log-log axes. The linear data trend showed the power law and the calculated exponent of 1.97 is close to the predicted value of 2 in Equations (1) & (2). The experimental results of Engelbrecht and Woodburn, [68] and Quinn [69] , however, show that the water overflow rate JwO increases linearly with the air rate Jg. A recent modification to the theory opens a possible reconciliation with these data [66] . An experimental difficulty is that varying Jg also varies DbI and likely influences DbO. Further investigations are required.
Moyo et al. [26] found that water overflow rate correlated against gas holdup in the pulp zone and the trends were unique to frother type. Zhang et al. [70] - [81] introduced a way to estimate bubble surface area flux to overflow (SbO) given by:

and showed the water overflow rate was vs. SbO was also unique to frother type. The use of bubble surface area flux will be a feature of the proposed work.
4. Bubble-Particle Attachments
The flotation rate constant (k) is a function of the probability (P) of collection, which is the product of the probability of collision, attachment and non-detachment [82] [83] . From first principles arguments, Jameson et al. [83] derived:

The same authors summarized the available experimental evidence, reporting:






Penafiel and Dobby [84] conducted experiments using hydrophobized (with amine) silica particles to test the effect of bubble size between 1.0 cm/s and 2.5 cm/s Jg in a flotation column. They found:



Figure 10. Experimental relationship between gas rate and water overflow rate on log-log axis (captured from [65] ).
Following the definition of P, one can write [82] [85] [86] :

where Pc is the probability of collision between particles and bubbles; Pa is the probability of adhesion between particles and bubbles; and Pd is the probability of detachment.
Heindel and Bloom [87] modeled the probability of collision under idealized conditions of a spherical bubble rising in a suspension of fine, spherical particles of uniform size (Figure 11), deriving:

where dc is the diameter within which particles collide with the rising bubble (particles outside dc are swept around the bubble by the water streamlines).
As Figure 11 shows, fine particles follow the fluid streamlines (which are always assumed as to come closest to the bubble at its equator). A particle-grazing trajectory therefore can be defined as the one at the bubble equator passing within the distance of the particle radius from the bubble surface [87] [88] . It then can be inferred that only the particles located within the critical diameter dc (defined at infinite distance from the bubble) can collide with the bubble. The dc depends on the bubble and particle Reynolds number.
The most common modeling approach to collision is based on the particle-grazing trajectory. Reay and Ratcliff [90] and Yoon and Luttrell [85] developed derived similar models for the probability of collision, Pc, where B and n are parameters that depend on the bubble Reynolds number (Table 1).

Equation (11) was shown to apply to collection of fine hydrophobic coal in the intermediate range of bubble Reynolds number. Equation (11) implies for fine particles and small bubbles (db < 100 µm), Pc varies as db-2 and hence the flotation rate constant k varies as db-3 (from Equation (5)). This stimulated interest in generating fine bubbles to take advantage of this apparent strong dependence on bubble size. The theoretical observations are in reasonable agreement with the empirical expression Equation (6).
The empirical evidence indicated in Equations (6) and (8), and the model given in Eqn. 11 reveal a strong dependence of the flotation rate constant on the particle size and bubble size. This dependence was summarized by Rubinstein and Samygin [91] (Figure 12). The plot shows a single valued monotonically decreasing dependence on bubble size for k, at constant particle size. However, the k shows a single maximum when plotted against size at constant bubble size. This implies either too fine or too coarse solid particles would reduce k.
There is an objection to this strong dependence on bubble size. Compare to Figure 12, Figure 2 shows a li-
Figure 11. Particle colliding with a bubble at its equator (after [89] ).
Figure 12. Dependence of rate constant of coal flotation upon particle diameter dp and bubble diameter db (adopted from [91] ).
Table 1. The corresponding values of B and n on varying Reynolds number after [85] ).
near k-Sb relationship implying a k-(db)−1 dependence. The difference between the two may be that actual flotation, as in Figure 2, works with bubble and particle size distributions that hide the relationships apparent when idealized systems are tested. Hernandez-Aguilar et al. [92] measured k-Sb on micro-scale with bubble size distributions and found that a linear k-Sb (i.e., k-(db)−1) was adequate but cautioned that the data, even though collected using closely controlled conditions, could be fitted to other db functions as well.
5. The Role of Particles in the 3-Phase Froth
The basic principles derived from the study of 2-phase froth (foam) are applicable to the 3-phase case with the presence of solids being the added factor. The presence of solids in the froth may enhance stability or, may have an adverse effect. According to Frye and Berg [93] and Tao et al. [94] , small (0.2 - 0.5 µm) non-wetting (hydrophobic) particles which have high contact angles (θ > 90˚) promote coalescence (rupture of the thin film between bubbles) and consequently promote froth instability. Dippenaar [30] elegantly showed this phenomenon where, because of the non-wetting nature of the particle, the liquid film spontaneously withdraws from an intruding particle. Particle size and shape were additional factors in the rate of withdrawal.
To investigate the effect of solid particles on bubble coalescence, Spyridopoulos et al. [95] generated two bubbles of equal size (db = 900 µm) in pure distilled water and forced them into contact with a small particle in between. The result was recorded by high-speed photography. Some of the findings are shown in Figure 13.
Figure 13(a) shows the case of a hydrophilic particle (particle size dp = 60 µm and contact angle θ = 32˚) initially loosely suspended by the upper bubble (because of the finite contact angle). As the bottom bubble is moved upwards, the particle is pushed away to the side and has no effect on the approach. For the hydrophobic particle case, Figure 13(b) shows the situation is different. Almost immediately after the bottom bubble comes in contact with the particle, the particle is drawn into the second bubble. The penetration results in rupture of the liquid film and consequent bubble coalescence. The interaction is fast, less than 6 ms for the conditions depicted.
By using a special “froth viewing chamber”, Ata et al. [96] demonstrated that entrained hydrophilic particles (silica) decreased bubble coalescence rate. They claimed the main reason was an increase in the slurry viscosity of the liquid between the bubbles and mechanical blockage of drainage channels. Bulatovic [97] also suspects froth stabilization with hydrophilic particles. To estimate the inter-bubble slurry viscosity, one possibility is the expression from Chung and Adelman [98] :



Figure 13. (a) A hydrophilic particle between two approaching bubbles (adopted from [95] ); (b) A hydrophobic particle forms immediately a second 3-phase contact line (adopted from [95] ).

where µ is viscosity of water; µ* is viscosity of slurry; φsis volumetric fraction of solids in slurry, and can be calculated by using Equation (13); ρ is density of liquid; ρsis density of solid; Xsis solid concentration in slurry.
The time to rupture the film is related to the hydrophobicity, size and shape of the particles since these factors determine the degree of penetration of the particles into the film. Bulatovic [97] proposed an equation to show how the governing factors relate to the rate of film thinning:

where δ is the film thickness at distance z, η is the viscosity of slurry, ρ is the density of the particles, t is the time when the film became parabolic.
Many studies on the role of particles in coalescence do not always include frother. Bulatovic [97] studied froth stability with hydrophobic quartz particles (θ = 102˚) of varying size (400 - 5 µm). He concluded that these very hydrophobic particles at all sizes can destroy froth unless frother was present. This argues that in the presence of very hydrophobic particles, the stabilizing effect in the froth is almost completely provided by the frother used.
The above experimental scenarios do not specifically include the particle loading on the bubble. Particles loaded on bubble provide a barrier, literally preventing the bubbles from contacting and coalescing. This arguably is the situation in actual flotation where collected particles usually enhance froth stability: without this flotation would not occur. Sufficient froth fro flotation can form even without frother provided bubbles are carrying sufficient particles [99] . The reduction in drainage rate is sometimes likened to increasing the liquid viscosity [100] . Finch and Dobby [11] sketched the dependence of froth stability on bubble loading from observations on column froths where low loading could destabilize and high loadings could stabilize. Loading thus needs to be considered in the further study.
6. Adsorption of Frothers on Particles
Adsorption of frother on naturally hydrophobic particles like coal, talc or graphite has been observed and attributed to van der Waals interactions between the hydrophobic part of the frother molecule and the hydrophobic surface of the particles [101] . Investigating the high frother (MIBC) consumption at Century Mine (Australia), Gredeji et al. [102] found that the bulk of MIBC was adsorbed onto ore particles, especially the fine carbon-enriched (i.e., hydrophobic) particles. Likewise, Allum and Whelan [103] reported that two-thirds of frother added was taken up by coal during flotation. Ottewill [104] reviewed the adsorption of various nonionic surfactants on different surfaces. In the case of hydrophobic particles, they concluded that molecules may first adsorb lying “flat”, but at higher concentration the molecules may re-orient into a vertical close-packed monolayer. Kuan and Finch [2009] also observed adsorption of frother by the talc that altered the bubble size and froth characteristics. The use of salts to avoid this adsorption issue, as noted before, may be a solution.
7. Conclusions
1) Measurements of pulp zone properties, bubble size and gas holdup, should help interpret and characterize the pulp properties. The role of frother controlling bubble size and froth properties is reasonably well reviewed;
2) The study of the effect of frothers on bubble terminal velocity is introduced. It shows the interesting revelations of the bubble terminal velocity with different frother type and concentrations. Adding solids as a parameter to the work may provide further insight into the complicated nature of flotation hydrodynamics;
3) Air recovery is demonstrated and has been explained by changes in the structural features of the froth including bubble loading and the flow of bubble surface. It has been suggested that flotation recovery can be improved by operating at the maximum froth stability;
4) Although frothers are added to stabilize froth, froth stability depends more on the amount and properties of the particles attached. The main variable for particles is the type of solids which include hydrophilic gangue and hydrophobic minerals. A secondary variable is particle size. The incorporation of a variety of solids reflects the different mechanisms: hydrophilic particles are expected to concentrate in the interstitial water between bubbles (within the froth) while hydrophobic particles will accumulate at the bubble liquid-air interface;
5) The study of effect of particles on bubble thin films is explored. The entrained hydrophilic particles decreased bubble coalescence rate was demonstrated. The reason was revealed as an increase in the slurry viscosity of the liquid between the bubbles and mechanical blockage of drainage channels;
6) The decrease in frother concentration due to the adsorptions/interactions between frothers and particles was detected. It was suggested that talc could remove F150 directly from the bubble surface and increase coalescence rate, however the literature did not offer a complete explanation.
Cite this paper
Wei Zhang,1 1, (2016) The Effects of Frothers and Particles on the Characteristics of Pulp and Froth Properties in Flotation—A Critical Review. Journal of Minerals and Materials Characterization and Engineering,04,251-269. doi: 10.4236/jmmce.2016.44023
References
- 1. Leja, J. and Schulman, J.H. (1954) Flotation Theory: Molecular Interactions between Frothers and Collectors at Solid-Liquid-Air Interfaces. Transactions of the Metallurgical Society of AIME, 199, 221-228.
- 2. Crozier, R. and Klimpel, R. (1989) Frothers: Plant Practice. In: Laskowski, J., Ed., Frothing in Flotation, Chapter 11, Gordon and Breach Science Publishers, New York, 257-280.
- 3. Klimpel, R. and Isherwood, S. (1991) Some Industrial Implications of Changing Frother Chemical Structure. International Journal of Mineral Processing, 33, 369-381. http://dx.doi.org/10.1016/0301-7516(91)90064-P
- 4. Wheeler, T. (1994) Coal Floats by Itself—Doesn’t It? In: Sibrell, P.L. and Watten, B.J., Eds., Reagents for Better Metallurgy, Colorado Society for Mining and Metallurgy, and Exploration Inc., Denver, 131-142.
- 5. Comley, B.A., Vera, M.A. and Franzidis, J.P. (2007) Interpretation of the Effect of Frother Type and Concentration on Flotation Performance in an OK3 Cell. Mineral and Metallurgical Processing, 24, 243-252.
- 6. Stevenson, P. (2006) The Wetness of a Rising Foam. Industrial & Engineering Chemistry Research, 45, 803-807. http://dx.doi.org/10.1021/ie050860u
- 7. Grau, R.A., Laskowski, J.S. and Heiskanen, K. (2005) Effect of Frothers on Bubble Size. International Journal of Mineral Processing, 76, 225-233. http://dx.doi.org/10.1016/j.minpro.2005.01.004
- 8. Finch, J.A., Nesset, J.E. and Acuna, C. (2008) Role of Frother on Bubble Production and Behaviour in Flotation. Minerals Engineering, 21, 949-957. http://dx.doi.org/10.1016/j.mineng.2008.04.006
- 9. Quinn, J.J., Kracht, W., Gomez, C.O., Gagnon, C. and Finch, J.A. (2007) Comparing the Effect of Salts and Frother (MIBC) on Gas Dispersion and Froth Properties. Minerals Engineering, 20, 1296-1302. http://dx.doi.org/10.1016/j.mineng.2007.07.007
- 10. Kuan, H. and Finch, J.A. (2010) Impact of Talc on Pulp and Froth Properties in F150 and 1-Pentanol Frother Systems. Minerals Engineering, 23, 1003-1009. http://dx.doi.org/10.1016/j.mineng.2010.04.010
- 11. Finch, J.A. and Dobby, G.S. (1990) Column Flotation. Pergamon Press, New York.
- 12. Dahlke, R.C., Gomez, C.O. and Finch, J.A. (2005) Operating Range of a Flotation Cell Determined from Gas Holdup vs. Gas Rate. Minerals Engineering, 18, 977-980. http://dx.doi.org/10.1016/j.mineng.2004.12.013
- 13. Finch, J.A., Cilliers, J. and Yianatos, J. (2007) Column Flotation, Section I: The Collection Zone. In: Fuerstenau, M.C., Jameson, G. and Yoon, R.-H., Eds., Froth Flotation-A Century of Innovation, Society for Mining Metallurgy & Exploration, Sydney, 121-127.
- 14. Mena, P.C., Ruzicka, M.C., Teixeira, J.A. and Drahos, J. (2005) Effect of Solids on Homogeneous-Heterogeneous Flow Regime in Bubble Columns. Chemical Engineering Science, 60, 6013-6026. http://dx.doi.org/10.1016/j.ces.2005.04.020
- 15. Banisi, S., Finch, J.A., Laplante, A.R. and Weber, M.E. (1995) Effect of Solid Particles on Gas Holdup in Flotation Columns-I. Measurement. Chemical Engineering Science, 50, 2335-2342. http://dx.doi.org/10.1016/0009-2509(95)00076-H
- 16. Garibay, R.P., Gallegos, P.M., Uribe-Salas, A. and Nava, F. (2002) Effect of Collection Zone Height and Operating Variables on Recovery of Overload Flotation Columns. Minerals Engineering, 15, 325-331. http://dx.doi.org/10.1016/S0892-6875(02)00035-3
- 17. Gomez, C., Uribe-Salas, A., Huls, B. and Finch, J.A. (1995) Axial Gas Holdup Profiles in the Collection Zone of Flotation Columns. Mineral and Metal Processing, 12, 16-23.
- 18. Stevenson, P., Stevanov, C. and Jameson, G. J. (2003) Liquid Overflow From a Column of Rising Aqueous Froth. Minerals Engineering, 16, 1045-1053. http://dx.doi.org/10.1016/j.mineng.2003.05.004
- 19. Neethling, S.J. and Cilliers, J.J. (2009) The Entrainment Factor in Froth Flotation: Model for Particle Size and Other Operating Parameters Effects. International Journal of Mineral Processing, 93, 141-148. http://dx.doi.org/10.1016/j.minpro.2009.07.004
- 20. Hunter, T.N., Pugh, R.J., Franks, G.V. and Jameson, G.J. (2008) The Role of Particle in Stabilising Foams and Emulsions. Advances in Colloid and Interface Science, 137, 57-81. http://dx.doi.org/10.1016/j.cis.2007.07.007
- 21. Alexander, D., Franzidis, J.P. and Manlapig, E. (2003) Froth Recovery Measurement in Plant Scale Flotation Cells. Minerals Engineering, 16, 1197-1203. http://dx.doi.org/10.1016/j.mineng.2003.07.016
- 22. Seaman, D., Franzidis, J.P. and Manlapig, E. (2004) Bubble Load Measurement in the Pulp Zone of Industrial Flotation Machines: A New Device for Determining the Froth Recovery of Attached Particles. International Journal of Minerals Processing, 74, 1-13. http://dx.doi.org/10.1016/j.minpro.2004.04.001
- 23. Barbian, N., Hadler, K. and Cilliers, J.J. (2006) The Froth Stability Column: Measuring Froth Stability at an Industrial Scale. Minerals Engineering, 19, 713-718. http://dx.doi.org/10.1016/j.mineng.2005.09.021
- 24. Zanin, M., Ametov, I., Grano, S., Zhou, L. and Skinner, W. (2009) A Study of Mechanisms Affecting Molybdenite Recovery in a Bulk Copper/Molybdenum Flotation Circuit. International Journal of Mineral Processing, 93, 256-266. http://dx.doi.org/10.1016/j.minpro.2009.10.001
- 25. Zanin, M., Wightman, E., Grano, S.R. and Franzidis, J.P. (2009) Quantifying Contributions to Froth Stability in Porphyry Copper Plants. International Journal of Mineral Processing, 91, 19-27. http://dx.doi.org/10.1016/j.minpro.2008.11.003
- 26. Moyo, P., Gomez, C.O. and Finch, J.A. (2007) Characterizing Frothers Using Water Carrying Rate. Canadian Metallurgical Quarterly, 46, 215-220. http://dx.doi.org/10.1179/cmq.2007.46.3.215
- 27. Sweet, C., van Hoogstraten, J., Harris, M. and Laskowski, J.S. (1997) The Effect of Frothers on Bubble Size and Frothability of Aqueous Solutions. Processing of Complex Ores, Metallurgical Society of CIM, Montreal, 10-12 October 1997, 235-245.
- 28. Cappuccitti, F., Finch, J.A., Nesset J.E. and Zhang W. (2009) Characterization of Frothers and Its Role in Flotation Optimization. Proceedings of the 2009 SME Annual Meeting & Exhibit and Colorado Mining Association, 111th National Western Mining Conference, Denver, 12 June 2009, 481-484.
- 29. Melo, F. and Laskowski, J.S. (2006) Fundamental Properties of Flotation Frothers and Their Effect on Flotation. Minerals Engineering, 19, 766-773. http://dx.doi.org/10.1016/j.mineng.2005.09.031
- 30. Dippenaar, A. (1982) The Destabilization of Froth by Solids. I. the Mechanisms of Film Rupture. International Journal of Mineral Processing, 9, 1-14. http://dx.doi.org/10.1016/0301-7516(82)90002-3
- 31. Johansson, G. and Pugh, R.J. (1992) The Influence of Particle Size and Hydrophobicity on the Stability of Mineralized Froths. International Journal Mineral Processing, 34, 1-21. http://dx.doi.org/10.1016/0301-7516(92)90012-L
- 32. Schwarz, S. and Grano, S. (2005) Effect of Particle Hydrophobicity on Particles and Water Transport across a Flotation Froth. Colloids and Surfaces A, 256, 157-164. http://dx.doi.org/10.1016/j.colsurfa.2005.01.010
- 33. Pugh, R.J., Weissenborn, P. and Paulson, O. (1997) Flotation in Inorganic Electrolytes, the Relationship between Recovery of Hydrophobic Particles, Surface Tension, Bubble Coalescence and Gas Solubility. International Journal of Mineral Processing, 51, 125-138. http://dx.doi.org/10.1016/S0301-7516(97)00021-5
- 34. Laskowski, J.S. (1998) Frothers and Flotation. In: Laskowski, J.S. and Woodburn, E.T., Eds., Frothing in Flotation II, Ch. 1, CRC Press, Boca Raton, 1-49.
- 35. Cytec Mining Chemicals Handbook (2002) 75-78.
- 36. Azgomi, F., Gomez, C.O. and Finch, J.A. (2009) Frother Persistence: A Measure Using Gas Holdup. Minerals Engineering, 22, 874-878. http://dx.doi.org/10.1016/j.mineng.2009.03.013
- 37. Harris, C.C. (1976) Flotation Machines in Flotation. In: Gaudin, A.M., Ed., Memorial Volume, Vol. 2, Ch. 27, American Institute of Mining, Metallurgical, and Petroleum Engineers, Inc., New York, 753-815.
- 38. Metso Minerals CBT (Computer Based Training) (2002) Mill Operator Training Package: Flotation Module. Formerly Brenda Process Technology CBT (Computer Based Training).
- 39. Cho, Y.S. and Laskowski, J.S. (2002) Effect of Flotation Frothers on Bubble Size and Foam Stability. International Journal of Mineral Processing, 64, 69-80. http://dx.doi.org/10.1016/S0301-7516(01)00064-3
- 40. Gélinas, S. and Finch, J.A. (2005) Colorimetric Determination of Common Industrial Frothers. Minerals Engineering, 18, 263-266. http://dx.doi.org/10.1016/j.mineng.2004.08.020
- 41. Nguyen, A.V. and Schulze, H.J. (2004) Colloidal Science of Flotation. In: Nguyen, A.V. and Schulze, H.J., Eds., Surfactant Science Series, Marcel Dekker Inc., New York, 27-34.
- 42. Wang, L. and Yong, R.H. (2008) Effects of Surface Forces and Film Elasticity on Foam Stability. International Journal of Mineral Processing, 85, 101-110. http://dx.doi.org/10.1016/j.minpro.2007.08.009
- 43. Gorain, B.K., Franzidis, J.P. and Manlapig, E.V. (1997) Studies on Impeller Type, Impeller Speed and Air Flow Rate in an Industrial Scale Flotation Cell: Part 4: Effect of Bubble Surface Area Flux on Flotation Performance. Minerals Engineering, 10, 367-379. http://dx.doi.org/10.1016/S0892-6875(97)00014-9
- 44. Hernandez, H., Gomez, C.O. and Finch, J.A. (2003) Gas Dispersion and De-Inking in a Flotation Column. Mineral Engineering, 16, 739-744. http://dx.doi.org/10.1016/S0892-6875(03)00170-5
- 45. Gomez, C.O. and Finch, J.A. (2007) Gas Dispersion Measurements in Flotation Cells. International Journal of Mineral Processing, 84, 51-58. http://dx.doi.org/10.1016/j.minpro.2007.03.009
- 46. Luttrell, G. and Yoon, R. (1992) A Hydrodynamic Model for Bubble Particle Attachment. Journal of Colloid and Interface Science, 154, 129-137. http://dx.doi.org/10.1016/0021-9797(92)90085-Z
- 47. Finch, J.A., Gomez, C.O., Hardie, C., Leichtl, E.G., Filippone, R. and Leroux, D. (1999) Bubble Surface Area Flux: A Parameter to Characterise Flotation Cells. Proceedings of the 31st Canadian Mineral Processors Conference, Ottawa, 12-17 January 1999, 199-210.
- 48. Deglon, D.A., Egya-Mensah, D. and Franzidis, J.P. (2000) Review of Hydrodynamics and Gas Dispersion in Flotation Cells on South African Platinum Concentrators. Minerals Engineering, 13, 235-244. http://dx.doi.org/10.1016/S0892-6875(00)00003-0
- 49. Hernandez, H., Gomez, C.O. and Finch, J.A. (2001) A Test of Flotation Rate Constant vs. Bubble Surface Area Flux Relationship in Flotation. In: Finch, J.A., Rao, S.R. and Huang, L., Eds., Interactions in Mineral Processing, Interactions in Mineral Processing: Proceedings of the 4rth UBC-McGill International Symposium on Fundamentals of Mineral Processing. 4th UBC-McGill International Symposium Fundamentals of Mineral Processing, Toronto, 26-29 August 2001, 181-200.
- 50. Gomez, C.O., Cortés-López, F. and Finch, J.A. (2003) Industrial Testing of a Gas Holdup Sensor for Flotation Systems. Mineral Engineering, 16, 493-501. http://dx.doi.org/10.1016/S0892-6875(03)00083-9
- 51. Azgomi, F, Gomez, C.O. and Finch, J.A. (2007) Correspondence of Gas Holdup and Bubble Size in Presence of Different Frothers. International Journal of Mineral Processing, 83, 1-11. http://dx.doi.org/10.1016/j.minpro.2007.03.002
- 52. Rafiei, A.A., Finch, J.A. (2009) A Comparison of Bubble rise Velocity Profile of Two Surfactants to Explain Gas Holdup Data. Proceedings 48th Conference of Metallurgists, Sudbury, 23-26 August 2009, 183-192.
- 53. Acuna, C.A. and Finch, J.A. (2010, Tracking Velocity of Multiple Bubbles in a Swarm. International Journal of Mineral Processing, 94, 147-158. http://dx.doi.org/10.1016/j.minpro.2010.02.001
- 54. Frumkin, A.N. and Levich, V.G. (1947) The Effect of Surface Active Agents on Motion at the Boundary of the Liquid Medium. Journal of Physical Chemistry, 4, 41-45.
- 55. Wu, M. and Gharib, M. (2002) Experimental Studies on the Shape and Path of Small Air Bubbles Rising in Clean Water. Physics of Fluids, 14, 49-52. http://dx.doi.org/10.1063/1.1485767
- 56. Kracht, W. and Finch, J.A. (2009) Bubble Break-Up and the Role of Frother and Salt. International Journal of Mineral Processing, 92, 153-161. http://dx.doi.org/10.1016/j.minpro.2009.03.011
- 57. Clift, R., Grace, J.R. and Weber, M.E. (1978) Bubbles, Drops and Particles. Academic Press, New York.
- 58. Cappuccitti, F. and Nesset, J.E. (2009) Frother and Collector Effects on Flotation Cell Hydrodynamics and Their Implication on Circuit Performance. Proceedings 48th Conference of Metallurgists, Sudbury, 23-26 August 2009, 169-182.
- 59. Tan, Y.H. (2010) Private Communications. McGill University, Montreal.
- 60. Kitchener, J.A. and Cooper, C.F. (1959) Current Concepts in the Theory of Foaming. Quarterly Reviews, Chemical Society, 13, 71-97. http://dx.doi.org/10.1039/qr9591300071
- 61. Blute, I., Pugh, R.J., van de Pas, J. and Callaghan, I. (2009) Industrial Manufactured Silica Nanoparticle Sols. 2: Surface Tension, Particle Concentration, Foam Generation and Stability. Colloids and Surfaces A, 337, 127-135. http://dx.doi.org/10.1016/j.colsurfa.2008.12.009
- 62. Weaire, D. and Hutzler, S. (1999) The Physics of Foam. Clarendon Press, Oxford.
- 63. Rehbinder, P.A. (1950) The Problems of Emulsions and Froths in the Food Industry. Colloids in the Food Industry, Pishchepromizdaz, Moscow.
- 64. Shkodin, A.M. and Tikhomivova, G.P. (1951) Frothing in Mixtures of Surface-Active Colloids. Colloid Journal, 2, 19-26.
- 65. Neethling, S.J., Lee, H.T. and Cilliers, J.J. (2003) Simple Relationships for Predicting the Recovery of Liquid from Flowing Foams and Froths. Minerals Engineering, 16, 1123-1130. http://dx.doi.org/10.1016/j.mineng.2003.06.014
- 66. Neethling, S.J. and Cilliers, J.J. (2010) Private Communications.
- 67. Neethling, S.J. and Cilliers, J.J. (2002) The Entrainment of Gangue into a Flotation Froth. International Journal of Mineral Processing, 64, 123-134. http://dx.doi.org/10.1016/S0301-7516(01)00067-9
- 68. Engelbrecht, J. A. and Woodburn, E. T. (1975) The Effects of Froth Height, Aeration Rate and Gas Precipitation on Flotation. Journal of the South African Institute of Mining & Metallurgy, 76, 125-32.
- 69. Quinn, J. (2006) Exploring the Effects of Salts on Gas Dispersion and Froth Properties in Flotation Systems. Master’s Thesis, Department of Mining and Materials Engineering, McGill University, Montreal.
- 70. Zhang W., Kolahdoozan M., Nesset J.E. and Finch J.A. (2009) Use of Frother with Sampling-for-Imaging Bubble Sizing Technique. Minerals Engineering, 22, 513-515. http://dx.doi.org/10.1016/j.mineng.2008.11.004
- 71. Zhang, W., Nesset, J.E. and Finch, J.A. (2010) Water Recovery and Bubble Surface Area Flux in Flotation. Canadian Metallurgical Quarterly, 49, 353-362. http://dx.doi.org/10.1179/cmq.2010.49.4.353
- 72. Zhang, W., Nesset, J.E., Rao, S.R. and Finch, J.A. (2012) Characterizing Frothers through Critical Coalescence Concentration (CCC)95-Hydrophile-Lipophile Balance (HLB) Relationship. Minerals, 2, 208-227. http://dx.doi.org/10.3390/min2030208
- 73. Zhang, W., Zhou, X. and Finch, J.A. (2012) Determining Independent Control of Dual-Frother Systems-Gas Holdup, Bubble Size and Water Overflow Rate. Minerals Engineering, 39, 106-116. http://dx.doi.org/10.1016/j.mineng.2012.08.008
- 74. Zhang W., Zhu S. and Finch, J.A. (2013) Frother Partitioning in Dual-Frother Systems: Development of Analytical Technique. International Journal of Mineral Processing, 119, 75-82. http://dx.doi.org/10.1016/j.minpro.2013.01.002
- 75. Finch J.A. and Zhang W. (2014) Frother Function-Structure Relationship: Dependence of CCC95 on HLB and the H-Ratio. Minerals Engineering, 61, 1-8. http://dx.doi.org/10.1016/j.mineng.2014.02.006
- 76. Zhang W. (2014) Evaluation of Effect of Viscosity Changes on Bubble Size in a Mechanical Flotation Cell. Transactions of Nonferrous Metals Society of China, 24, 2964-2968. http://dx.doi.org/10.1016/S1003-6326(14)63432-4
- 77. Zhang W. and Finch J.A. (2014) Effect of Solids on Pulp and Froth Properties in Flotation. Journal of Central South University, 21, 1461-1469. http://dx.doi.org/10.1007/s11771-014-2086-1
- 78. Zhang W., Nesset J.E. and Finch J.A. (2014) Correspondence of Bubble Size and Frother Partitioning in Flotation. Journal of Central South University, 21, 2383-2390. http://dx.doi.org/10.1007/s11771-014-2191-1
- 79. Zhang W., Nesset J.E. and Finch J.A. (2014) Effect of Some Operational Variables on Bubble Size in a Pilot-Scale Mechanical Flotation Machine. Journal of Central South University, 21, 1077-1084. http://dx.doi.org/10.1007/s11771-014-2039-8
- 80. Zhang W., Nesset J.E. and Finch J.A. (2014) Bubble Size as a Function of Some Situational Variables in Mechanical Flotation Machines. Journal of Central South University, 21, 720-727. http://dx.doi.org/10.1007/s11771-014-1994-4
- 81. Zhang W., Nesset J.E. and Finch J.A. (2014) A Novel Approach to Prevent Bubble Coalescence during Measurement of Bubble Size in Flotation. Journal of Central South University, 21, 338-343. http://dx.doi.org/10.1007/s11771-014-1945-0
- 82. Sutherland, K.L. (1948) Physical Chemistry of Flotation. XI. Kinetics of the Flotation PROCESS. The Journal of Chemical Physics, 52, 394-425. http://dx.doi.org/10.1021/j150458a013
- 83. Jameson, G.J., Nam, S. and Moo-Young, M. (1977) Physical Factors Affecting Recovery Rates in Flotation. Mineral Science Engineering, 9, 103-118.
- 84. Penafiel, D. P. and Dobby, G.S. (1994) Kinetic Studies in Flotation Columns: Bubble Size Effect. Minerals Engineering, 7, 465-478. http://dx.doi.org/10.1016/0892-6875(94)90159-7
- 85. Yoon, R.H., Luttrell, G.H. (1989) The Effect of Bubble Size on Fine Particle Flotation. In: Laskowski, J., Ed., Frothing in Flotation, Gordon and Breach Science, New York, 101-122. http://dx.doi.org/10.1080/08827508908952646
- 86. Yoon, R. (2000) The Role of Hydrodynamic and Surface Forces in Bubble-Particle Interaction. International Journal of Mineral Processing, 58, 129-143. http://dx.doi.org/10.1016/S0301-7516(99)00071-X
- 87. Heindel, T.J. and Bloom, F. (1999) Exact and Approximate Expressions for Bubble-Particle Collision. Journal of Colloid and Interface Science, 213, 101-111. http://dx.doi.org/10.1006/jcis.1999.6112
- 88. Yoon, R. and Mao, L. (1996) Application of Extended DLVO Theory, IV: Derivation of Flotation Rate Equation from First Principles. Journal of Colloid and Interface Science, 181, 613-626. http://dx.doi.org/10.1006/jcis.1996.0419
- 89. Grau, R.A. (2006) An Investigation of the Effect of Physical and Chemical Variables on Bubble Generation and Coalescence in Laboratory Scale Flotation Cells. PhD Thesis, Helsinki University of Technology, Espoo.
- 90. Reay, D., Ratcliff, G. A. (1973) Removal of Fine Particles from Water by Dispersed Air Flotation: Effects of Bubble Size and Particle Size on Collection Efficiency. The Canadian Journal of Chemical Engineering, 51, 178-185. http://dx.doi.org/10.1002/cjce.5450510207
- 91. Rubinstein, J.B. and Samygin, V.D. (1998) Effect of Particle and Bubble Size on Flotation Kinetics. In: Laskowski, J.S. and Woodburn E.T., Eds., Frothing in Flotation II, Gordon and Breach Science, New York, 51-80.
- 92. Hernandez-Aguilar, J.R., Rao, S.R. and Finch, J.A. (2005) Testing the k-Sb Relationship at the Microscale. Minerals Engineering, 18, 591-598. http://dx.doi.org/10.1016/j.mineng.2004.10.003
- 93. Frye, C.G. and Berg, J.C. (1989) Antifoam Action by Solid Particles. Journal of Colloid and Interface Science, 127, 222-238. http://dx.doi.org/10.1016/0021-9797(89)90023-4
- 94. Tao, D., Luttrell, G.H. and Yoon, R.H. (2000) A Parameter Study of Froth Stability and Its Effect on Column Flotation of Fine Particles. International Journal of Mineral Processing, 59, 25-43. http://dx.doi.org/10.1016/S0301-7516(99)00033-2
- 95. Spyridopoulos, M.T., Simons, S.J.R., Neethling, S.J. and Cilliers, J.J. (2005) Bubble Coalescence Behavior in Dissolved Air Flotation Froths. Centenary of Flotation Symposium, Brisbane, 5-9 June 2005, 923-929.
- 96. Ata, S., Ahmed, N. and Jameson, G.J. (2003) A Study of Bubble Coalescence in Flotation Froths. International Journal of Mineral Processing, 72, 255-266. http://dx.doi.org/10.1016/S0301-7516(03)00103-0
- 97. Bulatovic, S.M. (2007) Handbook of Flotation Reagents. Elsevier, Amsterdam.
- 98. Chung, Y.M. and Adelman, S.A. (1978) Transport Properties of Concentrated Polymer Solutions: Hydrodynamic Mean Field Theory of the Viscosity of a sphere Suspension. The Journal of Chemical Physics, 69, 3146-3149. http://dx.doi.org/10.1063/1.437008
- 99. Pugh, R. (2006) Surface Chemical Studies on Particle-Stabilized Froths. Proceedings of the XXIIIth International Mineral Processing Congress, Istanbul, 3-8 September 2006, 430-435.
- 100. Rao, S.R. and Leja, J. (2004) Surface Chemistry of Froth Flotation. 2nd Edition, Kluwer Academic Publication, New York. http://dx.doi.org/10.1007/978-1-4757-4302-9
- 101. Fuerstenau, D.W. and Pradip (1982) Adsorption of Frothers at Coal/Water Interfaces. Colloids and Surfaces, 4, 229-243. http://dx.doi.org/10.1016/0166-6622(82)80019-X
- 102. Gredelj, S., Zanin, M. and Grano, S.R. (2009) Selective Flotation of Carbon in the Pb-Zn Carbonaceous Sulphide Ores of Century Mine, Zinifex. Minerals Engineering, 22, 279-288. http://dx.doi.org/10.1016/j.mineng.2008.08.005
- 103. Zhang, W., Tan, Y.H. and Finch, J.A. (2016) Synthesis and Characterization of Alkyl, Propoxy, Ethoxy-Based Frothers. Minerals Engineering, 95, 66-73. http://dx.doi.org/10.1016/j.mineng.2016.06.013
- 104. Ottewill, R.H. (1967) Colloidal Properties of Latex Particles. In: Schick, M.C., Ed., Nonionic Surfactants, Ch. 19, Dekker, New York, 129-157.
Nomenclature











