Graphene
Vol.2 No.3(2013), Article ID:34754,5 pages DOI:10.4236/graphene.2013.23014
Next-Nearest-Neighbor Tight-Binding Model of Plasmons in Graphene
1Department of Physics, Bar-Ilan University, Ramat Gan, Israel 2Institut für Physik, Universität Augsburg, Augsburg, Germany
Email: Eugene.Kogan@biu.ac.il
Copyright © 2013 Vladimir Kadirko et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 8, 2013; revised June 7, 2013; accepted July 3, 2013
Keywords: Graphene; Plasmon; Tight-Binding Model
ABSTRACT
In this paper we investigate the influence of the next-nearest-neighbor coupling on the spectrum of plasmon excitations in graphene. The nearest-neighbor tight-binding model was previously considered to calculate the plasmon spectrum in graphene [1]. We extend these results to the next-nearest-neighbor tight-binding model. As in the calculation of the nearest-neighbor model, our approach is based on the numerical calculation of the dielectric function and the loss function. We compare the plasmon spectrum of the two models and discuss the differences in the dispersion.
1. Introduction
Graphene, a single layer of carbon atoms arranged as a honeycomb lattice, is a semimetal with remarkable physical properties [2,3]. This is due to the band structure of the material which consists of two bands touching each other at two nodes. The electronic spectrum around these two nodes is linear and can be approximated by Dirac cones. However, calculations of many physical properties demand the knowledge of the full electron dispersion in the entire Brillouin zone, not only in the vicinity of the nodes. This statement becomes particularly relevant when we take into account the fact that graphene can be gated or doped, such that the Fermi energy can be freely tuned.
One of the main open issues in the physics of graphene is the role played by electron-electron interaction. In doped graphene long range Coulomb interaction leads to a gapless plasmon mode which can be described theoretically within the random phase approximation (RPA). Although this is a standard problem in semiconductor physics, it was studied initially in the case of graphene only in the Dirac approximation around the nodes [4-6]. The linear approximation leads to a frequency of the plasmon that is proportional to the square root of the wavevector.
Later the plasmon dispersion law was also calculated for the more realistic band structure, obtained in the framework of the tight-binding model with nearest-neighbor hopping [1,7]. This model is characterized by two symmetric bands, which implies a chiral symmetry. The latter connects the eigenstates of energy E directly with eigenstates of energy −E by a linear transformation. This symmetry, which also realizes a particle-hole symmetry, is broken by a next-nearest-neighbor hopping term. Usually, the physical properties change qualitatively under symmetry breaking. Here we would like to study the effect of particle-hole symmetry breaking due to next-nearest-neighbor hopping on the plasmon dispersion. For this purpose we extend the nearest-neighbor hopping approximation used in [1] by taking into account the nextnearest-neighbor hopping.
We consider an electron gas which is subject to an electromagnetic potential . The response of the electron gas is to create a screening potential
. The response of the electron gas is to create a screening potential 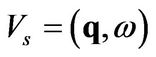 which is caused by the rearrangement of the electrons due to the external potential. Therefore, the total potential, acting on the electrons, is [8]
which is caused by the rearrangement of the electrons due to the external potential. Therefore, the total potential, acting on the electrons, is [8]
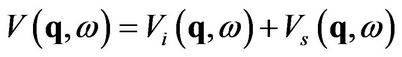 (1)
(1)
can be evaluated self-consistently [9] and is expressed via the dielectric function. Then the total potential reads [8]
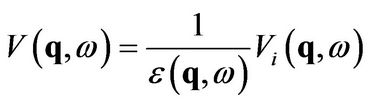 (2)
(2)
2. Nearest and Next-Nearest Hopping Model
The tight-binding Hamiltonian for electrons in graphene with both nearest and next-nearest-neighbor hopping has the form [2] (we use units such that h = 1)
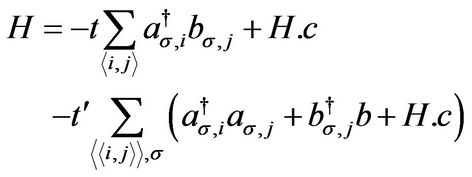 (3)
(3)
where 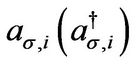 annihilates (creates) an electron with spin
annihilates (creates) an electron with spin 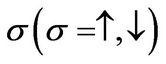 on site Ri on sublattice A (an equivalent definition is used for sublattice B),
on site Ri on sublattice A (an equivalent definition is used for sublattice B), 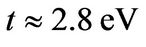 is the nearest-neighbor hopping energy (hopping between different sublattices), and
is the nearest-neighbor hopping energy (hopping between different sublattices), and 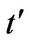 is the next nearest-neighbor hopping integral (hopping in the same sublattice). The value of
is the next nearest-neighbor hopping integral (hopping in the same sublattice). The value of 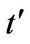 is not well known but ab initio calculations find
is not well known but ab initio calculations find  depending on the tight-binding parametrization [2].
depending on the tight-binding parametrization [2].
The matrix representation of the Hamiltonian is
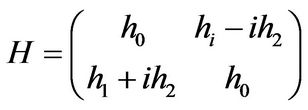 (4)
(4)
The non-diagonal terms in the Hamiltonian correspond to the nearest-neighbor hopping [1]:
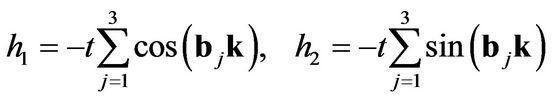 (5)
(5)
where b1,2,3 are the nearest-neighbor vectors on the honeycomb lattice:
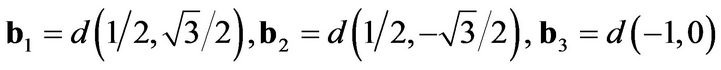
and is the lattice constant (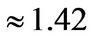 Å) the diagonal terms correspond to next-nearest-neighbor hopping:
Å) the diagonal terms correspond to next-nearest-neighbor hopping:
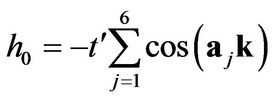 (6)
(6)
where, 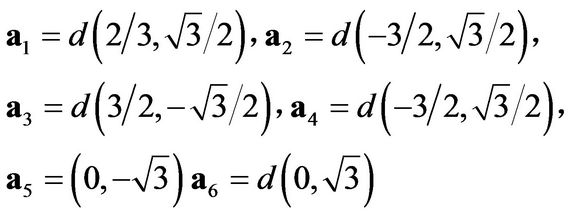
the energy bands derived from this Hamiltonian have the form [2]
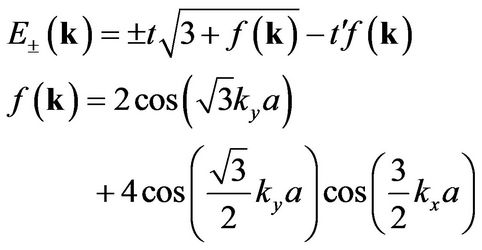 (7)
(7)
where the plus sign applies to the upper (π or conduction) and the minus sign the lower (π* or valence) band. It should be noticed that the presence of  shifts the position of the Dirac point in energy and it breaks electron-hole symmetry. In both cases, nearest-neighbor and next nearest-neighbor hopping, the electronic dispersion is an even function [1]
shifts the position of the Dirac point in energy and it breaks electron-hole symmetry. In both cases, nearest-neighbor and next nearest-neighbor hopping, the electronic dispersion is an even function [1]
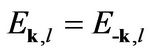 (8)
(8)
The dispersion law for next nearest-neighbor hopping is presented on Figure 1, and the eigenvectors of the Hamiltonian read
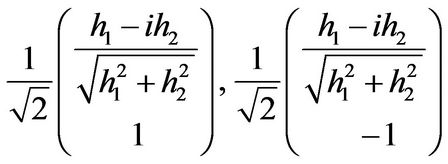 (9)
(9)
where the first eigenvector is for the upper band and the second eigenvector for the lower band.
The Hamiltonian H in Equation (4) has a chiral symmetry for h0 = 0:
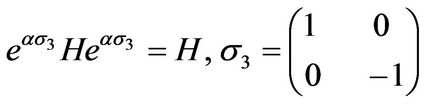 (10)
(10)
which connects eigenstates of energy −E with eigenstates of energy E by
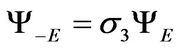 (11)
(11)
this is not the case after we have broken the chiral symmetry by the next-nearest-neighbor hopping term h0.
3. Dielectric Function
The longitudinal dielectric function in calculated in RPA [9,10]:
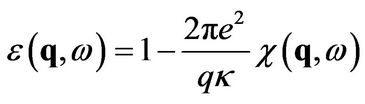 (12)
(12)
where κ is a dielectric constant and χ is a polarizability.
For polarizability we used the Lindhard formula [10], which in our case after some straightforward calculations can be reduced to the expression
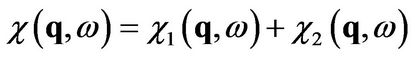 (13)
(13)
with the intraband contribution
 (14)
(14)
and the interband contribution
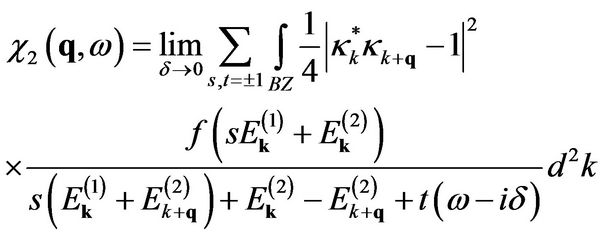 (15)
(15)

Figure 1. Energy dispersion of graphene with . The figure shows a broken particle-hole symmetry. The Dirac nodes are shifted up by
. The figure shows a broken particle-hole symmetry. The Dirac nodes are shifted up by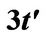 . The energy is measured in the units of the electronic bandwith (
. The energy is measured in the units of the electronic bandwith ( ).
).
where
 (16)
(16)
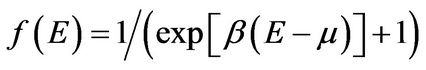 is the Fermi-Dirac distribution function,
is the Fermi-Dirac distribution function, 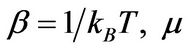 , is a chemical potential. The energies are defined as
, is a chemical potential. The energies are defined as
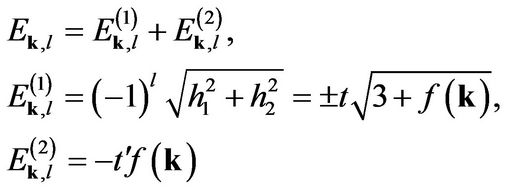 (17)
(17)
if we take 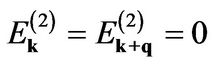 the integral yields the same polarizability formula as that found in the nearest-neighbor model’s polarizability [1,7].
the integral yields the same polarizability formula as that found in the nearest-neighbor model’s polarizability [1,7].
4. Plasmons in Graphene
In a first approximation, we can consider plasmons as collective excitations of electrons, where the dielectric function vanishes [8]:
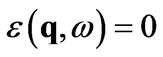 (18)
(18)
in general, however, the dielectric function is complex due to poles in the integrals (14) and (15). This implies that (18) has no solution, unless we only request that the real part of the dielectric function vanishes:
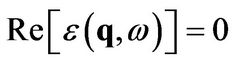 (19)
(19)
assuming a real function  as the plasmon dispersion.
as the plasmon dispersion.
For a numerical evaluation of the integrals it is more convenient to consider the loss function [6,8,10]
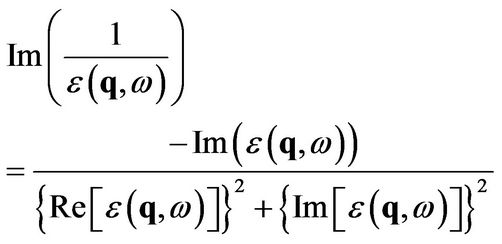 (20)
(20)
whose broadened peak indicates the plasmon. Here a complex solution 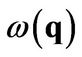 gives both the dispersion from the real part and the decay of the plasmons from the imaginary part.
gives both the dispersion from the real part and the decay of the plasmons from the imaginary part.
In the present paper the polarizability of grapheme χ is evaluated numerically and the corresponding dielectric function is obtained from Equation (12) for different values of the real frequency ω, the wave vector 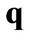 and chemical potential (Fermi energy) μ. Moreover, we assume κ = 4. The chemical potential level μ is selected to be relative to Dirac points whose existence is not affected by a variation of the parameter
and chemical potential (Fermi energy) μ. Moreover, we assume κ = 4. The chemical potential level μ is selected to be relative to Dirac points whose existence is not affected by a variation of the parameter 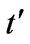 but are shifted by
but are shifted by 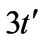 ([11]), as shown in Figure 2.
([11]), as shown in Figure 2.
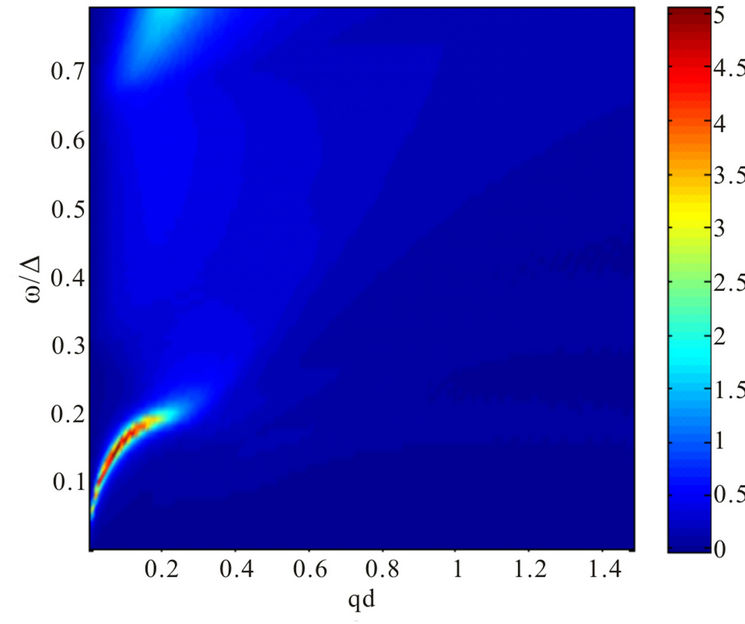
Our results for plasmon dispersion law are shown in Figures 3 and 4.
For each figure we have selected two values for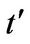 , namely
, namely 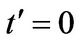 and
and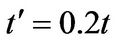 . The original chemical potentials μ that appear in Figures 3 and 4 are taken from the previous paper [1] and are modified by the value
. The original chemical potentials μ that appear in Figures 3 and 4 are taken from the previous paper [1] and are modified by the value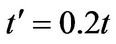 .
.
The influence of next-nearest hopping parameter 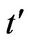 is insignificant for the plasmon dispersion law when the chemical potential is above Dirac point, as depicted in Figures 3 and 4. The shape of the plasmon dispersion law in Figure 3 does not change significantly by a varia-
is insignificant for the plasmon dispersion law when the chemical potential is above Dirac point, as depicted in Figures 3 and 4. The shape of the plasmon dispersion law in Figure 3 does not change significantly by a varia-
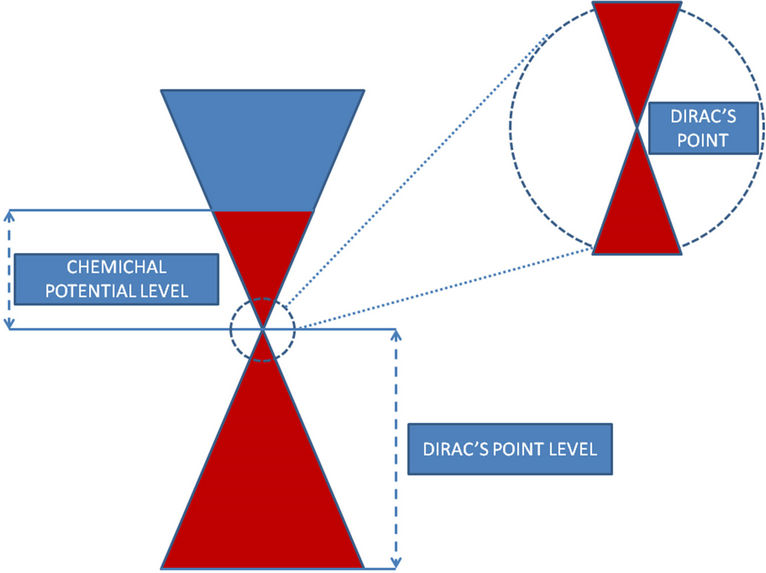
Figure 2. The scheme shows that chemical potential μ is taken relative to Dirac cone. Dirac point’s level is relative to case 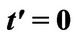 and the level equals to
and the level equals to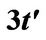 .
.
 (a)
(a)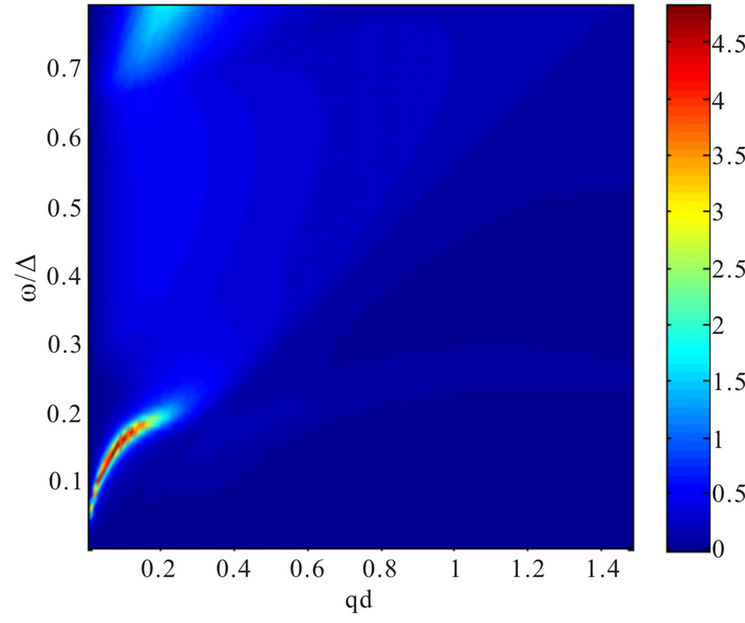 (b)
(b)
Figure 3. Plasmon dispersion for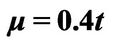 . (a) Plasmon dispersion for
. (a) Plasmon dispersion for ,
, 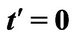 and different values of qy component (qx = 0); (b) Plasmon dispersion for
and different values of qy component (qx = 0); (b) Plasmon dispersion for ,
, 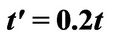 and different values of qy component (qx = 0).
and different values of qy component (qx = 0).
 (a)
(a) (b)
(b)
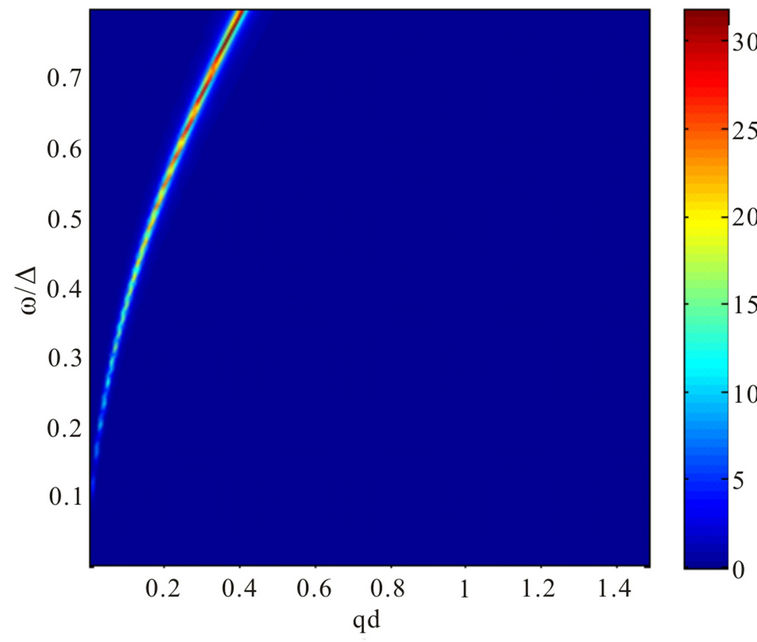
Figure 4. Plasmon dispersion for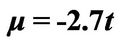 . (a) Plasmon dispersion for
. (a) Plasmon dispersion for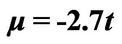 ,
, 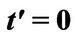 and different values of qy component (qx = 0); (b) Plasmon dispersion for
and different values of qy component (qx = 0); (b) Plasmon dispersion for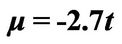 ,
, 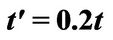 and different values of qy component (qx = 0).
and different values of qy component (qx = 0).
tion of the parameter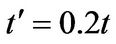 . On the other hand, the result is quite different when the chemical potential is below the Dirac point. Figure 4 shows that for different values of hopping parameter
. On the other hand, the result is quite different when the chemical potential is below the Dirac point. Figure 4 shows that for different values of hopping parameter 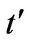 and for a negative chemical potential the shape of dispersion law changes strongly and the dispersion curve is much sharper when the value of the hopping parameter is larger. In general, our calculations of the plasmon dispersion law show that there is almost no change of the plasmon dispersion with
and for a negative chemical potential the shape of dispersion law changes strongly and the dispersion curve is much sharper when the value of the hopping parameter is larger. In general, our calculations of the plasmon dispersion law show that there is almost no change of the plasmon dispersion with 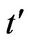 when chemical potential is above the Dirac point.
when chemical potential is above the Dirac point.
5. Conclusions
In conclusion we have investigated the 2D tight-binding hamiltonian model under the influence of the next nearest-neighbour coupling (constant) and we theoretically obtained analytic expression for improved graphene polarizability expression. Our work is extension to previous results obtained by [1] where only nearest-neighbor constant model is used. This work improves the previous results for graphene plasmon’s dispersion law.
The research of next-nearest hopping tight-binding model gave the possibility to investigate the plasmon’s dispersion law near Dirac point in the case of low values of chemical potential relative to Dirac point, by using analytical calculations and numerically to show that dispersion’s laws in two cases (nearest-neighbor and nextnearest tight binding model) are almost the same as predicted theoretically.
REFERENCES
- A. Hill, S. A. Mikhailov and K. Ziegler, “Dielectric Function and Plasmons in Graphene,” EPL (Europhysics Letters), Vol. 87, No. 2, 2009, Article ID: 27005.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, “The Electronic Properties of Grapheme,” Reviews of Modern Physics, Vol. 81, No. 1, 2009, pp. 109-162. doi:10.1103/RevModPhys.81.109
- D. S. L. Abergel, V. Apalkov, J. Berashevich, K. Ziegler and T. Chakraborty, “Properties of Graphene: A Theoretical Perspective,” Advances in Physics, Vol. 59, No. 4, 2010, pp. 261-482. doi:10.1080/00018732.2010.487978
- B. Wunsch, T. Stauber, F. Sols and F. Guinea, “Dynamical Polarization of Graphene at Finite Doping,” New Journal of Physics, Vol. 8, No. 12, 2006, p. 318.
- E. H. Hwang and S. Das Sarma, “Dielectric Function, Screening, and Plasmons in Two-Dimensional Graphene,” Physical Review B, Vol. 75, No. 20, 2007, Article ID: 205418. doi:10.1103/PhysRevB.75.205418
- M. Polini, R. Asgari, G. Borghi, Y. Barlas, T. PeregBarnea and A. H. MacDonald, “Plasmons and the Spectral Function of Grapheme,” Physical Review B, Vol. 77, No. 8, 2008, Article ID: 081411(R).
- S. J. Yuan, R. Roldan and M. I. Katsnelson, “Excitation Spectrum and High Energy Plasmons in Single-Layer and Multilayer Grapheme,” Physical Review B, Vol. 84, No. 3, 2011, Article ID: 035439.
- G. Mahan, “Many Particle Physics,” Plenum Pr., New York, 1990. doi:10.1007/978-1-4613-1469-1
- H. Ehrenreich and M. H. Cohen, “Self-Consistent Field Approach to the Many-Electron Problem,” Physical Review, Vol. 115, No. 4, 1959, pp. 786-790. doi:10.1103/PhysRev.115.786
- M. Dressel and G. Gruner, “Electrodynamics of Solids: Optical Properties of Electrons in Matter,” Cambridge University Press, Cambridge, 2002. doi:10.1017/CBO9780511606168
- P. R. Wallace, “The Band Theory of Graphite,” Physical Review, Vol. 71, No. 9, 1947, pp. 622-634. doi:10.1103/PhysRev.71.622

