Social Networking
Vol.04 No.04(2015), Article ID:60169,8 pages
10.4236/sn.2015.44012
The Effects of Centrality Ordering in Label Propagation for Community Detection
Brian Dickinson, Wei Hu
Department of Computer Science, Houghton College, Houghton, USA
Email: wei.hu@houghton.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 August 2015; accepted 6 October 2015; published 9 October 2015
ABSTRACT
In many cases randomness in community detection algorithms has been avoided due to issues with stability. Indeed replacing random ordering with centrality rankings has improved the performance of some techniques such as Label Propagation Algorithms. This study evaluates the effects of such orderings on the Speaker-listener Label Propagation Algorithm or SLPA, a modification of LPA which has already been stabilized through alternate means. This study demonstrates that in cases where stability has been achieved without eliminating randomness, the result of removing random ordering is over fitting and bias. The results of testing seven various measures of centrality in conjunction with SLPA across five social network graphs indicate that while certain measures outperform random orderings on certain graphs, random orderings have the highest overall accuracy. This is particularly true when strict orderings are used in each run. These results indicate that the more evenly distributed solution space which results from complete random ordering is more valuable than the more targeted search that results from centrality orderings.
Keywords:
Community Detection, Label Propagation, Centrality, Overlapping Community Detection

1. Introduction
Many real world systems and networks can be represented by graphs of edges and nodes. These systems include such diverse areas of study as social networks, html structure, and highway systems. One machine learning task which is often performed on these graphs is community detection in which algorithms attempt to find groups of nodes which have a significant difference in density between intragroup edges and intergroup edges, otherwise known as communities. These communities often provide some useful information about the elements represented by the nodes of a graph. For example communities in social network graphs likely define distinct social groups or subgroups. Similarly communities in an html graph might represent pages on the same domain or the same topic. A variety of techniques have been developed to find good communities in graphs; however, many of these methods are suitable only for finding discrete communities or communities with disjoint sets of nodes. This unfortunately is not how true communities form in many networks. In social networks, it is quite common for an individual or node to belong to multiple friend groups or communities. Similarly in a co-authorship network it would be expected that certain authors who are focused on interdisciplinary studies might belong in roughly equal parts to two or more of the communities for the disciplines in which he is involved. This problem has largely been addressed through modifications to existing discrete community detection algorithms.
One of the best known and simplest community detection algorithms is LPA or Label Propagation Algorithm [1] . Using this technique each node begins with a unique label. During each iteration, each node updates itself to the label which occurs most frequently amongst its neighbors choosing randomly among the most common if there is a tie. This continues until no labels are changed during an iteration. While this method produces surprisingly high accuracy its primary weaknesses are its lack of stability given that the ending condition may never be reached, and its inability to detect overlapping community structures. Both of these issues were corrected in SLPA or Speaker-listener Label Propagation Algorithm. SLPA keeps record of all of the labels it has received from its neighbors rather than simply the most recent label. This additional information allows for the detection of nodes with high belonging to multiple communities, as well as a change in termination requirements. Because the label received in each iteration is recorded, SLPA is able to run for a specified number of iterations without risking its detection results by terminating during a poor iteration. Despite its simplicity this algorithm has remained state of the art in overlapping community detection [2] .
It has been demonstrated that centrality functions can improve the community detection results of standard LPA. Therefore in this paper we combine SLPA with a variety of centrality functions on an assortment of networks with varied structures in order to determine the effects of centrality functions used in conjunction with SLPA. This study includes among others degree, betweenness, and closeness centrality functions. The community detection quality of SLPA for each centrality function and graph combination is given in Section 3.4. Prior to performing these tests however it was necessary to determine the convergence rate of SLPA on each of the chosen network graphs as SLPA unlike LPA requires input to determine the number of iterations of label propagation will be performed. These results are summarized in Section 3.1. The social networks, centrality functions and evaluation metrics used in this study are described in detail in the following section.
2. Data and Methods
2.1. Social Networks
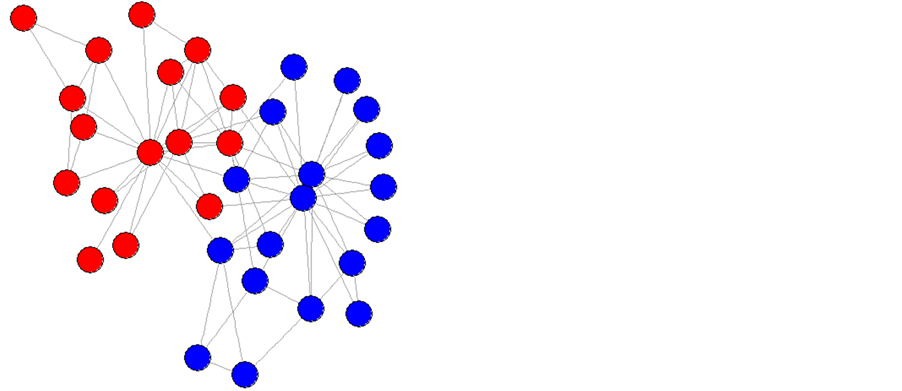
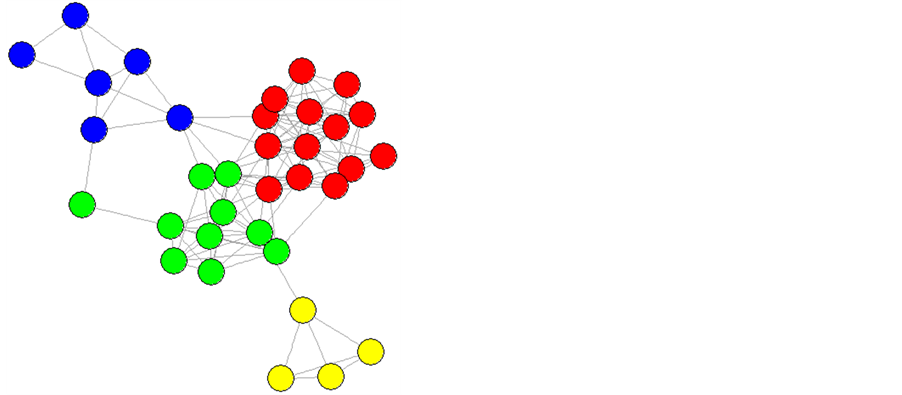
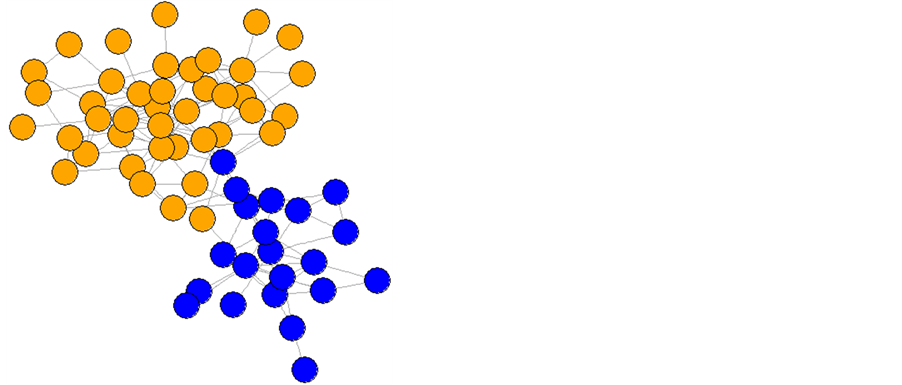
This study makes use of four social networks, karate, pilgrim, dolphins, and high school. Karate represents the social structure of a karate club from the 1970’s and is composed of thirty-four individuals and seventy-eight connections; it is perhaps the most commonly referenced social network [3] (Figure 1). The pilgrim network represents the friendships of a high school senior class. It contains thirty-four nodes, one-hundred twenty-eight edges, and an assortment of community types from densely interconnected communities and cliques, to a sparse fringe community [4] (Figure 2). The dolphins graph is a social interaction graph representing contact time between dolphins within a pod off the coast of New Zealand. It is made up of sixty-two nodes and one-hundred fifty-nine edges [5] (Figure 3). Finally the largest network used in this study was high school with sixty-nine nodes and two-hundred eighteen edges. This network represents a large body of students at a single high school ranging from seventh to twelfth grade [2] (Figure 4). These networks were selected for their diversity in structure and for their small size. Diversity should prevent result bias towards certain graph structures, while a small size will allow repeated testing to account for random variance in the results of label propagation.
2.2. Centrality Functions
In order to evaluate the benefits of applying centrality to the ordering of nodes for propagation, seven different centrality functions were selected. These include degree centrality, subgraph centrality, closeness centrality, betweenness centrality, alpha centrality, leadership quality, and Page Rank. Degree centrality was the first and simplest measure of centrality. In undirected graphs such as those used in this study, the centrality of a node is merely its degree. Subgraph centrality is based on the number and size of all closed walks within the graph that contain each node [6] . Similarly closeness centrality is based on the number of steps required to access every other node from each node [7] . Betweenness centrality on the other hand evaluates nodes based on the number
Figure 1. Karate social network.
Figure 2. Pilgrim high school network.
Figure 3. Dolphins interaction network.
Figure 4. High school network.
of shortest paths passing through them [8] . Leadership quality introduced by B. Valyou et al. in [9] weights nodes based on their aggregate neighborhood similarity with each node in their neighborhood. Alpha centrality is a modification of the eigenvector centrality function which weights nodes based on their degree and the degree of their neighbors [10] . Finally PageRank is a variant of eigenvector centrality which weights connections in a slightly different way [11] . Each of these centrality functions rate the centrality of each node differently and as a result will often result in different orderings for the purpose of ordering nodes for label propagation.
2.3. Speaker-Listener Label Propagation Algorithm
In the original Label Propagation Algorithm (LPA), each node is initially assigned a unique label. During each iteration each node is visited in a random order, and when visited assigns itself the label most common amongst its neighbors. In the case of a tie one label is selected randomly from the set of maximal labels. This process continues until each node’s label is a most common label amongst its neighbors. Each node is then assigned to a community based on the label it currently has after the final iteration. This technique is very effective for its simplicity; unfortunately however it can produce disconnected communities and is rather unstable due to its uncertain termination condition.
The Speaker-Listener Label Propagation Algorithm or SLPA is an extension of the standard label propagation algorithm which attempts to imitate the natural process of human communication for information dissemination [1] . Like LPA, SLPA begins by assigning each node a unique label. Similarly at each iteration every node is visited in a random order. When visited however, rather than simply accepting the maximal label amongst neighbors, the node polls its neighbors for labels. Each neighboring node then randomly selects one label it has previously received with proportional probability to the number of times it has been received. The listening node then chooses the most common label from these received labels. Again in the case of a tie one label is selected randomly from the maximal set of received labels. This algorithm is summarized in Figure 5. The process of maintaining a list or table of received labels instead of simply the most recent label greatly stabilizes the results of SLPA. It also removes the necessity of LPA’s uncertain termination condition and instead substitutes a simple parameter for the number of iterations which should be completed. This is made possible by the method for assigning nodes to communities after propagation is completed. Since a count for the number of labels received is available, nodes may either be assigned to the most common community in their collection of received labels, or may be assigned to multiple communities based on a percentage of labels received threshold. In either case generally very few iterations are needed to reach optimal community detection. SLPA is then a stabilized version of LPA which has been adapted to find overlapping community structures. It was selected for its stabilization since the goal of this study is to evaluate the effects of centrality ordering on label propagation in cases where the algorithm does not need to be stabilized. It has already been demonstrated that centrality ordering can increase stability; however there are no indications of its other effects on community detection quality [12] .
Figure 5. SLPA pseudo-code.
Ordering nodes according to centrality was performed as a two-step process. First centrality values were calculated for each node using a selected centrality function. Then nodes were selected for ordering with probability proportional to their centrality value. This resulted in high centrality nodes appearing more frequently early in the ordering and low centrality nodes usually occurring later in the ordering while still maintaining some level of randomness. The second step of this process was repeated at each iteration resulting in a new ordering each time.
2.4. Community Quality Metrics
There are several ways to measure the quality of detected communities in a graph. By far the most popular methods for this task on discrete community partitions are normalized mutual information and modularity. Modularity evaluates the goodness of a community structure by looking at intercommunity edges and intracommunity edges within a graph [13] . Normalized mutual information on the other hand compares the community vector of the algorithm’s partitioning with a known ground truth partitioning of the network [14] . A few different adaptations of modularity have been suggested for measuring the goodness of overlapping communities. For this study we will adopt the Modularity EQ method formula presented by Shen et al. [15] . Each of these metrics has a slightly different method of measuring different facets of the goodness of a community partitioning and will provide full insight to the quality of communities generated by our algorithms.
3. Results
All testing was done a collection of identical machines operating Linux Mint 17. For the purpose of this study the clock speed and available RAM of these machines is irrelevant as convergence and efficiency are measured in number of runs and number of iteration per run while all processing takes place on the JVM version 1.7.0_79. SLPA was implemented in Java and received centrality values from the built in centrality functions included in the igraph package of R. Random number generation was handled by the native SecureRandom package of Java.
3.1. Convergence Rates of SLPA Using Different Centrality Metrics
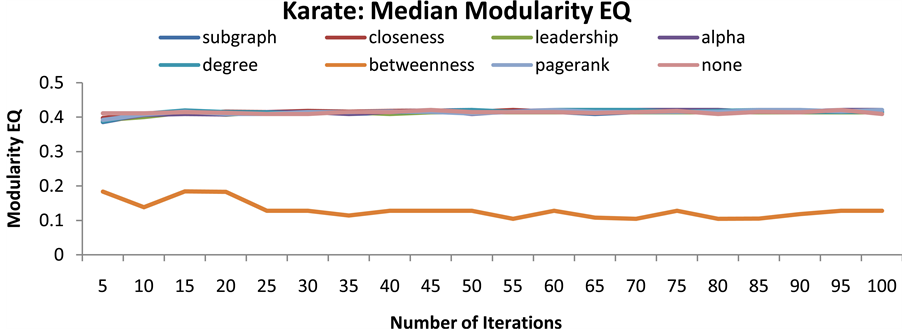
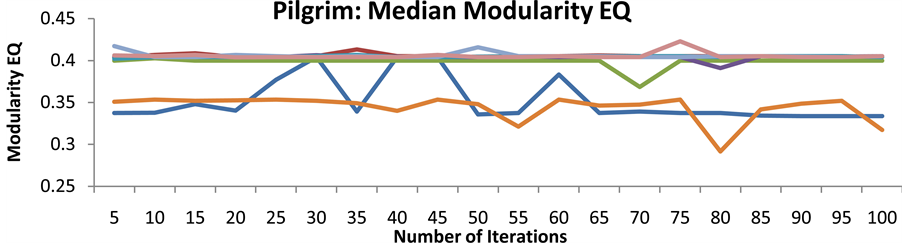
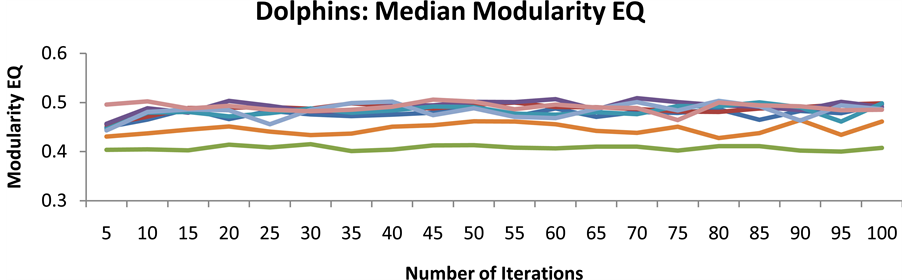
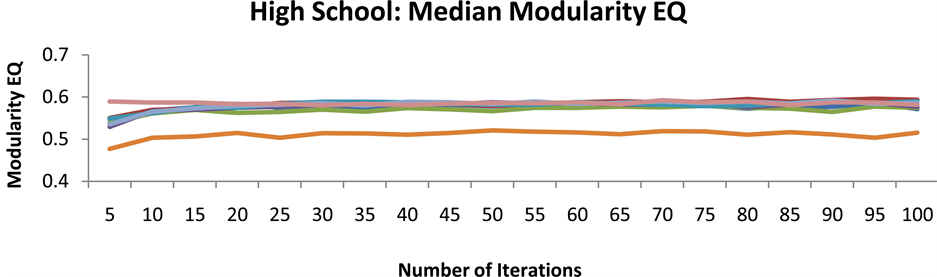
In order to determine how quickly SLPA converged on an accurate community partition for each graph, SLPA was run with a varying iterations parameter from five to one-hundred. SLPA was run twenty-five times at each number of iterations, and the median value was kept to better gauge how an average run at that iteration count would perform. This was repeated for each of the seven centrality functions, each time ordering nodes for label propagation based on their ranking from the selected centrality function using the process described in the previous section. The median overlapping modularity value on every graph for each number of iterations and centrality function are shown in Figures 6-9. It is clear although perhaps surprising that on these small networks convergence occurs for most algorithms after only five or ten iterations. For this reason all subsequent accuracy tests were run with only twenty-five iterations to minimize runtime without compromising accuracy.
3.2. Community Partitioning Quality of SLPA Using Various Centrality Measures
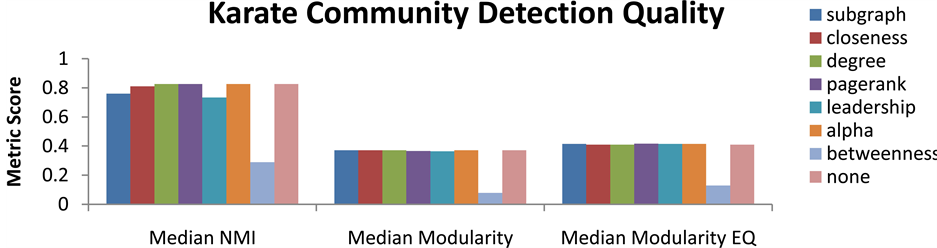
Each centrality function was used in running SLPA one-hundred times on each graph. The results of these runs were recorded and evaluated based on three metrics: normalized mutual information, modularity, and overlap
Figure 6. Median overlapping modularity value of SLPA on the karate network with different iteration parameters.
Figure 7. Median overlapping modularity value of SLPA on the pilgrim network with different iteration parameters.
Figure 8. Median overlappingmodularity value of SLPA on the dolphin network with different iteration parameters
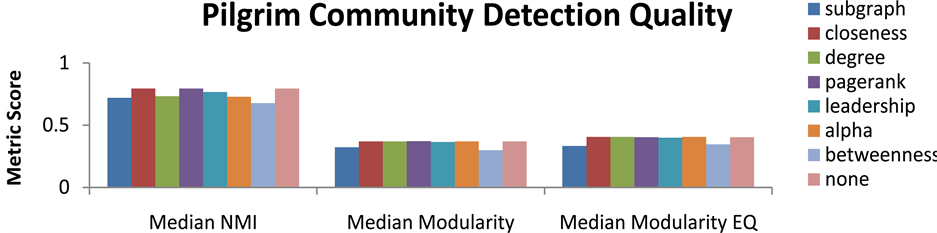
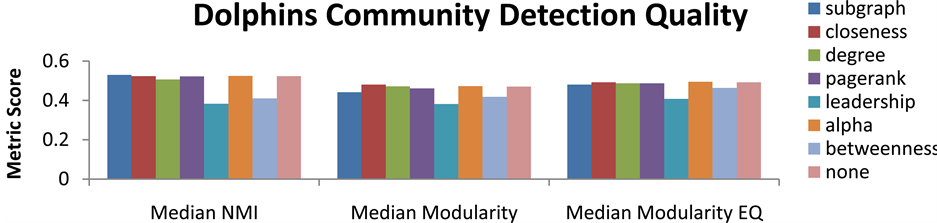
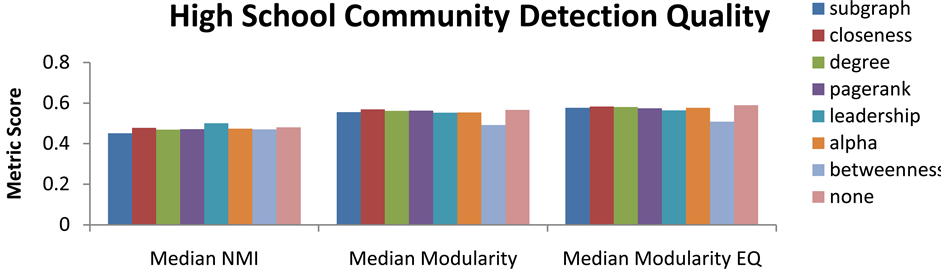
modularity. The median value for each of these metrics was selected and presented in Figures 9-13 to provide a clear picture of the average performance of SLPA using each centrality function. It is quickly apparent that few of the centrality functions have a significant effect on community detection quality. In fact the only clearly significant centrality function is betweenness which drastically reduces the quality of community partitions. This is likely due to this functions emphasis on shortest paths which will cause it to identify bridge nodes between communities. If these nodes are allowed to propagate first it can result in labels flowing between communities more easily than they might otherwise. This likely is the cause of merging communities and poor community structure in these runs of SLPA. Several other functions regularly outperformed random ordering on some graphs and underperformed on others. This may indicate that different centrality functions are more valuable on certain graphs. This may be a sign of over fitting results towards a subset of graphs with certain characteristics. For this reason it appears that completely random ordering is optimal for SLPA since its more evenly distributed solution space can account for all possible graph structures.
Figure 9. Median overlapping modularity value of SLPA on the high school network with different iteration parameters.
Figure 10. Community partition quality for karate by centrality function used for ordering label propagation in SLPA.
Figure 11. Community partition quality for pilgrim by centrality function used for ordering label propagation in SLPA.
Figure 12. Community partition quality for dolphins by centrality function used for ordering label propagation in SLPA.
4. Conclusions
The results of this testing show that for a variety of label propagations which have already been stabilized, ordering nodes for label propagation based on centrality functions do not improve predictive quality. In fact in most cases it slightly decreases performance when compared across a variety of different social network structures.
Figure 13. Community partition quality for high school by centrality function used for ordering label propagation in SLPA.
This is especially true of betweenness centrality which significantly reduces performance in almost all cases. The reason for this becomes quite apparent when one considers how reordering can effect community detection. Since betweenness has a tendency to give priority to bridge nodes which border multiple communities, allowing these nodes to propagate first increases the chances of a label overflowing its community bounds skewing propagation results. Other centrality functions may also cause this bias on certain graphs where bridge nodes have other qualities such as high degree or closeness centrality. This demonstrates that the primary value of ordering label propagation based on centrality is in its stabilizing effect; however, other methods such as those employed by SLPA may prove more effective since they do not as a consequence negatively affect community partitioning. For this reason we assert that in the case of SLPA random node ordering is the optimal ordering when testing across different graph structures.
Further research in this topic could focus on the application of centrality functions to other versions of label propagation which have not yet produced stable termination. Centrality based order has already demonstrated that it can have a stabilizing effect on standard label propagation and this study demonstrates that centrality ordering has little or no negative effect on final community detection. Centrality ordering therefore could enhance the stability of other label propagation algorithms without reducing the effectiveness of their clustering.
Acknowledgements
We would like to thank the Summer Research Institute at Houghton College for providing us with this research opportunity.
Cite this paper
BrianDickinson,WeiHu, (2015) The Effects of Centrality Ordering in Label Propagation for Community Detection. Social Networking,04,103-111. doi: 10.4236/sn.2015.44012
References
- 1. Xie, J., Szymanski, B.K. and Liu, X. (2011) SLPA: Uncovering Overlapping Communities in Social Networks via a Speaker-Listener Interaction Dynamic Process. Proceedings of Data Mining Technologies for Computational Collective Intelligence Workshop at ICDM, Vancouver, 11 December 2011, 344-349. http://dx.doi.org/10.1109/icdmw.2011.154
- 2. Xie, J., Kelley, S. and Szymanski, B. (2013) Overlapping Community Detection in Networks: The State of the Art and Comparative Study. ACM Computing Surveys, 45, 1-35. http://dx.doi.org/10.1145/2501654.2501657
- 3. Zachary, W.W. (1977) An Information Flow Model for Conflict and Fission in Small Groups. Journal of Anthropological Research, 33, 452-473.
- 4. Dickinson, B., Valyou, B. and Hu, W. (2013) A Genetic Algorithm for Identifying Overlapping Communities in Social Networks Using an Optimized Search Space. Social Networking, 2, 193-201. http://dx.doi.org/10.4236/sn.2013.24019
- 5. Lusseau, D., et al. (2003) The Bottlenose Dolphin Community of Doubtful Sound Features a Large Proportion of Long-Lasting Associations—Can Geographic Isolation Explain This Unique Trait? Behavioral Ecology and Sociobiology, 54, 396-405. http://dx.doi.org/10.1007/s00265-003-0651-y
- 6. Estrada, E. and Rodriguez-Velazquez, J.A. (2005) Subgraph Centrality in Complex Networks. Physical Review, 71, Article ID: 056103. http://dx.doi.org/10.1103/physreve.71.056103
- 7. Freeman, L.C. (1979) Centrality in Social Networks I: Conceptual Clarification. Social Networks, 1, 215-239. http://dx.doi.org/10.1016/0378-8733(78)90021-7
- 8. Brandes, U. (2001) A Faster Algorithm for Betweenness Centrality. Journal of Mathematical Sociology, 25, 163-177. http://dx.doi.org/10.1080/0022250X.2001.9990249
- 9. Valyou, B., Dickinson, B. and Hu, W. (2014) Determining Leaders and Communities on Networks Using Neighborhood Similarity. Social Networking, 3, 50-57. http://dx.doi.org/10.4236/sn.2014.31006
- 10. Bonacich, P. and Paulette, L. (2001) Eigenvector-Like Measures of Centrality for Asymmetric Relations. Social Networks, 23, 191-201. http://dx.doi.org/10.1016/S0378-8733(01)00038-7
- 11. Brin, S. and Page, L. (1998) The Anatomy of a Large-Scale Hypertextual Web Search Engine. Proceedings of the 7th World-Wide Web Conference, Brisbane, April 1998. http://dx.doi.org/10.1016/s0169-7552(98)00110-x
- 12. Xing, Y. (2014) A Node Influence Based Label Propagation Algorithm for Community Detection in Networks. The Scientific World Journal, 2014, Article ID: 627581. http://dx.doi.org/10.1155/2014/627581
- 13. Newman, M.E.J. (2004) Finding and Evaluating Community Structure in Networks. Physical Review E, 69, Article ID: 026113. http://dx.doi.org/10.1103/physreve.69.026113
- 14. Danon, L., Diaz-Guilera, A., Duch, J. and Arenas, A. (2005) Comparing Community Structure Identification. Journal of Statistical Mechanics: Theory and Experiment, 9, Article ID: P09008. http://dx.doi.org/10.1088/1742-5468/2005/09/p09008
- 15. Shen, H., Cheng, X., Cai, K. and Hu, M.B. (2009) Detect Overlapping and Hierarchical Community Structure in Networks. Physica A, 388, 1706-1712. http://dx.doi.org/10.1016/j.physa.2008.12.021