Social Networking
Vol.2 No.3(2013), Article ID:33943,39 pages DOI:10.4236/sn.2013.23011
Who Is Collaborating with Whom in Science? Explanation of a Fundamental Principle
1WISELAB, Dalian University of Technology, Dalian, China 2COLLNET Center, Hohen Neuendorf, Germany
Email: kretschmer.h@onlinehome.de
Copyright © 2013 Hildrun Kretschmer, Theo Kretschmer. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 8, 2.13; revised June 7, 2013; accepted July 3, 2013
Keywords: Social Network Analysis (SNA); Collaboration; Co-Authorship; Mathematical Model
ABSTRACT
Since many decades power functions are well-known in counting single scientists or co-author pairs in social networks. However, in this paper a developed procedure for visualizing a bivariate distribution of co-author pairs’ frequencies hence producing three-dimensional graphs is presented. This distribution is explained by a fundamental principle of social group formation and described by a mathematical model. This model is applied to 52 co-authorship networks. For 96% of them the squared multiple R is larger than 0.98 and for 77% of the 52 networks even larger than 0.99. The visualized social Gestalts in form of three-dimensional graphs are rather identically with the corresponding empirical distributions. Question: Can we expect a general validity of this mathematical model for co-authorship networks?
1. Introduction
What does it mean: “Fundamental Principles of Social Group Formations?” There are both visible formations and non-visible. The visualization of a special non-visible fundamental principle of social group formations in co-authorship networks is presented in our paper. In this connection a mathematical model for the intensity function of interpersonal attraction (Social Gestalt) will be explained.
1.1. Fundamental Principles of Social Group Formations (Visible and Non-Visible)
Already in the prehistoric times of higher vertebrates— birds and mammals—several fundamental principles of well-ordered social group formations had existed and some of them are also identifiable in humans. For example, group formations of fishes or birds are well-known. These kinds of group formations can be observed by our own eyes (cf. Figures 1 and 2). The shapes of these group formations can be changed depending on the changing environment (cf. Figure 2).
However, well-ordered social group formations in coauthorship networks are non-visible formations and have to become visualized by special methods. Changing shapes are presented and explained by a mathematical

Figure 1. Group formation of fishes (the picture is a copy from Wikipedia).
model for the intensity function of interpersonal attraction (Social Gestalt), example, cf. Figure 3. In the present paper we are looking for a well-known fundamental principle of social group formations (social Gestalts).
We have created methods for visualization of the cor- responding well-ordered social Gestalts, i.e. they are well-ordered like the shown shapes above with changing shapes in dependence on both the changing environment

Figure 2. Changing shape of group formation (the picture is a copy from Wikipedia).
and/or scientists. Result: We have visualized social Gestalts in co-authorship networks concerning the question: Who is collaborating with whom in science?
1.2. Brief Literature Review: Who Is Collaborating with Whom in Science?
There is a rapid increase of cooperation in science since many decades. This has led to an increase in the number of scientific studies of this topic internationally [1,2].
A high diversity of studies regarding the question “Who is collaborating with whom” can be found in the literature. A few of them should be mentioned here:
• On the level of cross-national collaboration Glänzel & Schubert [3] have presented the cross-national preference structure of 36 selected countries. The study revealed that geopolitical location, cultural relations and language are determining factors in shaping preferences in co-authorship.
• Liang & Zhu [4] obtained for inter-regional co-operation in China that geographical proximity is an important factor. Nagpaul [5] studied international research collaboration and concluded that geographical proximity has greater positive impact on the preference in collaboration than thematic proximity and socio-economic proximity. Geographical proximity is also studied by Have-mann, Heinz & Kretschmer [6] and by Katz [7].
• On the individual level Braun, Schubert & Glänzel [8] have described the features of productivity and copublication patterns of four types of authors. For this purpose, the authors were classified according to their anterior and posterior records. The collaboration pattern between the four types was studied.
The above mentioned studies are important in general and of special interest for science and technology policy. Additionally, other approaches in the field of collaboration studies are coming from the informetric point of view and are related to mathematical modelling of collaboration networks.
Egghe’s paper [9] has given a model for the size-frequency function of co-author pairs. Starting with the well-know Lotka’s Law [10] Egghe has emphasized [9]; another way of looking at author production is by studying co-author pairs and the number of their joint papers. According to Egghe’s opinion this topic is becoming more and more important since collaboration increases in time.
Egghe has referred to both Morris and Goldstein’s [11] approach regarding univariate distributions and Kretschmer & Kretschmer’s approach [12] regarding a bivariate distribution, hence producing three-dimensional graphs.
Univariate distribution means, counting authors as in Lotka’s distribution is replaced by counting co-author pairs, but hence also producing two-dimensional graphs similar to Lotka’s distribution.
Whereas the univariate approaches by Egghe [9] and by Morris & Goldstein [11] don’t include the aspect: “Who is collaborating with whom”, Kretschmer & Kretschmer’s [12] bivariate distribution is focused on this question: Is there any fundamental principle existing regarding the preference in collaboration between individual authors?
• 1.3. Hypotheses
• In dependence on the productivities of collaborators —a special fundamental principle of social group formation is a determining factor in shaping preferences in co-authorship between individual scientists.
• The corresponding well-ordered distributions of coauthor pairs’ frequencies and changing shapes of these distributions (Example, cf. Figure 3) can be described by a mathematical model.
2. Theoretical Approach
On this place a brief introduction of the used methods is necessary for further explanations of the theoretical approach. The extended version regarding the methods can be found in Appendix.
2.1. Brief Introduction of the Used Methods
The number of publications 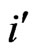 per author P is determined by resorting to the “normal count procedure”. Each time the name of an author appears, it is counted. The co-author pairs P, Q are counted under the condition of both the first authors P count
per author P is determined by resorting to the “normal count procedure”. Each time the name of an author appears, it is counted. The co-author pairs P, Q are counted under the condition of both the first authors P count  and the second authors Q count
and the second authors Q count . A bivariate distribution of co-author pairs’ frequencies
. A bivariate distribution of co-author pairs’ frequencies 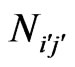 is studied hence producing three-dimensional graphs. Under the condition the place of P or Q in the by-line is not considered, a symmetrical matrix and following a symmetrical graph is
is studied hence producing three-dimensional graphs. Under the condition the place of P or Q in the by-line is not considered, a symmetrical matrix and following a symmetrical graph is

Figure 3. Example: Change of the shapes of the well-ordered distribution of co-author pairs’ frequencies over time (Journal of Experimental Medicine. First and second rows: Pattern based on data from one year: 1980. Third and fourth rows: Pattern based on data from 19 years: 1980-1998). The patterns on the left (both first and third rows) are turned around three times each.
resulting (Example, cf. Table 1).
Distributions of this kind of co-author pairs’ frequencies are already published [12-15].
However, these distributions were restricted to
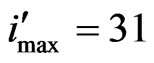 .
.
Usually the stochastic noise is increasing with higher productivity because of the decreasing number of authors. We intend to overcome these problems in this paper with help of the logarithmic binning procedure. Newman has already proposed in 2005 [16] to use the logarithmic binning procedure for the log-log scale plot of power functions. To get a good fit of a straight line (log-log scale plot of power functions, for example Lotka’s distribution), we need to bin the data  into exponential wider bins. Each bin is a fixed multiple wider than the one before it. For example, choosing the multiplier of 2 we receive the intervals 1 to 2, 2 to 4, 4 to 8, 8 to 16, etc.···, i.e. the sizes or widths of the bins
into exponential wider bins. Each bin is a fixed multiple wider than the one before it. For example, choosing the multiplier of 2 we receive the intervals 1 to 2, 2 to 4, 4 to 8, 8 to 16, etc.···, i.e. the sizes or widths of the bins 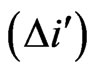 are 1, 2, 4, 8, etc.··· The number of samples in a bin should be divided by the width of this bin to get a count per unit interval of
are 1, 2, 4, 8, etc.··· The number of samples in a bin should be divided by the width of this bin to get a count per unit interval of . In other words, the new value in a bin i is simply the arithmetic average of all the points in the bin. The sequence of the bins i is i (i = 1, 2, 4, 8, 16, 32, 64, 128, 256···). The same holds for the sequence of the bins j.
. In other words, the new value in a bin i is simply the arithmetic average of all the points in the bin. The sequence of the bins i is i (i = 1, 2, 4, 8, 16, 32, 64, 128, 256···). The same holds for the sequence of the bins j.
We have extended this procedure for use in bivariate distributions (Details cf. Appendix. The width of a bin (cellij) in the matrix is the product of ∆i and ∆j: (∆i × ∆j).
The number of co-author pairs in a bin (cellij) has to be divided by the width of the bin: (∆i × ∆j). The result is the arithmetic average of all the points in this bin.
Using the log-log-log presentation after the logarithmic binning procedure, we are starting in this paper with the following kind of matrix (cf. Table 2) as basis for three-dimensional graphs. The sequence of log i (rows) is as follows: log i (log i = 0, 0.301, 0.602, 0.903, 1.204, 1.505, 1.806, 2.107, 2.408), the same is hold for log j (columns). The main diagonal of a square matrix is the diagonal which runs from the top left corner to the bottom right corner with:
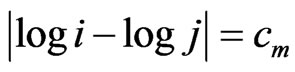 (1)
(1)
The secondary diagonal is the diagonal of a square matrix running from the lower left entry to the upper right entry with:
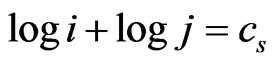 (2)
(2)
cm and cs are constants.
Visualization of the Social Gestalts:
For visualization of the theoretical patterns (Social Gestalts) the Function Plot of SYSTAT is used and the Scatterplot for the empirical patterns. (The detailed procedure for visualizing the empirical data of the distribution of co-author pairs’ frequencies in comparison

Table 1. Example of an artificial symmetrical matrix of the co-author pairs’ frequencies Ni'j' = f(i',j').
with the theoretical Gestalt can be found in Appendix (Heading 5)). An example for the predictions for the places of the empirical values in the theoretical pattern (Social Gestalts) is shown in Figure 4 as well as the overlay of the corresponding empirical data. The lines of the theoretical patterns are obtained by the mathematical model (Figure 4, first row, left pattern). The points, two of the lines touch each other, are the predictions for the places of the empirical values. After overlay of the social Gestalt (cf. left pattern, first row: Theoretical Model) and the empirical distribution (cf. right pattern, first row: Empirical Data) into a single frame (Pattern in the second row) the goodness-of-fit is highest in case the empirical values are placed directly on these points obtained from the theoretical Gestalt.
Regarding the three-dimensional graphs we assume the fundamental principle of social group formations is one of the determining factors in shaping preferences in co-authorship between individual scientists (cf. 1.3. Hypotheses). Therefore we have applied the corresponding mathematical model for describing co-author pairs’ frequencies [12]. This model is presented in Section 2.2 “Model for the Intensity Function of Interpersonal Attraction (Social Gestalt)”.
Complementarities are a crucial determinant of this model. In conjunction with these complementarities, various shapes of the distribution of observed co-author pairs’ frequencies emerge. Two contrary of them (convex and concave) are selected for presentation in Figure 5.

Table 2. Square matrix of co-author pairs (logNij). Note: The main diagonal is green colored and the secondary diagonal red.

Figure 4. Overlay of the empirical data and the theoretical model.
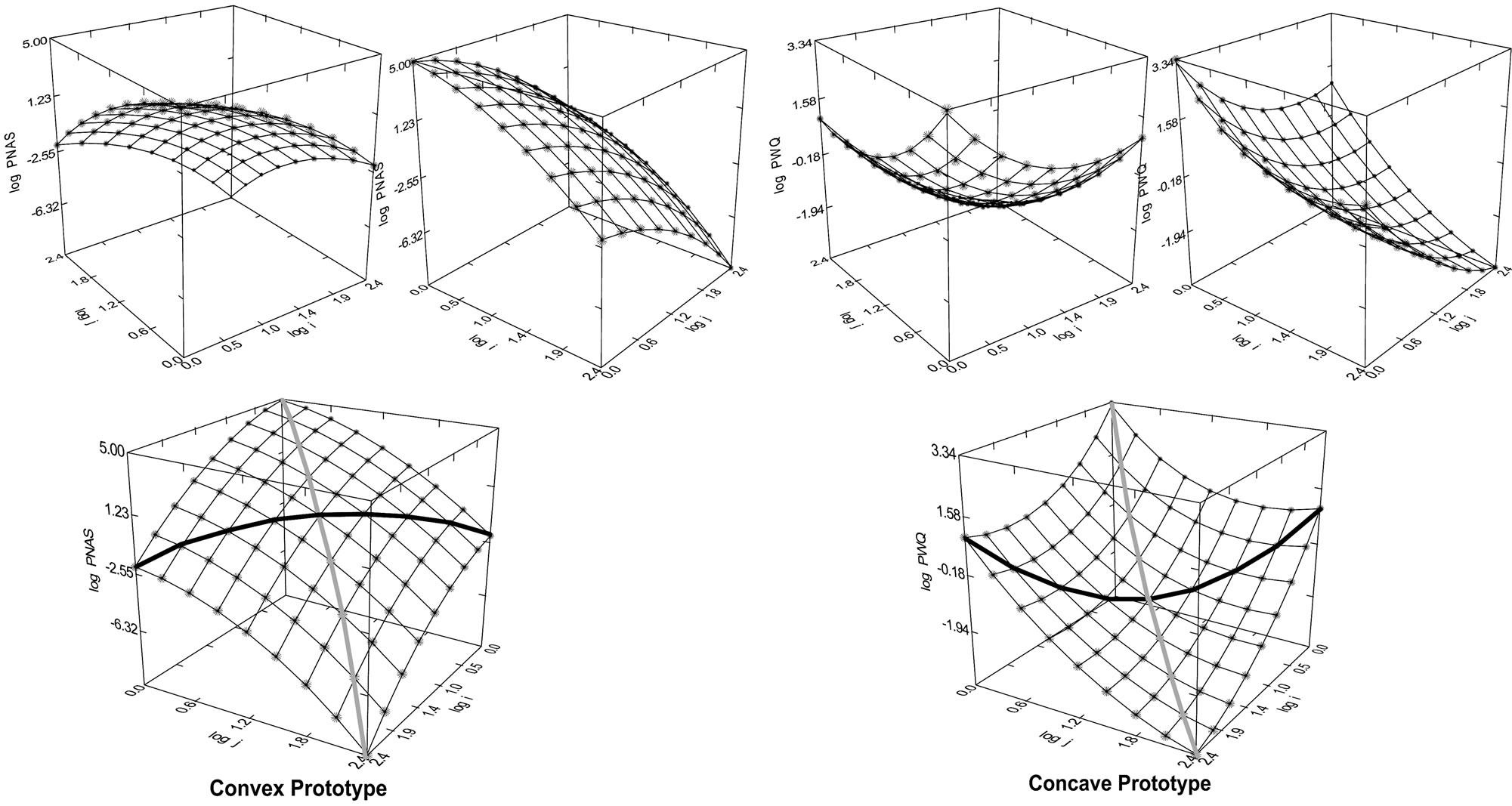
Figure 5. Two prototypes of distributions of co-author pairs’ frequencies with opposite shapes (Convex and concave). Patterns on the second row: The values on the third dimension (logNij) related to the main diagonals (cf. Table 2) are green coloured and the values related to the secondary diagonals (cf. Table 2) are red. The left prototype shows a convex shape and the right a concave. Each prototype is turned around two times. The prototypes are theoretical models.
The comparison between the curvilinear lines (red and green) in Figure 5 (convex and concave) is also shown in two-dimensional graphs (Figure 6). The two-dimensional graphs are used for explanation of the model in Section 2.2.
2.2. Model for the Intensity Function of Interpersonal Attraction: Social Gestalt
(Partially presented in [12]).
2.2.1. General Remarks
Interpersonal attraction is a major area of study in social psychology. Whereas in physics, attraction may refer to gravity or to the electro-magnetic force, interpersonal attraction can be thought of force acting between two people tending to draw them together. To achieve predictive accuracy, one must refer to the qualities of the attracted as well as the qualities of the attractor when measuring interpersonal attraction. Qualities maybe for example, terms of age or of productivity. It is suggested that to determine attraction, personality and situation (or environment) must be taken into account. The notion of “birds of a feather flock together” points out that similarity of quality is a crucial determinant of interpersonal attraction. Do birds of a feather flock together, or the opposites attract? This leads to a model of complementarities.
The modern notion of complementarities introduced by Niels Bohr had existed already in a clear-cut manner in old Chinese thought, in the Yin/Yang teaching. Yin and Yang have to be seen as polar forces of only one whole, as complementary tendencies interacting dynamically with each other, so that the entire system is kept flexible and open to change (For example, expressed in varying shapes of the social Gestalt).
Based on this background Kretschmer [17,18] has already created a model for social Gestalts valid for social networks in general. This model is also applied for description of the distribution of co-author pairs’ frequencies Nij [12]. The present paper shows a special extension by logarithmic binning procedure.
The fundamental “formula” of Gestalt theory might be expressed in this way: there is a whole, the behaviour of which is not determined by that of their individual elements, but where the part-processes are themselves determined by the intrinsic nature of the whole [19]. Holistic organizational patterns playing a role that comprised man and the environment. These holistic entities are often designated as psychological fields. Their tendency towards a stable state of order is called conciseness (or “Prägnanz”) tendency, it is a “tendency towards a good Gestalt”. The stable final state is, if possible, built up in a simple, well-ordered, harmonic and uniform manner in line with definite rules. Several authors take the view that these fields can be mathematically described.
With this in mind, the distribution of observed co-au-

Figure 6. The curvilinear lines related to the diagonals in Figure 5 (red and green) are shown here in two-dimensional graphs. Straight lines are added to the patterns in the first and second columns for comparison. The upper two patterns show the curvilinear lines attached to the main diagonal (left: convex, right concave) and the lower two patterns to the secondary diagonal (left: convex, right concave). The corresponding standardized versions of the last can be found on the right side. The upper two patterns on the left side are rather equal to the standardized versions. The two-dimensional graphs are used for explanation of the model in Section 2.2.
thor pairs’ frequencies can be considered to be a special reflection of a social Gestalt.
The model of social Gestalts mathematically describes, and textual explains, well-ordered fields of mutual attraction between a large numbers of individual persons. In conformity with complementarities or Yin/Yang theory these fields change their shapes depending on changing personalities and/or situations.
In brief:
Holistic entities with balancing interactions of forces are considered both by Gestalt psychology and Yin/Yang teaching.
• The “tendency towards a good Gestalt” is a special feature of the Gestalt psychology.
• The complementarities are a special feature of the Yin/Yang theory.
In conclusion, the social Gestalt is a model that comprised the “tendency towards a good Gestalt” but the definite rules are obtained by considering the complementarities.
The model is based on two independent different Yin/Yang pairs:
• The first Yin/Yang pair is connected with the secondary diagonal and its parallels (cf. Table 2), with the complementary poles: Similarities of attractors’ qualities (called “Yang” as metaphor) Dissimilarities of attractors’ qualities (called “Yin”).
• The second Yin/Yang pair is connected with the main diagonal and its parallels, with the complementary poles: high average level of attractors’ qualities (called “Yang”) low average level of attractors’ qualities (called “Yin”) “Independent Yin/Yang pairs” means, the complementary tendencies of one Yin/ Yang pair are interacting dynamically with each other independently from the complementary tendencies of the other Yin/Yang pair.
A special function is defined for each of the Yin/Yang pairs: ZA for the first pair and ZB for the second.
Because of independence we assume the intensity of mutual attraction ZXY is proportional to the product of the two functions ZA and ZB:
 (3)
(3)
In detail: We assume the intensity structure of mutual attraction ZXY can be described by a function of a special power functions’ combination (X is the value of a special personality characteristic (or quality) of an attracted and Y is the value of the same personality characteristic (or quality) of the attractor and in case of mutual attraction also vice versa).
Whereas the empirical shapes of power law distributions are rather similar with each other the empirical shapes of the three dimensional distributions show manifold shapes.
2.2.2. Function ZA for the Description of the First Yin/Yang Pair
The function ZA is a combination of two special power functions:
The crucial determinant of interpersonal attraction (similarity or dissimilarity respectively) suggests to consider the distances A between the qualities of persons 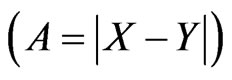 as independent variable of a power function:
as independent variable of a power function:
First power function:
 (4)
(4)
c1 = constant
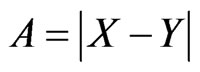 (5)
(5)
The 1 is added because logA is not possible in case A = 0.
A power function with only one parameter (unequal to zero) is either only a monotonically declining or only a monotonically rising function, when referred to both proverbs: either “Yin” or “Yang” (Figure 7).
In order to fulfil the inherent requirement that both proverbs with their extensions can be included in the representation, the second step of approximation will follow.
The similarity is highest at the minimum of A and lowest at the maximum and vice versa the dissimilarity is highest at the maximum and lowest at the minimum.
Moreover there is a complementary variation of similarity and dissimilarity. With increasing dissimilarity between persons, the similarity is decreasing and vice versa.
Thus, the model of complementarities leads to the conclusion to use additionally to A the complements of these distances (Acomplement) as independent variable of the second power function:
Second power function:
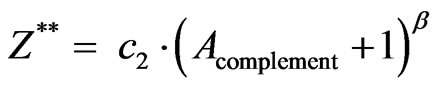 (6)
(6)
A is a variable with the two opposite poles Amin and Amax. The sum of Amin and Amax is a constant. Thus,
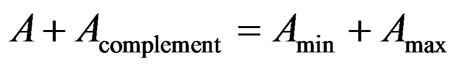 (7)
(7)
 (8)
(8)
That means, the variable Acomplement is increasing according to the same amount as the variable A is decreasing and vice versa (cf. Table 3).
First yin/yang pair:
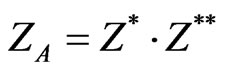 (9)
(9)
 (10)
(10)
with A = |X − Y|.
The first Yin/Yang Pair is related to the secondary diagonal and its parallels.

Figure 7. Power functions of similarity on the one hand or dissimilarity on the other. On the left, the parameter α is negative: “Birds of a feather flock together” and decrease of interpersonal relations with increasing dissimilarity. On the right, the parameter α is positive: “Opposites attract” and increase of interpersonal relations with increasing dissimilarity. This figure is a copy of a figure in [12].
The relationships of the two parameters α and β to each other determine the expressions of the complementarities (similarities, dissimilarities) in each of the shape.
Figure 8 shows in the middle eight several patterns created on the basis of varying α and β.
In every box of the figure the difference |X − Y| is always the abscissa and ZA the ordinate axis. In the middle of the abscissa is X − Y = 0. The relationships of the two parameters to each other determine the expressions of Yin and Yang in each of the patterns.
Figure 8 shows only eight patterns as typical examples. However, according to Chinese philosophy, Yin and Yang are the opposite poles of a single whole. There is not an isolated exclusive Yin, or only a Yang. All transitions occur with a direct and uninterrupted sequence. The natural order is secured by the dynamic equilibrium between Yin and Yang. That means, theoretically an infinite number of patterns should have been produced in Figure 8 for presentation of all of the possible patterns.
For explanation, we intend to characterise 4 types of similar patterns only:
• The Yang pattern (upper pattern);
• The Yin pattern (pattern below);
• The Yin-in-Yang pattern (left pattern) and;
• The Yang-in-Yin pattern (right pattern).
While in the upper pattern Yang is more likely to be in the foreground (Birds of the feather flock together), the pattern below reveals that Yin is more likely to be accentuated (Opposites attract).
Starting from the left side of the upper pattern in the direction of the pattern below from pattern to pattern Yang has retracted itself in favour of Yin. Vice versa,
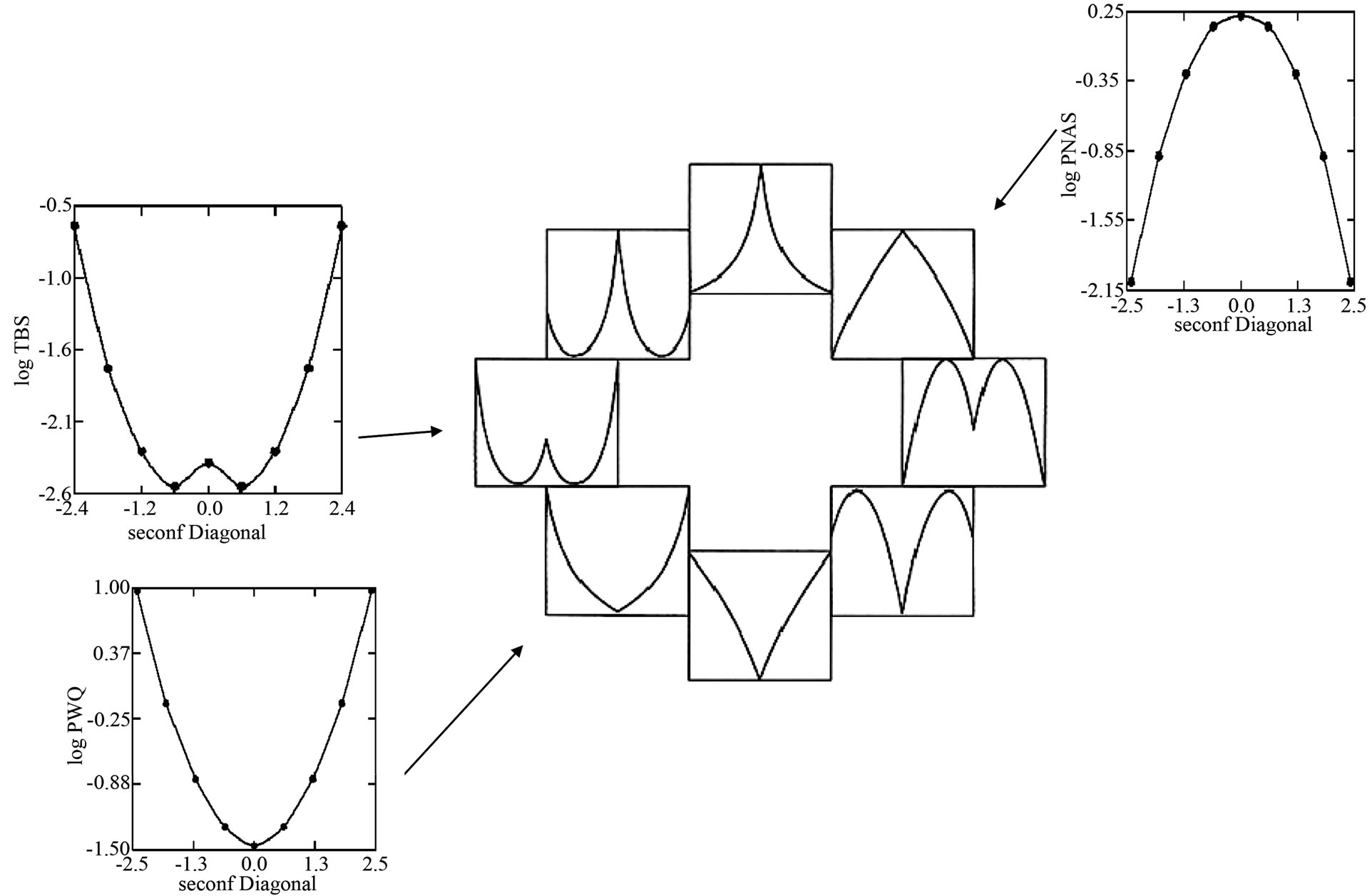
Figure 8. Presentation how two polar forces are interacting as complementary tendencies dynamically with each other on one dimension. Figure 8 is a copy of a figure in [12] according to the function ZA, cf. Equation (10).

Table 3. Example: Amin = 0, Amax = 3.
starting from the right side of the pattern below in the direction of the upper pattern from pattern to pattern Yin has retracted itself in favour of Yang.
The patterns in Figure 8 are arranged that the opposite placed patterns show the opposite meaning regarding Yin and Yang. (For example: “Yang pattern”/“Yin pattern” or “Yin-in-Yang pattern”/”Yang-in-Yin pattern”, etc.).
Note: log-log presentations of patterns in Figure 6 can have similar shapes like the here in Figure 8 shown 8 original patterns. The here on the right side above attached third pattern from the second row in Figure 6 shows Yang is more likely to be in the foreground (Birds of the feather flock together). The here on the left side below attached fourth pattern from the second row in Figure 6 shows Yin is more likely to be in the foreground (Opposites attract). Another pattern is shown from the empirical results (upper pattern on the left side in Figure 8): Yin-in-Yang pattern. The 8 patterns in the middle of Figure 8 are arranged that the opposite placed patterns show the opposite meaning regarding Yin and Yang. (For example: “Yang pattern”/“Yin pattern” or “Yin-in-Yang pattern”/”Yang-in-Yin pattern”, etc.).
The 8 patterns in the middle of Figure 8 can be found on the secondary diagonal and its parallels.
2.2.3. Function ZB for the Description of the Second Yin/Yang Pair
For the purpose of completion, the addition
 (11)
(11)
as opposite of subtraction (A = |X − Y|), is supposed as independent variable of the third power function:
Third power function:
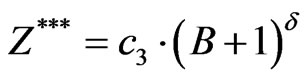 (12)
(12)
and the complement (Bcomplement) is the independent variable of the fourth power function:
Fourth power function:
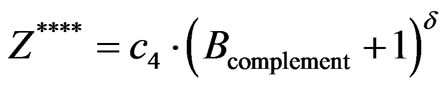 (13)
(13)
In analogy to A and Acomplement:
B + Bcomplement= Bmin + Bmax (14)
Bcomplement = Bmin + Bmax – B (15)
Second yin/yang pair:
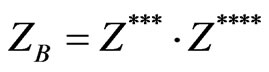 (16)
(16)
 (17)
(17)
including Equation (11).
The second Yin/Yang Pair is related to the main diagonal and its parallels.
This second dimension is placed orthogonal on the first dimension. Thus, these 8 patterns can be found on the main diagonal and its parallels. The upper patterns of Figure 6 (the curvilinear lines regarding the main diagonal: convex and concave are attached on the top of Figure 9 for comparison.
2.2.4. Function ZXY: Intensity Function of Interpersonal Attraction (Social Gestalt)
Because the shapes of the second Yin/Yang pair (Figure 9) can vary independently from the shapes of the first Yin/Yang pair (cf. Figure 8) we assume the intensity of mutual attraction ZXY is proportional to the product of the two functions ZA and ZB:
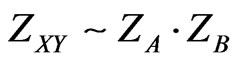 (18)
(18)
Intensity function of interpersonal attraction (Social Gestalt):
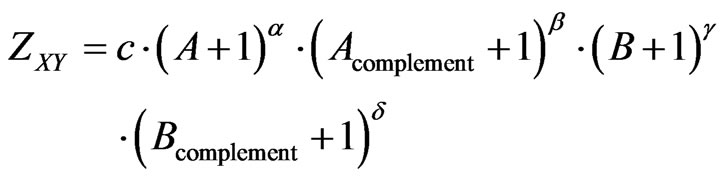 (19)
(19)
with c = constant and the Equations (5), (8), (11) and (15).
The measurement of the variables X, Y and ZXY including the Equations (20) and (21) are depending on the studied object.
Xmin = Ymin (20)
and Xmax = Ymax (21)
We assume with rising ZXY the frequencies of social interactions are proportionally rising. Examples of social interactions are collaboration, friendships, marriages, etc., while examples of characteristics or of qualities of these individual persons (X or Y) are age, labor productivity, education, professional status, etc.
This bivariate Intensity Function is producing threedimensional graphs. Based on the influence of the changes of men and environment the three-dimensional social Gestalts can change the shape resulting in a diversity of social Gestalts. These many Gestalts are classified into Prototypes (cf. Figure 10) in the sense of well-ordered patterns or “Good Gestalts”. Several empirical social Gestalts matching the 5 Prototypes were already taken out and presented in Kretschmer 2002. The distribution of co-author pairs’ frequencies Nij is one of the examples. The non-logarithmic presentation is similar to the left prototype. However, in this paper we are showing
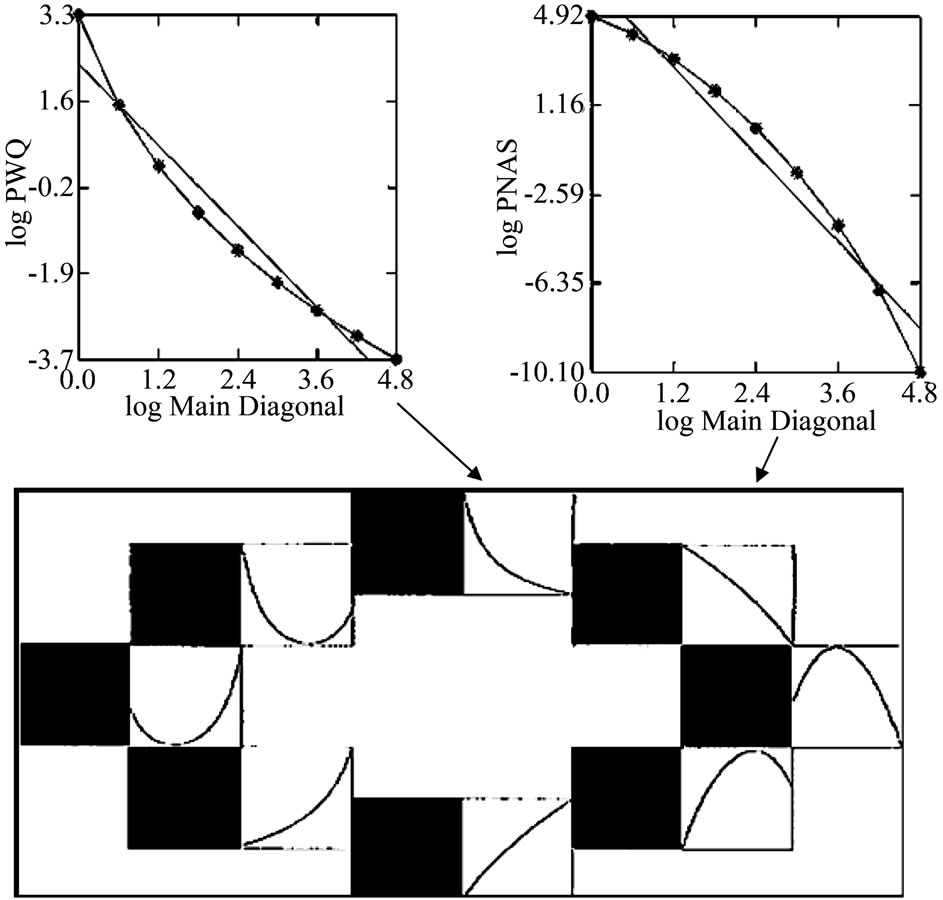
Figure 9. Presentation how two polar forces are interacting as complementary tendencies dynamically with each other on one dimension according to the function ZB, cf. Equation (17).
the corresponding log-log-log presentation only.
2.3. Model for the Intensity Function of the Distribution of Co-Author Pairs’ Frequencies Nij
One of the examples, how to measure the variables X and Y can be shown in relation to the function of the distribution of co-author pairs’ frequencies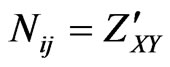 . There is a conjecture by de Solla Price [20], physicist and science historian, that the logarithm of the number of publications is of a higher degree of importance than the number of publications per se.
. There is a conjecture by de Solla Price [20], physicist and science historian, that the logarithm of the number of publications is of a higher degree of importance than the number of publications per se.
Thus, using the logarithm of the number of publications (logi or logj respectively) as personal characteristic “productivity”, we define:
X = logi (22)
Y = log j (23)
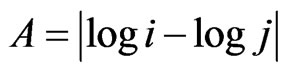 (24)
(24)
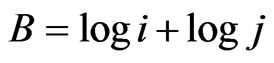 (25)
(25)
Thus:
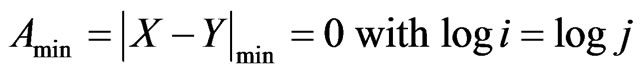 (26)
(26)
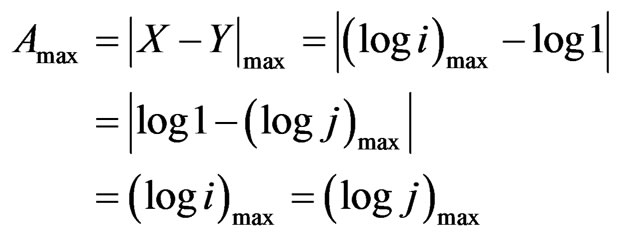 (27)
(27)
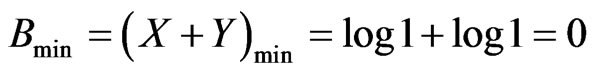 (28)
(28)

Figure 10. Prototypes of social Gestalts (non-logarithmic presentation). Several empirical social Gestalts matching the 5 Prototypes were already taken out and presented in [18].
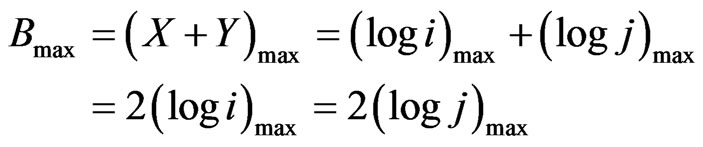 (29)
(29)
Let us lay down a specific value for the maximum possible number of publications i (or j respectively) of an author as standard for such studies, which does not vary depending upon the given sample. It is assumed that the maximum possible number of publications of an author is equal to 1000, i.e.
 (30)
(30)
 (31)
(31)
following:
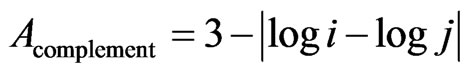 (32)
(32)
 (33)
(33)
The theoretical mathematical function for describing the social Gestalts of the distribution of co-author pairs’ frequencies is resulting in the following logarithmic version:
 (34)
(34)
with c = constant and with the Equations (22) and (23).
Although the field of mutual attraction (or social Gestalt) fails to determine completely individual pairs of persons in terms of the predictability of these individual pairs, the force that emanates from this field generates a statistically balanced evenness among all the individual pairs in their totality (Tendency towards a good social Gestalt). This statistically balanced evenness is enhanced as the number of co-author pairs’ frequencies rises. We refer to Bernoulli’s law of large numbers.
Obtaining large sample sizes is possible in studies of large bibliographies (journals or research areas). The application of logarithmic binning procedure is another method for obtaining this statistically balanced evenness. In conjunction with the model of complementarities, there are different shapes of social Gestalts depending on changing personality and situation or environment.
The function of Nij is a special case of the social Gestalts in social networks described by the general function ZXY.
3. Results
3.1. Introduction
Distributions of co-author pairs’ frequencies of 52 coauthorship networks are studied in total. For 96% of the 52 distributions the squared multiple R is larger than 0.98% and for 77% even equal or larger than 0.99 (cf. Figure 13). The social Gestalts in comparison with empirical data of these 77% will be presented in the Appendix.
On the first step, two of them are selected here for explanation [21]. Figure 11 shows the overlay of the distribution of co-author pairs’ frequencies (logNij) and the corresponding Gestalt regarding the co-authorship network obtained from the journal PNAS (1980-1998). As predicted, the empirical values are very well placed on the points, two of theoretical lines touch each other. Therefore, in this connection the squared multiple R = 0.998 is high. Whereas the Gestalt in Figure 11 has a convex shape the Gestalt in Figure 12 is concave.
3.2. Overview about the Studied Networks
• 3.2.1. Distribution of the 52 Networks over Scientific Disciplines
• 29 networks belong to medicine and life sciences;
• 13 to physics, chemistry or technology;
• 7 to humanities and social sciences and;
• 3 of them are general oriented (PNAS, SCIENCE and NATURE).
• 3.2.2. Distribution of the 52 Networks over Resources
• 45 are co-authorship networks obtained from journals (38 of them are taken from the SCI);
• 5 co-authorship networks are the results of field studies;
• 2 are the results of studies of institutes.
3.2.3. Another Overview about the 52 Networks
The total number of co-author pairs’ frequencies Nij per
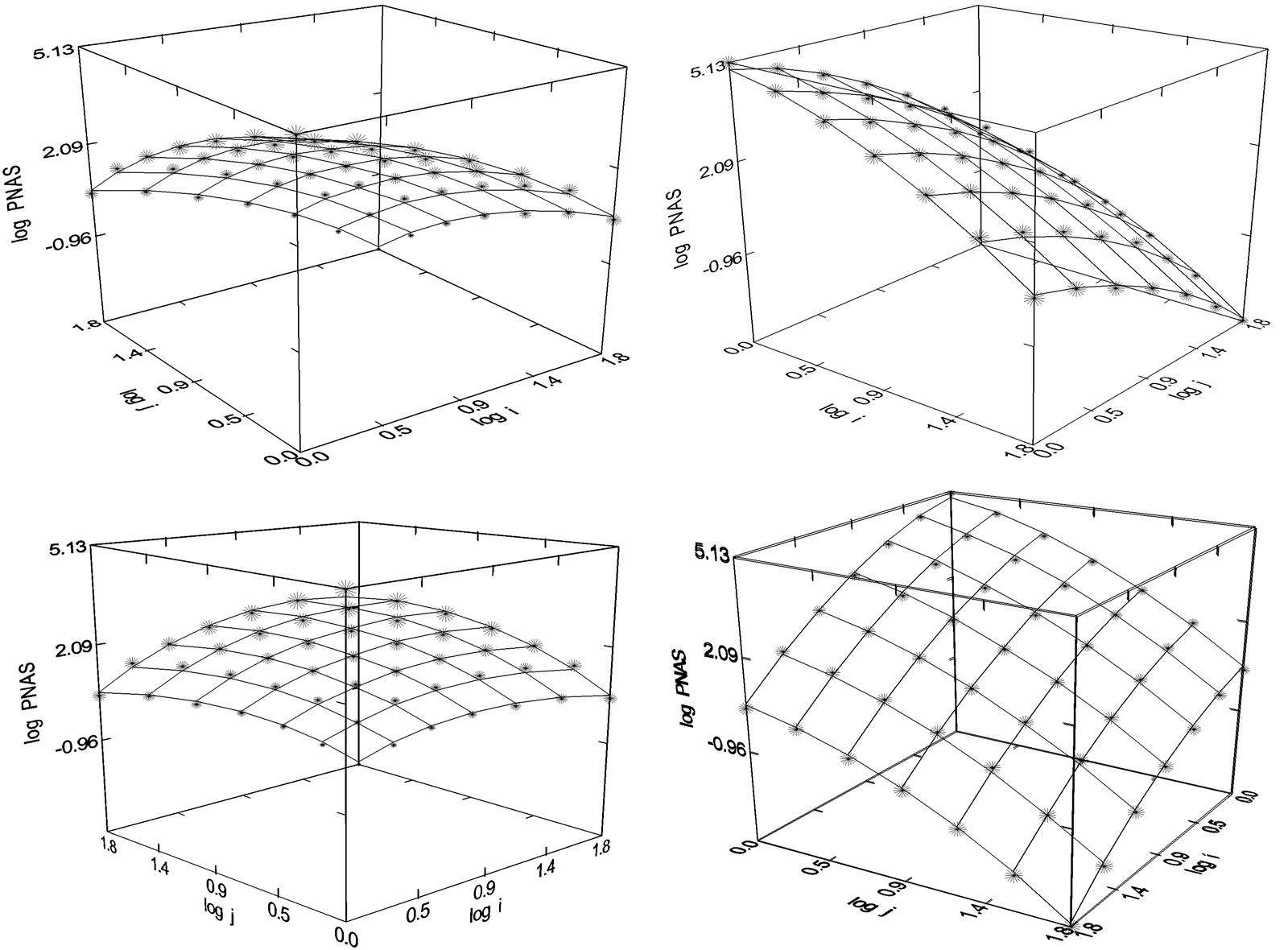
Figure 11. Distribution of co-author pairs’ frequencies (logNij) in dependence on the productivities of the co-authors (logi and logj). The left pattern on the first row is turned around three times. Regression analysis: Dep. Var: PNAS (1980-1998), N = 48, R2 = 0.998, P = 0.000, F-Ratio = 5526.476, NT = 634,014, Authors: 80,058, Articles: 32,486, logimax = 1.806 (Presented in [20]).

Figure 12. Distribution of co-author pairs’ frequencies (logNij) in dependence on the productivities of the co-authors (logi and logj). The left pattern on the first row is turned around three times. Regression analysis: Dep. Var: Psychology of Women Quarterly (1976-2009); N = 16, R2 = 0.998, P = 0.000, F-ratio = 1354.52, NT = 4342, Authors: 2569, Articles: 1146, logimax = 0.903 (Presented in [20]).

Figure 13. Frequency of co-authorship networks (ordinate) in dependence on the squared multiple R (abscissa) after regression analysis (empirical distribution of co-author pairs’ frequencies (logNij) and social Gestalt). Note: The squared multiple R is ranging between 0.944 and 1.000 and the median is equal to 0.993. For 96% of the co-authorship networks the squared multiple R is larger than 0.98.
network is ranging from 612 to 1,972,684 and the median is equal to 105,720.
• The number of papers is ranging between 162 and 91,442. The median is equal to 5936.
• The number of authors is ranging between 91 and 111,447. The median is equal to 13,609.
• The average number of authors per article is ranging between 1.2 and 6.49 with the median equal to 3.745.
• The total number of co-author pairs’ frequencies Nij is ranging from 612 to 1,972,684 and the median is equal to 105,720.
• After logarithmic binning the number of empirical data as basis for the regression analysis is ranging between 6 and 79 with the median equal to 35.5. This number of empirical data is depending on (logi)max.
• The distribution of the frequencies of co-authorship networks in dependence on (logi)max and the frequencies of them with Gestalts, different from the convex shape are shown in Figure 14.
• The F-ratio (ratio of the mean square of the regression and the mean square of the residual) is ranging between 118 and 9024 with the median equal to 1385. Beside the squared multiple R the F-Ratio is also a measure of the goodness-of-fit. The connection to the total number of Nij, to the relative number of authors per article, and to the number of empirical data in the matrix of the bins (cells) is shown in Figure 15.
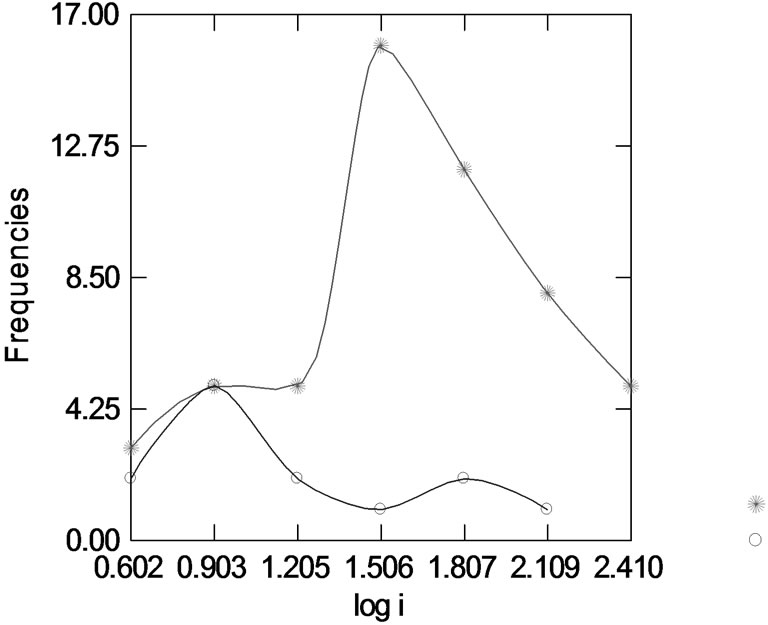
Figure 14. Distribution of frequencies of co-authorship networks in dependence on (logi)max (upper line) and frequencies of them with Gestalts, different from the convex shape (lower line). The last are 13 in total. Note: Shapes, different from convex Gestalts can be mainly found in co-authorship networks with lower (logi)max. Whereas the frequency of co-authorship networks with convex Gestalts is increasing with increasing (logi)max the frequency of coauthorship networks with different Gestalts is decreasing.
4. Discussion and Conclusion
A mathematical model is presented for describing bivariate distributions of co-author pairs’ frequencies in dependence on the productivities of the collaborators. This model is based on a special fundamental principle of social group formations in connection with complementarities.
Holistic entities with balancing interactions of forces are considered both by Gestalt psychology and Yin/Yang teaching.
• The “tendency towards a good Gestalt” is a special feature of the Gestalt psychology;
• The complementarities are a special feature of the Yin/Yang theory.
In conclusion, the social Gestalt is a model that comprised the “tendency towards a good Gestalt” but the definite rules are obtained by considering the complementarities.
As a special method the logarithmic binning procedure is applied. Because of theoretical expectations regarding the complementarities, Gestalts with various shapes are resulting. The correlations between empirical and theoretical values are very high in 52 studied co-authorship networks (For 96% of these networks the squared multiple R is larger than 0.98).
First Proposal for studies in future:
Discoveries of laws (or STRONG regularities respectively) belong to the main goals in basic research. Further, the correlations between empirical and theoretical values are very high in 52 studied co-authorship networks (For 96% of these networks the squared multiple R is larger than 0.98. This quality is comparable with Lotka’s law, Bradford’s law or Zipf’s law).
Therefore, the main question is arising: Is there a new informetric law (or STRONG regularity respectively) existing?
In this line a hypothesis can be formulated regarding a possible general validity in co-authorship networks:
A fundamental principle of social group formations is general existing regarding the preference in collaboration between individual authors. This social group formation can be described by a mathematical model.
For verification of this hypothesis, extensive and systematic studies have to be carried out for several specifications, for example several scientific fields, several journals, special kinds of limitations or advantages, etc. As mentioned above crucial determinants of the mathematical model are both the ‘tendency towards a good Gestalt’ and complementary tendencies interacting dynamically with each other, so that the entire system is

Figure 15. The F-ratios of the regression analyses are increasing with the total number of Nij (left pattern), with the relative number of authors per article (middle) and with the number of cells in the square matrix (compare Table 2) of co-author pairs (logNij) (right pattern).
open to change (changing shapes).
Further, in practice we already could find concave patterns more frequently in small bibliographies with low maximum productivity of authors (maximum 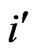 or
or 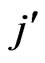 per author is between 7 and 30). This kind of pattern could also be found in gender oriented journals. There are also differences in the behavior between male and female authors. We assume maybe there is a relation to minorities (concave). But we should investigate this question further and more in detail in future.
per author is between 7 and 30). This kind of pattern could also be found in gender oriented journals. There are also differences in the behavior between male and female authors. We assume maybe there is a relation to minorities (concave). But we should investigate this question further and more in detail in future.
Vice versa, large bibliographies including high productivity authors (maximum i or j higher than 100) and natural sciences or medicine show the tendencies to convex patterns.
There are many bibliographies between the clear concave or clear convex patterns like the Yin/Yang teaching is speaking: There is not only Yin or only Yang.
Some of the possible questions for future studies:
• Is there a change of the shape of the well-ordered distributions of co-author pairs’ frequencies over time as suggested in Figure 3?
• Are there special conditions the shapes of the social Gestalt apt to special poles as we can expect by the empirical results mentioned above?
Self-similarity and power laws are successful in describing complex networks of interactions. Scale-free network models describe many natural and social phenomena, for example networks of interacting components of a living cell or social networks.
Further, there is already a successful example as a result from former studies available (cf. Figure 16). Thus, the following question for further studies is arising: Are self-similarities of Gestalts in co-author pair’s networks in general existing?
5. Acknowledgements
The authors thank Johannes Stegmann for his helpful comments. The authors wish also to thank Holger Heitsch
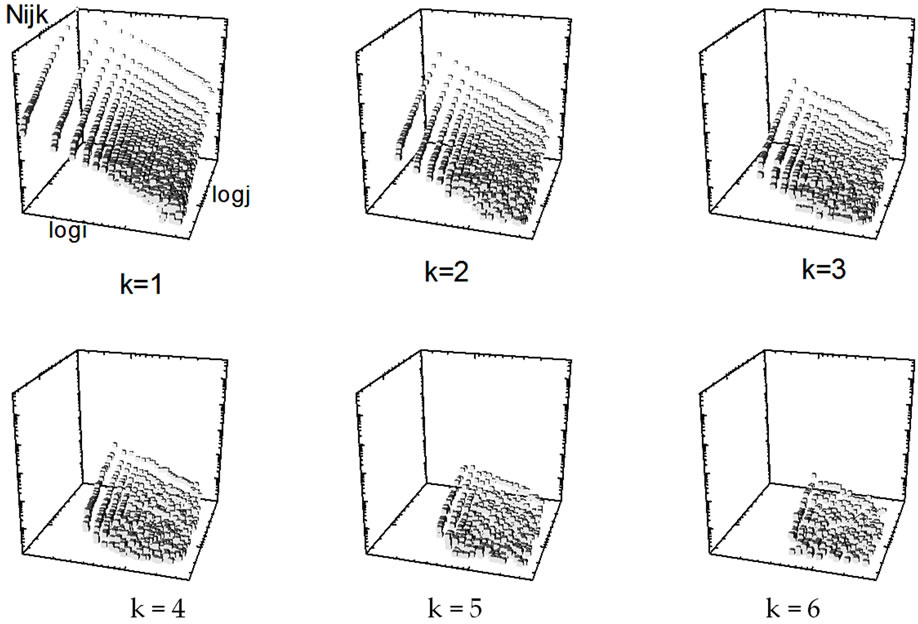
Figure 16. Self-similarity in the co-author pair’s network of a journal (NATURE, 1980-1989).
and Jan Johannes for programming. Moreover, the authors thank WISELAB at the Dalian University of Technology, Dalian, China, and especially Professor Liu Zeyuan, for invitation as Keynote Speakers for presentation the first ideas of the present paper at the 5th International Conference on Webometrics, Informetrics and Scientometrics and 10th COLLNET Meeting, 13-16 September 2009, Dalian, China [25].
REFERENCES
- W. Glänzel, “Coauthorship Patterns and Trends in the Sciences (1980-1998): A Bibliometric Study with Implications for Database Indexing and Search Strategies,” Library Trends, Vol. 50, No. 3, 2002, pp. 461-473.
- C. L. Borgman and J. Furner, ”Scholarly Communication and Bibliometrics,” In: B. Cronin, Ed., Annual Review of Information Science and Technology, Vol. 36, Information Today, Medford, 2002, pp. 3-72. doi:10.1002/aris.1440360102
- W. Glänzel and A. Schubert, “Analyzing Scientific Networks through Co-Authorship,” In: H. F. Moed, W. Glänzel and U. Schmoch, Eds., Handbook of Quantitative Science and Technology Research, Kluwer Academic Publisher, Dordrecht, 2006, pp. 257-276.
- L. M. Liang and L. Zhu, “Major Factors Affecting China’s Inter-Regional Research Collaboration: Regional Scientific Productivity and Geographical Proximity,” Scientometrics, Vol. 55, No. 2, 2002, pp. 287-316. doi:10.1023/A:1019623925759
- P. S. Nagpaul, “Exploring a Pseudo-Regression Model of Transnational Cooperation in Science,” Scientometrics, Vol. 56, No. 3, 2003, pp. 403-416. doi:10.1023/A:1022335021834
- F. Havemann, M. Heinz and H. Kretschmer, “Collaboration and Distances between German Immunological Institutes—A Trend Analysis, “Journal of Biomedical Discovery and Collaboration, Vol. 1, 2006, p. 6. doi:10.1186/1747-5333-1-6
- J. S. Katz, “Geographical Proximity and Scientific Collaboration,” Scientometrics, Vol. 31, No. 1, 1994, pp. 31- 43. doi:10.1007/BF02018100
- T. Braun, A. Schubert and W. Glänzel, “Publication and Cooperation Patterns of the Authors of Neuroscience Journals,” Scientometrics, Vol. 51, No. 3, 2001, pp. 499- 510. doi:10.1023/A:1019643002560
- L. Egghe, “A Model for the Size-Frequency Function of Co-Author Pairs,” Journal of the American Society for Information Science and Technology, Vol. 59, No. 13, 2008, pp. 2133-2137. doi:10.1002/asi.20900
- A. J. Lotka, “The Frequency Distribution of Scientific Production,” Journal of the Washington Academy of Science, Vol. 16, No. 12, 1926, pp. 317-323.
- S. A. Morris and M. L. Goldstein, “Manifestation of Research Teams in Journal Literature: A Growth Model of Papers, Authors, Collaboration, Co-Authorship, Weak Ties, and Lotka’s Law,” Journal of the American Society for Information Science and Technology, Vol. 58, No. 12, 2007, pp. 1764-1782. doi:10.1002/asi.20661
- H. Kretschmer and T. Kretschmer, “Lotka’s Distribution and Distribution of Co-Author Pairs’ Frequencies,” Journal of Informetrics, Vol. 1, No. 4, 2007, pp. 308-337. doi:10.1016/j.joi.2007.07.003
- H. Kretschmer and T. Kretschmer, “Varying Shapes of Co-Author Pairs’ Distributions,” Collnet Journal of Scientometrics and Information Management, Vol. 2, No. 1, 2008, pp. 45-61.
- R. Kundra, D. de B. Beaver, H. Kretschmer and T. Kretschmer, “Co-Author Pairs’ Frequencies Distribution in Journals of Gender Studies,” Collnet Journal of Scientometrics and Information Management, Vol. 2, No 1, 2008, pp. 63-71.
- H. Guo, H. Kretschmer and Z. Liu, “Distribution of Co-Author Pairs’ Frequencies of the Journal of Information Technology,” Collnet Journal of Scientometrics and Information Management, Vol. 2, No. 1, 2008, pp. 73-81 doi:10.1080/09737766.2008.10700842
- M. E. J. Newman, “Power Laws, Pareto Distributions and Zipf’s Law,” Contemporary Physics, Vol. 46, No. 5, 2005, pp. 323-351. doi:10.1080/00107510500052444
- H. Kretschmer, “A New Model of Scientific Collaboration. Part I: Types of Two-Dimensional and Three-Dimensional Collaboration Patterns,” Scientometrics, Vol. 46, No. 3, 1999, pp. 501-518. doi:10.1007/BF02459607
- H. Kretschmer, “Similarities and Dissimilarities in Co-Authorship Networks; Gestalt Theory as Explanation for Well-Ordered Collaboration Structures and Production of Scientific Literature,” Library Trends, Vol. 50 No. 3, 2002, pp. 474-497.
- M. Wertheimer, “Über Gestalttheorie,” Erlangen, 1925. Gestalt Theory. In the translation by Willis D. Ellis published in his “Source Book of Gestalt Psychology”, Harcourt, Brace and Co., New York, 1938. Reprinted by the Gestalt Journal Press, New York, 1997.
- D. de S. Price, “Little Science, Big Science,” Columbia University Press, New York, 1963.
- H. Kretschmer, R. Kundra, D. B. de Beaver and T. Kretschmer, “Gender Bias in Journals of Gender Studies,” Scientometrics, Vol. 93, No. 1, 2012, pp. 135-150. doi:10.1007/s11192-012-0661-5
- L. A. Adamic, “Zipf, Power-Laws, and Pareto—A Ranking Tutorial”. http://www.hpl.hp.com/research/idl/papers/ranking/ranking.html
- N. K. Wadhwa, H. Kretschmer and T. Kretschmer, “CoAuthor Pairs’ Frequencies of the National Physical Laboratory India,” Collnet Journal of Scientometrics and Information Management, Vol. 4, No. 2, 2010, pp. 49-55. doi:10.1080/09737766.2010.10700892
- J. Pang, H. Kretschmer and Z. Y. Liu, “Distribution of Co-Author Pairs’ Frequencies in Energy Science and Technology,” Collnet Journal of Scientometrics and Information Management, Vol. 3, No. 2, 2009, pp. 11-18. doi:10.1080/09737766.2009.10700872
- H. Kretschmer and T. Kretschmer, “Who Is Collaborating with Whom? Explanation of a Fundamental Principle,” In: H. Y. Hou, B. Wang, S. B. Liu, Z. G. Hu, X. Zhang and M. Z. Li, Eds., Proceedings of the 5th International Conference on Webometrics, Informetrics and Scientometrics and 10th Collnet Meeting, Dalian, 13-16 September 2009, unpublished.
1. Appendix
First the methods are described in detail for counting the co-author pairs and the logarithmic binning procedure. The visualization of the three-dimensional graphs of the social Gestalts is explained.
Second the 40 Gestalts with overlaid empirical data, under the condition the corresponding squared multiple R is equal or larger than 0.99, will be presented.
1.1. Method for Counting Ni’j’
Given is an artificial bibliography including 8 papers (names of authors: A, B, ···).
1) A; 4) D, A, F 7) H, G
2) B 5) C 8) H, G, A
3) D, E 6) G, H
The number of publications  (or
(or 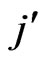 respectively) per author P (or Q respectively) is determined by resorting to the normal count procedure’. Each time the name of an author appears, it is counted (e.g. A three times: once in the first paper, and once each in the 4th and 8th papers).
respectively) per author P (or Q respectively) is determined by resorting to the normal count procedure’. Each time the name of an author appears, it is counted (e.g. A three times: once in the first paper, and once each in the 4th and 8th papers).
Pairs P, Q are marked in the cells of the matrix under the condition of both the first authors P count 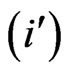 and the second authors Q count
and the second authors Q count , i.e. the authors are ordered according to
, i.e. the authors are ordered according to  or
or 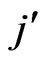 respectively in both the row and the column.
respectively in both the row and the column.
Under the condition, the place of the authors in the by-line is not taken into consideration the symmetrical matrix is resulting. For example, the pair G,A is marked two times: once under the condition G count 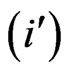 and A count
and A count 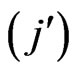 and once under the condition A count
and once under the condition A count 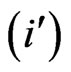 and G count
and G count  (cf. Table 4).
(cf. Table 4).
In the symmetrical matrix, one can determine for each author P the number of his collaborators NP. NP is equal to the Degree Centrality in Social Network Analysis (SNA).
The matrix of 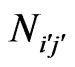 (derived from the symmetrical matrix, cf. Table 5) is the representation of the number of pairs
(derived from the symmetrical matrix, cf. Table 5) is the representation of the number of pairs  with authors who have
with authors who have 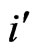 publications per author, with authors who have
publications per author, with authors who have  publications per author included in the bibliography. For example, the pairs E,D and F,D from Table 4 are counted as N1'2' = 2 and N2'1' = 2 in the matrix of
publications per author included in the bibliography. For example, the pairs E,D and F,D from Table 4 are counted as N1'2' = 2 and N2'1' = 2 in the matrix of 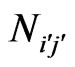 (Table 5).
(Table 5).
1.2. Logarithmic Binning
In general, an important problem when dealing with experimental data is to reduce the amount of stochastic noise. For example, to get a good fit of a straight line (log-log scale plot of power functions, for example Lotka’s distribution) the logarithmic binning procedure can be used [16]. As already mentioned in paragraph 2.1., to get a proper fit, we need to bin the data  into exponential wider bins. Each bin is a fixed multiple wider than the one before it. For example, choosing the multiplier of 2 we receive the intervals 1 to 2, 2 to 4, 4 to 8, 8 to 16, etc.··· i.e. the sizes or widths of the bins (∆i) are 1, 2, 4, 8, etc.··· The number of samples in a bin should be divided by the width of this bin to get a count per unit interval of i. In other words, the new value in a bin is simply the arithmetic average of all the points in the bin (Example, cf. Tables 6 and 7).
into exponential wider bins. Each bin is a fixed multiple wider than the one before it. For example, choosing the multiplier of 2 we receive the intervals 1 to 2, 2 to 4, 4 to 8, 8 to 16, etc.··· i.e. the sizes or widths of the bins (∆i) are 1, 2, 4, 8, etc.··· The number of samples in a bin should be divided by the width of this bin to get a count per unit interval of i. In other words, the new value in a bin is simply the arithmetic average of all the points in the bin (Example, cf. Tables 6 and 7).
The bins in Table 7 appear to be of constant width on the log-log scale (log1 = 0, log2 = 0.301, log4 = 0.602).
After binning, the “new” distribution shows some
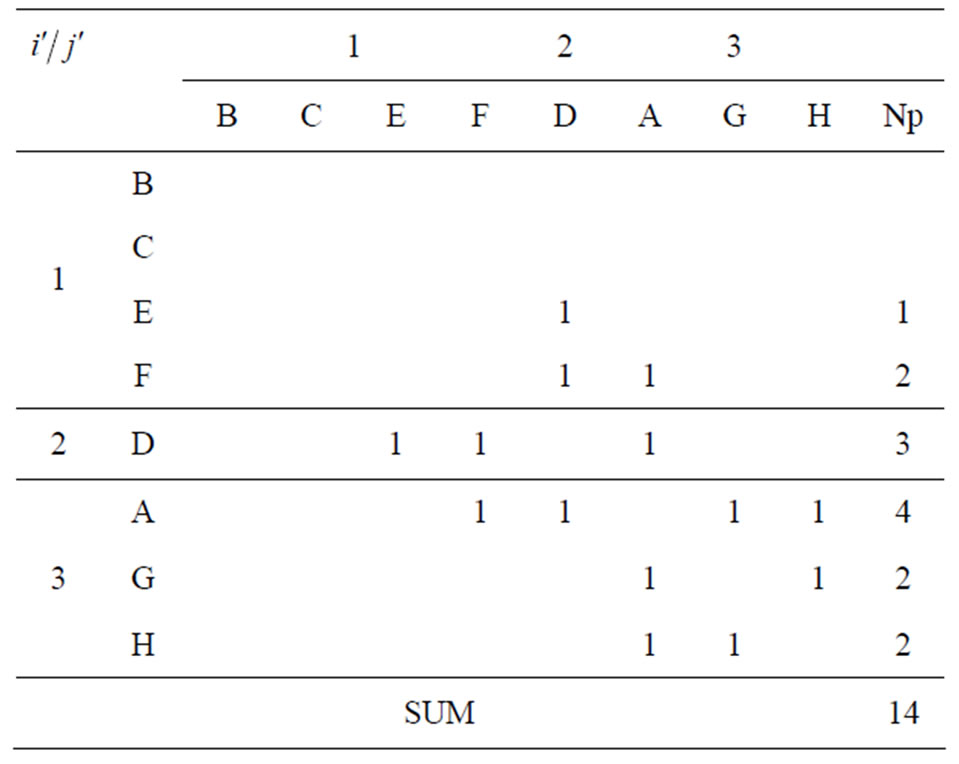
Table 4. Symmetrical matrix.

Table 5. Matrix of co-author pairs Niʹjʹ.

Table 6. Example before logarithmic binning (Y = Number of Authors with iʹ publications per author).

Table 7. Example before logarithmic binning (Y = Number of Authors with iʹ publications per author).
modified parameters related to the distribution without binning. In analogy to Lotka’s distribution, Figure 17 shows the log-log scale plot of the power distribution of users among web sites [21] before logarithmic binning. Figure 18 is the result after logarithmic binning. The exponentially wider bins appear evenly spaced on a log scale (Compare Figure 18 with Figure 17, before binning).
We propose in this paper a new version of logarithmic binning, i.e. the logarithmic binning procedure regarding bivariate distributions hence producing three-dimensional graphs (log-log-log scale plot). The bivariate distribution of co-author pairs’ frequencies ( ) should be considered,
) should be considered,  and
and  will be counted by using the normal count procedure (Counting how many times an author appears in bibliographies).
will be counted by using the normal count procedure (Counting how many times an author appears in bibliographies).  between authors with
between authors with 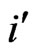 publications per author and authors with
publications per author and authors with 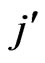 publications per author is a function of
publications per author is a function of  and
and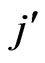 :
:
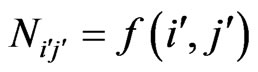 (35)
(35)
In other words:  is the number of co-author pairs. We were using the same method for counting
is the number of co-author pairs. We were using the same method for counting  as described in [12] and in paragraph 6.1.
as described in [12] and in paragraph 6.1.
In case we are starting with the matrix of co-author pairs’ frequencies  before logarithmic binning (Example, cf. Table 8), we need to bin both the data
before logarithmic binning (Example, cf. Table 8), we need to bin both the data  and
and 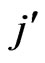 into exponential wider bins.
into exponential wider bins.
The logarithmic binning procedure is applied in our paper choosing the multiplier of 2.
Regarding 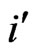 or
or 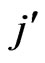 we receive the intervals 1 to 2, 2 to 4, 4 to 8, 8 to 16, etc.··· For each bin we have ordered the corresponding first value of
we receive the intervals 1 to 2, 2 to 4, 4 to 8, 8 to 16, etc.··· For each bin we have ordered the corresponding first value of 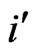 (or
(or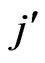 ) to this bin. Thus, the sequence of bins i or j is: i (i=1, 2, 4, 8, 16, 32, 64, 128, 256). The same holds for the bins j. The sizes or widths of the bins (∆i) are: 1, 2, 4, 8, 16 etc.··· The same holds for (∆j).
) to this bin. Thus, the sequence of bins i or j is: i (i=1, 2, 4, 8, 16, 32, 64, 128, 256). The same holds for the bins j. The sizes or widths of the bins (∆i) are: 1, 2, 4, 8, 16 etc.··· The same holds for (∆j).
However, because of bivariate presentation the width of a bin (cellij) in the matrix is the product of ∆i and ∆j equal to (∆i∙∆j), cf. Table 9.
The sum  in a bin (cellij), cf. Table 10, has to be divided by the width of the bin: (∆i∙∆j). In other words, the new value in a bin is simply the arithmetic average of all the points in the bin, cf. Table 11. For example, the value in the bin (cell24) with i = 2 and j = 4 is as follows:
in a bin (cellij), cf. Table 10, has to be divided by the width of the bin: (∆i∙∆j). In other words, the new value in a bin is simply the arithmetic average of all the points in the bin, cf. Table 11. For example, the value in the bin (cell24) with i = 2 and j = 4 is as follows:
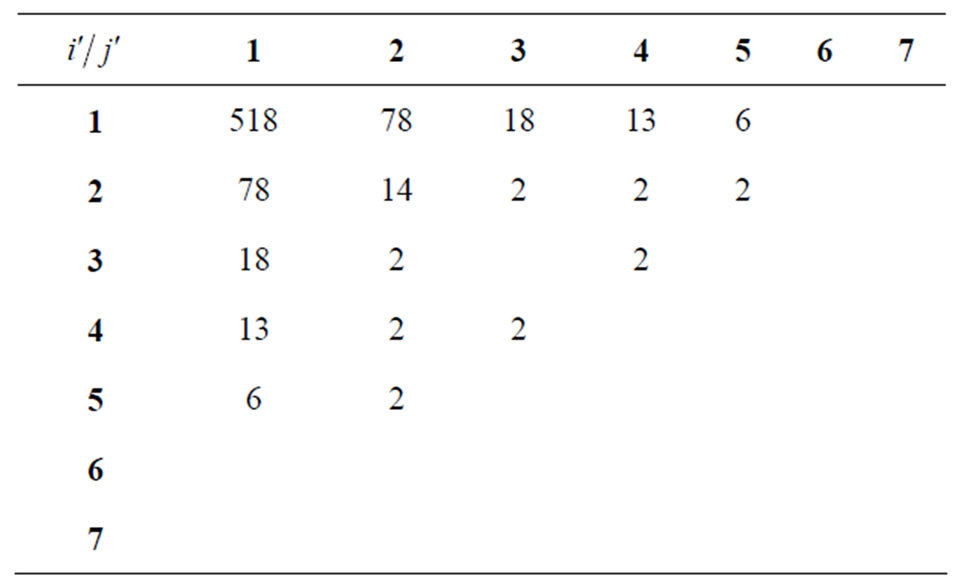
Table 8. Matrix of Niʹjʹ before logarithmic binning.

Figure 17. Log-log scale plot of the distribution of users among web sites (This figure is a copy of [22]).
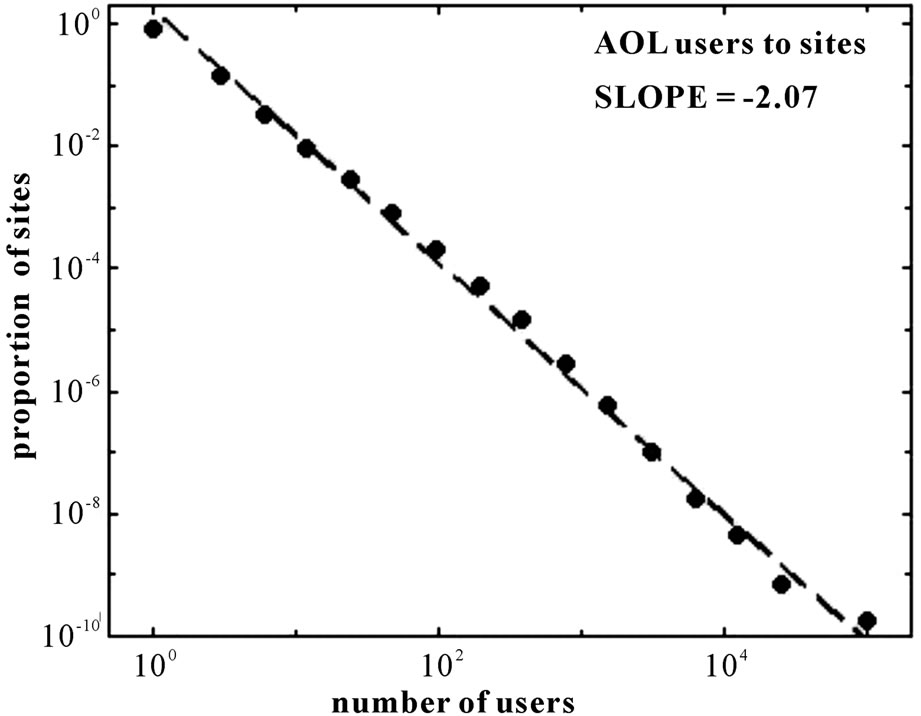
Figure 18. Binned distribution of users (This figure is a copy of [21]).
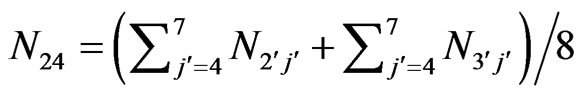 (36)
(36)
There are three advantages of the logarithmic binning procedure in combination with the following log-log-log scale presentation of the matrix above (logi, logj, and logNij):
• Reducing the amount of stochastic noise;
• The exponentially wider bins appear evenly spaced on a log scale;
• On the secondary diagonal the sum of logi and logj is a constant (cf. Equation (1)). The same holds on the corresponding parallels but with different constants each;
• On the main diagonal the absolute difference of logi and logj is a constant (cf. Equation (2)). The same holds on the corresponding parallels but with different constants each.
Using the log-log-log presentation after this procedure, we are starting in this paper with the square matrix of coauthor pairs (logNij), presented at the beginning of this paper in Table 2, as basis for the studies. In Table 2 the sequence of logi (rows) is as follows: logi (logi = 0, 0.301, 0.602, 0.903, 1.204, 1.505, 1.806, 2.107, 2.408), the same is hold for logj (columns). The main diagonal of a square matrix is the diagonal which runs from the top left corner to the bottom right corner (green colored in Table 2). The secondary diagonal is the diagonal of a square matrix running from the lower left entry to the upper right entry (red colored in Table 2).
1.3. Method of Gestalt Visualization
We are using the mathematical model of social Gestalts for describing co-author pairs’ frequencies [12] in form of the log-log-log presentation (Equations (34), with Equations (22) and (23)). For visualization of the theoretical patterns (Social Gestalts) the Function Plot of SYSTAT is used and the Scatterplot for the empirical patterns. After regression analysis the obtained 4 parameters α, β, γ, and δ plus constant are entered into Equation (34).
Scale Range: The maximum and minimum values to appear on the axis are specified. Any data values outside these limits will not appear on the display. The minimum for the X-axis is specified as 0 (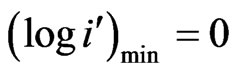 ) and the maximum is equal to the maximum bin
) and the maximum is equal to the maximum bin 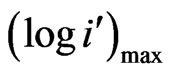 of the empirical data (For example, in Table 11:
of the empirical data (For example, in Table 11:
 = log4). The same holds for the Y-axis
= log4). The same holds for the Y-axis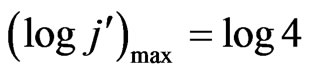 . The minimum and maximum logarithm values for the Z-axis are selected according to
. The minimum and maximum logarithm values for the Z-axis are selected according to
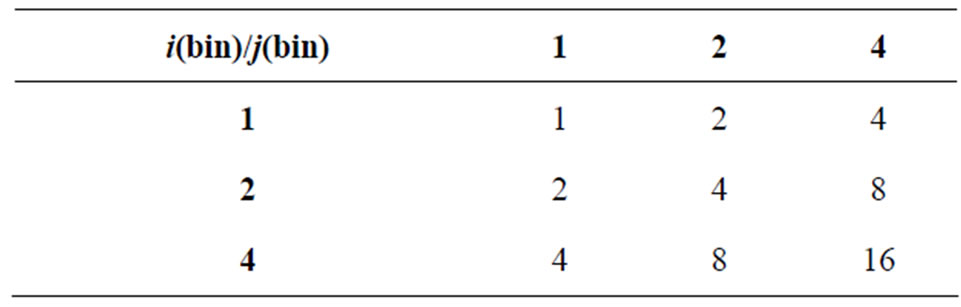
Table 9. Matrix of (∆i) × (∆j) = i(bin) × j(bin).

Table 10. Matrix of Sum Niʹjʹ in a bin (cell).
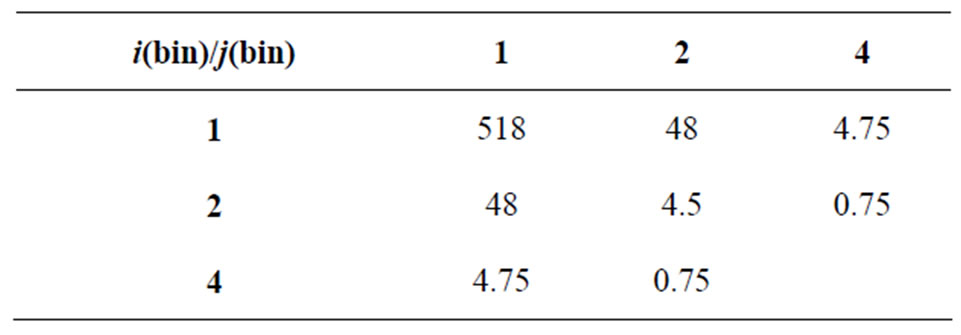
Table 11. After logarithmic binning: Matrix of Niʹjʹ (count) = average = (Sum Niʹjʹ in a bin)/i(bin) × j(bin).
the minimum or maximum logarithm values of the whole Gestalt produced by the function. In case there are empirical values greater or less than these two theoretical values, the minimum or maximum of the Z-axis has to be extended accordingly. The Surface and Line Style dialog box is used to customize the appearance of lines or surfaces. The used XY Cut Lines are in two directions. The number of cuts in the grid has to be specified by the number of bins 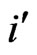 (or
(or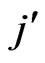 , respectively) minus 1 in the data set. For example, a special data set has 3 bins
, respectively) minus 1 in the data set. For example, a special data set has 3 bins 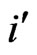 (or
(or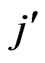 , respectively), as in Table 11; the number of cuts in the grid is specified by 3 − 1 = 2. The resulting number of lines of the theoretical pattern (Gestalt) is equal to the double of the number of bins
, respectively), as in Table 11; the number of cuts in the grid is specified by 3 − 1 = 2. The resulting number of lines of the theoretical pattern (Gestalt) is equal to the double of the number of bins 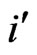 (In the example: 2 × 3 = 6). The number of points where two of the lines intersect, is equal to the square of the number of bins
(In the example: 2 × 3 = 6). The number of points where two of the lines intersect, is equal to the square of the number of bins  (In the example: 32 = 9). This square of the number of bins
(In the example: 32 = 9). This square of the number of bins 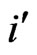 is equal to the number of cells in the corresponding square matrix of co-author pairs (log Nij). The Scale Range of the empirical pattern has to be equal to the theoretical Gestalt or slightly less.
is equal to the number of cells in the corresponding square matrix of co-author pairs (log Nij). The Scale Range of the empirical pattern has to be equal to the theoretical Gestalt or slightly less.
After the overlay of the empirical distribution and the theoretical pattern into a single frame the goodness-of-fit is highest in the case where the empirical values (dots)— obtained from the cells of the matrix—are directly placed on the points where two of the theoretical lines intersect. As the distance between the intersection points and the dots increases, the goodness-of-fit decreases.
The 40 Gestalts with overlaid empirical data are presented in this Appendix below, Figures 19-58. The corresponding squared multiple R is equal or larger than 0.99.
1.4. Gestalts with Overlaid Empirical Data (Dots) and Corresponding Squared Multiple R Equal or Larger than 0.99 (R2 ≥ 0.99)
The presentation of the Gestalts is starting below. The Gestalts are ordered according to the squared multiple R from R2 = 1.000 down to R2 = 0.990. N is equal to the number of dots. NT is equal to the total number of coauthor pairs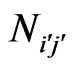 .
.
Independently, on the last page an example is presented regarding the change of the shape of the wellordered distributions of co-author pairs’ frequencies over time. Whereas the first row is showing the pattern based on data from one year of the Journal of Experimental Medicine, the second row shows the pattern based on data from 19 years (cf. Figure 59).

Figure 19. Immunology Today (1980-1998) N = 8, R2 = 1.000; F-ratio: (Residual = 0.000), P = 0.000, NT = 4790, Authors = 1877, Articles = 1040.

Figure 20. Gender & Society (1987-2008), N = 8, R2 = 1.000; F-ratio: (Residual = 0.000), P = 0.000, NT = 778, Authors = 805, Articles = 637.

Figure 21. Women’s and Gender Studies (1995-2007) (Male Authors), N = 6, R2 = 1.000, F-ratio: (Residual = 0.000), P = 0.000, NT = 272, Authors = 901, Articles = 889.
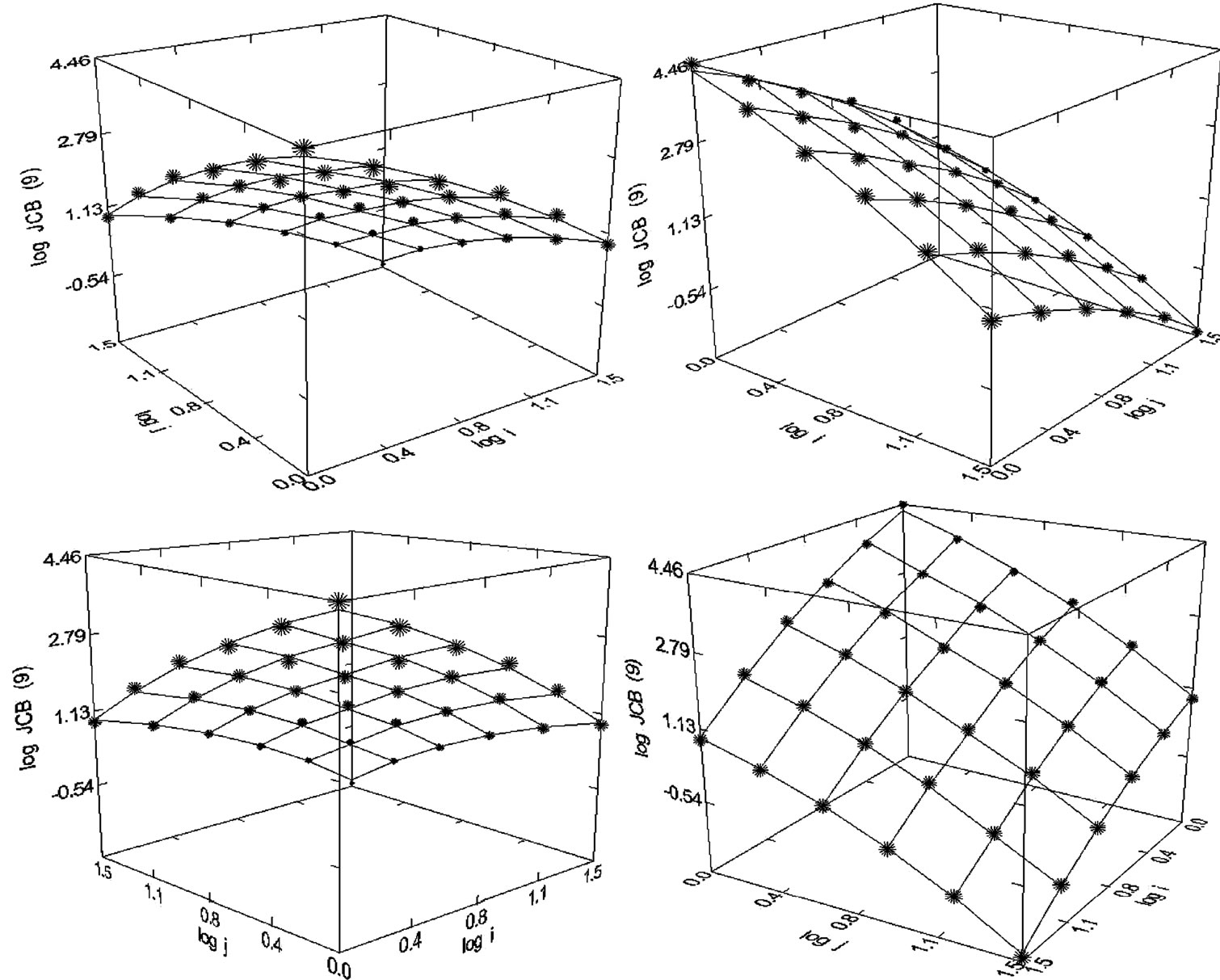
Figure 22. Journal of Cell Biology (1980-1998), N = 36, R2 = 0.999, F-ratio = 5167.788, P = 0.000, NT = 105,720, Authors = 18,125, Articles = 8824.
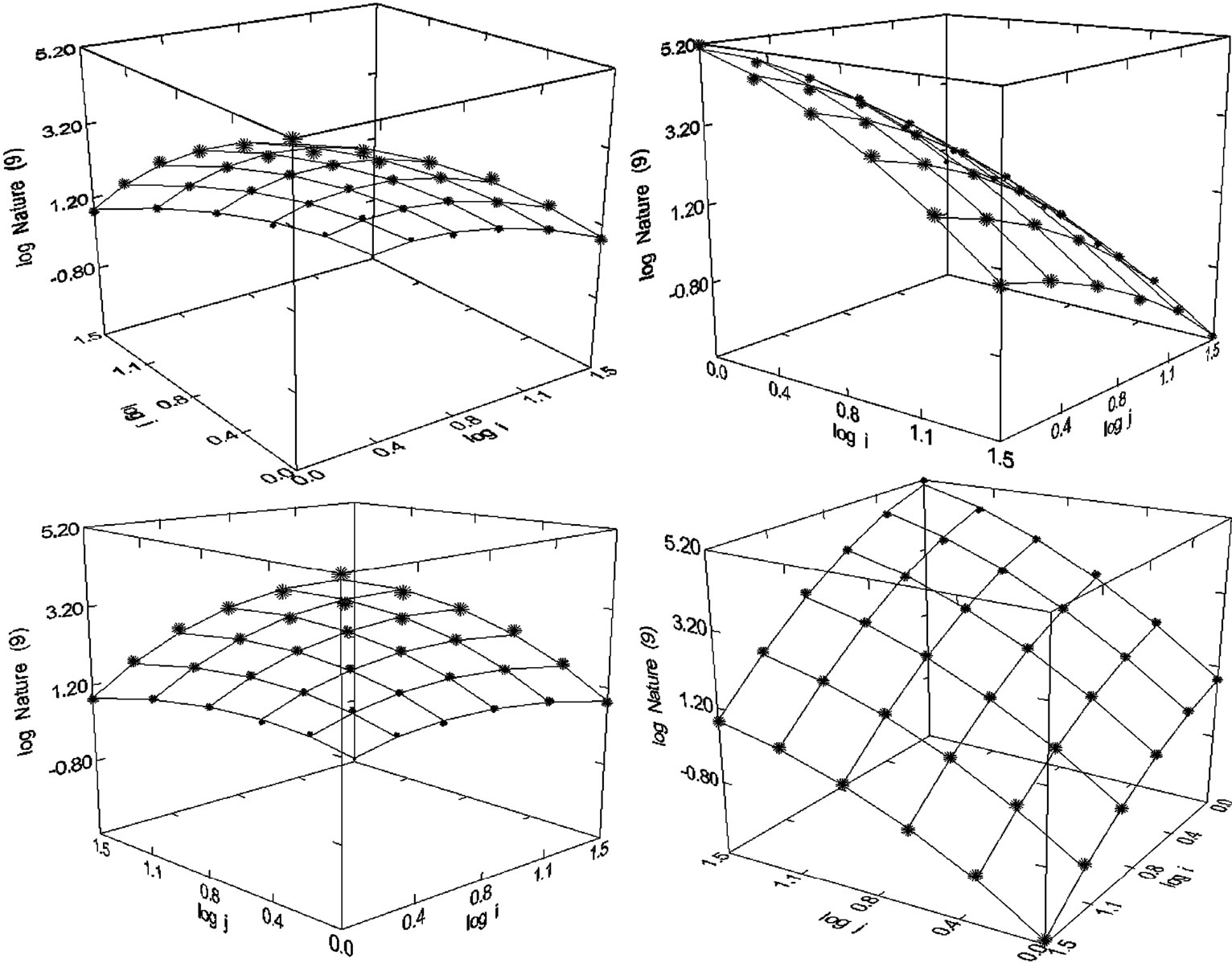
Figure 23. Nature (1980-1998), N = 36, R2 = 0.999, F-ratio = 9,024.2, P = 0.000, NT = 530,778, Authors = 52,937, Articles = 20,673.
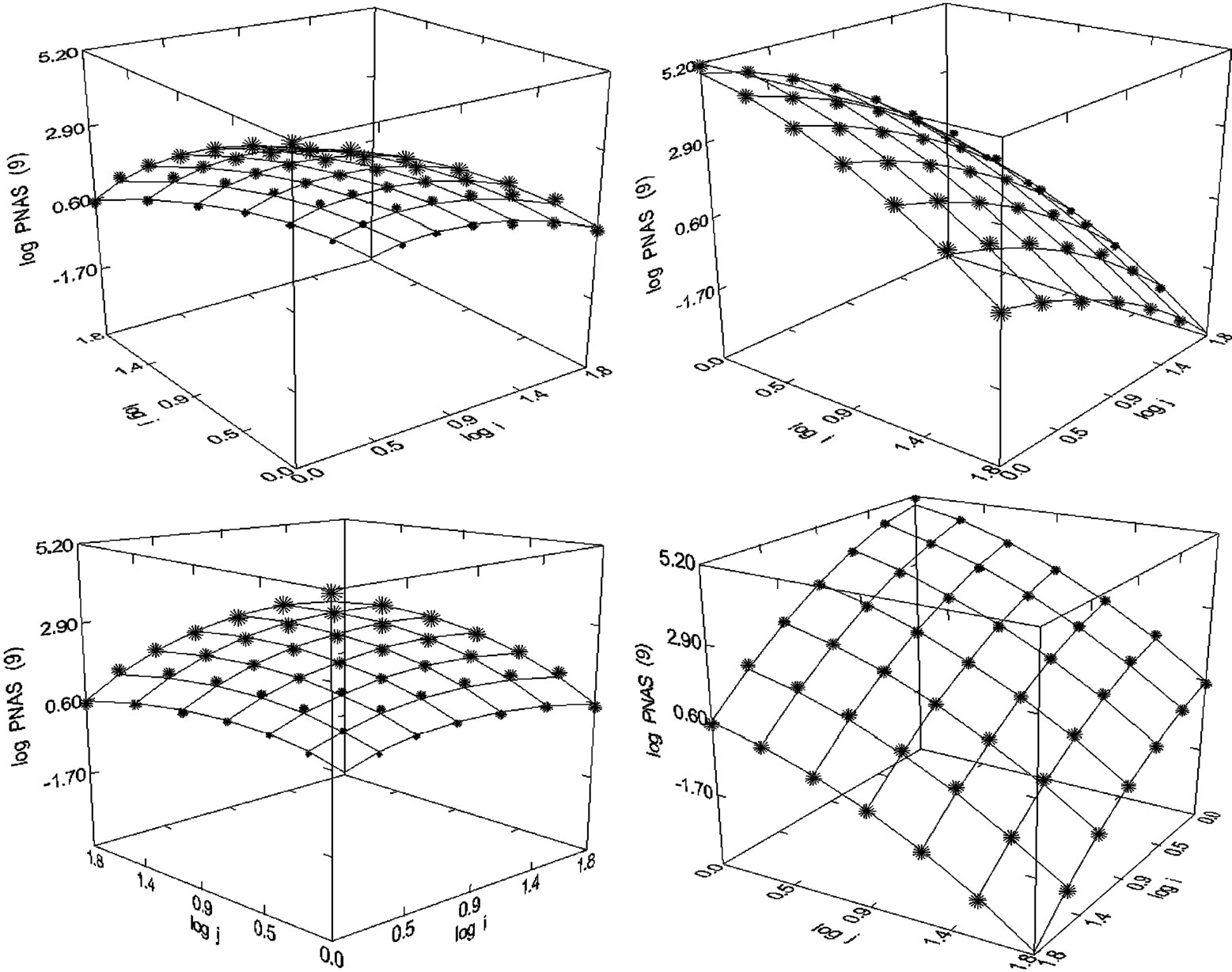
Figure 24. PNAS (1980-1998), N = 48, R2 = 0.998, F-ratio = 5526.476, P = 0.000, NT = 634,014, Authors = 80,058, Articles = 32,486 (Presented in [21]).
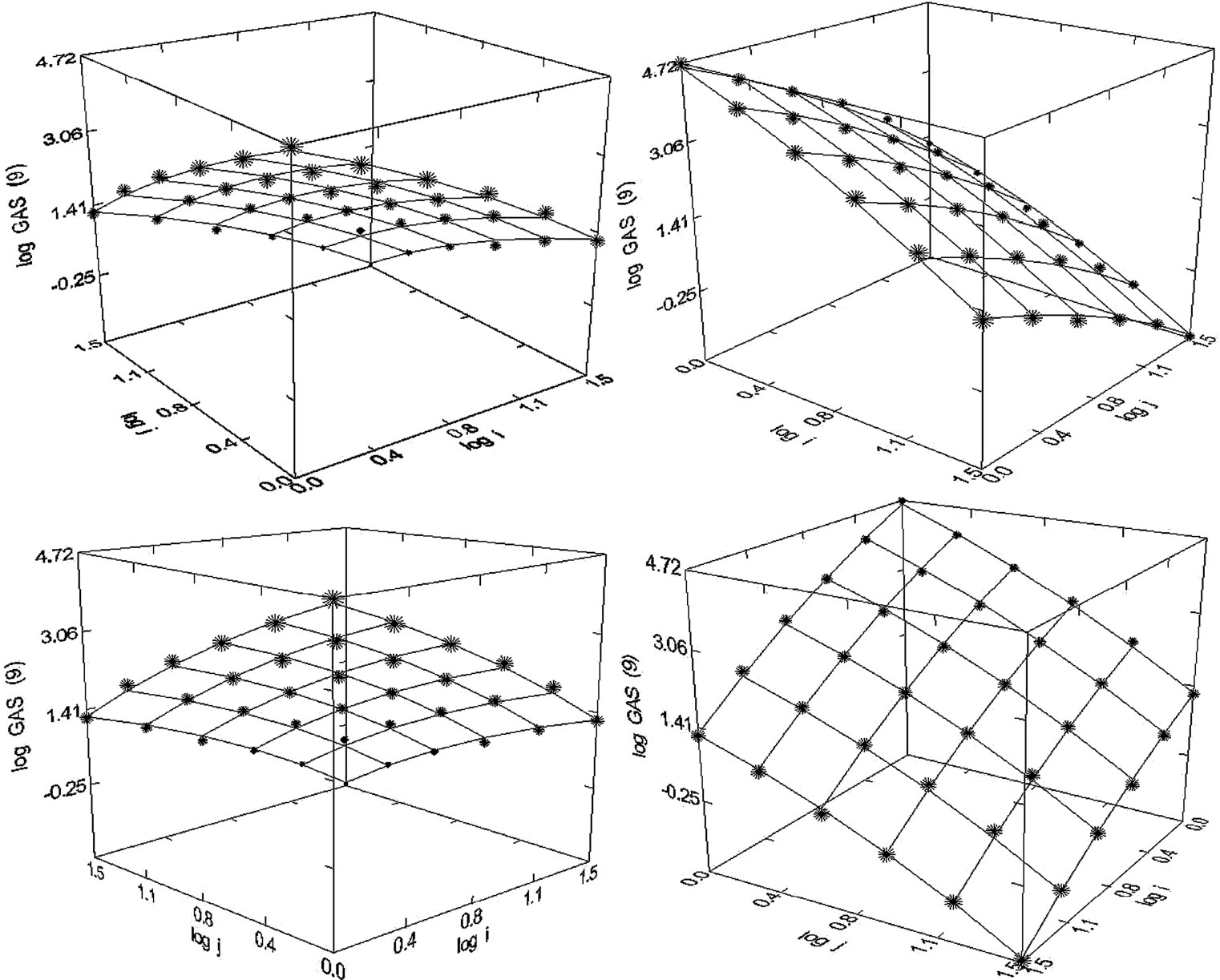
Figure 25. Gastroenterology (1980-1998), N = 36, R2 = 0.998, F-ratio = 4147.541, P = 0.000, NT = 190,608, Authors = 19,750 Articles = 7014.
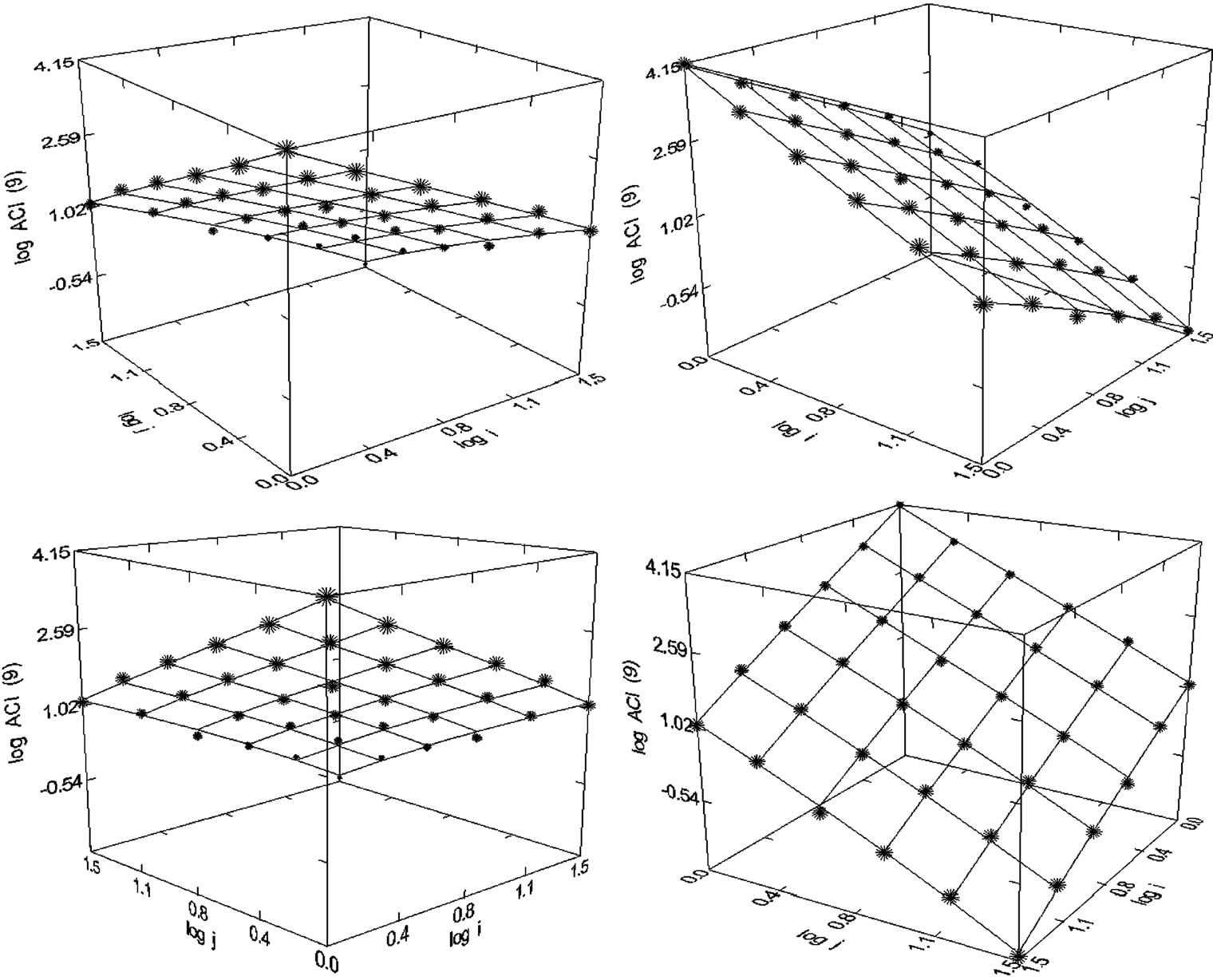
Figure 26. Angewandte Chemie International Edition (1980-1998), N = 36, R2 = 0.998, F-ratio = 4261.265, P = 0.000, NT = 52,880, Authors = 9716, Articles = 4668.

Figure 27. Science (1980-1998), N = 36, R2 = 0.998, F-ratio = 4338.546, P = 0.000, NT = 369,532, Authors = 47,161, Articles = 17,750.

Figure 28. Journal of the Neurological Sciences (1980-1998), N = 35, R2 = 0.997, F-ratio = 2408.529, P = 0.000, NT = 59,760, Authors = 8824, Articles = 3393.

Figure 29. Psychology of Women Quarterly (1976-2009), N = 16, R2 = 0.998, F-ratio = 1354.52, P = 0.000, NT = 4342, Authors = 2569, Articles = 1146 (Presented in [21]).
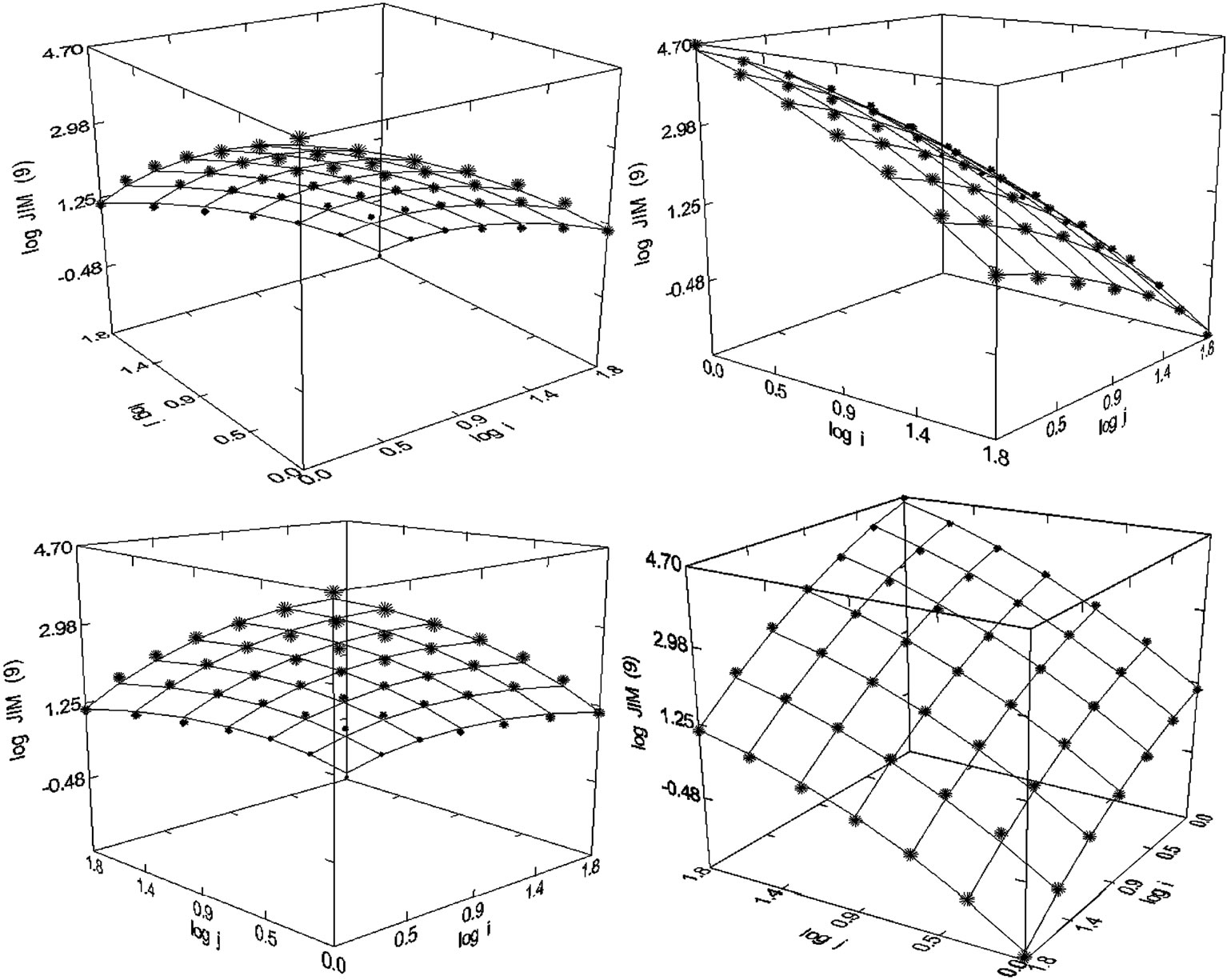
Figure 30. Journal of Immunology (1980-1998), N = 49, R2 = 0.997, F-ratio = 4205.985, P = 0.000, NT = 381,646, Authors = 42,728, Articles = 23,459.

Figure 31. Journal of Chemical Physics (1980-1998), N = 64, R2 = 0.997, F-ratio = 4931.713, P = 0.000, NT = 159,036, Authors = 29,726, Articles = 34,952.

Figure 32. Biochemistry-us (1980-1998), N = 49, R2 = 0.997, F-ratio = 4282.782, P = 0.000, NT = 298,586, Authors = 43,675, Articles = 27,441.
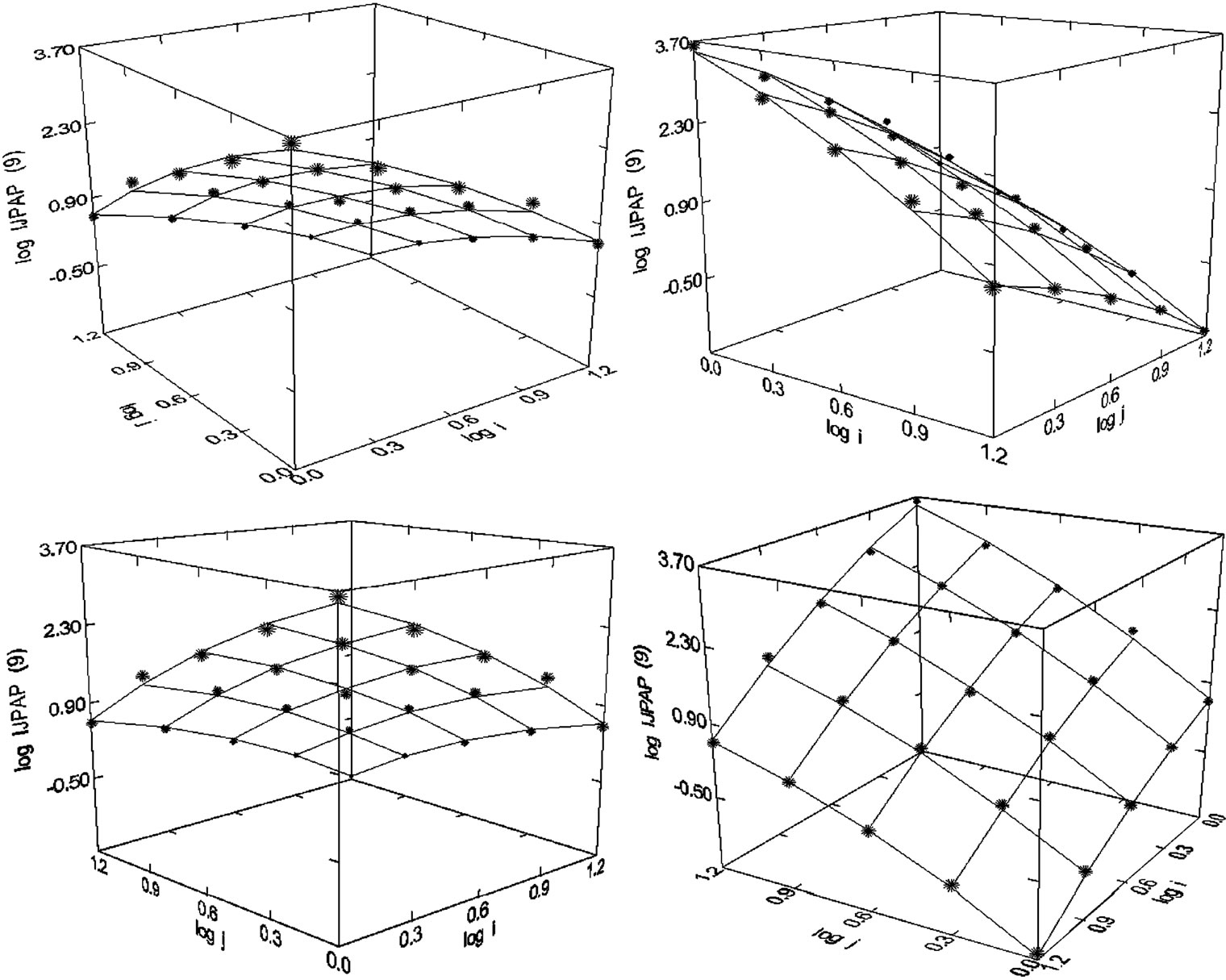
Figure 33. Indian Journal of Pure and Applied Physics (1997-2008), N = 25, R2 = 0.997, F-ratio = 1820.202, P = 0.000, NT = 12,950, Authors = 3251, Articles = 1721 (Presented in [23]).
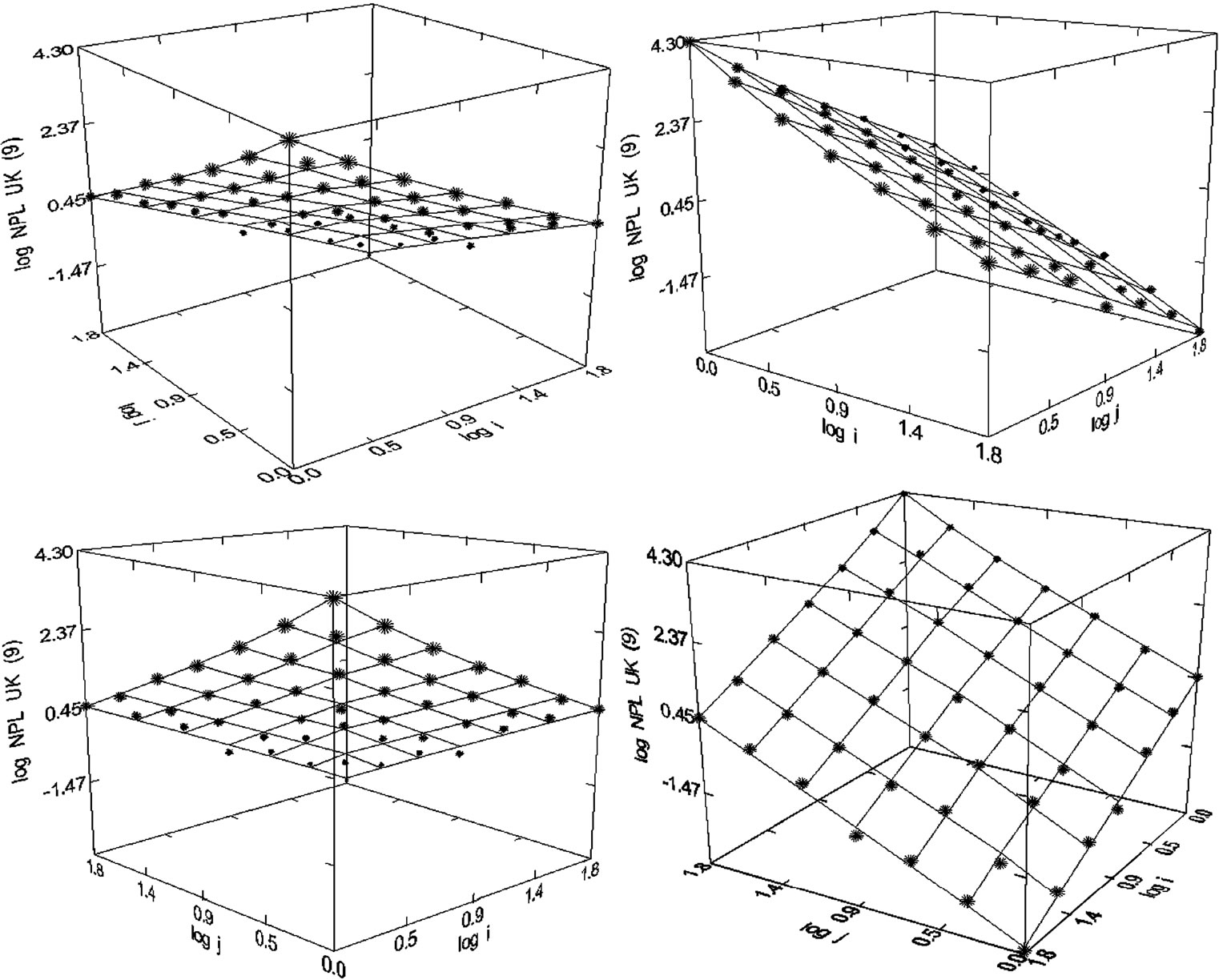
Figure 34. National Physical Laboratory UK, N = 49, R2 = 0.997, F-ratio = 3188.110, P = 0.000, NT = 55,132, Authors = 4021, Articles= 2045 (Presented in [23]).
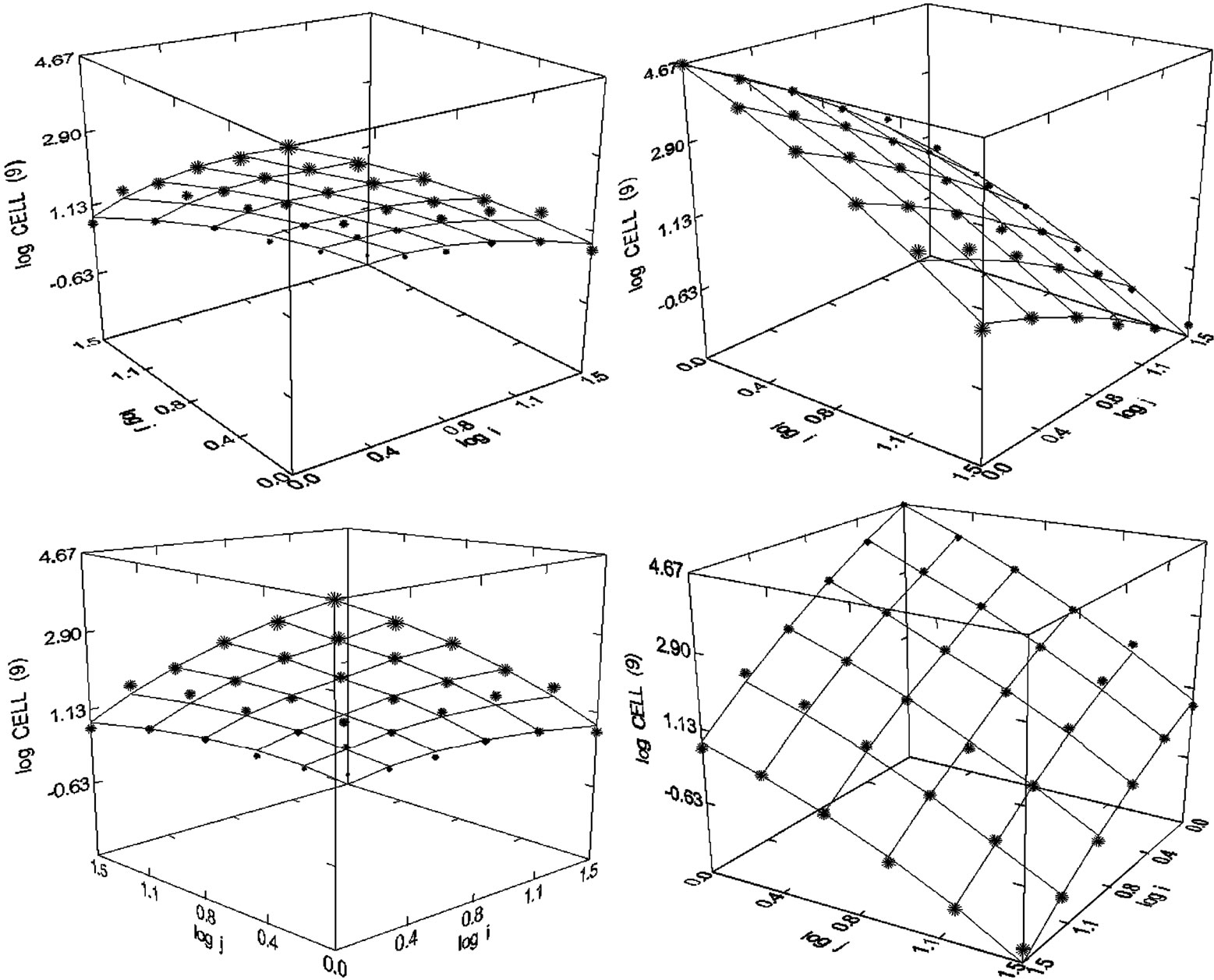
Figure 35. Cell (1980-1998), N = 36, R2 = 0.996, F-ratio = 1747.307, P = 0.000, NT = 147,398, Authors = 18,383, Articles = 7090.

Figure 36. Journal of the American Chemical Society (1980-1998), N = 63, R2 = 0.996, F-ratio=3643.006, P = 0.000, NT = 261,582 Authors = 39,029, Articles = 24,778.
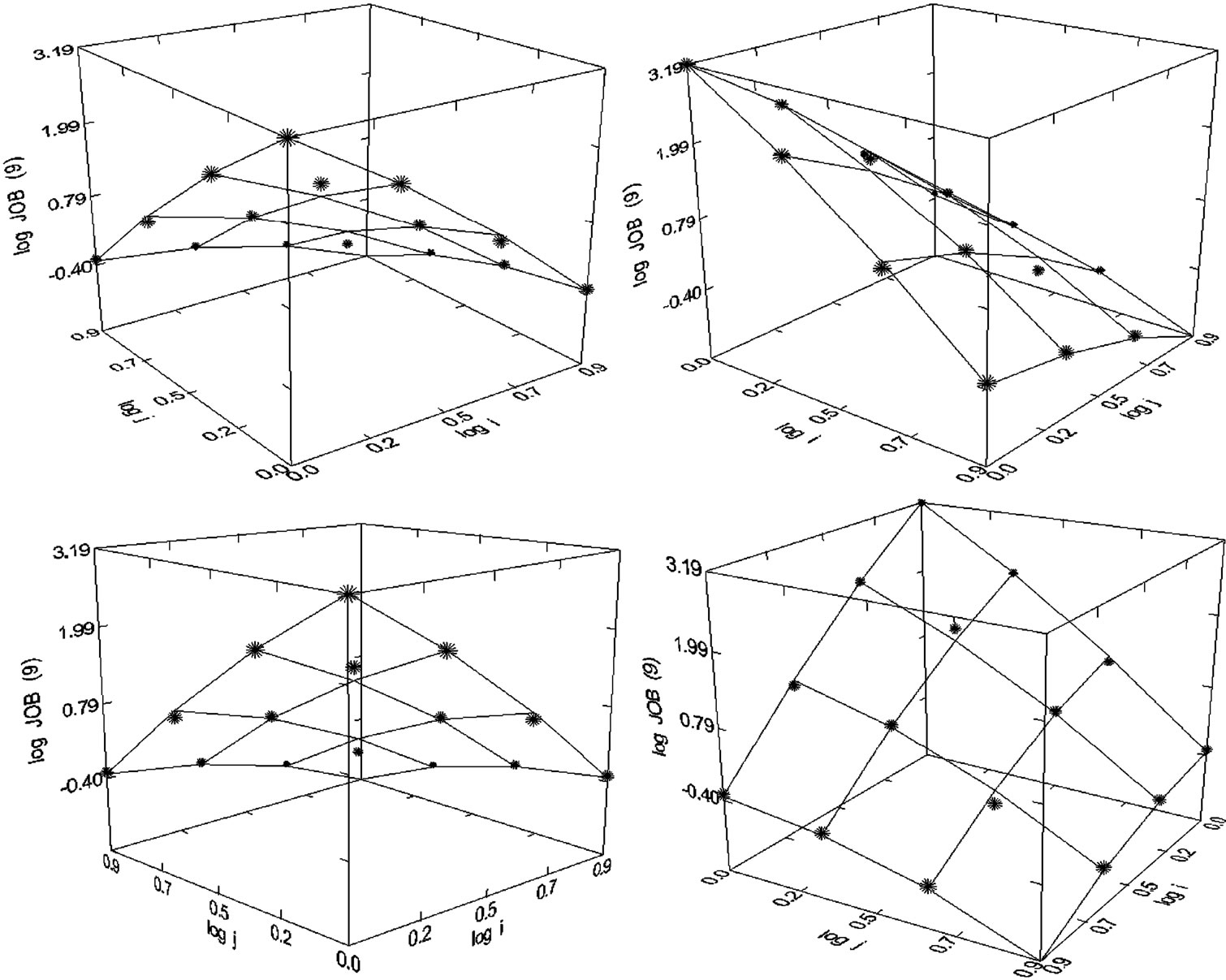
Figure 37. Journal of Experimental Medicine (1980), N = 15, R2 = 0.995, F-ratio = 482.793, P = 0.000, NT = 2504, Authors = 724, Articles = 260.

Figure 38. Circulation Research (1980-1998), N = 35, R2 = 0.995, F-ratio = 1494.6, P = 0.000, NT = 64,530 Authors = 10,098, Articles = 4320.
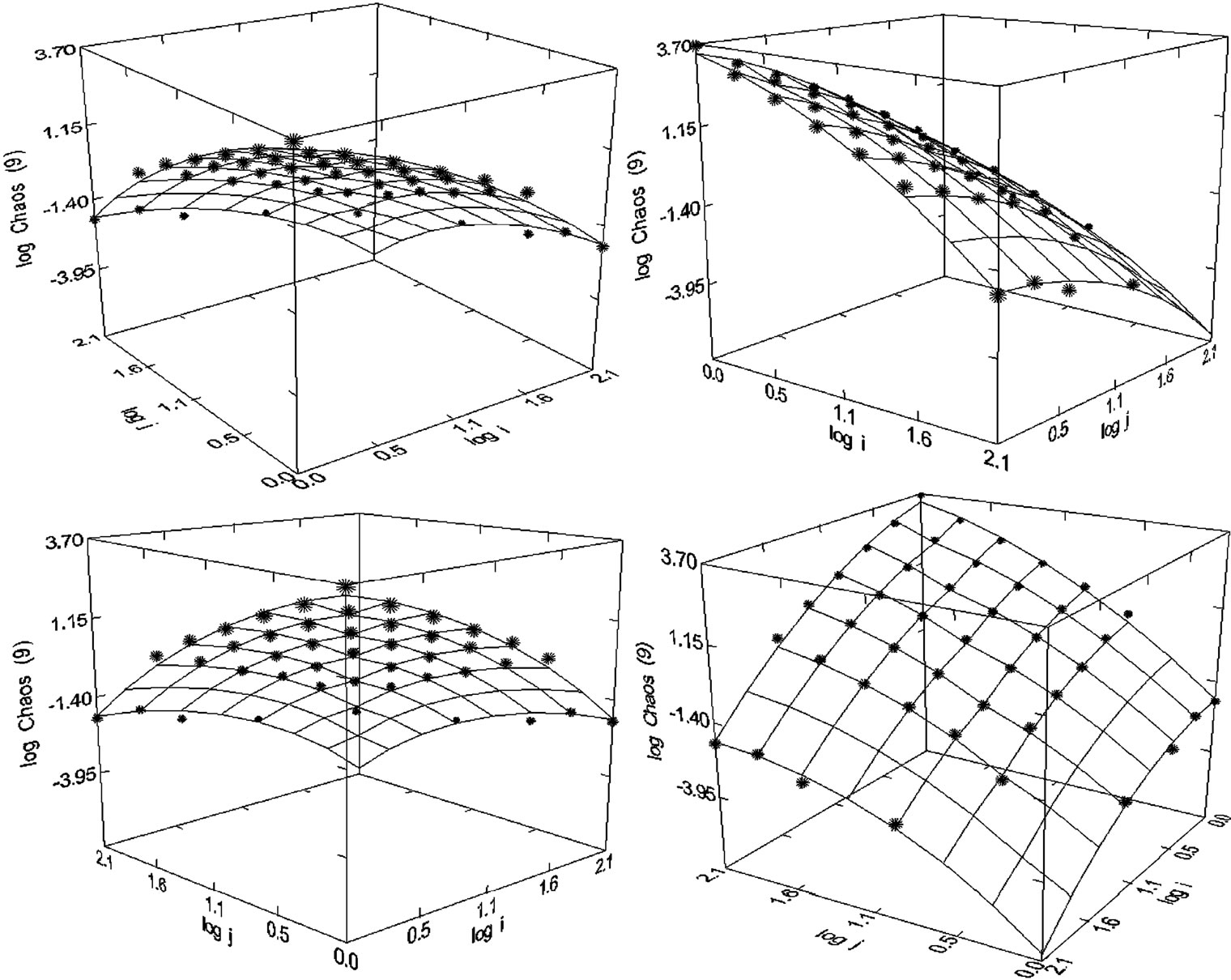
Figure 39. Chaos Solition Fractals (1993-2008), N = 44, R2 = 0.995, F-ratio = 1962.341, P = 0.000, NT = 16,688, Authors = 5681, Articles = 5936.
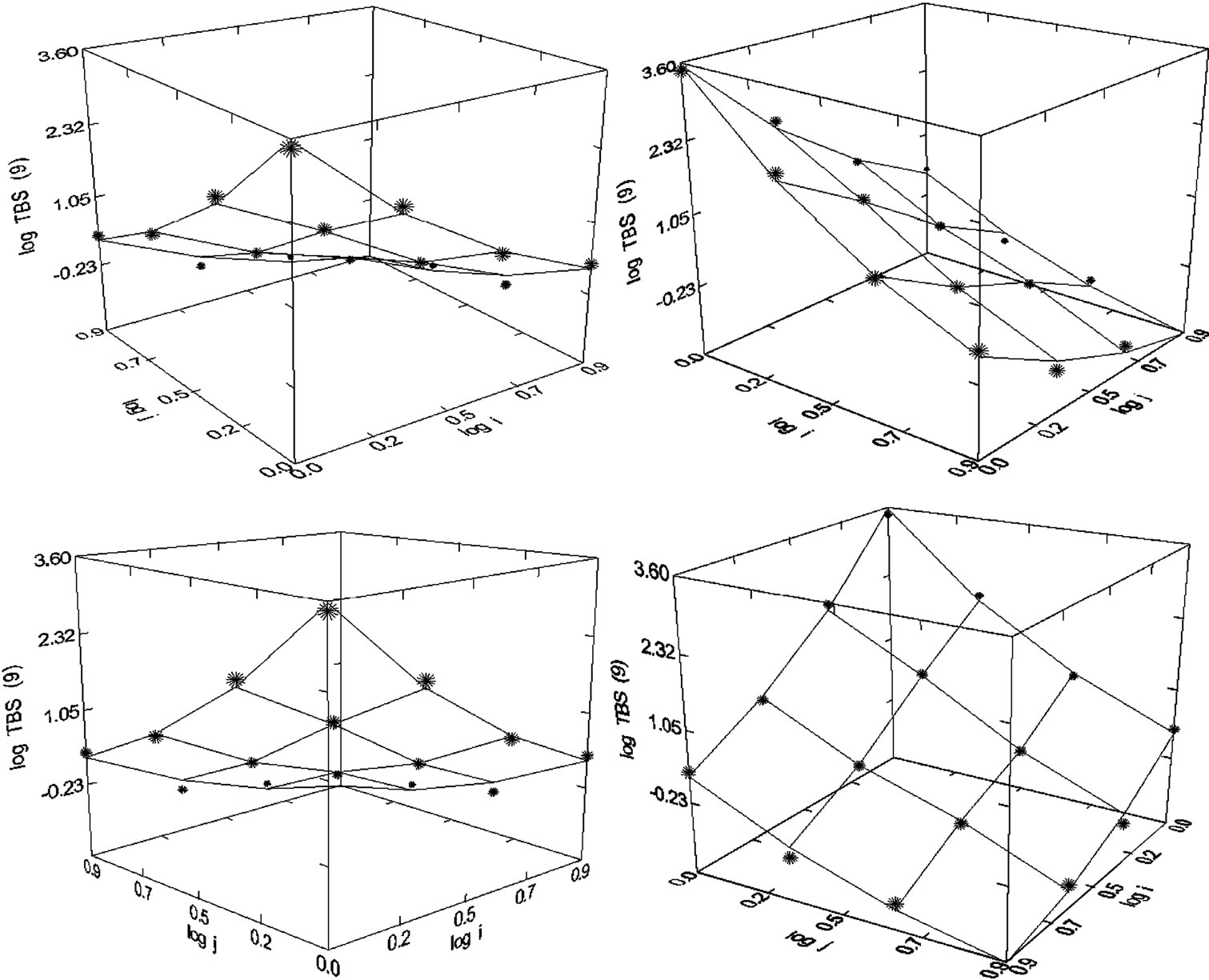
Figure 40. Trends in Biochemical Sciences (1980-1998), N = 15, R2 = 0.994, F-ratio = 418.142, P = 0.000, NT = 3730, Authors = 1725, Articles = 1148.
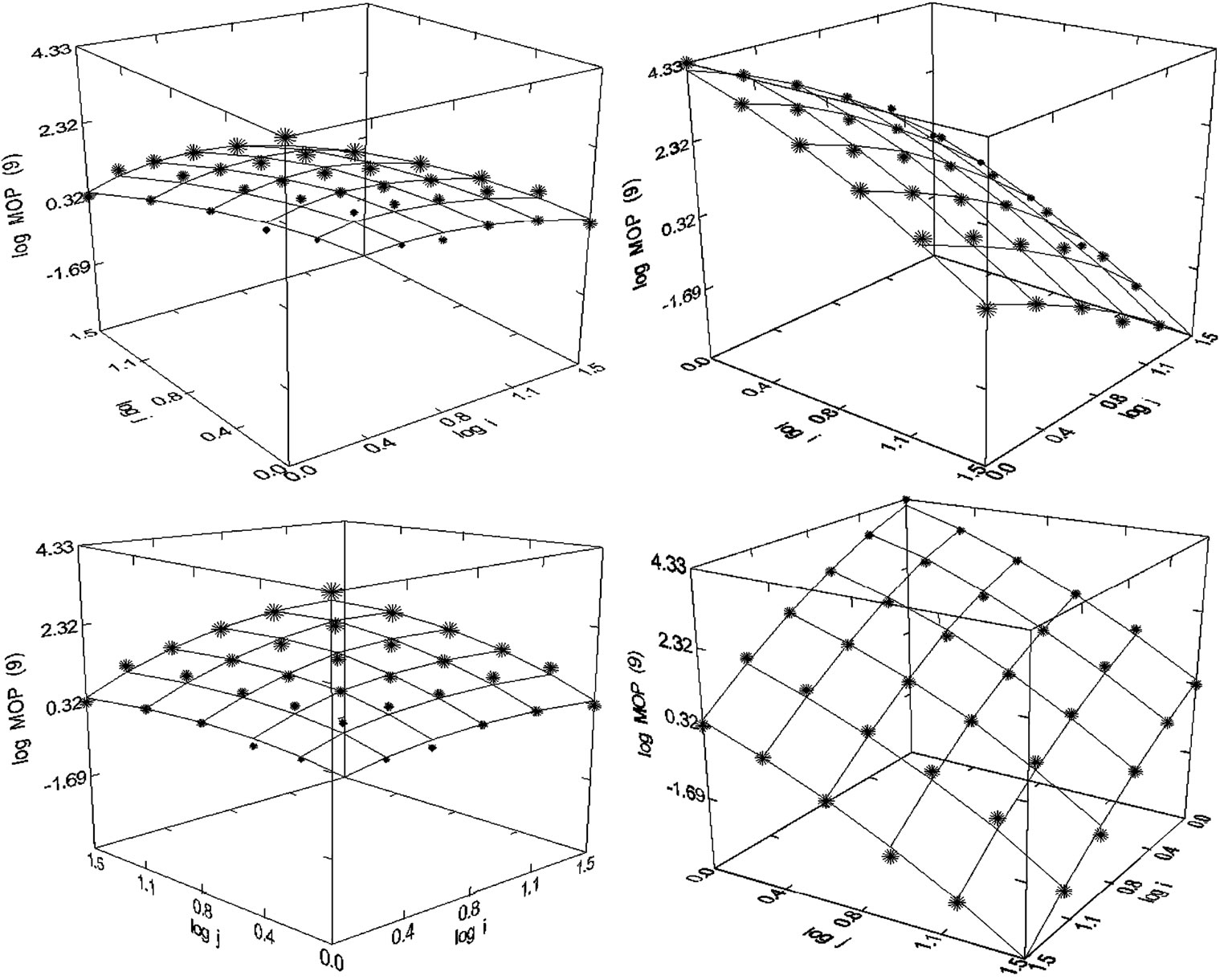
Figure 41. Molecular pharmacology (1980-1998), N = 35, R2 = 0.994, F-ratio = 1312.347, P = 0.000, NT = 63,522, Authors = 10,974, Articles = 4286.

Figure 42. Journal of Experimental Medicine (1980-1998), N = 36, R2 = 0.994, F-ratio: 1384.706, P = 0.000 NT = 133,852, Authors = 16,493, Articles = 5990.
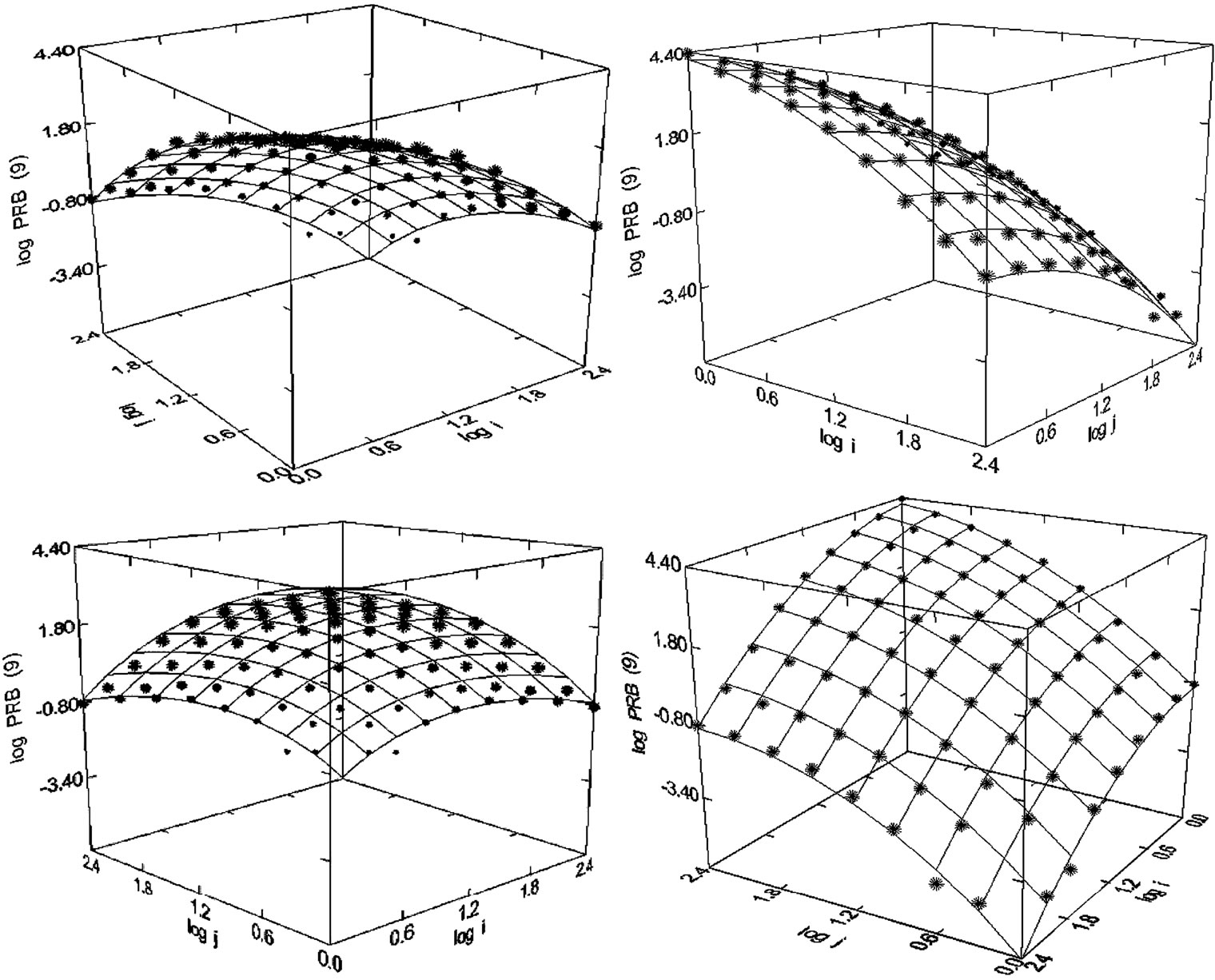
Figure 43. Physical Review B Condensed Matter (1980-1998), N = 79, R2 = 0.994, F-ratio: 3330.596, P = 0.000, NT = 382,218, Authors = 46,334, Articles = 49,392.
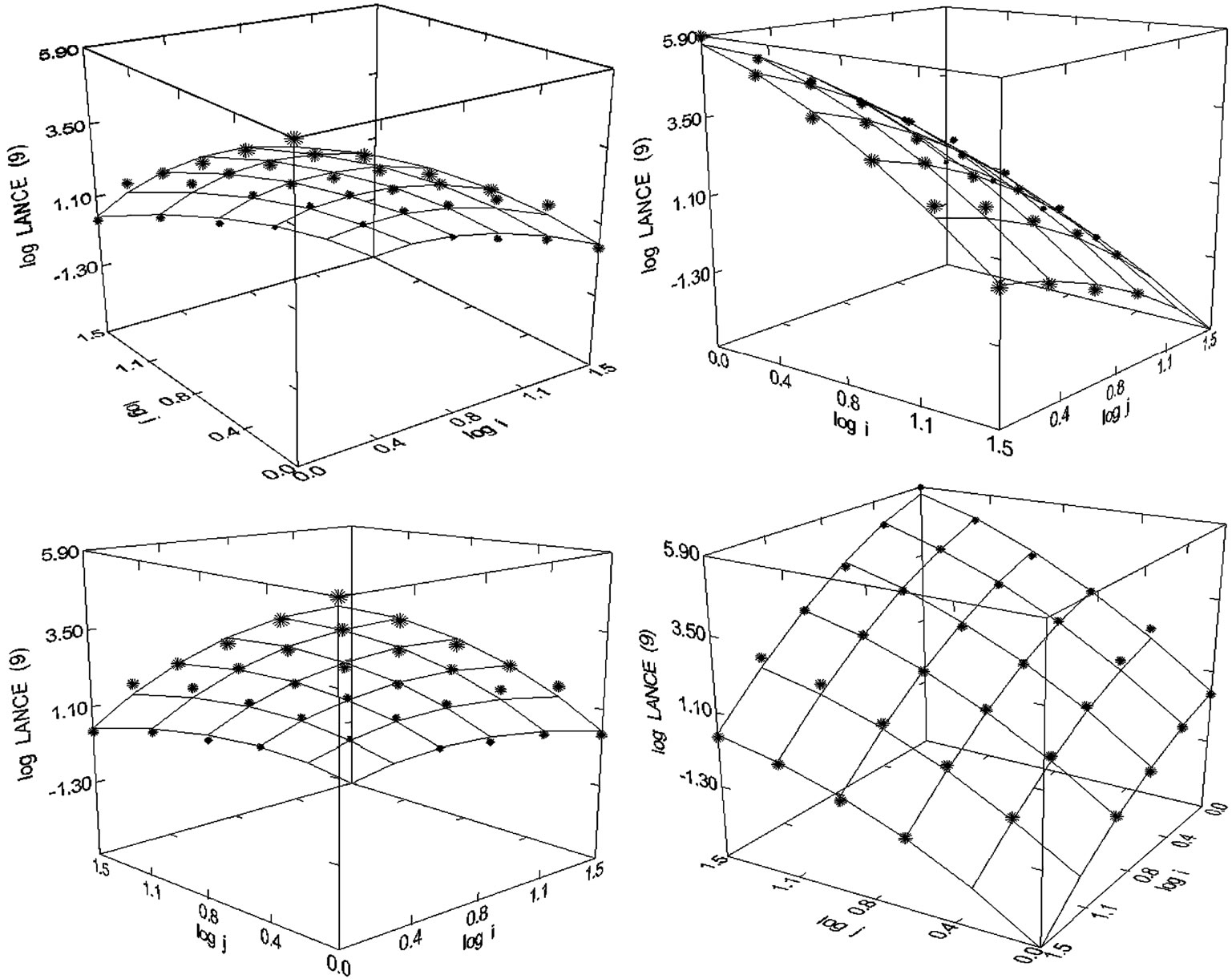
Figure 44. Lancet (1980-1998), N = 33, R2 = 0.994, F-ratio = 1234.290, P = 0.000, NT = 1,469,670, Authors = 37,664, Articles = 9203.

Figure 45. Journal of the National Cancer Institute (1980-1998), N = 36, R2 = 0.993, F-ratio: 1074.490, P = 0.000, NT = 112,406, Authors = 13,936, Articles = 4338.
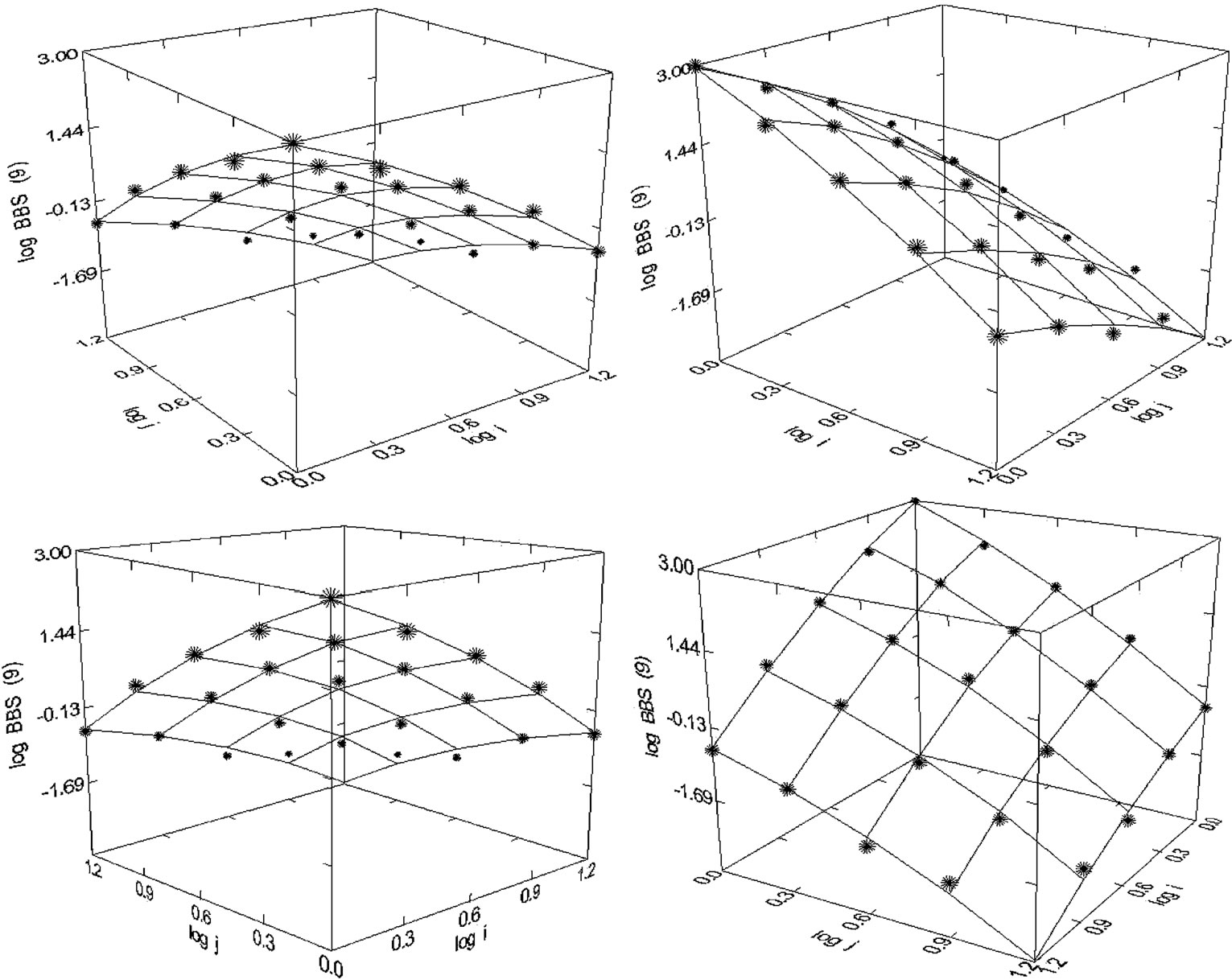
Figure 46. Behavioral and Brain Sciences (1980-1998), N =24, R2 = 0.993, F-ratio: 685.428, P = 0.000, NT = 2398, Authors = 3986, Articles = 5638, aut/art = 1:20.

Figure 47. Annals of Internal Medicine (1980-1998), N = 35, R2 = 0.993, F-ratio: 1025.810, P = 0.000, NT = 253,986, Authors = 13,609, Articles = 3268.

Figure 48. American Journal of Human Genetics (1980-1998), N = 35, R2 = 0.993, F-ratio = 1082.1, P = 0.000, NT = 197,788, Authors = 13,454, Articles = 3736.
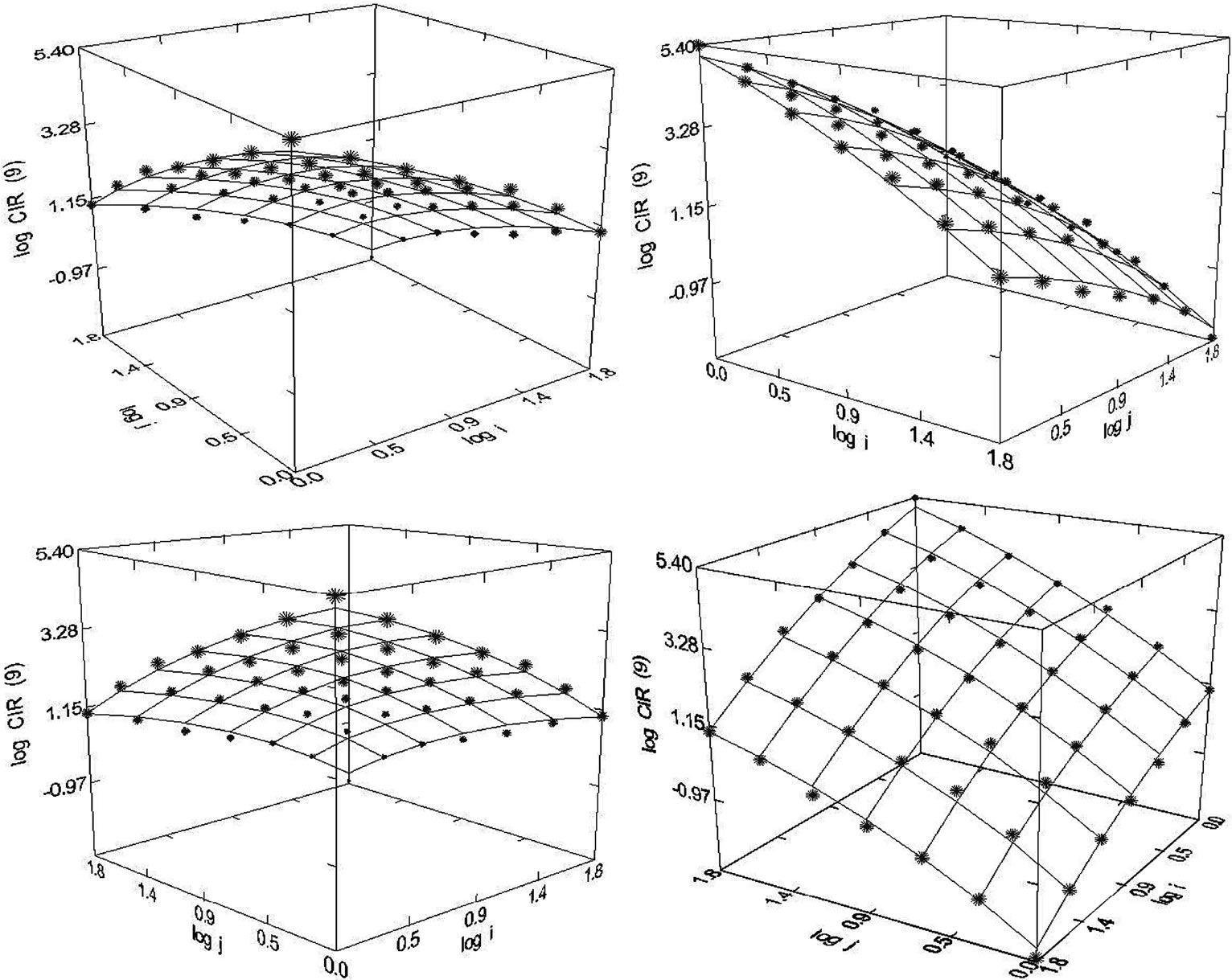
Figure 49. Circulation (1980-1989), N = 49, R2 = 0.993, F-ratio = 1660.771, P = 0.000, NT = 779,746, Authors = 29,587, Articles = 10,493.
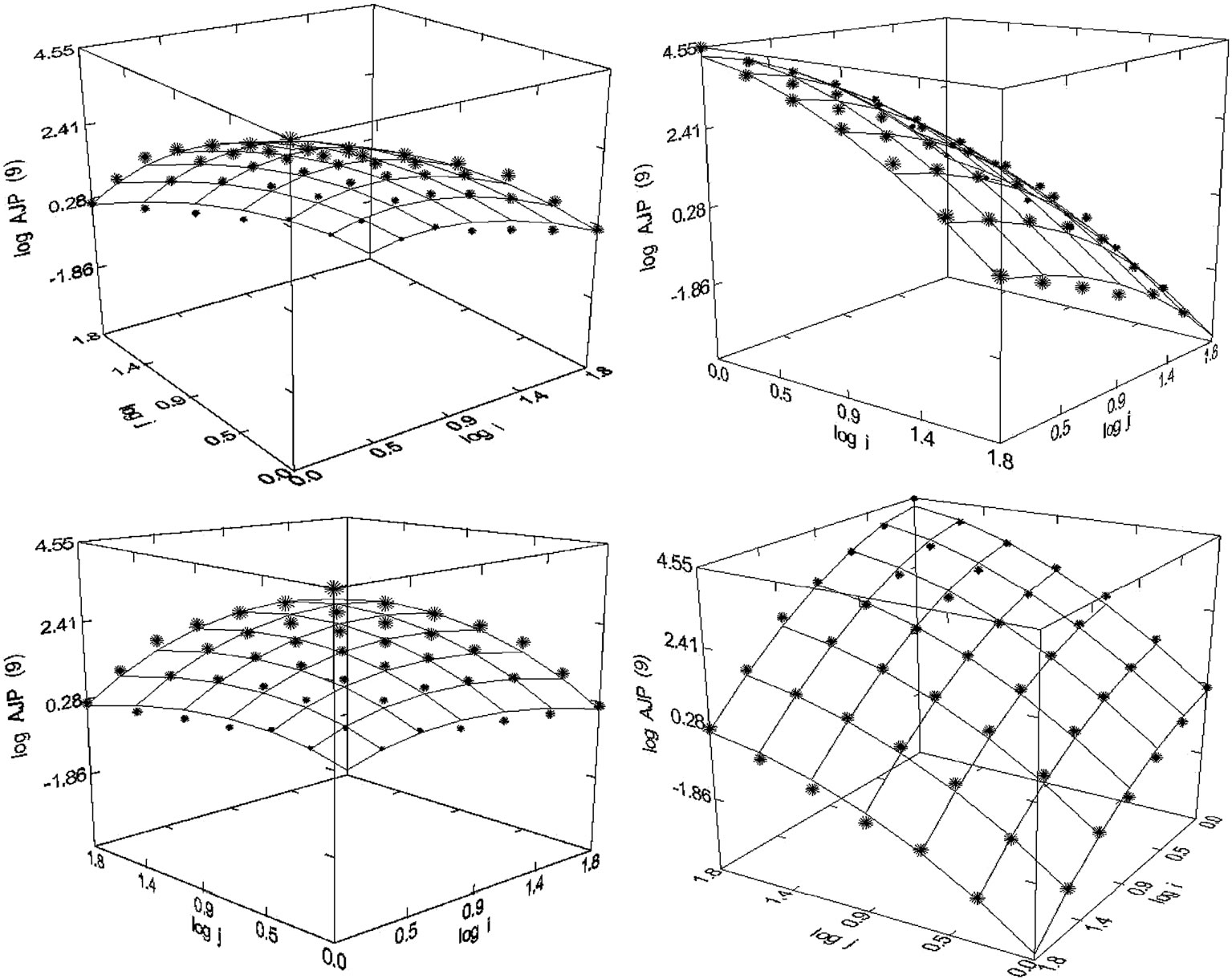
Figure 50. American Journal of Physiology (1980-1998), N = 48, R2 = 0.993, F-ratio: 1546.460, P = 0.000, NT = 206,098, Authors = 35,445, Articles = 23,061.
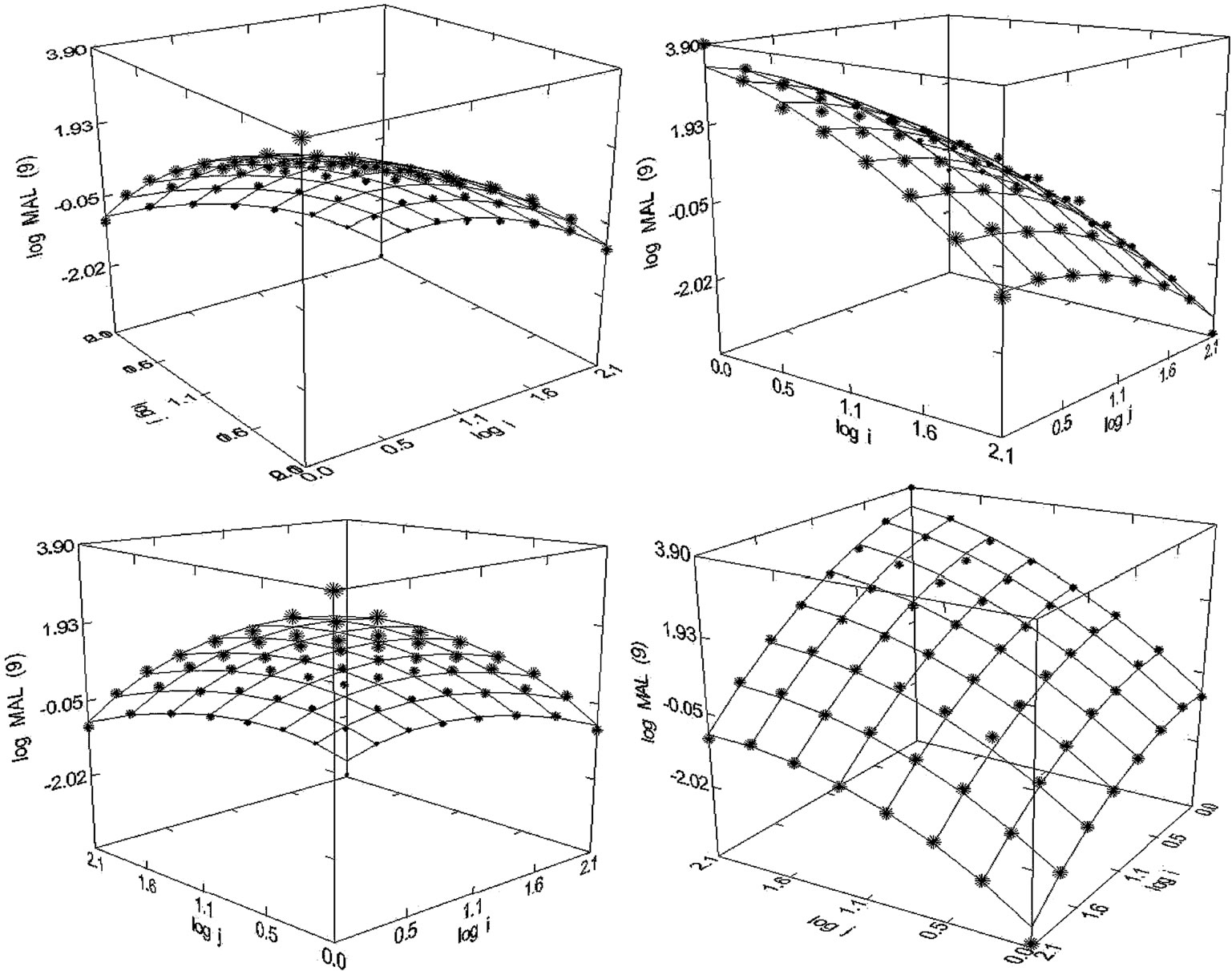
Figure 51. Malaria Research (1955-1995), N = 64, R2 = 0.993, F-ratio = 2117.983, P = 0.000, NT = 59,840, Aut = 12,227, Articles = 62,494.

Figure 52. Malaria Research (1996-2005), N = 64, R2 = 0.993, F-ratio = 2073.509, P = 0.000, NT = 147,032, Authors = 18,961, Articles = 57,019.
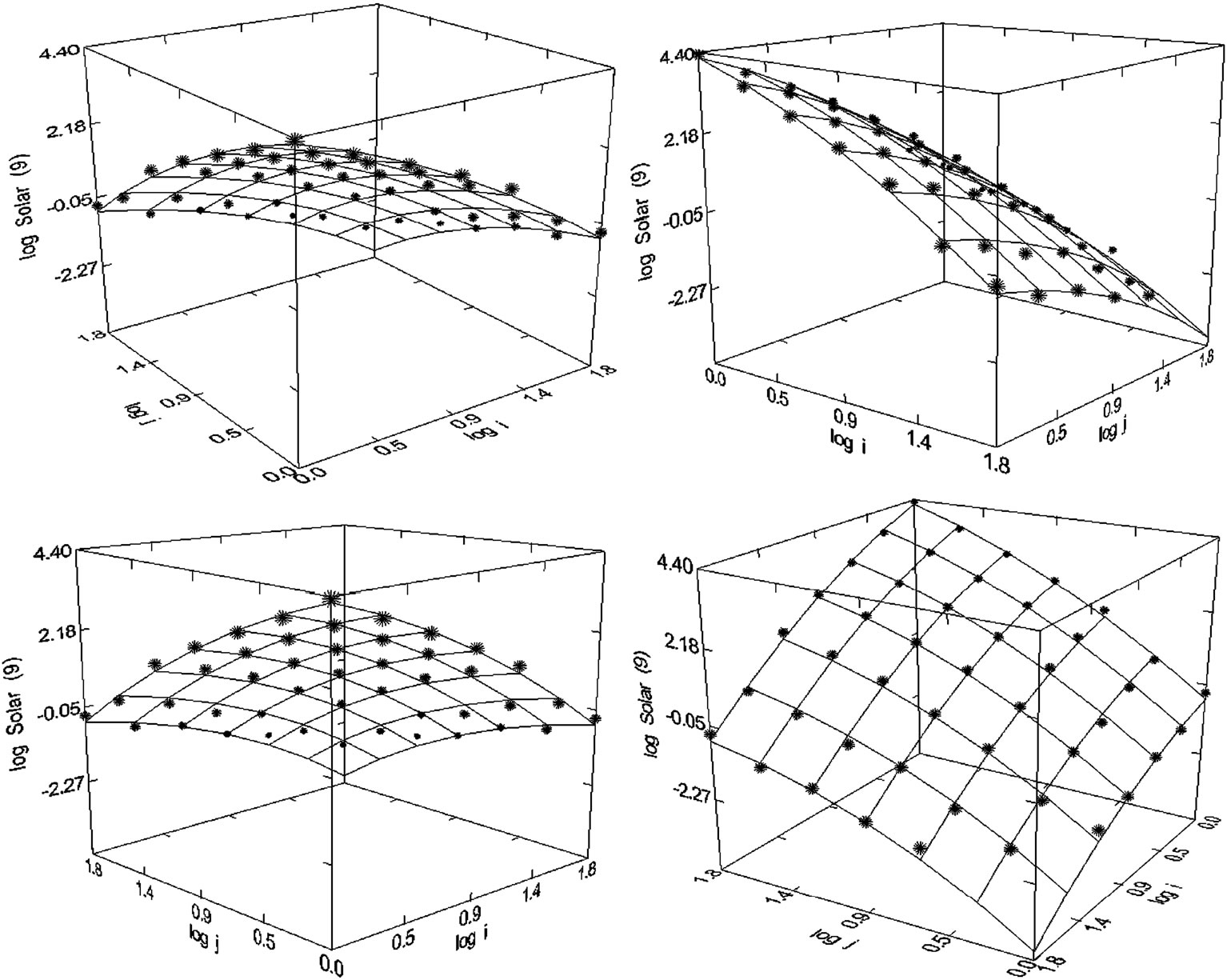
Figure 53. Solar Energy (1993-2008), N = 46, R2 = 0.993, F-ratio = 1548.343, P = 0.000, NT = 80,964, Authors = 14,170, Articles = 7194 (Presented in [24]).
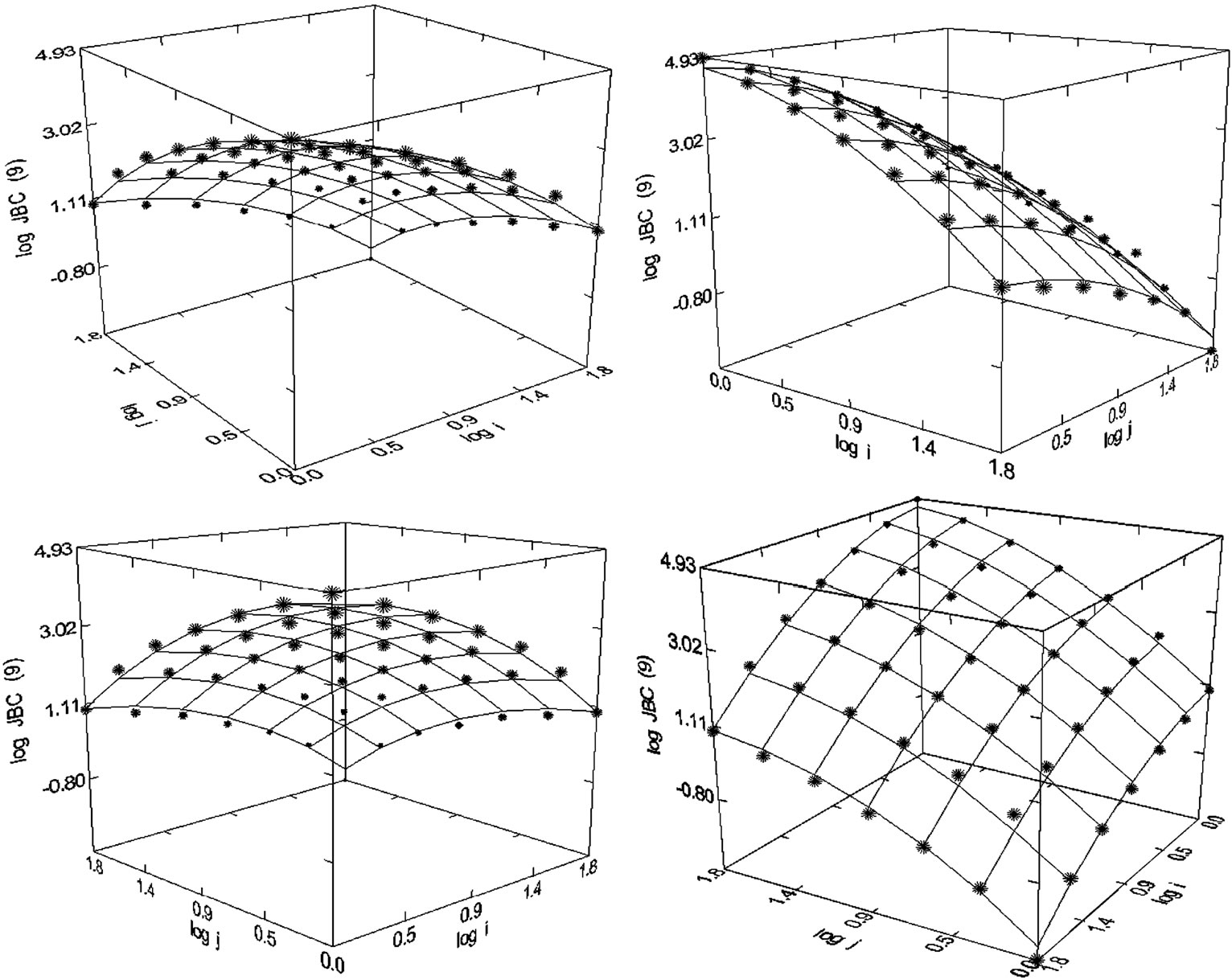
Figure 54. Journal of Biological Chemistry (1980-1998), N = 49, R2 = 0.992, F-ratio = 1443.952, P = 0.000, NT = 779,156, Authors = 96,136, Articles = 59,671.

Figure 55. Women’s and Gender Studies (1995-2007), N = 21, R2 = 0.992, F-ratio: 468.161, P = 0.000, NT = 6958, Authors = 6362, Articles = 5791 (Presented in [21]).
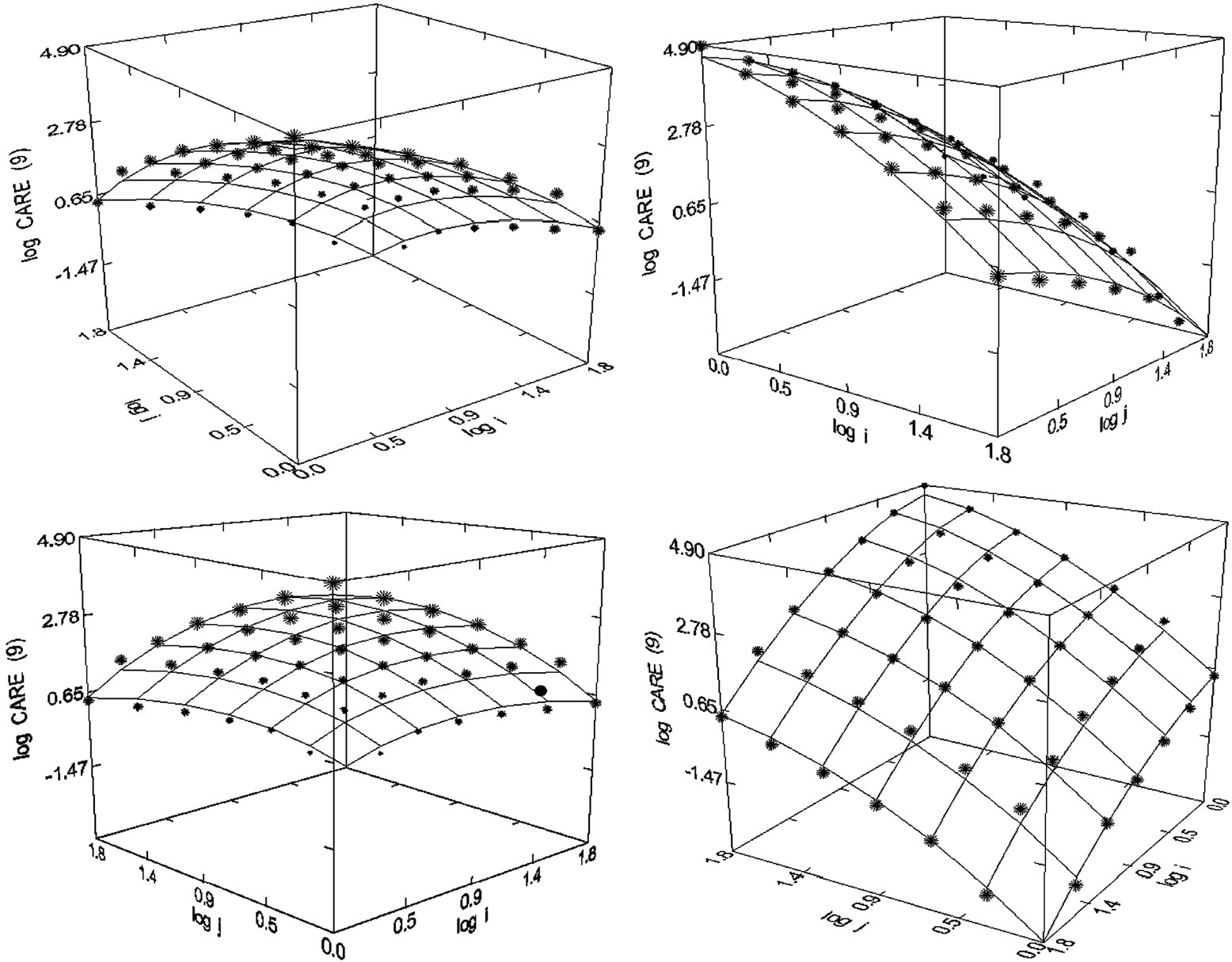
Figure 56. Cancer Research (1980-1998), N = 48, R2 = 0.991, F-ratio = 1252.064, P = 0.000, NT = 413,120, Authors = 45,029, Articles = 18,339.

Figure 57. Trends in Pharmacological Sciences (1980-1998), N = 17, R2 = 0.990, F-ratio = 303.904, P = 0.000, NT = 3278, Authors = 1724, Articles = 1241.
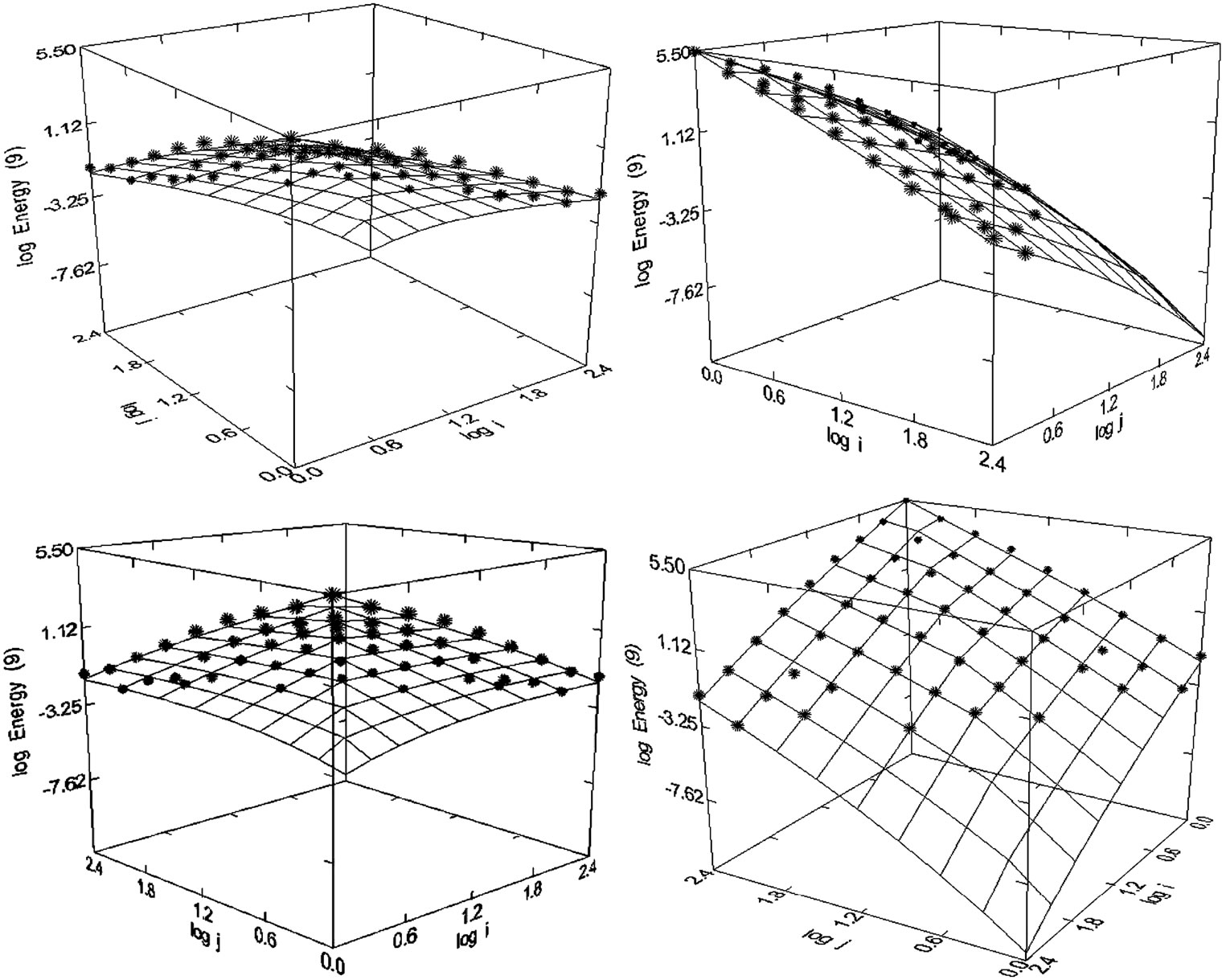
Figure 58. Energy Science and Technology (1993-2008), N = 54, R2 = 0.990, F-ratio = 1172.330, P = 0.000, NT = 624,072, Aut = 111,447, Article = 91,442 (Presented in [24]).

Figure 59. Journal of Experimental Medicine: Change of the shape over time from 1980 up to the period of 1980-1998 in total. First row: The two patterns from 1980 are taken from Figure 37 (bottom left and top right) with N = 15, R2 = 0.995, F-ratio = 482.793, P = 0.000, NT = 2504, Authors = 724, Articles=260; Second row: The two patterns obtained from the period 1980- 1998 are taken from Figure 42 (bottom left and top right) with N = 36, R2 = 0.994, F-ratio = 1384.706, P = 0.000, NT = 133,852, Authors = 16,493, Articles = 5990.

