International Journal of Medical Physics, Clinical Engineering and Radiation Oncology
Vol.04 No.03(2015), Article ID:57228,10 pages
10.4236/ijmpcero.2015.43024
Commissioning and Optimization of a Total Skin Electron Therapy Technique Using a High Dose Rate Electron Facility
Y. A. M. Yousif*, Casper A. Willemse
Medical Physics Department, Faculty of Health Sciences, University of the Free State, Bloemfontein, South Africa
Email: *Yousif.medphy@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 April 2015; accepted 13 June 2015; published 17 June 2015
ABSTRACT
Total skin electron therapy (TSET) is used for the treatment of Mycosis Fungoides. Several techniques have been developed, in order to achieve homogeneous dose distribution over the complete body surface. To implement a TSET technique, one has to optimize a variety of parameters. Monte Carlo simulation of TSET can facilitate this optimization. The aim of this study was to commission and optimize a TSET technique using the 4 and 6 MeV electron and the high dose rate facility on the Elekta Precise accelerator. The EGS4nrc/BEAMnrc Monte Carlo code was used. The beam data were calculated and measured at two different scoring planes for a single beam. The Model was validated by comparing the simulation with measurements. Two different vertical angles were used to obtain a uniform dose. The angle was optimized for best dose uniformity. The Rando phantom is placed on a rotating platform and rotates 60 degrees apart to facilitate the six patient position orientations. The doses delivered in a phantom by complete treatment were measured with Kodak EDR2 films and TLDs. The dose distribution varied among various scanning directions by 2 - 3 mm and 3 - 4 mm for 4 and 6 MeV respectively. The composite percentage depth dose of all six dual fields for the 4 and 6 MeV yielded an R80 of ~4 mm and ~6 mm, respectively. Dose uniformity was ±6% for 4 MeV and ±5% for 6 MeV. The bremsstrahlung contamination was 0.9% - 1.3%. Good agreements were found with published literature and inline with international protocols.
Keywords:
Total Skin Electron Therapy, Mycosis Fungoides, High Dose Rate Electron, Monte Carlo Simulation

1. Introduction
Skin tumors, such as mycosis fungoides and cutaneous lymphomas, are often treated with nitrogen mustard and Photo Ultra Violet type-A (PUVA) [1] , but the most effective treatment is Total Skin Electron Therapy (TSET) [2] -[4] . TSET was initially developed by Stanford University in the 1950s, and it has been considered to be one of the best options for mycosis fungoides treatment as well as skin diseases [5] [6] . The technique aims to deliver a relatively uniform dose distributions over the entire surface of standing body at an extended distances (e.g. 350 cm), while maintain minimum X-ray contaminations and limited doses to Organ-At-Risks (OAR). This will remain a challenge to achieve, because of the irregular shape of the body, which will result in non-uniform dose distributions on the skin surface [5] [7] [8] [10] . For this reason, TSET is regarded as complicated technique, since it necessitates special methods and tools for performing the non-standard dosimeterical measurements for evaluation and implementation. Monte Carlo (MC) simulation can facilitate such problem because of its accuracy and efficiency in estimating the radiation beam characteristics [9] [11] [12] . Thus, in order to achieve reliable results a powerful computing facility is needed as well as an experience is required although fields greater than 30 × 30 cm2 are not commonly used in the clinic. However, recently many studies using MC simulations cover electron beam commissioning of these large fields [9] [14] [15] . MC simulation for TSET has been investigated by several authors [13] [16] [17] . Pavón et al., demonstrated the capability of MC simulations to evaluate the beam properties of the TSET unit [15] . Sung-Joon et al., used MC techniques for design a TSET beam using different scattering foils in order to achieve an optimal dose distribution [13] . Although MC simulation has been successfully used for TSET beam design and optimization, however, most of the above studies were limited to a single electron energy that produced by Siemens or Varian Linear accelerates. In general clinical implementation of TSET technique remains varied among institutions depending on the Linear accelerator type, bunker size, dosimetry equipment’s and patient support devices. This work aims to commission and optimize a TSET technique using 4 and 6 MeV electron beams using MC simulation. The dosimetric procedure intends to obtain adequate dose uniformity over the entire surface of the patient, and to reduce the patient treatment time using a high dose rate facility on the Elekta Precise accelerator.
2. Materials and Methods
2.1. Introduction
At the Radiation Oncology department, National Hospital, University of the Free State, Bloemfontein, South Africa, the TSET technique is used for the treatment of Mycosis Fungoides. Elekta Precise linear accelerator was used to produce 4 and 6 MeV electron beams, operating in the High Dose Rate Electron (HDRE) mode (1000 MU/min). On entering the HDRE treatment mode, the X-ray collimators are automatically set to the maximum open position (40 × 40 cm2) [18] . The distance from the isocentre of the accelerator to the treatment plane was 350 cm (see Figure 1). A scatter plate of thickness of 0.5 cm was placed 20 cm to degrade the electron beam to obtain the required depth dose curve. A costumed-made rotating platform with a circular standing area of 60 cm diameter was fabricated in our departmental workshop to facilitate patient setup under the treatment conditions. The treatment is
Figure 1. (a) Shows a picture of the treatment room showing the Elekta Precise machine and the positioning of the Rando phantom at the treatment plane; (b) Geometrical arrangements of the symmetrical dual-field.
to be delivered from six equally spaced patient orientations by rotating the patient through 60 degrees after each stationary beam had been delivered. The treatment length will be encompassed by irradiating from two different vertical angles. In order to commission the TSET technique, it was necessary to determine the characteristics of the beams at the isocenter and at the treatment plane. Since we intended to use MC simulation in the commissioning of the TSET technique, the first step was to match the MC simulation data with the measured data for a single horizontal beam. MC simulation for the linear accelerator head was done to obtain the beam data for the 4 and 6 MeV electrons. The BEAMnrc code was used for the simulation of the accelerator and analysis of the data files [19] . The DOSXYZnrc and the CTCREATE MC codes were used for the calculation of the 3D dose distributions in the water phantom and CT based patient models [20] [21] . The beam data obtained by the DOSXYZnrc code in the water phantom was verified by comparing it with data measured in a polystyrene phantom. The dose distributions obtained by MC simulation of the Rando phantom were directly compared with data measured with films and TLD dosimeters.
2.2. Beam Data Measurements
Relative PDDs and beam profile measurements at the isocenter were made with the gantry at 0˚, and at the treatment plane with the gantry at 90˚. Measurements were done in a Solid water phantom with both a SHM (SHM Nuclear) parallel-plate ionization chamber connected to a Keithley 602 (Keithley) solid-state electrometer, and with Kodak EDR2-film. For the film measurements, a calibration curve was established to convert the optical density to dose [22] . The PDDs were obtained by irradiating unpackaged film edge-on in a RMI solid water film cassette (Gammex RMI), and using a Wellhöfer WP102 scanning densitometer with WP700 software (Wellhöfer Dosimetrie, Nuremburg, Germany). Beam profiles measured at dmax at the treatment plane, the phantom with the ion chamber was positioned vertically (at isocenter height) at the treatment plane, and then moved to different positions horizontally, perpendicular to the central axis.
2.3. Multiple Field Measurements
The TSET technique chosen was similar to the modified Stanford technique [5] , but with optimization of the gantry angles used for the dual fields. Film was used to determine dose distributions from multiple beams. Two phantoms were used: a cylindrical Perspex phantom with a diameter of 30 cm, and a Rando anthropomorphic phantom. Figure 1(b) shows the geometrical arrangements of the dual-field. The bare film was placed between selected Rando phantom slices at three different levels namely, chest, navel and pelvis level. The films were cut flush to the phantom surface, and sealed with two layers of black electric insulation tape in the dark room. The phantoms were positioned upright on a rotating platform at the treatment plane. Six irradiation directions at 60 degree intervals were achieved by rotating the platform. At each phantom orientation, a pair of fields was delivered at gantry angles of 104˚ and 76˚ for 4 MeV and at 106˚ and 74˚ for 6 MeV respectively. Thus at each energy a total of 12 fields were delivered at 200 MU per field. After irradiation, the PDDs and isodose curves were determined. When six pairs of TSET beams are delivered in patient treatments, the dose delivered to any point on the patient surface will be larger than what would have resulted from a single beam pair, due to the overlap of adjacent beam pairs. The ratio of the dose delivered to the skin by the six beam pairs treatment to that delivered at dmax by a single TSET beam pair, given the same MU per beam, is defined as the overlap factor [5] [23] [24] . An accurate determination of the overlap factor is important in TSET dosimetry as it determines the MU per beam for a given prescribed skin dose. The overlap factor for our technique was measured at the level of the horizontal beam axis by using both film and TLD. Once the overlap factor was determined, the MU needed to give a prescribed skin dose with the TSET treatment was calculated. Using the calculated MU for the complete TSET irradiation of the Rando phantom, doses to other anatomic locations were measured using TLDs.
For in-vivo dosimetry, the TLDs were taped to the surface of the Rando phantom at the chosen levels for the six beam pair irradiation. To minimize the statistical uncertainty, three TLD chips were placed at each anatomic location. Measurements were performed according to an established procedure or protocol in our department. For the absolute dosimetry, a plane-parallel ionization chamber has been used (according to the AAPM report No. 23 recommendations) [5] for measuring the depth dose distribution. The calibration depths were measured from the depth dose curves for the 4 and 6 MeV. The X-ray contamination was measured from the tail of the depth dose curves according to the accepted method [5] [23] [24] .
2.4. Monte Carlo Simulation
MC simulation was used for modeling of the radiation head of an Elekta Precise linear accelerator. The construction details of the treatment head were provided by the manufacturer. Figure 2 shows a schematic of the head for 4 and 6 MeV electron beam configuration mode. Our EGSnrc/BEAMnrc simulations consisted of two stages; the first stage involved adjusting the primary electron beam parameters to match the beam data measured at the isocenter (100 cm SSD). In the second stage, these beam parameters were used to compute dose distributions at the treatment plane (350 cm SSD). In the first stage of the simulation, ten component modules (CMs) were used. The 700 icru cross-section data for materials as stated in the PEGS4 data file were used with additional materials had to be added to the PEGS data file for modeling all accelerator components correctly. Monoenergetic pencil beams of 4 and 6 MeV electrons were directed at the electron exit window. Initially 100 million histories were used to generate the electron beams. The electron cut-off (ECUT) and photon cut-off (PCUT) values were set at 0.7 MeV and 0.01 MeV respectively in all CMs. The PRESTA algorithm was set on during simulations, because that had proved to increase the history simulation rate quite effectively [14] . The number of histories was chosen so as to reduce the percentage error to less than two percent in all voxels in the field. This required about 600 million histories and the simulation rate was in the order of 7.5 × 107 histories per hour on our simulation facility. Simulation for the total phase space files (PSF) for the 4 and 6 MeV energies typically took 12 - 14 h and 13 - 16 h CPU time on our Windows based computers (see Table 1). To validate the
Figure 2. Schematic digram of the Elekta Precise linear accelerator showing the beam shaping components and the name of the associated Modules used for BEAMnrc simulations.
Table 1. Details of the calculations of the beam data from the PPSFs and SPSFs.
simulation parameters of the primary electron beam, published methods were used, and through matching our calculated PDDs and beam profiles to our measurements [13] [16] [17] . At first beam parameters for linear accelerator simulation from scientific literature were used, and then adjustment were made until the best match was establish. A parallel circular beams with different energies having Gaussian radial distributions of full width at half-maximum (FWHM) of 0.05 cm were used. The beam parameters that yielded the closest agreement between simulations and measurements were considered as the true beam parameters and used for all subsequent calculations. In the second stage transport of phase space particles from isocentre to the treatment plane was simulated. Here the electron beam parameters as used in the first stage were maintained. Bremsstrahlung splitting, Russian roulette or photon forcing were not used. The simulation in this stage resulted in a short simulation time compared with the first stage, because just the air gap component module was modeled. The BEAMDP code and evaluated to evaluate the planar energy fluence from the PSFs data.
An EGSnrc user code, DOSXYZnrc [19] was used to calculate dose distributions. The generated PSFs were used as source input files for the DOSXYZnrc code [20] . For the beam data calculation two water phantom models were constructed: one at the isocentre and the other at the treatment plane. The isocentre and the treatment plane were made to coincide with the isocenter for the DOSXYZnrc simulation at the surface of the water phantom for each. These phantoms were constructed in such a way that the X by Y by Z dimensions were 200 × 100 × 24 cm3 and 400 × 200 × 24 cm3 respectively. The doses in the region of interest were scored in voxels of 2.0 cm × (length) × 0.5 cm (width) × 0.25 cm (depth) for both phantoms. The output file generated by DOSXYZnrc consists of a 3D dose array, and PDDs and beam profiles were calculated and compared with similar data obtained by measurements.
For MC simulation on Rando Phantom, a CTCREAT program was used, it is a CT phantom option of DOSXYZnrc that allows calculation of dose distributions in phantoms that are derived from CT data sets. A CT scans of a Rando phantom were made on a Siemens Somatom HiQ-S CT scanner. Before the data can be used directly for dose computation, they have to be converted to electron densities relative to that of water. Here the PSFs from the second stage of the simulation were used as a source for calculation of the dose distributions in CT based model using CT the CTCREATE program. The whole Rando phantom was irradiated using six dual fields in one session using a single beam source option of DOSXYZnrc. The dose distribution was analyzed for the different slices at the levels of the Rando phantom that corresponded with the film positions during the actual irradiation. The dose was normalized at the calibration point, which is located near to the skin at the navel level of the Rando phantom (according to the AAPM TG-32 protocol recommendation). A program was written in IDL (Interactive Data Language) [25] to read, normalize and display the dose distributions for MC simulation and film.
3. Results and Discussion
3.1. HDRE-Special Procedures Mode
The operating parameters including linear accelerator dose and dose rate with the collimator setting at its maximum for the HDRE mode were investigated. Table 2 shows the results of OF measurements for the two energies at isocentre and treatment plane. It can be clearly seen from the results that the dose rate at treatment plane in HDRE mode is comparable with the dose rate at isocentre in normal mode. The dose rate of the machine in HDRE mode at the isocentre is approximately ten times that in the normal treatment mode [18] . This is due to the decreasing effect of the inverse square law at larger SSDs, the influence of the variation of SSD over the patient skin surface is reduced.
We define the output factor of the machine in the high dose rate mode as follows:
Table 2. Output factors (OFs) for 4 and 6 MeV measured at the isocentre and at the treatment plane with the HDRE applicator. OFs are expressed relative to the dose at dmax at isocentre with a 10 × 10 applicator at normal dose rate (the set-up for normal beam calibration).
 (1)
(1)
where 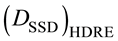 is the dose measured at the treatment plane in HDRE mode, for a single dual field, and
is the dose measured at the treatment plane in HDRE mode, for a single dual field, and 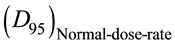 is the dose measured at the isocentre SSD, using a 10 × 10 cm2 applicator at normal dose rate.
is the dose measured at the isocentre SSD, using a 10 × 10 cm2 applicator at normal dose rate.
3.2. Beam Data Characteristics
The parameters characterizing the electron beam incident on the exit window were found by matching our calculated beam data to our measurements. For the measured beam data of 4 and 6 MeV energies we found the best match for the calculated beam data by using 5 and 6.72 MeV energies respectively. Figure 3(a) and Figure 3(b) show a comparison between the calculated and measured PDDs as well as beam profiles at isocentre and the treatment plane. The uncertainty of the simulation is less than 2%. The calculated values, of dmax, R50, and Rp agree with measured data within about 0.1 cm. This corresponds to about 3% change in dose. Both calculated and measured data were normalized to 100% at dmax. The average dmax is shifted from 0.95 to 0.78 cm and from 1.44 to 1.36 cm for the PDDs at the isocentre compared to that at the treatment plane for 4 MeV and 6 MeV respectively. The above results are consistent with other results reported in the literature [8] . Table 3(a) and Table 3(b) show a numerical comparisons between the calculated PDDs and measured data. Figure 2(b) shows comparisons of beam profiles calculated by MC and measured by ionization chamber and film. The calculated beam profiles agree with measurements within statistical uncertainties of 2%. The beam profiles for both energies at 100 SSD have a good uniformity and, this is probably due to the dual scattering foil design of the Elekta Precise machine [7] [8] [13] . For the dual field data the objective was to find the appropriate gantry angles that give a flat (±10%) profile over approximately1.8 m [5] . For TSET beams, we are helped by the fact that the beams are very broad and there is no distinct beam edge. By using a range of angles between the central axes of two beams, the angle that gave the best uniformity of dose was determined. Figure 4 shows the beam profiles calculated from combined beam profiles for the optimum angles. The optimized treatment fields were at 90˚ ± 14˚ for 4 MeV and 90˚ ± 16˚ for 6 MeV using beam scatter. The profile variations of a lower energy without using energy scatter plate are much greater than of 6 MeV with a scatter plate. The dose uniformity was ±6% for 4 MeV and ±5% for 6 MeV over the range of −120 to +80 cm.
3.3. Multiple Field Measurements
3.3.1. PDDs and Beam Parameters
Figure 5 shows PDDs measured in a cylindrical Perspex phantom for six-dual fields and for a single-dual field for 4 and 6 MeV at 350 SSDs. The PDDs for single-dual fields at the two different energies are obtained with the derived mean energies at the surface of the phantom. These curves correspond to the combined effect of two angulated beams on both sides of the horizontal axis for 4 and 6 MeV respectively. (These angles were the optimized values calculated from the MC simulations). The results of the single-dual fields were used to determine the position of the dose maximum (the calibration depth) for the absolute calibration. This was found to be 0.6 cm and 1.1 cm for 4 and 6 MeV energies respectively. The dmax values for the six-dual fields were found to be 0.2 and 0.3 cm and the R80 values were found at 0.64 cm and 0.91 cm for 4 and 6 MeV respectively. For X-ray

Figure 3. Show a comparison between the calculated and measured beam data at isocentre and the treatment plane.
Figure 4. Uniform beam profiles obtained from optimized angled fields at the treatment plane for 4 and 6 MeV.
Figure 5. Relative depth dose obtained with ion chamber for single dual field compared with the depth dose obtained with film in solid water phantom that is obtained with six-dual fields.
Table 3. (a) PDDs parameters at the isocentre; (b) PDDs parameters at the treatment plane.
contamination, the dual field technique reduces the total X-ray contamination at the center because the main bremsstrahlung component is on the central axis of the beam. The X-ray contamination was measured from the tail of the PDD curves and it was found to be 0.9% and 1.3% for the 4 and 6 MeV electron beam energies respectively.
The overlap factor; was determined from measurements with TLDs as well as film around the outer surface of the cylindrical phantom, and also from TLD measurements on the Rando phantom. Table 4 shows overlap factors (OV) measured with the different phantoms and dosimeters. For the Rando phantom the difference between prescribed dose and measured dose with TLD was about 4% as well as for the cylindrical phantom the difference was about 3.5%. These values are in good agreement with the literature [5] [23] .
For absolute dose measurements; the calibration depths were 0.6 cm and 1.1 cm for the 4 and 6 MeV respectively. These values correspond to the depth of maximum dose obtained from the depth dose curves in Figure 5 for a single dual field [5] . The mean energy of the beam,  , at the phantom surface (treatment plane) was determined by the half-value depth, R50, for a single-dual field. The R50 values are 1.38 and 2.2 cm for 4 and 6 MeV, thus the mean energies are 3.2 and 5.1 MeV for the 4 and 6 MeV beams respectively.
, at the phantom surface (treatment plane) was determined by the half-value depth, R50, for a single-dual field. The R50 values are 1.38 and 2.2 cm for 4 and 6 MeV, thus the mean energies are 3.2 and 5.1 MeV for the 4 and 6 MeV beams respectively.
3.3.2. Composite Dose Distributions
The obtained dose distributions from the complete treatment in the Rando phantom using the optimized beams are shown in Figure 6. The dose normalized relative to the calibration point, which is situated at the navel level, at depths of 0.2 and 0.3 cm for 4 and 6 MeV respectively. The results showed that the surface of the Rando Phantom have been completely covered by about 85% isodose curves using 4 and 6 MeV. Figure 7 shows comparisons between the measured PDDs and MC calculated PDDs obtained from the complete treatment using six dual-field. PDDs extracted from the complete six dual fields dose distribution at different levels (Chest, Navel and Pelvis) in the Rando phantom. The curves represent the PDD along the lines of intersection of the transverse planes at each level, and the plane containing the central axis of the two angled-fields incident from the anterior of the phantom. It can be noted that, for both methods the doses at the surface vary between 90 to 80% which is due to the effect of the overlapping beams from different angles of incidence. Also for both methods the dose distributions are higher in the areas that have sharp protrusions due to the larger degree of penetration and overlap of beams in those areas. Also the dose distribution shows some hot spots in the direction of 60 degree beam incidence which results from the overlapping of the fields. In general; the dose distributions for all
Table 4. Overlap factors.
Figure 6. A comparison of dose distributions around the skin surface at the navel level (normalized at the skin prescription point) for the film (a) and MC (b) for 4 MeV, film (c) and MC (d) for 6 MeV. The isodose lines are represented by 10 Percent = white, 30 percent = red, 50 percent = light blue, 70 percent = light green, 90 percent = dark blue and 100 percent = dark green.
Figure 7. Relative depth dose derived from the dose distribution (at three levels level) resulting from the complete six dual-field irradiation of a Rando phantom. Curves represent dose along a line in the plane containing the two anterior fields, and perpendicular to the surface of the phantom.
the above mentioned levels at the skin surface calculated by MC and film are very satisfactory.
4. Summary and Conclusions
The main purpose of this study was to commission and optimize a TSET technique for the treatment of mycosis fungiodes with the Elekta Precise linear accelerator using the HDRE mode that was installed on the machine. This was done through an extensive set of measurements and a large number of MC simulations. The MC beam models were validated by matching the simulated beam data at different scoring planes with corresponding measurements. By performing simulations for different dual beam gantry angles, the optimum gantry angles for acceptable beam uniformity over a large area at the treatment distance were obtained. The dose uniformity and the dose rate at the patient treatment plane are in a good agreement with the recommended protocol [5] , which was ±6% for 4 MeV and ±5% for 6 MeV over the range of −120 to +80 cm. The technique also reduces the treatment time while retaining proper functioning of all accelerator dosimetry systems. Moreover, the machine can be easily set up for treatment without additional technical support. The absolute calibration of absorbed dose to the patient requires the measurement of the ratio “skin dose to calibration point dose”. The value of this ratio was found to vary between 2.4 and 2.9 for the different dosimeters used in this study. These values were consistent with AAPM reported value (from 2.5 to 3) [5] . To assess the effective treatment depth and the degree of bremsstrahlung contamination, it is necessary to measure the PDD curves for the complete treatment using all twelve fields on a cylindrical phantom. From the results it can be concluded that the depth of maximum dose is approximately 2 and 3 mm and the therapeutic range (R80) is approximately 7 and 9 mm for the 4 and 6 MeV beam energies respectively. Therefore, the depth doses from multiple beams can indicate to the clinician the effective treatment depth.
The MC beam model developed in this work for the two energies of the accelerator in HDRE mode makes its possible in principle to calculate the dose distributions for individual patients, provided that a suitable anatomical model can be constructed for the patient in the actual treatment position. This could possibly be done by applying 3D optical reconstruction of the patient surface from multiple video frames acquired during a complete revolution of the treatment platform. This is currently being investigated as a possible follow up research project.
Cite this paper
Y.A. M. Yousif,CasperA. Willemse, (2015) Commissioning and Optimization of a Total Skin Electron Therapy Technique Using a High Dose Rate Electron Facility. International Journal of Medical Physics, Clinical Engineering and Radiation Oncology,04,197-207. doi: 10.4236/ijmpcero.2015.43024
References
- 1. Abel, E., Sendagrota, E., Hope, R. and Hu, H. (1987) PUVA TREATMENT of erthroderimic and Plaque-Type Mycosis Fungoides: Ten Year Follow-Up. Archives of Dermatology, 123, 897-901.
http://dx.doi.org/10.1001/archderm.1987.01660310065016 - 2. Maingon, P., et al. (2002) Radiotherapy of Advanced Mycosis Fungoides: Indications and Results of Total Skin Electron Beam and Photon Beam Irradiation. Radiotherapy and Oncology, 54, 73-78.
http://dx.doi.org/10.1016/S0167-8140(99)00162-0 - 3. Heserich, R., Richardoson, H. and Grant, J. (1990) Remission of Lesions in Mycosis Fungoides Following Topical Applications of Nitrogen Mustard. Cleveland Clinic, 26, 144-147.
http://dx.doi.org/10.3949/ccjm.26.3.144 - 4. Hope, R.T., et al. (1979) Electron-Beam Therapy for Mycosis Fungoides: The Stanford University Experience. Cancer Treatment Reports, 63, 691-700.
- 5. AAPM, American Association of Physicists in Medicine (1988) Total Skin Electron Therapy: Technique and Dosimetry. AAPM Report No. 23, American Institute of Physics, New York.
- 6. Khan, F.M. (2003) The Physics of Radiation Therapy. 2nd Edition, Williams & Wilkins, Maryland.
- 7. So-Yeon, P., Beom, A.I., Jong, M.P., Sung-Joon, Y., Il, H.K. and Jung-in, K. (2014) Dosimetric Comparison of 4 MeV and 6 MeV Electron Beams for Total Skin Irradiation. 197.
- 8. Lucic, F., Beatriz Sánchez-Nieto, B., Paola Caprile, P., Zelada, G. and Goset, K. (2013) Dosimetric Characterization and Optimization of a Customized Stanford Total Skin Electron Irradiation (TSEI) Technique. Journal of Applied Clinical Medical Physics, 14, 1-12.
- 9. Faddegon, B.A., Perl, J. and Asai, M. (2008) Monte Carlo Simulation of Large Electron Fields. Physics in Medicine Biology, 53, 1497-1510.
http://dx.doi.org/10.1088/0031-9155/53/5/021 - 10. Chen, Z., Agostinelli, A.G., Wilson, L.D. and Nath, R. (2004) Matching the Dosimetry Characteristics of a Dual-Field Stanford Technique to a Customized Single-Field Stanford Technique for Total Skin Electron Therapy. International Journal of Radiation Oncology * Biology * Physics, 59, 872-885.
http://dx.doi.org/10.1016/j.ijrobp.2004.02.046 - 11. Faddegon, B., Balogh, J., Mackenzie, R. and Scora, D. (1988) Clinical Considerations of Monte Carlo for Electron Radiotherapy Treatment Planning. Radiation Physics and Chemistry, 53, 217-227.
http://dx.doi.org/10.1016/S0969-806X(98)00103-0 - 12. Ma, C.-M. and Jiang, S.B. (1999) Monte Carlo Modeling of Electron Beams from Medical Accelerators. Physics in Medicine and Biology, 44, 157-187.
http://dx.doi.org/10.1088/0031-9155/44/12/201 - 13. Ye, S.-J., Pareek, P.N., Spencer, S., Duan, J. and Brezovich, I.A. (2005) Monte Carlo Techniques for Scattering Foil Design and Dosimetry in Total Skin Electron Irradiations. Medical Physics, 32, 1460-1468.
http://dx.doi.org/10.1118/1.1924368 - 14. Antolak, J.A., Bieda, M.R. and Hogstrom, K.R. (2002) Using Monte Carlo Methods to Commission Electron Beams: A Feasibility Study. Medical Physics, 29, 771-786.
http://dx.doi.org/10.1118/1.1469626 - 15. Bieda, M.R., Antolak, J.A. and Hogstrom, K.R. (2001) The Effect of Scattering Foil Parameters on Electron-Beam Monte Carlo Calculations. Medical Physics, 28, 2527-2534.
http://dx.doi.org/10.1118/1.1420387 - 16. Faj, D., Vrtar, M., Krajina, Z., Jurkovi, S. and Margareti, D. (2003) Model of Total Skin Electron Treatment Using the “Six-Dual-Field” Technique. Collegium Antropologicum, 27, 713-721.
- 17. Pavón, E.C., Sánchez-Doblado, F., Leal, A., Capote, R., Lagares, J.I., Perucha, M. and Arráns, R. (2003) Total Skin Electron Therapy Treatment Verification: Monte Carlo Simulation and Beam Characteristics of Large Nonstandard Electron Fields. Physics in Medicine and Biology, 48, 2783-2796.
http://dx.doi.org/10.1088/0031-9155/48/17/304 - 18. Precise Operators Manual (2003) Chapter 11, High Dose Rate Electron Therapy (HDRE).
- 19. Rogers, D.W.O., Walters, B. and Kawrakow, I. (2006) BEAMnrc Users Manual. National Research Council of Canada. NRCC Report, PIRS-0509(A)RevK, NRC, Ottawa.
- 20. Walters, B., Kawrakow, I. and Rogers, D.W.O. (2006) DOSXYZnrc User’s Manual. NRCC Report PIRS-794RevB, NRC, Ottawa.
- 21. Ma, C.-M. and Rogers, D.W.O. (2006) BEAMDP User’s Manual. NRCC Report PIRS-0509(C)RevA, NRC, Ottawa.
- 22. Gerbi, B.J. and Dimitroyannis, D.A. (2003) The Response of Kodak EDR2 Film in High-Energy Electron Beams. Medical Physics, 30, 2703-2705.
http://dx.doi.org/10.1118/1.1607505 - 23. Cox, R.S., Heck, R.J., Fessenden, P., Karzmark, C.J. and Rust, D.C. (1989) Development of Total Skin Electron Therapy at Two Energies. International Journal of Radiation Oncology*Biology*Physics, 18, 659-669.
http://dx.doi.org/10.1016/0360-3016(90)90075-U - 24. Turner, J.R., Hugtenburg, R.P. and Wynne, C.J. (1995) Total Skin Electron Therapy at Two Energies on a Linear Accelerator. Australasian Physical and Engineering Sciences in Medicine, 18, 208-220.
- 25. IDL, EXELIS Visual Information Solutions.
http://www.exelisvis.com
NOTES
*Corresponding author.











