Advances in Remote Sensing
Vol.2 No.3(2013), Article ID:36007,9 pages DOI:10.4236/ars.2013.23023
Study on Quantitative Model of Karst Drainage Basin Water-Holding Based on Principal Component Analysis: A Case Study of Guizhou, China*
1School of Geography and Planning, Sun Yat-sen University, Guangzhou, China
2School of Geographic and Environmental Science, Guizhou Normal University, Guizhou, China
3Department of Hydrology and Water-Recource, Guizhou Normal University, Guizhou, China
4Vocational and Technical School in Baiyun District of Guiyang City, Guizhou, China
Email: zhonghuahe@gznu.edu.cn, #eescxx@mail.sysu.edu.cn
Copyright © 2013 Zhonghua He et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 19, 2013; revised July 19, 2013; accepted August 8, 2013
Keywords: Karst Drainage Basin; Watershed Vegetation Index; Catchment Water-Holding Ability; Catchment Water-Storing Capacity; Quantitative Model
ABSTRACT
In Karst drainage basins, there are the ground water and underground water exchanging frequently, and the shortage of water resources due to having the special double aquifer mediums and unique surface and subsurface river systematic structure. This paper is to select 20 research sampling areas coming from Guizhou Province, and according to the spectral characteristics of the catchment water-holding mediums and vegetations, and using the remote sensing technique, extract the watershed vegetation index. According to the principle of principal component analysis, using the software of Spss and Matlab is to analyze the impacts of watershed vegetation type on the catchment water-holding ability, and establish the principal component analysis function. Studies have shown that: 1) the watershed vegetation coverage rate plays an important role in Karst basin water-holding ability; 2) the catchment water-holding ability is the comprehensive reflection and manifestation of the Catchment Water-storing Capacity (CWC); 3) it is much better effects and higher accuracy to monitor/forecast the catchment water-holding volume by using the vegetation indices.
1. Introduction
Karst is a kind of fragile eco-environment composed mainly of Water Resources [1]. In Karst areas, there are the surfaces broken, the slopes steep and mountains high, and the valleys deeply cut that will cause the surface water infiltrated seriously, the subsurface water deeply hidden, and the shortage of the catchment water resources. The broken Karst surfaces, shorter soil-formed times, thinner soil-layer and lower soil-fertility result in the difficulty of vegetation growth and the water/soil outflow severely. The development of the fractures and conduits within the rocky layer below surfaces causes the surface water flowing rapidly and the difficulty of catchment water-holding. Hence these will affect on the Catchment Water-storing Capacity (CWC). The catchment water-holding is the comprehensive reflection of the strong/weak of the CWC, and the manifestation of the spatial distribution of water resources. The Vegetation Index (VI) is the important information of the catchment water-holding, and through calculating and analyzing the watershed vegetation index is to reveal the catchment water-holding rules, and reflect the spatial distribution characteristic of water resources. After the developments of nearly 20 years, the Vegetation Index (VI) has dozens of kinds. It is the commonly used forms for these Vegetation Indices (VIs) like the Vegetation Index (RVI), Difference Vegetation Index (DVI), Normalized Difference Vegetation Index (NDVI), Transformational Vegetation Index (TVI), Return Difference Vegetation Index (RDVI) and Enhanced Vegetation Index (EVI). The VIs have widely applied to the studies to the global and regional land cover, vegetation classification and environmental variation [2-14]. At present, as for the studies about the Karst catchment water-holding, He zhonghua et al., [15-17] had some relevant discussions, but, the less VIs-based studying Karst catchment water-holding. This paper is to select the 20 sampling sites having the continuously 5-year observation hydrological and remote sensing data of Guizhou Province. Using the remote sensing technique extracts the watershed vegetation indices of the RVI, DVI, NDVI, TVI, RDVI and EVI from TM images. Utilizing mathematical methods explores the relationship between catchment water-holding and VIs, and establishes the quantitative remote sensing model of Karst drainage basin water-holding. At last, utilizing 5 sampling areas is to be made the significant test for the model, which has a good predictive effect. This paper is useful for the no-data regions to calculate the water resources, and provides a stronger theoretical basis for us to more fully and reasonably estimate and utilize karst water resources.
2. Sample Area Selection & Data Acquisition
2.1. Selections of the Sample Area
According to the study purpose, this paper is to select 20 sampling sites located in the central part, southern, southwest area, western and northern of Guizhou Province, respectively. They are all distributed in the typical Karst areas, with the condition of Geology and geomorphology of them similar as possible, which reflects the spatial variation characteristics and rules of catchment water-holding. Meanwhile, the 20 sample sites been in the same climatic zones is to guarantee the precipitation or watershed prophase-water content the same as possible.
2.2. Hydrologic Data
Hydrologic data comes from the Guizhou Statistics on Mean Monthly Flows per Calendar Year compiled by Guizhou Hydrologic Station and Water Resources Bulletin of Guizhou Province compiled by the Department of Guizhou Hydrology & Water Resources. This paper is to select 20 hydrologic section data that are in the same climatic zones during the period from Sep. 2005 to Sep. 2010. Drainage area is generally dominated by small watershed, which is to ensure that the geological conditions of basin underlying surfaces can be as far as possible the same or similar. To calculate the mean monthly runoff depth of 20 research sampling sites and make its standardized processing using the Formula (7) is shown on Table 4.
2.3. Remote Sensing Data
2.3.1. Preprocesses of Remote Sensing Images
(1) Selection of remote sensing data In order to guarantee less than 30% of the cloud-cover amount per research time, this paper is to select the TM images of a total of 6 periods in 6 years during the period from Sep. 2005 to Sep. 2010.
(2) Atmospheric correction Currently, there are many methods of atmospheric correction, and the atmospheric radiative transfer model is more accurate method. It is utilizing the radioactive transfer principles of electromagnetic wave in the atmosphere to be established the atmospheric correction model of remote sensing image. This paper is to adopt the FLAASH model, namely improved MORTRAN model, which can be made atmospheric correction not only for hyperspectral data, but also for multispectral data like LANDSAT, SPOT, AVHRR, MERIS, IRS and ASTER, etc.
2.3.2. Apparent Reflectance Calculation
(1) Calculation of spectral radiance
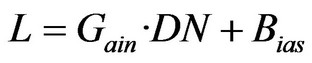 (1)
(1)
If there are no calibration parameter data of Gain and Bias, a band L can be calculated by the Formula (2)

(2)
where QCAL is the DN value of a pixel, namely QCAL=DN; QCALmax is the maximum value 255, and QCALmin is the minimum value. The Formula (2) can be changed to the Formula (3) for LandSat-7 (namely QCALmin = 1) H, and to the Formula (4) for LandSat-5 (namely QCALmin = 0).
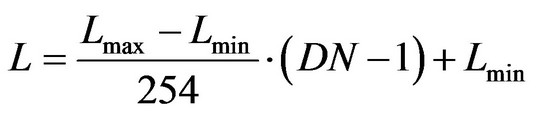 (3)
(3)
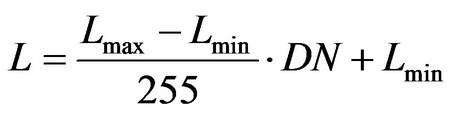 (4)
(4)
(2) Calculation of apparent reflectivity [18-20].
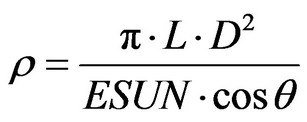 (5)
(5)
where 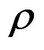 is the apparent reflectivity of the Top of the Atmosphere (TOA) (Dimensionless);
is the apparent reflectivity of the Top of the Atmosphere (TOA) (Dimensionless);  is a constant (steradian sr); D is the distance of Sun-Earth, calculated the Sun-Earth distance of any day of the year according to the Table 1; ESUN is the mean Solar spectral irradiance of the TOA, can be lookup from the Table 2 [21,22];
is a constant (steradian sr); D is the distance of Sun-Earth, calculated the Sun-Earth distance of any day of the year according to the Table 1; ESUN is the mean Solar spectral irradiance of the TOA, can be lookup from the Table 2 [21,22]; 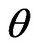 is the Solar Zenith Angle (Viz.,
is the Solar Zenith Angle (Viz., ), and
), and 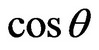 can directly calculated by the Formula (6) [23].
can directly calculated by the Formula (6) [23].
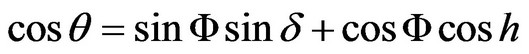 (6)
(6)
where 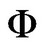 is the Geographic Latitude,
is the Geographic Latitude, 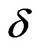 is the Solar Declination, and h is the Sun Angle
is the Solar Declination, and h is the Sun Angle
2.3.3. Selection & Calculation of Vegetation Index
From the theoretical analysis, the DN value of the originnal remote sensing image is without any correction, including the radiation calibration, is only a digital conversion form of radiant energy got into the sensor, and can’t essentially reflect the radiation characteristics of target objects. The L and 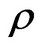 have been made radiometric calibration correction. The
have been made radiometric calibration correction. The 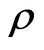 is the reflectivity of the surface features after atmospheric correction, and can essentially reflect the radiation characteristics of target objects. Therefore, the VI established by the
is the reflectivity of the surface features after atmospheric correction, and can essentially reflect the radiation characteristics of target objects. Therefore, the VI established by the 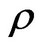 can reflect the vegetation coverage rate and its changing of watershed underlying surfaces. The common vegetation indices are listed in the following Table 3 [24-30].
can reflect the vegetation coverage rate and its changing of watershed underlying surfaces. The common vegetation indices are listed in the following Table 3 [24-30].
The Vegetation Index (VI) is a quantitative indicator of catchment water-holding, indicating that the larger (or smaller) the VI, the more (or less) the biomass and the more developed (or less developed) the plant roots, which results in the more (or less) the interception amount of vegetation to precipitation, the higher (or lower) the amount of rainfall infiltration, and shows the stronger
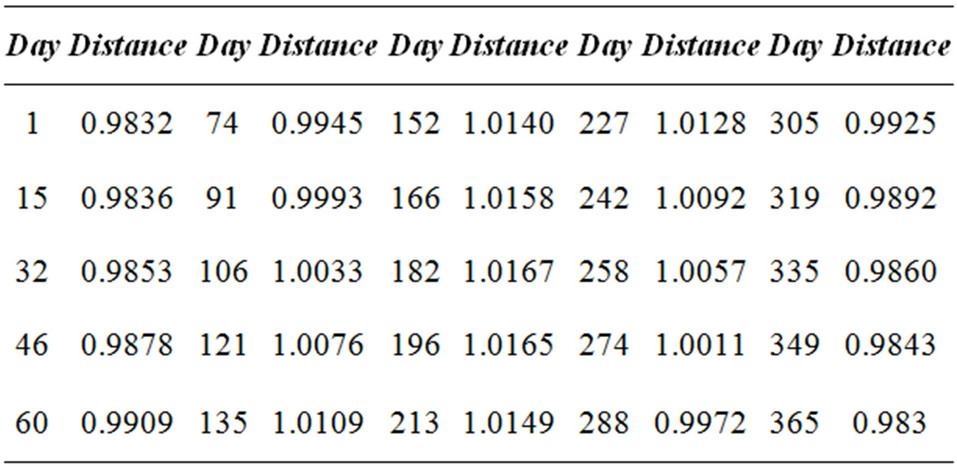
Table 1. Sun-Earth distance at different lime (Astronomical units).

Table 2. Mean solar spectral irradiance at the atmospheric top for Landsa-7 (w·m−2·μm−1).
(or weaker) the Catchment Water-storing Capacity (CWC) and the more significant (or less significant) the catchment water-holding. Therefore, the different vegetation indices are to reflect the catchment water-holding status from a different point of view. This paper is to select the remote sensing data LandSat-7, firstly, using the Formula (3) is to compute the spectral radiance of surface objects; secondly, using Formulas (5) and (6) and based on Tables 1 and 2 calculates the apparent reflectivity of them; thirdly, using the formulas of the Table 3 are to calculate the VIs of the apparent reflectivity like RVI, DVI, NDVI, TVI, RDVI and EVI and make standardized processing for them by use of the Formula (4), shown on Table 4.
3. Quantitative Analysis of Catchment Water-Holding
3.1. Principles of Quantitative Analysis
In Karst drainage basins, there are many factors affecting on catchment water-holding ability, and which are complex and changeable relationships. In this study, taking vegetation factors as an example is to explore the impacts of vegetation factors under different level (or factor) on catchment water-holding ability. Utilizing the principle of principal component analysis is to compute the contribution rate of each factor of vegetations to catchment water-holding [31,32].
1) The original data matrix X
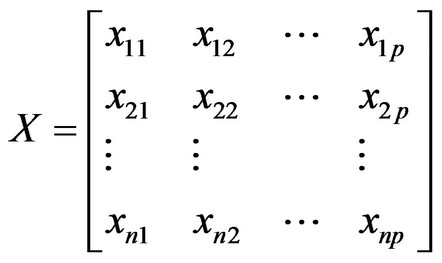
And make standardized processing, Viz.,
 (7)
(7)
where p is the number of variables; n is the number of

Table 3. The VI formulas in this paper.
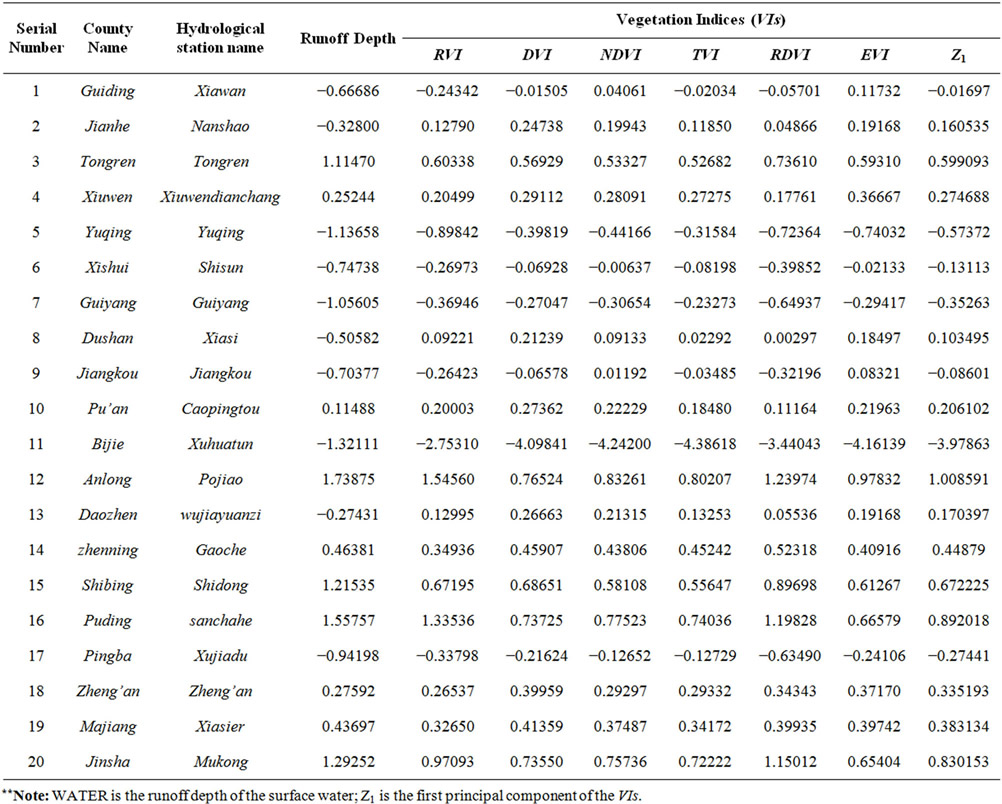
Table 4. The hydrological data and VIs of Karst basin sample areas.
samples;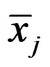 ,
, 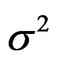 is the sample mean and total variance, respectively. Its expression is as follows:
is the sample mean and total variance, respectively. Its expression is as follows:
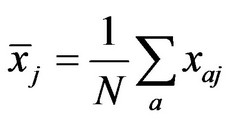
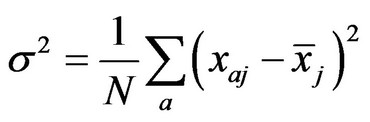
2) Calculate the correlation coefficient matrix R
 (8)
(8)
where r is the correlation coefficient; N is the total number of samples.
3) Calculation of eigenvalues and eigenvectors According to the characteristic equation 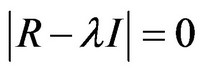 is to calculate the eigenvalue, Viz., solving the characteristic polynomial:
is to calculate the eigenvalue, Viz., solving the characteristic polynomial:
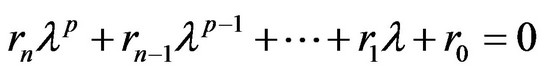 (9)
(9)
To compute the value of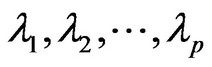 , and sorted
, and sorted 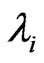 by size as the following:
by size as the following:
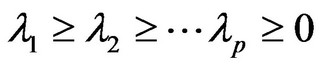
The eigenvector (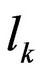 ) of the eigenvalue (
) of the eigenvalue (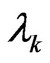 ) is listed by
) is listed by
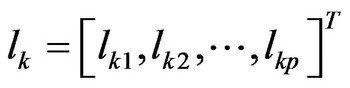
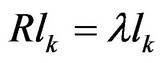 (10)
(10)
4) To calculate the contribution ratio 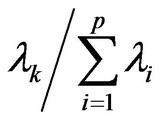 and the cumulative contribution ratio
and the cumulative contribution ratio
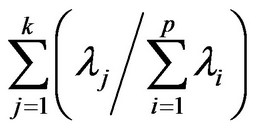 (11)
(11)
To take generally the principal component of the eigenvalue 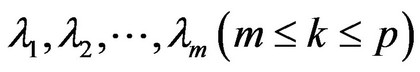 of greater than 80% of cumulative contribution ratio.
of greater than 80% of cumulative contribution ratio.
5) Calculation of Principal component loading
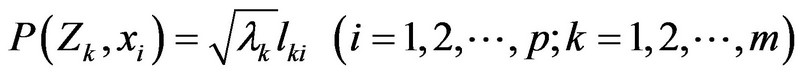 (12)
(12)
6) Calculation of principal component scores according to the Formula (13)
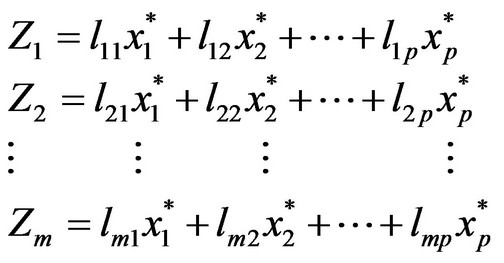 (13)
(13)
Principal component score matrix is as follows
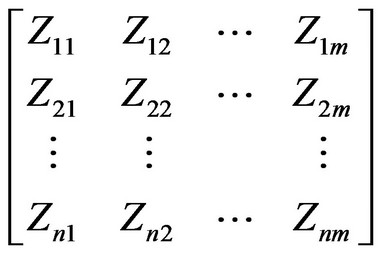
where Z1, Z2,…, Zm is the first principal component, the second principal component, …, and the m principal component, respectively.
3.2. Calculation & Analysis of Principal Components
On basis of the Table 4, using the statistical software of Spss and Matlab, and the Formulas (8)-(13) is to firstly calculate the relationship between different VIs and runoff depth (Table 5), secondly, compute the total variance of the factors (Table 6), rotated component matrix and component score coefficient matrix (Table 7).
(1) Table 5 shows that the correlation coefficients (R) between all the vegetation indices and runoff depth are greater than 0.5, indicating that the roles of vegetation coverage rate to catchment water-holding in Karst drainage basins should not be underestimated. Namely the impact of the VIs on runoff depth is very great, and the maximum is the Ratio Vegetation Index (RRVI = 0.847) and Return Difference Vegetation Index (RRDVI = 0.82), followed by the Enhanced Vegetation Index (REVI = 0.629) and Difference Vegetation Index (RDVI = 0.621), and the minimum is the Normalized Difference Vegetation Index (RNDVI = 0.613) and Transformational Vegetation Index (RTVI = 0.601).Meanwhile it shows that the impact degree of different vegetation indices on runoff depth is different.
(2) Table 6 also shows that: in the description of the initial factor solution, the eigenvalue of the first factor is 6.141, which explains the 97.136% of total variance of six original factors and 97.36% of cumulative variance contribution ratio; and the eigenvalue of the second factor is 0.156, which explains the 2.461% of total variance of six original factors and 99.597% of cumulative variance contribution ratio. In the solution condition of total variance after extracting factors, Table 6 demonstrates that one factor is extracted after extracting factors by using principal component method, and one factor explains the 97.136% of total variance of six original factors and 2.864% of information loss amount, and the results were better explained.
(3) Table 7 represents the rotated factor loading matrix, namely principal component is relevance with six factors. From the Table 7, the correlation coefficient between the First Principal Component (FPC) and the six original factors is greater than 0.9, indicating that the FPC is loaded more than 90% of the information of the six original factors, and achieves the purpose of reducing a number of variables.
(4) Table 7 is the Factor Score Coefficient Matrix (FSCM). The FSCM estimated by regression analysis
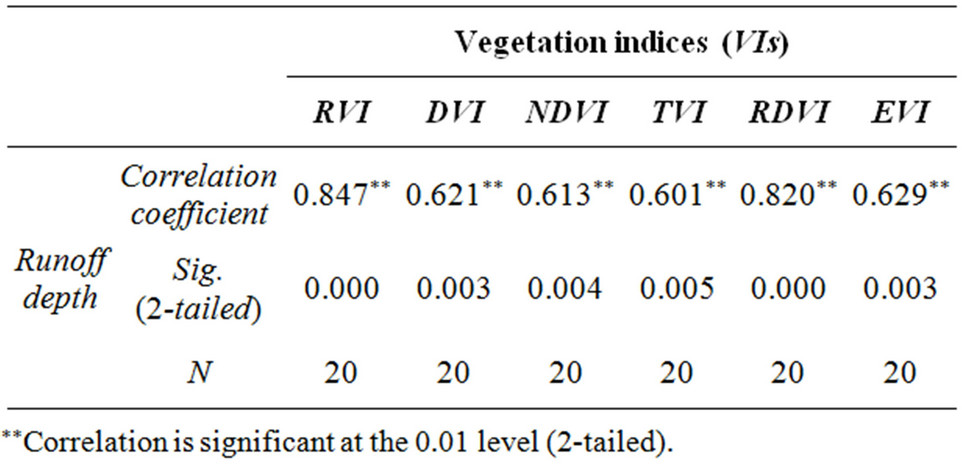
Table 5. The correlation coefficient between the VIs and the runoff depth.
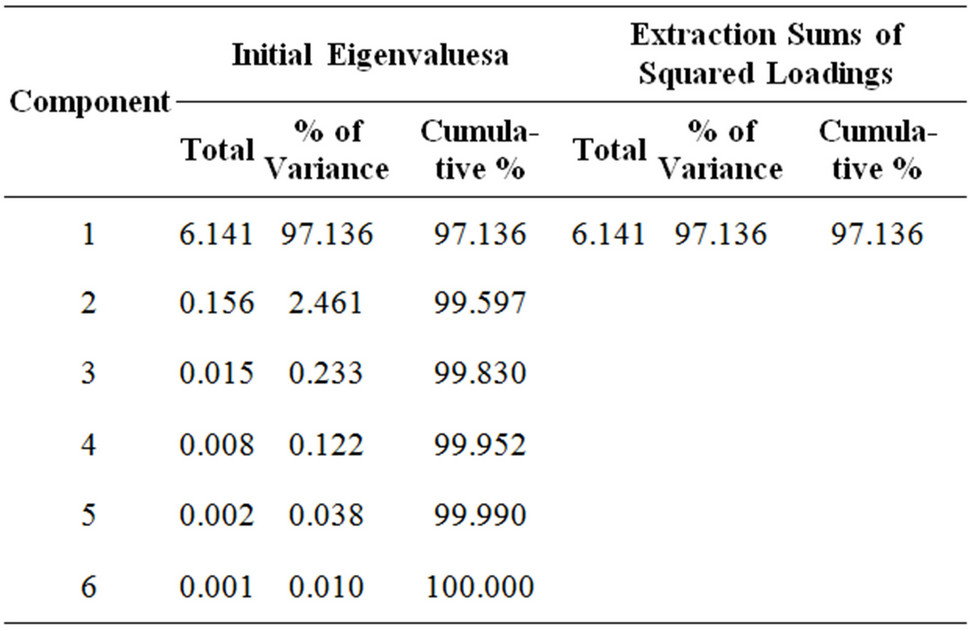
Table 6. Total variance of factors explained.

Table 7. The rotated component loading matrix and component score coefficient matrix.
expresses the score of six factors like RVI, DVI, …, EVI. The Z1 is represented the FPC, then, the Table 7 may be written as the score function
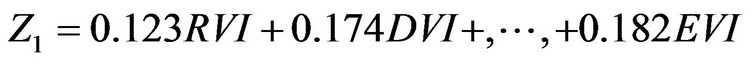 (14)
(14)
4. Quantitative Model Establishment of Catchment Water-Holding
4.1. Principle of Quantitative Model
Suppose that the relationship between hydrologic sectional observation value y and vegetation indices x in Karst drainage basins can be expressed by the following model [31,32].
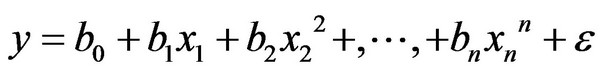 (15)
(15)
where b0 is the constant, and b1, b2, bn is the coefficient of independent variables x1, x2, xn, respectively; 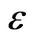 is the random variable obeyed normal distribution with the mean 0 and variance
is the random variable obeyed normal distribution with the mean 0 and variance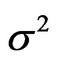 . In order to evaluate the precision of regression equation that needs to be made significant test with the statistic F.
. In order to evaluate the precision of regression equation that needs to be made significant test with the statistic F.
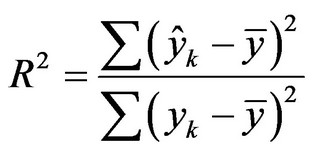 (16)
(16)
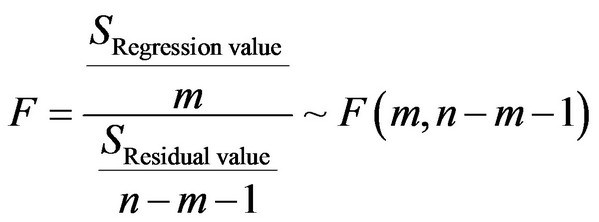 (17)
(17)
where SRegression value is the regression value, and is equal to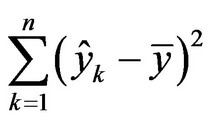 ; RResidual value is the residual value, and is equal to
; RResidual value is the residual value, and is equal to .
.
The statistic F is obeyed the F-distribution with the first freedom degree m and second freedom degree n-m-1. The critical value Fα(m, n-m-1) can be lookup from F-distribution table with a given α (such as α = 0.05).If the statistic value F is greater than critical value Fα(m, n-m-1), indicating that the regression model established with these data is significant and can be used for the analysis of regional water resources, In contrast, can not be used.
4.2. Establishment of Quantitative Model
Firstly, on basis of Table 4, using the Formula (14) is to calculate the FPC (z1) of the VIs of six factors, and shown on the Table 4. Secondly, on basis of the Table 4 again, using the Formula (15) and the Spss and Matlab Software is to compute the quantitative model coefficient between catchment water-holding and FPC (Z1) of the VIs, and shown on the Table 8. Thirdly, the model-fitted degree between catchment water-holding and FPC (Z1) is computed utilizing the Formula (16) and made significant test with the F-distribution by the Formula (17) (Table 8).
(1) We know from the Table 8 that the catchment water-holding (WATER) of Karst drainage basins is fitted by the FPC (Z1) of the VIs, with very good its fitting effect and very high the model-fitted coefficient (R = 0.974). The dynamic change model of catchment water-holding is established by using the Formula (15), with very high the multiple correlation coefficient (R2 = 0.974) and very small the root mean square error (RMSE = 0.1513). The quantitative model established by using the Formula (17) is to be made the F-test. The statistic value (F = 313.732) is greater than the critical value (F0.01 = 6.11), indicating that the built quantitative model is significant, and illustrating that it is very good to monitor dynamically the catchment water-holding with the first principal component of vegetation index.
(2) On basis of the Table 8 and using the Formula (15), the dynamic change monitoring, forecasting quantitative model of Karst drainage basin water-holding can be expressed as the following:
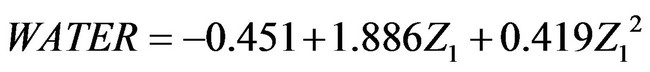 (18)
(18)
To sum up, in Karst areas, there are the hydrology dynamic changes violently, surface water infiltrated severely and the catchment water-holding ability badly due mainly to the rugged surface, caves and conduits crisscrossed subsurface; the thinner soil-layer and lower soilfertility result in the difficulty of vegetation growth, and the water/soil outflow severely; which is to be formed a special, fragile karst environment, and restricts severely the Catchment Water-storing Capacity (CWC). The catchment water-holding is the manifestation of the CWC, while the VI is the important information of the catchment water-holding and an important indicator of the CWC. A large/small of the VIs is to affect on the velocity and residence time of rainfall in the catchment surface and the rainfall infiltration amount, which further influences the large/small of the CWC. Therefore, the vegetation index is the comprehensive reflection and manifestation of the catchment water-storing and water-holding.
4.3. Evaluation of the Model Accuracy
In order to assess the accuracy of the monitoring, forecasting quantitative model, the 5 research sampling areas selected randomly in Karst drainage basin, made some processing using the above methods, are to be extracted the VIs, respectively, e.g., RVI, DVI, NDVI, TVI, RDVI and EVI. Utilizing the Formula (14) is to calculate the FPC (z1) value (Table 9). The Table 9 is computed by using the Formula (18) and Eviews software, and the

Table 8. The coefficient table of models.
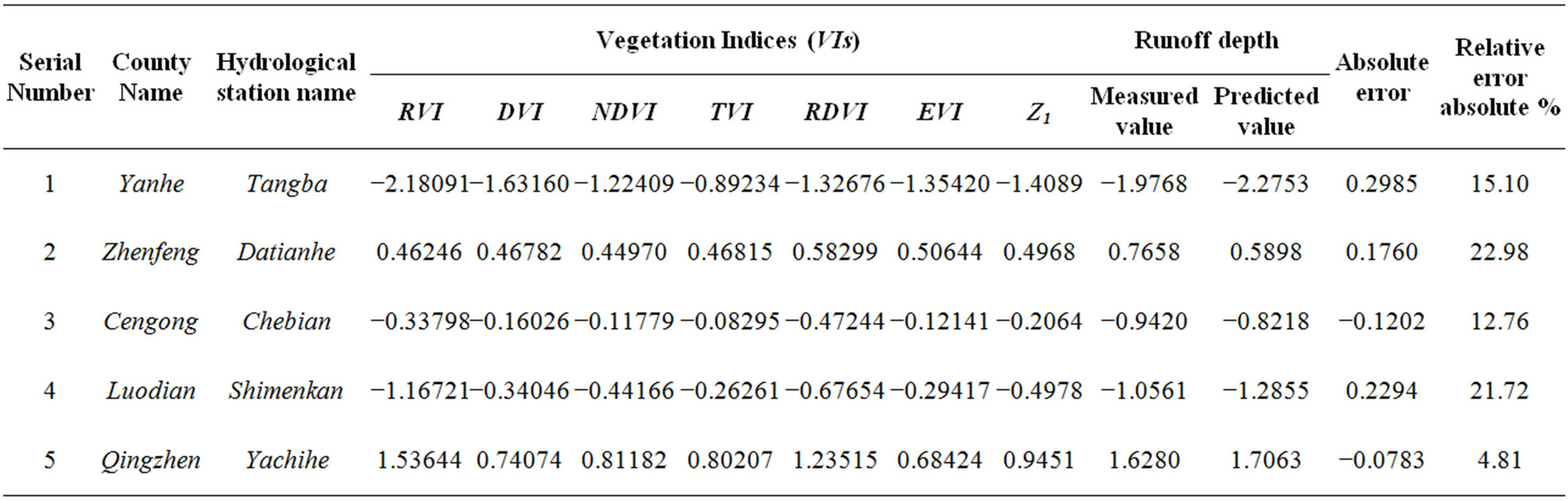
Table 9. The model-test table.
results are compared with the runoff depth measured value, which concluded the 22.98% of the maximum relative error value, 4.81% of the minimum relative error value. It indicates that the FPC of the VIs can be used to dynamically monitor, forecast the catchment waterholding, with very good the effect and very high the accuracy.
5. Conclusions and Analysis
(1) The correlation coefficient between the VIs and the runoff depth is greater than 0.5, indicating that the vegetation coverage rate in Karst drainage basins plays an important role in the catchment water-holding. The descending order of the impacts of the different vegetation indices on the catchment water-holding is the RVI (0.847) > RDVI (0.82) > EVI (0.629) > DVI (0.621) > NDVI (0.613) > TVI (0.601).
(2) The first principal component function model based on the VIs can be expressed as the following:
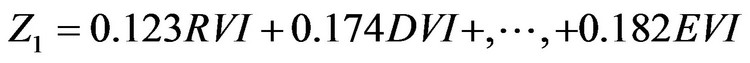
(3) The dynamic monitoring, forecasting quantitative model of catchment water-holding based on the FPC can also be expressed as the following:
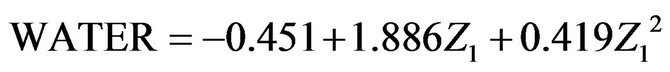
This model through the variance analyzing and the sample areas testing shows very good monitoring, prediction effect.
In short, in Karst areas, there are the mountains high and slopes steep, carbonate rocks distributed widely, and the surface and subsurface connected, interlinked everywhere, which causes the surface and subsurface water exchanging frequently, the catchment water-holding difficultly. The watershed vegetation index is the important information of the catchment water-holding situation and its spatial distribution. The catchment water-holding model based on the FPC of the VIs, on the one hand, reflects the catchment water-holding situation from the different angles of the VIs; on the other hand, extracting the principal component will reach to reduce the number of variables and the relevance between the variables, make that the model can comprehensively reflect the catchment water-holding situation and its spatial distribution characteristics, and the model prediction accuracy is higher. Establishing the Karst drainage basin water-holding model based on the FPC of the VIs, is to be applied to solving the calculations of the water resources volume in no-data areas, and provides a strong theoretical basis for us to more fully estimate, more rationally utilize the Karst water resources.
REFERENCES
- M. D. Yang, “Karst Basin Hydrogeomorphic System,” Geological Publishing, Beijing, 1998.
- Z. G. Tang, J. H. Ma, C. L. Li, et al., “Estimating Vegetation Coverage Using Remote Sensing Data in Sanjiangyuan National Nature Reserve,” Journal of Lanzhou University (Natural Sciences), Vol. 46, No. 2, 2010, pp. 11-16.
- L. P. Yi, L. K. Yin and L. T. Wang, “Study on Dynamic Change of Yuli Oasis Plant Cover Based on RDVI,” Journal of Arid Land Resources & Environment, Vol. 18, No. 6, 2004, pp. 66-71.
- Y. L. Liu, Y. H. Ren, T. Chen, et al., “Comparisions of Estimating Methods of Vegetation Fraction Based on ‘BJ-1’ Microsatellite Imagery,” Remote Sensing Technology and Application, Vol. 22, No. 5, 2007, pp. 581- 585.
- X. Yao, Y. Zhu, W. Feng, et al., “Exploring Novel Hyperspectral Band and Key Index for Leaf Nitrogen Accumulation in Wheat,” Spectroscopy and Spectral Analysis, Vol. 29, No. 8, 2009, pp. 2191-2195.
- Q. W. Zeng, H. G. Wu and M. Su, “Study on Remote Sensed Monitoring of Forest Canopy Change Based on TM Data,” Remote Sensing Technology and Application, Vol. 24, No. 2, 2009, pp. 186-191.
- D. W. Wang, C. Y. Huang, Q. J. Ma, et al., “Quantitative Model of Aboveground Dry Matter Accumulation from Different Components of Cotton Using Hyperspectral Data,” Journal of Shihezi University (Natural Science), Vol. 25, No. 5, 2007, pp. 529-533.
- L. H. He, K. H. Chu and X. M. Xiao “The Relationship of Vegetaion-Derived Index and Site-Measured Rice LAI,” Journal of Remote Sensing, Vol. 8, No. 6, 2004, pp. 672- 676.
- F. M. Wang, J. F. Huang, Y. L. Tang, et al., “Estimation of rice LAI by using NDVI at different spectral bandwidths,” Chinese Journal of Applied Ecology, Vol. 18, No. 11, 2007, pp. 2444-2450.
- X. Yang, J. J. Wu, F. Yan and J. Zhang, “Assessment of Regional Soil Moisture Status Based on Characteristics of Surface Temperature/Vegetation Index Space,” Acta Ecologica Sinica, Vol. 29, No. 3, 2009, pp. 1205-1216.
- Y. X. Li, W. N. Yang, L. Tong, et al., “Remote Sensing Quantitative Monitoring and Analysis of Fuel Moisture Content Based on Spectral Index,” Acta Optica Sinica, Vol. 29, No. 5, 2009, pp. 1403-1407. doi:10.3788/AOS20092905.1403
- A. Karnieli, N. Agam, et al., “Use of NDVI and Land Surface Temperature for Drought Assessment,” Journal of Climate, Vol. 23, No. 3, 2010, pp. 618-633. doi:10.1175/2009JCLI2900.1
- R. L. Pu, P. Gong, Y. Tian, et al., “Using Classification and NDVI Differencing Methods for Monitoring Sparse Vegetation Coverage: A Case Study of Saltcedar in Nevada, USA. International Journal of Remote Sensing, Vol. 29, No. 14, 2008, pp. 3987-4011. doi:10.1080/01431160801908095
- P. S. Thenkabail, “Inter-sensor Relationships between IKONOS and Landsat-7 ETM+ NDVI Data in Three Ecoregions of Africa,” International Journal of Remote Sensing, Vol. 25, No. 2, 2004, pp. 389-408. doi:10.1080/0143116031000114842
- Z. H. He, H. Liang, S. T. Yang, et al., “The Identification of the Drainage Basin Low-Flow Resources on RS,” Journal of Guizhou Normal University (Natural Science), Vol. 22, No. 2, 2004, pp. 36-39.
- Z. H. He, S. T. Yang, H. Liang, et al., “Identification for the Factors That Impact Low-Flow Resources in Karst Basin by Means of GIS and RS-A Case in Guizhou Province,” Carsologica Sinica, Vol. 23, No. 1, 2004, pp. 48- 55.
- Z. H. He, H. Liang, Huang F.S., et al., “The influencing factor analysis of geomorphologic development of karst drainage based on DEM,” Science of Surveying and Mapping, Vol. 33, No. 4, 2008, pp. 70-72
- B. L. Markham and J. L. Barker, “Thematic Mapper Bandpass Solar Exoatmospheric Irradianees,” International Journal of Remote Sensing, Vol. 8, 1987, pp. 513- 523.doi:10.1080/01431168708948658
- M. Roderick, R. Smith and G. Lodwick, “Calibrating Long-Term AVHRR-Derived NDVI Imagery,” Remote Sensing of Environment, Vol. 58, No. 1, 1996, pp. 1-12. doi:10.1016/0034-4257(96)00035-1
- Huete A, et al. “Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sensing of Environmen, Vol. 83, No. 1, 2002, pp. 195-213. doi:10.1016/S0034-4257(02)00096-2
- G. Chander and B. Markham, “Revised Landsat-5 TM Radiometric Calibration Procedures and Post-Calibration Dynamic Ranges,” 2003. http://landsat.usgs.gov/documents/L5TMCal2003.pdf.
- G. Chander and B. Markham, “Revised Landsat-5 TM radiometric ranges,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 41, No. 11, 2003. http://landsat.usgs.gov/cpf/cpf_notes15.html.
- S. H. Lv, “Physical Foundation of Remote Sensing,” Commercial Press, Beijing, 1981, pp. 206-234.
- C. F. Jordan, “Derivation of Leaf Area Index from Quality of Light on the Forest Floor,” Ecology, Vol. 50, No. 4, 1969, pp. 663-666. doi:10.2307/1936256
- R. L. Pearson and D. L. Miller, “Remote Mapping of Standing Crop Biomass for Estimation of the Productivity of the Short-Grass Prairie,” Proceedings of the Eighth International Symposium on Remote Sensing of Environment, Vol. 2, 1972, pp. 1357-1381
- J. W. Rouse, R. H. Haas, J. A. Schell, D. W. Deering and J. C. Harlan, “Monitoring the Vernal Advancement of Retrogradation of Natural Vegetation,” NASA/GSFC, Final Report, Greenbelt, 1974.
- A. J. Richardson and C. L. Wiegand, “Distinguishing Vegetation from Soil Background Information,” Photogrammetric Engineering and Remote Sensing, Vol. 43, 1977, pp. 1541-1552.
- A. R. Huete, “A Soil-Adjusted Vegetation Index (SAVI),” Remote Sensing of Environment, Vol. 25, No. 3, 1988, pp. 295-309. doi:10.1016/0034-4257(88)90106-X
- F. Baret, G. Guyot and D. J. Major, “TSAVI: A Vegetation Index Which Minimizes Soil Brightness Effects on LAI and APAR Estimation,” Proceedings of 12th Canadian Symposium on Remote Sensing, Vol. 3, 1989, pp. 1355-1358.
- J. L. Reujean and F. M. Breon, “Estimating PAR Absorbed by Vegetation from Bidirectional Reflectance Measurements,” Remote Sensing of Environment, Vol. 51, No. 3, 1995, pp. 375-384. doi:10.1016/0034-4257(94)00114-3
- S. Zhang and B.-G. Yang, “The Basis of Quantitative Geography,” Higher Education Press, Beijing, 1985.
- J. H. Stock and M. W. Watson, “Introduction to Econometrics,” 2nd Edition, Shanghai People’s Publishing Press, Shanghai, 2007.
NOTES
*This study was jointed funded by Natural Science Funds from Department of Water Resources of Guizhou Province, China ((KT 201105), (KT 201010), (KT200802)), and Guizhou Science and Technology Department (QKHJ (2010)2026), (QKHJ (2013)2208), and Department of Education of Guizhou Province (QJK 2009 (0039) and QJK-2006307).
#Corresponding author.

