Advances in Nanoparticles
Vol.05 No.04(2016), Article ID:70412,12 pages
10.4236/anp.2016.54020
Simulation of Natural Convection Heat Transfer Enhancement by Nanoparticles in an Open-Enclosure Using Lattice Boltzmann Method
Mohammad Mehdi Keshtkar
Department of Mechanical Engineering, Kerman Branch, Islamic Azad University, Kerman, Iran

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 20, 2014; Accepted: September 4, 2016; Published: September 7, 2016
ABSTRACT
A numerical analysis is performed to investigate the laminar, free convection flow in an Open Enclosure Using Lattice Boltzmann Method (LBM) in the presence of Carbon nanotube and Cu nanoparticles. The problem is studied for different volume fractions of nanoparticles, and aspect ratio of the cavity for various Rayligh numbers. The volume fraction of added nanoparticles to water (as base fluid) is lower than 1% to make dilute suspensions. The study presents a numerical treatment based on LBM to model convection heat transfer of Carbon nanotube based nanofluids. Results show that adding a low value of Carbon nanotube to the base fluid led to significant enhancement of convection rate. Results show that adding nanoparticles to the base fluid enhances the rate of natural convection in a cavity. Make a comparison between Carbon nanotube and Cu-nanoparticles shows that the Carbon nanotube-nano- particle has better performance to enhance convection rate at comparison with Cu- nanoparticles.
Keywords:
Lattice Boltzmann Method, Carbon Nanotube, Effective Thermal Conductivity, Effective Viscosity, Natural Convection

1. Introduction
The enhancement of fluids heat transfer is an interesting topic for different kinds of industrial and engineering applications. A well-known way to enhance the rate of convection heat transfer of conventional fluids such as water, oil and ethylene glycol which has low thermal conductivity [1] [2] is adding nano scale conductive particles. The added particles can be metals [3] , non metals [4] or Carbon nanotubes [5] [6] . Because of the high thermal conductivity of these particles, they can improve conductivity of the suspensions systematically. Nowadays, nanoparticle added fluids are known as nanofluid that first time Choi [7] named this kind of fluid suspensions. He presented enhancement of convection heat transfer by adding nanoparticles to the fluids. In recent years, many studies have been conducted to study heat transfer of nanofluids numerically and experimentally [7] - [12] . Khanafer et al. [8] presented a heat transfer enhancement by adding nanoparticles to fluid in a two dimensional enclosures at natural convection regime for the different Grashof numbers. They presented an increase of 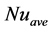 about 7.5%, 12%, 15.5% and 20%, respectively, by adding a volume fraction of added Cu nanoparticles to the Water equal to 4%, 6%, 8% and 10% when
about 7.5%, 12%, 15.5% and 20%, respectively, by adding a volume fraction of added Cu nanoparticles to the Water equal to 4%, 6%, 8% and 10% when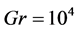 . Gherasim et al. [9] conducted to an experimental study and represented heat transfer enhancement possibility of coolants with suspended Al2O3 nanoparticles dispersed in water inside a radial flow cooling device. Saleh et al. [10] studied convection heat transfer of a nanofluid-filled trapezoidal enclosure. They investigated the effect of different volume fraction of Al2O3 and Cu nanoparticles on heat transfer enhancement of Water as base fluid. They reported an enhancement of natural convection heat transfer about 2.4%, 4.7%, 7.1%, 9.5% and 11.9% by adding a
. Gherasim et al. [9] conducted to an experimental study and represented heat transfer enhancement possibility of coolants with suspended Al2O3 nanoparticles dispersed in water inside a radial flow cooling device. Saleh et al. [10] studied convection heat transfer of a nanofluid-filled trapezoidal enclosure. They investigated the effect of different volume fraction of Al2O3 and Cu nanoparticles on heat transfer enhancement of Water as base fluid. They reported an enhancement of natural convection heat transfer about 2.4%, 4.7%, 7.1%, 9.5% and 11.9% by adding a 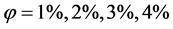 and 5% of Al2O3 nanoparticles when the angle of side walls are 23.96˚ at
and 5% of Al2O3 nanoparticles when the angle of side walls are 23.96˚ at 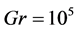 and also for Cu nanoparticles at same condition the values are about 3.9%, 7.9%, 11.8%, 15.7%, 19.5%. In 1991, Iijima [13] discovered Carbon nanotubes as an allotrope of Carbon which is made of long-chained molecules of Carbon with Carbon atoms arranged in a hexagonal complex to form a tubular structure. In last decade Carbon nanotubes has been mentioned as attractive topic by many researches which is generally due to their special properties at physical view such mechanical and thermal properties. At this point of view, the Carbon nanotubes have extraordinary thermal properties such as thermal conductivity about twice as high as diamond [14] or thermal stability up to 2800 C in vacuum. The higher thermal conductivity of Carbon nanotubes relative to other nanoparticles led to that the nanofluids containing cylindrical Carbon nanotubes are expected to have better heat transfer properties compared with the other nanofluids with spherical nanoparticles [15] [16] . Gavili et al. [17] simulated the mixed convection in a two-sided lid-driven differentially heated square cavity for nanofluids containing Carbon nanotubes for nanofluids. Natural convection in a square cavity and its fluid flow is a classical benchmark in heat transfer problems. Open cavities are a kind of 2-D cavity which has an open side. These kinds of cavities have special physics for both flow and temperature fields in open side because of outgoing of flow from this side. Many studies have been done on analysis of buoyant flows and their heat transfer in open cavities. Javam et al. [18] investigated stability of stratified natural convection flow in open cavities. Mohammad et al. [19] presented natural convection in an open ended cavity and slots they analyzed the effect of aspect ratio of cavity on heat transfer rate. They also presented a good procedure for simulating open boundaries in Lattice Boltzmann Method, their technique demonstrated the abilities of the LBM to simulate Natural convection in open cavities. The progress of using the Lattice Boltzmann Method (LBM) as a numerical technique to simulate the heat transfer and fluid flow has been
and also for Cu nanoparticles at same condition the values are about 3.9%, 7.9%, 11.8%, 15.7%, 19.5%. In 1991, Iijima [13] discovered Carbon nanotubes as an allotrope of Carbon which is made of long-chained molecules of Carbon with Carbon atoms arranged in a hexagonal complex to form a tubular structure. In last decade Carbon nanotubes has been mentioned as attractive topic by many researches which is generally due to their special properties at physical view such mechanical and thermal properties. At this point of view, the Carbon nanotubes have extraordinary thermal properties such as thermal conductivity about twice as high as diamond [14] or thermal stability up to 2800 C in vacuum. The higher thermal conductivity of Carbon nanotubes relative to other nanoparticles led to that the nanofluids containing cylindrical Carbon nanotubes are expected to have better heat transfer properties compared with the other nanofluids with spherical nanoparticles [15] [16] . Gavili et al. [17] simulated the mixed convection in a two-sided lid-driven differentially heated square cavity for nanofluids containing Carbon nanotubes for nanofluids. Natural convection in a square cavity and its fluid flow is a classical benchmark in heat transfer problems. Open cavities are a kind of 2-D cavity which has an open side. These kinds of cavities have special physics for both flow and temperature fields in open side because of outgoing of flow from this side. Many studies have been done on analysis of buoyant flows and their heat transfer in open cavities. Javam et al. [18] investigated stability of stratified natural convection flow in open cavities. Mohammad et al. [19] presented natural convection in an open ended cavity and slots they analyzed the effect of aspect ratio of cavity on heat transfer rate. They also presented a good procedure for simulating open boundaries in Lattice Boltzmann Method, their technique demonstrated the abilities of the LBM to simulate Natural convection in open cavities. The progress of using the Lattice Boltzmann Method (LBM) as a numerical technique to simulate the heat transfer and fluid flow has been
obvious in the last decade [20] - [23] . The Lattice Boltzmann Method has well-known advantages such easy implementation, possibility of parallel coding and simulating of complex geometries and fluid dynamic problems such as melting, fuel cell, porous media, nanofluids and etc. The convection heat transfer of different nanoparticle-based nanofluid in a cavity was mentioned in current years [24] - [27] . Fattahi et al. [24] applied Lattice Boltzmann Method to study natural convection heat transfer of Al2O3 and Cu nanofluid in a cavity. Their results show that increasing the solid volume fraction led to a heat transfer enhancement at any Rayleigh number and also heat transfer increases with increase in Rayleigh number for a particular volume fraction. Nemati et al. [25] applied LBM to investigate the effect of Cu, Al2O3 and CuO nanoparticles on mixed convection in a lid-driven cavity. Their results show that adding nanoparticles increase the rate of mixed convection heat transfer of the base fluid for all tested Reynolds numbers. Abu-Nada and Chamkha [26] conducted to study of mixed convection heat transfer of Water-Al2O3 nanofluid in an inclined cavity. Heat transfer enhancement due to increase of nanoparticles volume fraction at different Richardson and Grashof numbers was presented in their results. Their results show that 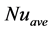 on hot wall enhances about 3.3%, 8.4%, 11.9% and 17.2% respectively for
on hot wall enhances about 3.3%, 8.4%, 11.9% and 17.2% respectively for 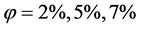 and 10% at
and 10% at  and
and 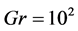 when the inclination angle of the cavity is equal to zero and also this values are 3%, 8.5%, 12% and 17% for
when the inclination angle of the cavity is equal to zero and also this values are 3%, 8.5%, 12% and 17% for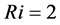 . The investigation of the heat transfer enhancement by adding the Carbon nanotube to the base fluid in an open-ended cavity is the main aim of the present study. Also a comparison between one type of Carbon nanotubes i.e. single wall Carbon nanotubes (SWCNT) and Cu-nano- particles is one of the major tasks of the study. In this simulation the effective conductivity and viscosity were calculated based on the new theoretical models. The presented model by Masoumi et al. [28] is applied for effective viscosity of the Cu and Carbon nanotube-nanofluid. To simulate thermal conductivity of Carbon nanotube-nanofluid a new theoretical model presented by Sabbaghzadeh and Ebrahimi [29] is used. On other hand, the study applies the Patel model [30] to evaluate of the effective thermal conductivity of Cu-nanofluid. To the best of author knowledge, the effects of carbon nanotubes on flow and thermal fields of natural convection is an unknown perspective which is not understand heretofore. Therefore, in this study the used numerical method is LBM with coupled double population approach for flow and temperature fields. The effect of the volume fraction of the Cu and Carbon nanotube-particles on average Nusselt number, streamlines and temperature contours is investigated for various Rayligh numbers. Also the aspect ratio of the cavity is studied as an important geometric parameter of the 2D cavities in different condition to exhibit the role of this parameter on both heat transfer rate and fluid flow of the base fluid and the nanofluid.
. The investigation of the heat transfer enhancement by adding the Carbon nanotube to the base fluid in an open-ended cavity is the main aim of the present study. Also a comparison between one type of Carbon nanotubes i.e. single wall Carbon nanotubes (SWCNT) and Cu-nano- particles is one of the major tasks of the study. In this simulation the effective conductivity and viscosity were calculated based on the new theoretical models. The presented model by Masoumi et al. [28] is applied for effective viscosity of the Cu and Carbon nanotube-nanofluid. To simulate thermal conductivity of Carbon nanotube-nanofluid a new theoretical model presented by Sabbaghzadeh and Ebrahimi [29] is used. On other hand, the study applies the Patel model [30] to evaluate of the effective thermal conductivity of Cu-nanofluid. To the best of author knowledge, the effects of carbon nanotubes on flow and thermal fields of natural convection is an unknown perspective which is not understand heretofore. Therefore, in this study the used numerical method is LBM with coupled double population approach for flow and temperature fields. The effect of the volume fraction of the Cu and Carbon nanotube-particles on average Nusselt number, streamlines and temperature contours is investigated for various Rayligh numbers. Also the aspect ratio of the cavity is studied as an important geometric parameter of the 2D cavities in different condition to exhibit the role of this parameter on both heat transfer rate and fluid flow of the base fluid and the nanofluid.
2. Lattice Boltzmann Method for Flow and Thermal Fields
The LBM utilizes two distribution functions, for the flow and temperature fields. It uses modeling of movement of fluid particles to define macroscopic parameters of fluid flow. The distribution functions are obtained by solving the lattice Boltzmann Equation (LBE), which is a special form of the Kinetic Boltzmann Equation.
The basic form of the Lattice Boltzmann Equation with an external force by introducing BGK approximations can be written as follows for the both flow and the temperature fields [20] :
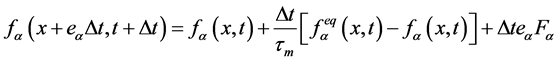 (1)
(1)
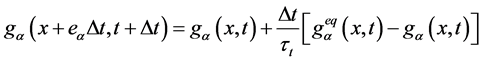 (2)
(2)
 and
and  are the dimensionless collision-relaxation times for the flow and temperature fields, respectively. They defined as follows [31] :
are the dimensionless collision-relaxation times for the flow and temperature fields, respectively. They defined as follows [31] :
 (3)
(3)
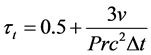
By considering D2Q9 model as shown in Figure 1, for applied lattice scheme for both flow and temperature fields, equilibrium distribution functions for flow field (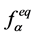 ) and temperature field (
) and temperature field (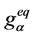 ) are calculated as follows in different
) are calculated as follows in different 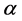 directions:
directions:


For these model the values of 


Figure 1. Discrete velocity vectors for the D2Q9 model of LBM.


In order to incorporate external force in collision part of Lattice Boltzmann model (Equation (1)), radiation heat transfer and viscous dissipation are neglected at the numerical simulation. Therefore, to capture buoyancy force effects in the flow field, the Boussinesq approximation is applied. Thus, to model buoyancy force in Equation (1), the external force needs to be assumed as below in the needed direction:

Finally, macroscopic variables can be calculated as follows:
Flow density:


3. Nanofluids Modeling
At present study, nanofluid is assumed as a single phase fluid. Thermal diffusivity of nanofluid is as follows:

The density, heat capacitance and thermal expansion of nanofluid can be defined as [32] :



The effects of nanoparticles on the viscosity of nanofluids are introduced by the so- called apparent viscosity which is presented by 

4. Main Problem
In the present study, the effects of Carbon nanotube and Cu-nanoparticles on natural convection heat transfer in a 2D deep open cavity are investigated using the Lattice Boltzmann Method based on double population approach and bounce back method. The horizontal walls of the cavity are assumed to be insulated while the left wall is maintained at a uniform temperature (

Figure 2. Schematic geometry of the problem.
gated for different Rayligh numbers at the range of 
The dimensionless quantities are as follows:

The boundary conditions on the solid walls are in the following forms:

The boundary conditions on the east open side (

The boundary conditions in the LBM can be implemented through the distribution function. For both flow and thermal fields, the distribution functions out of the domain
Table 1. Thermo-physical properties of the base fluid and nanoparticles [17] [30] .
are known from the streaming process. The unknown distribution functions are those toward the domain.
5. Result and Discussion
The presence of nanotube particles with high thermal conductivity in suspensions has different effects on temperature and flow fields. The effect of added nanotubes and Cu nanoparticles on flow and temperature fields of the Water (the base fluid) is presented in Figure 3 for the open cavity with 
The presented values for maximum stream-function shows that adding the 1% volume fraction of Carbon nanotube-nanoparticles increase the maximum value of stream- function about 57%, 59% and 75% respectively for 

Although, the Cu nanoparticles have higher density, the results show that Carbon nanotube-nanoparticles have more positive effects on flow field of the base fluid. The Figure 4 presents the variation of velocity components of Carbon nanotube-nanofluid at horizontal mid-section of the cavity are shown for different Rayligh numbers and volume fraction of the added nanotubes when the aspect ratio is equal to unity. It is visible that adding nanoparticles to the base fluid has more obvious effects at high Rayligh numbers. At studying of convection problems in 2D cavities, aspect ratio of the cavity must be mentioned as characteristic parameter of the cavity. Therefore, the streamlines and temperature contours of the base fluid and Carbon nanotube-nanof- luid (



Figure 3. Streamlines and temperature contours of the base fluid, SWCNT and Cu-nanofluid (




Figure 4. Effect of different volume fractions of nanotubes on u-velocity (a) and v-velocity (b) in horizontal mid-section of the cavity at different 



Figure 5. Streamlines and temperature contours of the base fluid, Carbon nanotube and Cu-nanofluid (



The overall view of this figure shows that the increase of cavity’s aspect ratio leads to reduce of flow strength. The distance between hot and cold side in an enclosure is one of most important parameter of natural convection regime, the increase of this distance change the natural convection regime to a conduction manner in the problem domain.
6. Conclusions
The effect of Carbon nanotube and Cu nanoparticles on natural convection heat transfer in an open-end enclosure was studied numerically. The problem was investigated at different aspect ratios of the cavity (

Results show that adding a low value of Carbon nanotube to the base fluid led to significant enhancement of convection heat transfer.
The heat transfer rate is at closed relation with thermal conductivity of the suspensions therefore the use of nanoparticles with better thermal conductivity leads to better heat transfer enhancement at base fluid.
Make a comparison between Carbon nanotube and Cu-nanoparticles shows that the Carbon nanotube-nanoparticle has better performance to enhance convection rate.
The aspect ratio of the cavity plays an important role on natural convection heat transfer. An increase of this parameter leads to heat transfer reduction in a 2D deep open cavity.
Rayligh number loses its importance on natural convection in the high aspect ratios.
Cite this paper
Keshtkar, M.M. (2016) Simulation of Natural Convection Heat Transfer Enhancement by Nanoparticles in an Open-Enclosure Using Lattice Boltzmann Method. Advances in Nanoparticles, 5, 187-198. http://dx.doi.org/10.4236/anp.2016.54020
References
- 1. Xuan, Y. and Roetzel, W. (2000) Conceptions for Heat Transfer Correlation of Nanofluids. International Journal of Heat and Mass Transfer, 43, 3701-3707.
http://dx.doi.org/10.1016/S0017-9310(99)00369-5 - 2. He, Y., Qi, C., Hu, Y., Qin, B. and Ding, Y. (2011) Lattice Boltzmann Simulation of Alumina-Water Nanofluid in a Square Cavity. Nanoscale Research Letters, 6, 184-193.
http://dx.doi.org/10.1186/1556-276X-6-184 - 3. Patel, H.E., Pradeep, T., Sundararajan, T. and Das, S.K. (2005) A Micro Convection Model for Thermal Conductivity of Nanofluid. Pramana Journal of Physics, 65, 863-869.
http://dx.doi.org/10.1007/BF02704086 - 4. Sabbaghzadeh, J. and Ebrahimi, S. (2007) Effective of Thermal Conductivity of Nanofluids Containing Cylindrical Nanoparticles. International Journal of NanoScience, 6, 45-49.
http://dx.doi.org/10.1142/S0219581X07004286 - 5. Masoumi, N., Sohrabi, N. and Behzadmehr, A. (2009) A New Model for Calculating the Effective Viscosity of Nanofluids. Journal of Physics D: Applied Physics, 42, Article ID: 055501.
http://dx.doi.org/10.1088/0022-3727/42/5/055501 - 6. Talebi, F., Mahmoudi, A.H. and Shahi, M. (2010) Numerical Study of Mixed Convection Flows in a Square Lid-Driven Cavity Utilizing Nanofluid. International Communication in Heat and Mass Transfer, 37, 79-90.
http://dx.doi.org/10.1016/j.icheatmasstransfer.2009.08.013 - 7. Abu-Nadaa, E. and Chamkhac, A.J. (2010) Mixed Convection Flow in a Lid-Driven Inclined Square Enclosure Filled with a Nanofluid. European Journal of Mechanics B/Fluids, 29, 472-482.
http://dx.doi.org/10.1016/j.euromechflu.2010.06.008 - 8. Nemati, H., Farhadi, M., Sedighi, K. and Fattahi, E. (2010) Lattice Boltzmann Simulation of Nanofluid in Lid-Driven Cavity. International Communication in Heat and Mass Transfer, 37, 1528-1534.
http://dx.doi.org/10.1016/j.icheatmasstransfer.2010.08.004 - 9. Fattahi, E., Farhadi, M., Sedighi, K. and Nemati, H. (2012) Lattice Boltzmann Simulation of Natural Convection Heat Transfer in Nanofluids. International Journal of Thermal Sciences, 52, 137-144.
http://dx.doi.org/10.1016/j.ijthermalsci.2011.09.001 - 10. Javaran, E.J., Nassab, S.A.G. and Jafari, S. (2010) Thermal Analysis of a 2-D Heat Recovery System Using Porous Media Including Lattice Boltzmann Simulation of Fluid Flow. International Journal of Thermal Sciences, 49, 1031-1041.
http://dx.doi.org/10.1016/j.ijthermalsci.2009.12.004 - 11. Mousavi, S.E., Sedighi, K., Farhadi, M. and Fattahi, E. (2013) Lattice Boltzmann Simulation of Deformation and Breakup of a Droplet under Gravity Force Using Inter particle Potential Model. International Journal of Engineering, Transactions A: Basics, 26, 781-794.
- 12. Jafari, M., Farhadi, M. and Sedighi, K. (2012) Effect of Wavy Wall on Convection Heat Transfer of Water-Al2O3 Nanofluid in a Lid-Driven Cavity Using Lattice Boltzmann Method. International Journal of Engineering, Transactions A: Basics, 25, 165-175.
http://dx.doi.org/10.5829/idosi.ije.2012.25.02a.06 - 13. Mohamad, A. (2007) Applied Lattice Boltzmann Method for Transport Phenomena, Momentum, Heat and Mass Transfer. Sure, Calgary.
- 14. Mohamad, A.A., El-Ganaoui, M. and Bennacer, R. (2009) Lattice Boltzmann Simulation of Natural Convection in an Open Ended Cavity. International Journal of Thermal Sciences, 48, 1870-1875.
http://dx.doi.org/10.1016/j.ijthermalsci.2009.02.004 - 15. Javam, A. and Arm?eld, S.W. (2001) Stability and Transition of Stratified Natural Convection Flow in Open Cavities. Journal of Fluid Mechanics, 44, 285-303.
- 16. Gavili, A., Dallali Isfahani, T. and Sabbaghzadeh, J. (2011) The Variation of Heat Transfer in a Two-Sided Lid-Driven Differentially Heated Square Cavity with Nanofluids Containing Carbon Nanotubes for Physical Properties of Fluid Dependent on Temperature. International Journal for Numerical Methods in Fluids, 68, 302-323.
http://dx.doi.org/10.1002/fld.2507 - 17. Kim, P., Shi, L., Majumdar, A. and Mceuen, P.L. (2001) Thermal Transport Measurements of Individual Multi Walled Nanotubes. Physical Review Letters, 87, Article ID: 215502.
http://dx.doi.org/10.1103/PhysRevLett.87.215502 - 18. Berber, S., Kwon, Y.K. and Tomanek, D. (2000) Unusually High Thermal Conductivity of Carbon Nanotubes. Physics Review Letter, 84, 4613-4616.
http://dx.doi.org/10.1103/PhysRevLett.84.4613 - 19. Thostenson, E.T., Ren, Z. and Chou, T.W. (2001) Advances in the Science and Technology of Carbon Nanotubes and Their Composites: A Review. Composite Science Technology, 61, 1899-1912.
http://dx.doi.org/10.1016/S0266-3538(01)00094-X - 20. Iijima, S. and Ichihashi, T. (1993) Single-Shell Carbon Nanotubes of 1-nm Diameter. Nature, 363, 603-605.
http://dx.doi.org/10.1038/363603a0 - 21. Izadi, M., Behzadmehr, A. and Jalali-Vahida, D. (2009) Numerical Study of Developing Laminar Forced Convection of a Nanofluid in an Annulus. International Journal Thermal Science, 48, 2119-2129.
http://dx.doi.org/10.1016/j.ijthermalsci.2009.04.003 - 22. Mirmasoumi, S. and Behzadmehr, A. (2008) Numerical Study of Laminar Mixed Convection of a Nanofluid in A Horizontal Tube Using Two-Phase Mixture Model. Applied Thermal Engineering, 28, 717-727.
http://dx.doi.org/10.1016/j.applthermaleng.2007.06.019 - 23. Saleh, H., Roslan, R. and Hashim, I. (2011) Natural Convection Heat Transfer in a Nanofluid-Filled Trapezoidal Enclosure. International Journal Heat Mass Transfer, 54, 194-201.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2010.09.053 - 24. Gherasim, I., Roy, G., Nguyen, C.T. and Vo-Ngoc, D. (2009) Experimental Investigation of Nanofluids in Confined Laminar Radial Flows. International Journal Thermal Science, 48, 1486-1493.
http://dx.doi.org/10.1016/j.ijthermalsci.2009.01.008 - 25. Khanafer, K., Vafai, K. and Lightstone, M. (2003) Buoyancy-Driven Heat Transfer Enhancement in a Two-Dimensional Enclosure Utilizing Nanofluids. International Journal Heat Mass Transfer, 46, 3639-3653.
http://dx.doi.org/10.1016/S0017-9310(03)00156-X - 26. Choi, U.S. (1995) Enhancing Thermal Conductivity of Fluids with Nanoparticles, Developments and Application of Non-Newtonian Flows. ASME Journal of Heat Transfer, 66, 99-105.
- 27. Xie, H., Youn, H.W. and Choi, M. (2003) Nanofluids Containing Multiwalled Carbon Nanotubes and Their Enhanced Thermal Conductivities, Journal Applied Physics, 94, 4967-4973.
http://dx.doi.org/10.1063/1.1613374 - 28. Choi, S.U.S., Zhang, Z.G., Lockwood, F.E. and Grulke, E.A. (2001) Anomalous Thermal Conductivity Enhancement in Nanotube Suspensions. Applied Physics Letter, 79, 2252-2256.
http://dx.doi.org/10.1063/1.1408272 - 29. Jamshidi, N., Farhadi, M., Ganji, D.D. and Sedighi, K. (2012) Experimental Investigation on the Viscosity of Nanofluids. International Journal of Engineering -Transaction (B), 25, 201-209.
- 30. Eastman, J.A., Choi, S.U.S., Li, S. and Thompson, L.J. (2001) Anomalously Increased Effective Thermal Conductivities of Ethylene Glycol-Based Nanofluids Containing Copper Nanoparticles. Applied Physics Letter, 78, 718-724.
http://dx.doi.org/10.1063/1.1341218 - 31. Tiwari, R.K. and Das, M.K. (2007) Heat Transfer Augmentation in a Two-Sided Lid-Driven Differentially Heated Square Cavity Utilizing Nanofluids. International Journal Heat Mass Transfer, 50, 2002-2018.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2006.09.034 - 32. Marquis, F.D.S. and Chibante, L.P.F. (2005) Improving the Heat Transfer of Nanofluids and Nano Lubricants with Carbon Nanotubes. The Journal of the Minerals, Metals & Materials Society, 57, 57-32.










