American Journal of Plant Sciences
Vol.4 No.5(2013), Article ID:32108,9 pages DOI:10.4236/ajps.2013.45118
Effect of Air Content on the Oxygen Diffusion Coefficient wang#s:TopTitleof Growing Mediawang#e:TopTitle
![]()
Osnabrueck University of Applied Sciences, Osnabrueck, Germany.
Email: *r.anlauf@hs-osnabrueck.de
Copyright © 2013 Dominik Schmitz et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 16th, 2013; revised April 20th, 2013; accepted May 10th, 2013
Keywords: Gas Diffusivity; Pore Tortuosity; Air Capacity; Horticultural Substrate; Peat
ABSTRACT
An important parameter for describing oxygen availability in growing media is the air capacity, but this parameter does not include any information about the gas exchange with the surrounding atmosphere. The oxygen diffusion coefficient fulfills this requirement and may be better suited as a characteristic parameter to describe the oxygen regime. The measurement of the gas diffusion coefficient is a common method to describe the oxygenation in mineral soils, but this method has not been studied well on growing media yet. In this investigation four different growing media were used to measure the oxygen diffusion coefficient at two different bulk densities and four different water tensions in the laboratory. The effect of density and water tension on the oxygen diffusion coefficient in different growing media and the dependence on air content were investigated. The results show that both water tension and density have a major influence on oxygen diffusion. With increasing density and moisture content, a decrease of the oxygen diffusion coefficient can be observed. Between the substrates there are no significant differences regarding the oxygen diffusion coefficient at the same air content. Based on the oxygen diffusion coefficients of the substrates, the models describing the dependence of gas diffusion coefficients to air content in the literature were tested for the transferability to growing media. The Moldrup model [1] shows the best fit. The fit can be slightly further improved by modifying the tortuosity parameter.
1. Introduction
For the characterization of the chemical and physical properties of growing media, the parameters container capacity, air capacity as well as nutrient contents and nutrient storage capacity are most important [2-4]. Oxygen stress may induce a number of reactions in plants, such as a reduction in transpiration, nutrient uptake and growth [5]. Recently the meaningfulness of air capacity as the most important parameter describing oxygen supply to roots is discussed in the literature [6-9]. The air in growing media contains oxygen, carbon dioxide, nitrogen and water vapor. The oxygen concentration in the air in growing media can vary due to different oxygen consumption levels and different diffusion rates of atmospheric oxygen into the substrate. Thus, an inhibited gas exchange leads to reduced oxygen concentration. According to [10], the inhomogeneity of the pore distribution caused by compression can lead to strongly varying oxygen concentrations in the immediate vicinity. The air capacity, however, provides little information about the oxygen content in the root zone. The gas exchange between atmosphere and growing media is probably more important for the description of the oxygen supply to growing media than the air capacity [9, 11-13]. Primarily the air-filled continuous pores serve as a transport system for gas exchange. The rate of gas exchange is determined by the size and shape of these pores [4,14,15].
The determination of the oxygen diffusion coefficient played no major role in the analysis of growing media yet [16]. Investigations described in the literature are usually based on mineral soils [4,17].
Aims of this study were 1) to examine the effect of bulk density and water/air content of different horticultural growing media on the oxygen diffusion coefficient; 2) to evaluate the transferability of model functions relating the oxygen diffusion coefficient to air content in mineral soils to growing media; 3) to test if a better fit of these functions can be achieved by varying the tortuosity parameter describing the intricacy of the pore.
2. Theoretical Background
The air in growing media contains oxygen (O2), carbon dioxide (CO2), nitrogen (N2) and water vapor (H2O). The composition of air in growing media differs from the composition of atmospheric air (O2: 20.9%vol; CO2: 0.03%vol) by a higher concentration of carbon dioxide and water vapor and a lower content of oxygen [15,18]. The higher content of CO2 and lower content of O2 result from biological processes in the growing media, such as root respiration or microbial activity. In these processes oxygen is consumed and CO2 is produced. The consumed O2 and produced CO2 can be compensated only slowly by atmospheric air through diffusion. This explains the lower O2 content and increased CO2 content in soils and growing media [18,19].
According to Raviv and Lieth [4] the understanding of the gas transport mechanisms is essential for the evaluation of the aeration in growing media; however this has not been adequately examined yet. The air in growing media is rather humid and because of the root respiration and microbial activity it is also enriched with CO2. The O2 content runs in opposite direction to the CO2 content, because respirated oxygen is spent.
The diffusion coefficient of O2 in air (1.98 × 10−5 m2·s−1) is much larger than that in water (1.90 × 10−9 m2·s−1) [18]. The gas exchange can be reduced by water in the substrate which primarily occupies the smaller pores so that the gases are confined to the larger pores. At higher water contents typical for growing media, the water also occupies part of the coarse pores and, thus, strongly reduces the oxygen diffusion rate. Compaction usually decreases the coarse pores and leads to lower gas exchange rates [4]. Also the structure of the growing media is an important factor for gas exchange. Substrates containing smaller particles usually have less continuous pores and, therefore, smaller gas diffusion rates [4,19,20]. In soil air, CO2 is commonly 0.3% - 1% but can be much higher in warm soils with fresh organic matter [21]. Gruda et al. [22] indicate CO2 content in growing media of about 1.4%vol at high microbial activity and inhibited gas exchange. Soil O2 concentrations less than 10%vol indicate poor aeration [21].
For many gases in growing media sources and sinks are not precisely determined. For oxygen, however, the atmosphere is the source and the substrate is the sink. Therefore, the gas exchange between growing media and atmosphere is essential for the oxygen content and, thus, for the life of organisms and for plant growth in growing media [19].
The pore size is decisive for the intensity of the gas exchange between growing media and atmosphere [4]. The more macropores exist in growing media, the more gas exchange takes place between growing media and atmosphere. Small pore sizes and a disturbed continuity of pores act as a barrier to gas exchange [7,23].
Gas exchange can take place either through convection or diffusion. Convective gas exchange can occur due to barometric or temperature-related gas volume changes or flowing water. In total, however, the convective gas exchange is only about 10% of the total gas exchange; the rest of the gas exchange occurs by diffusion [18,19].
The diffusive gas exchange depends on the oxygen and carbon dioxide partial pressure. The higher CO2 partial pressure in the air of growing media results in a CO2 diffusion into the atmosphere. In contrast, the lower O2 partial pressure in the air of growing media performs to a diffusion of atmospheric oxygen into the growing media.
Diffusion is driven by concentration gradients. The flux of gases (JG) can be described with Fick’s law (Equation (1)) [4]:
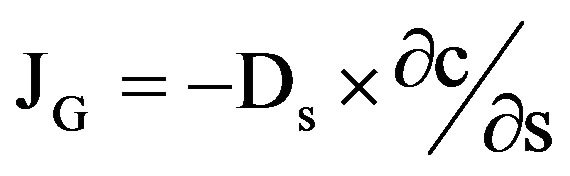 (1)
(1)
with the flux of gases JG [M∙L−2∙T−1], the gas concentration c [M∙L−3], the effective gas diffusion coefficient Ds [L−2∙T−1] and the diffusion length s [L].
The diffusion coefficient of soils Ds is often described in relation to the diffusion coefficient in free air Da. This ratio is the relative diffusion coefficient Ds/Da and has the advantage that it is independent of temperature, air pressure and type of gas [24]. The dependency of Ds/Da on air content and pore volume is described by different models developed for mineral soils. Different models have been compiled by several authors [17,25,26]. As natural soils have a different pore structure than growing media, the latter need different functions to describe the dependency of the oxygen diffusion coefficient on air content [27]. The applicability of different functions for growing media was tested in preceding studies of the authors of this investigation (unpublished data). The tests showed that the function of Moldrup [1] (Equation (2)) with the tortuosity parameter m = 6 fits best:
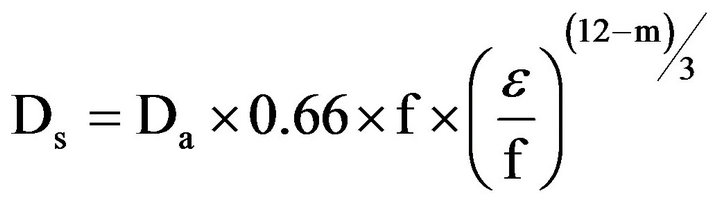 (2)
(2)
where Ds is the gas diffusion coefficient in the growing media [L2∙T−1], ε is the air content [L3∙L−3], Da is the gas diffusion coefficient in free air [L2∙T−1], f is the pore volume [L3∙L−3] and m a tortuosity parameter (3 for undisturbed soils or 6 for disturbed soils).
For the physical characterization of growing media different parameters are used. The pore volume (PV) is referred to as the proportion of the airand water-filled pore space in the total volume. The container capacity (CC) is the water content, which remains at a matric potential of −10 hPa in the medium. The air capacity (AC)
is the proportion of the pore volume, which is filled with air at a matric potential of −10 hPa [6].
3. Materials and Methods
Four types of commercially available growing media in two densities and four moisture levels were prepared (Table 1).
The standard substrate density (SSD) was determined by a standard method [28]. Since considerable substrate shrinking after wetting and drying to the required pF levels was observed in preliminary tests, densities of SDD plus 10% and SDD plus 20% were used which practically showed no more shrinking. Prior to measuring the oxygen diffusion coefficient, the substrate samples were filled with the respective densities to the double rings described in DIN EN 13041 [29]. In this study only the lower ring was required, because a defined density was set.
The water tension of the media was adjusted to pF 0.5, 1.0, 1.5 and 1.8 using an Eijkelkamp standard sand box apparatus [29,30]. After measuring the oxygen diffusion coefficient, the substrates were oven dried at 105˚C and the air content was calculated as the difference between pore volume and water content.
The physical properties of the growing media used were characterized as pore volume (PV), container capacity (CC) and air capacity (AC) (Table 2). There are

Table 1. Experimental variants.
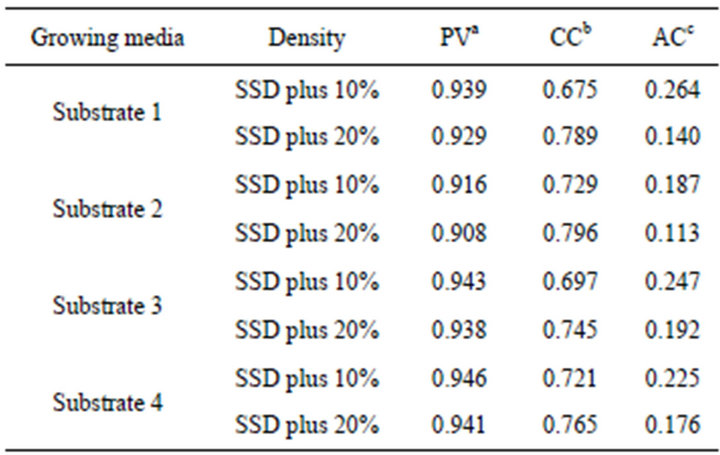
Table 2. Physical characteristics of the growing media for the different densities used (cm3∙cm−3).
a. Pore Volume; b. Container Capacity; c. Air Capacity differences in their hydraulic characteristics due to the different composition of the growing media. An increase in density is accompanied by an increase in the container capacity and a decrease in the air capacity. Substrates 1 and 3 (peat/perlite and peat/coconut fibre/compost) had the highest air capacity whereas substrate 2 (peat/clay) had the lowest.
The particle size distribution of each substrate was determined according to DIN 11540 [31], with a set of eight sieves with a mesh size of 0.2 mm to 31.5 mm. Portions of substrate samples remaining on each screen were weighed and expressed as the percentage of total sample weight. The mean weight diameter (MWD) was calculated using Equation (3) [32]:
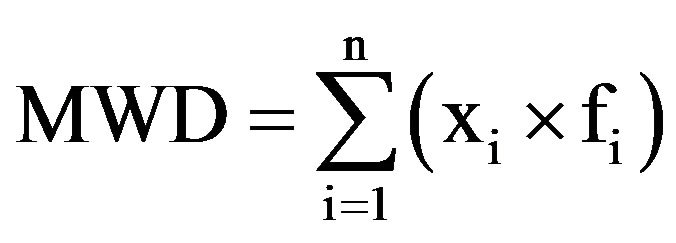 (3)
(3)
with the number of classes n, the average particle size fi and the mass retained on the sieve divided by the total medium mass xi.
Substrate 3 is the one with the finest particles, the lowest proportion of coarse particles larger than 2 mm (35.7%) and the smallest MWD (3.2 mm). The other substrates used have a proportion of coarse particles and a MWD of 44.4% and 4.7 mm (substrate 4), 50.0% and 4.5 mm (substrate 2) and 62.9% and 5.7 mm (substrate 1), respectively (Table 3).
The equipment used to measure the oxygen diffusion coefficient is based on the principle of Rolston and Moldrup [33]. Similar equipment was used for rockwool and perlite [34] and for peat based substrates [35]. The device is shown schematically in Figure 1: the measuring equipment consists of a PET container with a volume of 5390 cm3,
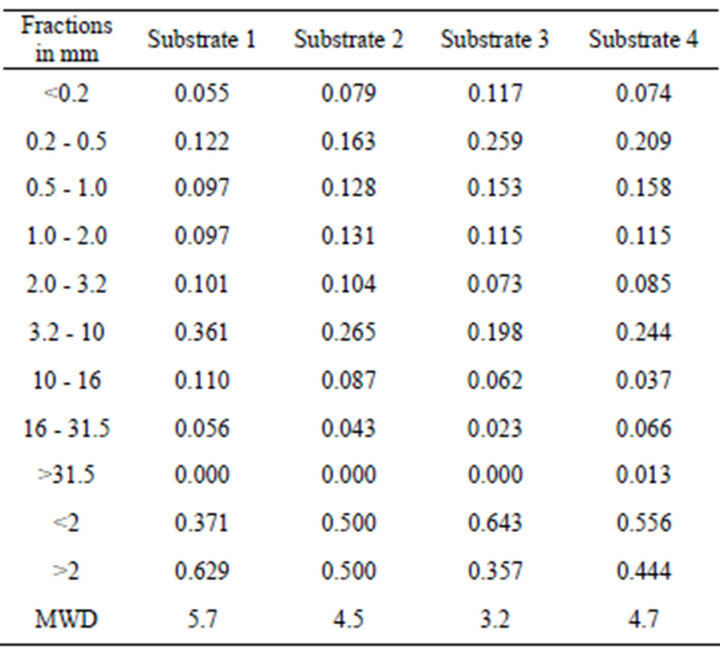
Table 3. Particle size distribution of the four different growing media (g∙g−1).
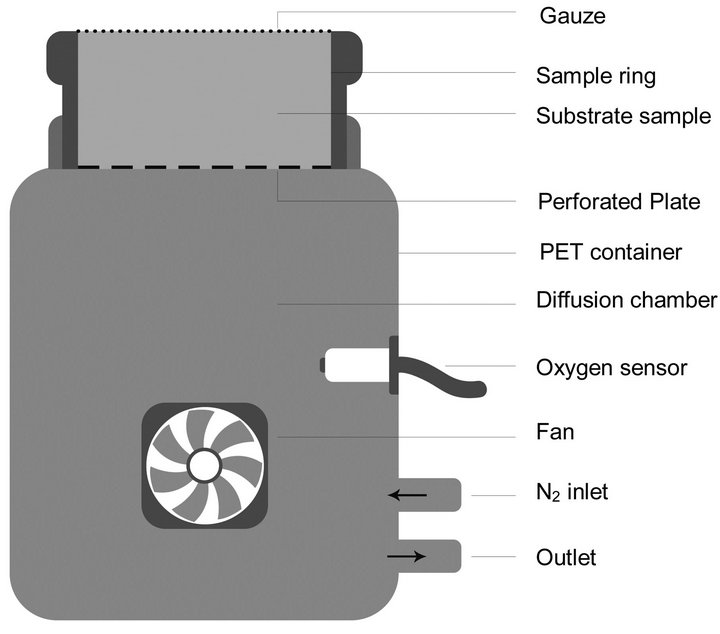
Figure 1. Schematic illustration of the measuring equipment.
which is the diffusion chamber. On a highly perforated plate in the screw cap the sample is placed with the sample ring (383 cm3). The diffusion chamber contains an oxygen sensor connected to a data logger which records the oxygen concentration in the chamber every minute. Furthermore, there is an inlet and outlet for filling the diffusion chamber with nitrogen prior to the measurement, so that the oxygen concentration is about 1 % at the beginning of the measurement. A very slow fan inside the diffusion chamber provides sufficient turbulence of the gases.
The measurement is based on the formation of a gas concentration gradient within the substrate sample, i.e. between low O2 concentration in the diffusion chamber (Ci) and the constant high O2 concentration in the laboratory (Ca). Oxygen diffuses due to the concentration gradient. The oxygen diffusion coefficient can be calculated based on the change of oxygen concentration in the chamber per unit time [33].
The calculation of the oxygen diffusion coefficient is derived from the 1. Fick’s law (Equation 1). Based on Equation (1), the oxygen diffusion through the substrates can be described as [33] (Equation (4)):
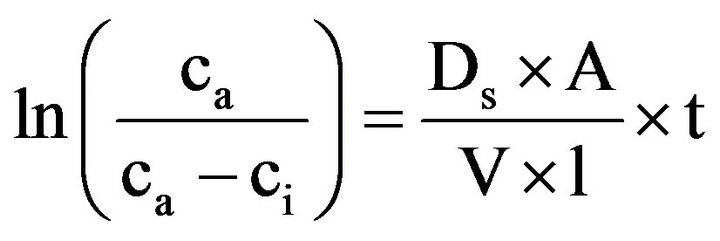 (4)
(4)
where Ca is the O2 concentration in the laboratory [%vol], t is the time [s], Ci the concentration in the chamber [%vol], V the volume of the diffusion chamber [cm3], Ds the Diffusion coefficient [cm2∙s−1], l the height of the substrate sample [cm] and A the cross sectional area [cm2].
Equation 4 represents a mathematical linearization. By plotting the left part of the equation versus time (t), the slope ms = ln (Ca/(Ca - Ci))/t can be calculated. Consequentially, the oxygen diffusion coefficient can be calculated as Ds = V·l·ms/A.
This procedure could involve two potential sources of error: At the very beginning of the measurement the slope of the evaluation function is not linear. This could be solved by evaluating only the data between 20 and 120 minutes after the start of the measurement where the function was always linear. Another possible source of error could be the O2 consumed within the growing media. However, the amount of O2 consumed in the sample in two hours was very small in relation to the amount of O2 diffusing through the sample due to the high concentration gradient. Therefore, no effect of the O2 consumption on the O2 diffusion coefficient is expected.
The statistical analysis was performed using the statistical program IBM SPSS Statistics 20, with a multifactorial analysis of variance. The conditions of normal distribution and homogeneity of variance were first checked with the Kolmogorov-Smirnoff test and the Levene test [36]. After taking the logarithm of the oxygen diffusion coefficient the conditions for the analysis of variance could be met.
4. Results
Figure 2 shows the oxygen diffusion coefficient and air content of the studied substrates and the respective moisture level (average of both density variations).The oxygen diffusion coefficient rises with decreasing moisture content. The diffusion coefficient at a very wet range (pF 0.5) is close to zero, but substrate 1 has a significantly higher gas diffusion coefficient. At moisture level pF 1.0, the oxygen diffusion coefficients are significantly higher. Between pF 1.5 and 1.8 there are no significant differences, only substrate 3 in moisture level pF 1.5 is significantly lower than the other substrates.
The relationship between air content and moisture level looks similar; air content rises with decreasing moisture levels. At moisture level pF 0.5 the air content of substrate 1 is the highest. The air contents at moisture level pF 1.0 are significantly higher, but there are no differences between the substrates. Between the moisture levels pF 1.5 and pF 1.8 there are no significant differences, except substrate 3 in moisture level pF 1.5 (lower) and substrate 1 in moisture level pF 1.8 (higher).
An analysis of variance shows that the factors density and air content (moisture level) have a significant influence on the oxygen diffusion coefficient. The tested substrates have no significant influence on the oxygen diffusion coefficient.
Figure 3 confirms that there is a strong relationship between oxygen diffusion coefficient and air content. The oxygen diffusion coefficient increases with increasing air content. Between the different substrates there are
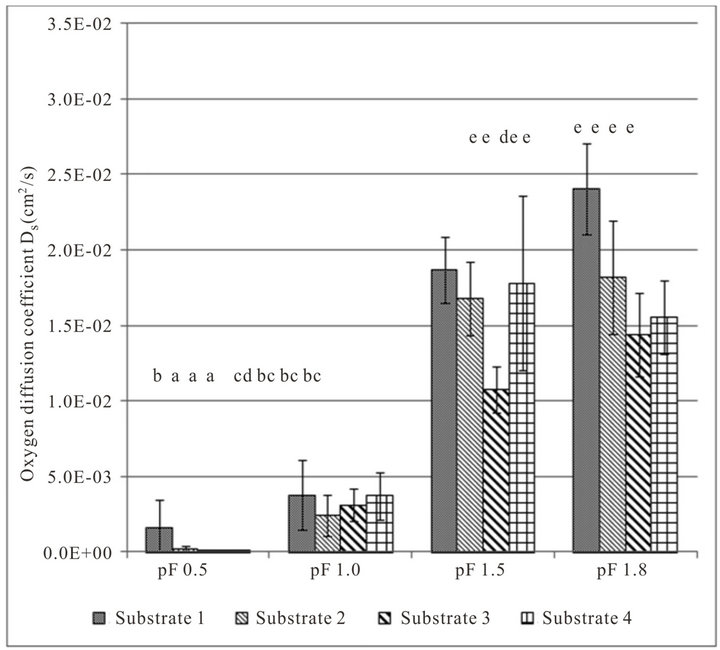
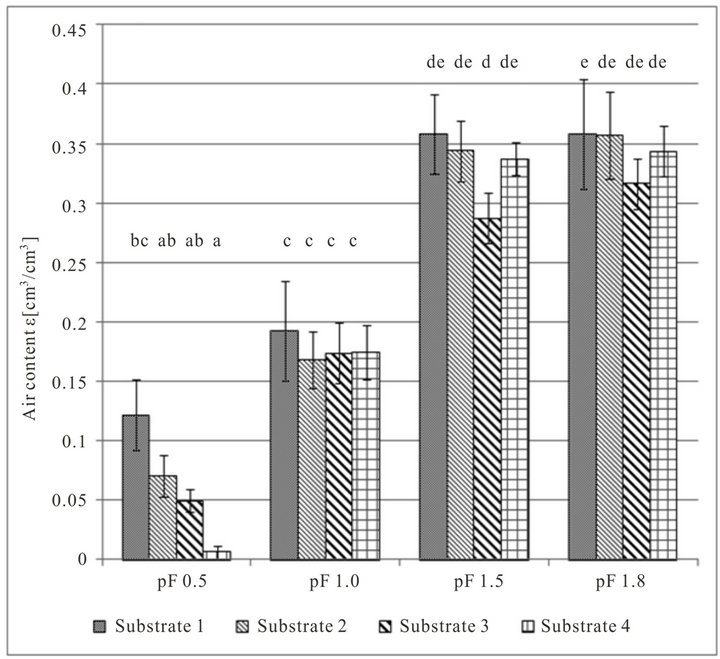
Figure 2. Measured oxygen diffusion coefficients Ds (top) and air content ε (bottom) of growing media at different pF values (average of both densities). Error indicator: confidence interval; classes of homogeneity: Tukey test.
no considerable differences (ANOVA, p < 0.05) but the measured values differ in their statistical scattering.
The fitted tortuosity parameters m are different for the four tested substrates, but with values from 6.0 to 6.5 they lie close together. Fitting the tortuosity parameter to the data only slightly increases the quality of the regression of the oxygen diffusion coefficient to air content. Considering all measured values of the four tested substrates the tortuosity parameter m = 6.3 has the best fit (not shown in the figure).
Figure 4 shows the effect of the different densities on the gas diffusion coefficients.
The fitted curves are different for the two densities. Density has an effect on air content and, thus, on the oxygen diffusion coefficient (ANOVA, p < 0.05). The scattering of the lower density is higher than that of the higher density. The fitted tortuosity parameters are different for both densities, but the values of 6.4 (SSD plus 10%) and 6.0 (SSD plus 20 %) lie close together.
5. Discussion
The measurement equipment used in this study based on Rolston and Moldrup [33] was checked with external replications and in other studies with different growing media [37,38] and proved to be suitable for measuring the oxygen diffusion coefficient in growing media.
The results in this study are similar to those of other authors [35,39,40] with respect to the dependence of the oxygen diffusion coefficient on water content and density. Increasing density and moisture content leads to a decreasing oxygen diffusion coefficient. This can be explained by the fact that also the air content decreases with increasing density and increasing moisture content. The good correlation between air content and oxygen diffusion coefficient might be restricted to the fine materials tested in this study. Caron et al. [41] showed less correlation between both parameters with coarse materials (pine bark, 10 - 20 mm). Peat fragments are porous particles, while bark is rather impermeable and acts as a barrier for the gas exchange [41]. However, the typical growing media for horticultural production which may have problems with oxygen supply are fine textured materials.
In a previous study with two types of growing media the oxygen diffusion coefficient did not differ for different types of growing media at the same air content [37]. This is in accordance with the results in this study with four

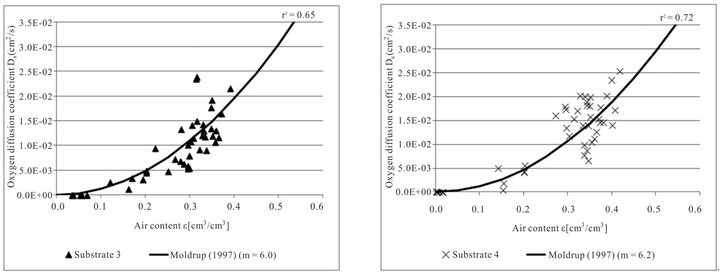
Figure 3. Measured oxygen diffusion coefficients Ds in relation to air content ε and the function of Moldrup et al. (1997) for substrate 1 (n = 51), substrate 2 (n = 56), substrate 3 (n = 44) and substrate 4 (n = 44) for both density variations.
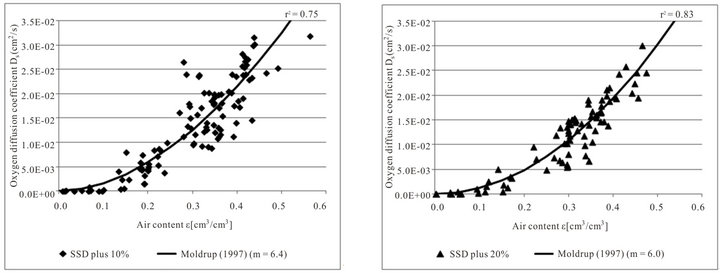
Figure 4. Measured oxygen diffusion coefficients Ds depending on air content ε and function of Moldrup et al. (1997) with SSD plus 10% (n = 111) and SSD plus 20% (n = 84) (SSD: standard substrate density).
types of substrates. The oxygen diffusion coefficient at different pF values differs between substrate 3 and the others (Figure 2). Substrate 3 has the lowest mean weighted diameter (Table 3) and, therefore, the lowest air content at the given pF values.
Thus, the choice of the type of growing media has no primary effect on the oxygen supply in the root zone, at least at the same air content. The oxygen diffusion coefficient and, therefore, the oxygen supply are more influenced by cultivation measures such as irrigation system and compression of growing media because these cultivation activities affect the air content of growing media.
The very good description of the dependence of the oxygen diffusion coefficient to air content with the model of Moldrup et al. [1] can be explained by the fact that the tortuosity parameter m = 6 is adapted to disturbed soils. Disturbed soils have a similar pore structure than growing media and, therefore, this model function suits growing media very well. Even fitting the tortuousity parameter m to optimize the adjustment to the measured data did not show a considerable improvement. The fitted parameters in this study were between m = 6.0 and m = 6.5 and, thus, very close to the original value of m = 6.0. With higher compression the tortuosity parameter is exactly 6.0. The tortuosity parameter describes the intricacy of the pore system, an increasing tortuosity results in a lower tortuosity parameter. In more compacted growing media the tortuosity of the pores is similar to artificially compacted mineral soils. This is the reason why the tortuosity parameter is lower in compacted than in less dense substrates. With an additional change of the factor 0.66 (Equation (2)) an even better fit would be possible.
The measured oxygen diffusion coefficients in this study are in accordance with literature results. [35] measured relative gas diffusion coefficients Ds/Da between 7 × 10−3 and 23.9 × 10−3 in growing media at a matric potential of −8 hPa. [40] measured relative gas diffusion coefficient Ds/Da between 0.2 × 10−3 and 34.1 × 10−3 in growing media at matric potentials from 0 to −10 hPa. [39] found relative gas diffusion coefficients of 10·10-3 in peat at matric potentials between 5 and 15 hPa. The relative oxygen diffusion coefficients measured in this study are in a similar range (0 to 53.1 × 10−3). [40] measured a relative gas diffusion coefficient Ds/Da of 34.1 × 10−3 at an air content of 0.26 cm3cm−3. In this study the relative gas diffusion coefficient Ds/Da is about 37.2 × 10−3 (n = 2) at an air content of 0.25 to 0.276 cm3cm−3, which is very close to the results of [40]. These results indicate that the dependency of the oxygen diffusion coefficient on air content is similar for a wide range of growing media and may, therefore, be used to describe aeration for potted plants if the air content is known.
The dependency of the oxygen diffusion coefficient on density and air content supports the assumption that air capacity is not an adequate parameter to describe the oxygen supply in growing media [9,11-13]. Air capacity is not an indicator for the actual air content in growing media. It only describes the standardized air storage capacity of growing media at moisture level pF 1.0, but there is no information about oxygen supply. Using a parameter such as the oxygen diffusion coefficient would be more adequate to describe the oxygen supply in growing media. The water and air content of growing media can be described by simulation models where, however, detailed information on the hysteretic pF curves of the growing media is required [6]. If this information is available, the combination of a simulation model describing water and air content with the oxygen diffusion coefficient as a parameter could be a relatively simple way to analyze oxygen deficiencies under practical greenhouse growers conditions.
6. Conclusion
The results of this study show that the oxygen diffusion coefficient depends on water content and substrate density, which both influence air content of growing media. There is a stable dependency of the oxygen diffusion coefficient on air content irrespective of the type of growing media. This relation can be described by the model function of Moldrup [41]. Future studies should clarify a possible modification of the tortuosity parameter at different compaction levels. Together with techniques to describe the air content of growing media, such as simulation models, this dependency could be used to develop estimation procedures for oxygen supply for different practical situations in horticultural production.
REFERENCES
- P. Moldrup, T. Olesen, D. E. Rolston and T. Yamaguchi, “Modeling Diffusion and Reaction in Soils: Vii. Predicting Gas and Ion Diffusivity in Undisturbed and Sieved Soils,” Soil Science, Vol. 162, No. 9, 1997, pp. 632-640. doi:10.1097/00010694-199709000-00004
- M. De Boodt and O. Verdonck, “The Physical Properties of the Substrates in Horticulture,” Acta Horticulturae, Vol. 26, 1972, pp. 37-44. http://www.actahort.org/books/26/26_5.htm
- F. Göhler and H. D. Molitor, “Erdelose Kulturverfahren im Gartenbau,” Eugen Ulmer Verlag, Stuttgart, 2002.
- M. Raviv and J. H. Lieth, “Soilless Culture-Theory and Practice,” Elsevier, Amsterdam, 2008.
- R. Baas and M. G. Warmenhoven, “Alcohol Dehydrogenase Indicating Oxygen Deficiency in Chrysanthemum Grown in Mineral Media,” Acta Horticulturae, Vol. 401, 1995, pp. 273-282. http://www.actahort.org/books/401/401_33.htm
- R. Anlauf, P. Rehrmann and H. Schacht, “Simulation of Water Uptake and Redistribution in Growing Media during Ebb-and-Flow Irrigation,” Journal of Horticulture and Forestry, Vol. 4, No. 1, 2012, pp. 8-21.
- J. Caron and N. V. Nkongolo, “Aeration in Growing Media: Recent Developments,” Acta Horticulturae, Vol. 481, 1999, pp. 545-551. http://www.actahort.org/books/481/481_64.htm
- J. Caron, P. Morel, L. M. Riviére and G. Guillemain, “Identifying Appropriate Methodology to Diagnose Aeration Limitations with Large Peat and Bark Particles in Growing Media,” Canadian Journal of Soil Science, Vol. 90, No. 3, 2010, pp. 481-494. doi:10.4141/CJSS09015
- A. Wrede, “Untersuchungen zur Ermittlung der Kennwerte des Luftund Wasserhaushalts von Kultursubstraten,” Ph.D. Thesis, Hannover University, Hannover, 2010. http://edok01.tib.uni-hannover.de/edoks/e01dh01/331191490.pdf
- H. G. Frede, “Der Gasaustausch des Bodens,” Göttinger Bodenkundliche Berichte, Vol. 87, 1986.
- S. E. Allaire, J. Caron, J. Duchesne, L. E. Parent and J. A. Rioux, “Air-Filled Porosity, Gas Relative Diffusivity, and Tortuosity: Indices of Prunus x Cistena sp. Growth in Peat Substrates,” Journal of the American Society for Horticultural Science, Vol. 121, 1996, pp. 236-242. http://journal.ashspublications.org/content/121/2/236.full.pdf
- M. Raviv, R. Wallach and T. J. Blom, “The Effect of Physical Properties of Soilless Media on Plant Performance: A Review,” Acta Horticulturae, Vol. 644, 2004, pp. 251-259. http://www.actahort.org/books/644/644_34.htm
- L. M. Riviere and J. Caron, “Research on Substrates-State of the Art and Need for the Coming 10 Years,” Acta Horticulturae, Vol. 548, 2001, pp. 29-41. http://www.actahort.org/books/548/548_1.htm
- N. C. Brady and R. R. Weil, “Elements of the Nature and Properties of Soils,” Prentice-Hall, London, 1999.
- W. A. Jury and R. Horton, “Soil Physics,” John Wiley, Hoboeken, 2004.
- J. Caron, L. M. Riviére and G. Guillemain, “Gas Diffusion and Air-Filled Porosity: Effect of Some Oversize Fragments in Growing Media,” Canadian Journal of Soil Science, Vol. 85, No. 1, 2005, pp. 57-65. doi:10.4141/S03-086
- P. Moldrup, T. Olesen, S. Yoshikawa, T. Komatsu and D. E. Rolston, “Three-Porosity Model for Predicting the Gas Diffusion Coefficient in Undisturbed Soil,” Soil Science Society of America, Vol. 68, No. 3, 2004, pp. 750-759.
- D. Hillel, “Environmental Soil Physics,” Academic Press, London, 1998.
- K. Handreck and N. Black, “Growing Media for Ornamental Plants and Turf,” University of New South Wales Press, Sydney, 2002.
- O. Verdonck and P. Demeyer, “The Influence of the Particle Sizes on the Physical Properties of Growing Media,” Acta Horticulturae, Vol. 644, 2004, pp. 99-101. http://www.actahort.org/books/644/644_10.htm
- R. E. Sojka and H. D. Scott, “Aeration Measurement,” In: In: R. Lal, Ed., Encyclopedia of Soil Science, 2nd Edition, CRC Press, Rattan Lal, 2005. doi:10.1201/NOE0849338304.ch8
- N. Gruda, T. Rocksch and U. Schmidt, “CO2-Concentration in Root Zone of Vegetables, Cultivated in Organic Substrates,” Acta Horticulturae, Vol. 801, 2005, pp. 1063- 1068. http://www.actahort.org/books/779/779_64.htm
- N. V. Nkongolo and J. Caron, “Bark Particle Size and Modification of the Physical Properties of Peat Substrate,” Canadian Journal of Soil Science, Vol. 79, No. 1, 1999, pp. 111-116. doi:10.4141/S96-084
- J. Gliński and W. Stępniewski, “Soil Aeration and Its Role for Plants,” CRC Press, Boca Raton, 1985.
- R. Lal and M. K. Shukla, “Principles of Soil Physics,” Marcel Dekker, Inc., New York/Basel, 2004.
- P. Moldrup, T. Olesen, J. Gamst, P. Schjoenning, D. E. Rolston and T. Yamaguchi, “Predicting the Gas Diffusion Coefficient in Repacked Soil: Water-Induced Linear Reduction Model,” Soil Science Society of America, Vol. 64, No. 5, 2000, pp. 1588-1594. doi:10.2136/sssaj2000.6451588x
- M. A. Mostafid, C. Shanka, P. T. Imhoff and R. Yazdani, “Gas Transport Properties of Compost-Woodchip and Green Waste for Landfill Biocovers and Biofilters,” Chemical Engineering Journal, Vol. 191, 2012, pp. 314-325. doi:10.1016/j.cej.2012.03.022
- VDLUFA, “Bestimmung der Rohdichte (Volumengewicht) von gärtnerischen Erden und Substraten ohne Sperrige Komponenten. VDLUFA Methodenbuch, Band I, Die Untersuchung von Böden,” VDLUFA Verlag, Darmstadt, 1991.
- DIN EN 13041, “Soil Improvers and Growing MediaDetermination of Physical Properties-Dry Bulk Density, Air Volume, Water Volume, Shrinkage Value and Total Pore Space,” German Version EN 13041:2010, Deutsches Institut für Normung e.V., Beuth Verlag, 2010.
- R. Gabriels and O. Verdonck, “Physical and Chemical Characterization of Plant Substrates: Towards a European Standardization,” Acta Horticulturae, Vol. 294, 1991, pp. 249-259. http://www.actahort.org/books/294/294_27.htm
- DIN 11540, “Peats and Peat Products for Horticulture and Landscape Gardening-Test Methods, Properties, Specifications,” Deutsches Institut für Normung e.V., Beuth Verlag, 2005.
- W. D. Kemper and R. C. Rosenau, “Aggregate Stability and Size Distribution,” In: A. Klute, Ed., Methods of Soil Analysis, Part 1 (2nd Edition), Agrononomy Monograph Nr. 9, American Dairy Science Association und Soil Science Society of America, Madison, 1986, pp. 425-441.
- D. E. Rolston and P. Moldrup, “Gas Diffusivity,” In: A. Klute, Ed., Methods of Soil Analysis, Part 4, Soil Science Society of America, Madison, 2002, pp. 1089-1102.
- R. Baas, G. Wever, A. J. Koolen, E. Tariku and K. J. Stol, “Oxygen Supply and Consumption in Soilless Culture: Evaluation OD an Oxygen Simulation Model for Cucumber,” Acta Horticulturae, Vol. 554, 2001, pp. 157-164. http://www.actahort.org/books/554/554_16.htm
- J. Caron and N. V. Nkongolo, “Assessing Gas Diffusion Coefficients in Growing Media from in Situ Water Flow and Storage Measurements,” Vadose Zone Journal, Vol. 3, 2004, pp. 300-311. doi:10.2113/3.1.300
- G. W. Snedecor and W. G. Cochran, “Statistical Methods,” Iowa State University Press, Ames, 1980.
- Y. Rondot, “Effect of Water Content and Bulk Density on the Oxygen Diffusion in Horticultural Substrates (in German),” Diploma Thesis, Osnabrueck University of Applied Sciences, Osnabrueck, 2009.
- D. Schmitz, “Effect of Bulk Density and Water Content of Different Growing Media on Oxygen Diffusion Coefficients (in German),” B.Sc. Thesis, Osnabrueck University of Applied Sciences, Osnabrueck, 2011.
- P. Cannavo and J. C. Michel, “Peat Particle Size Effects on Spatial Root Distribution, and Changes on Hydraulic and Aeration Properties,” Scientia Horticulturae, Vol. 151, 2013, pp. 11-21. doi:10.1016/j.scienta.2012.12.021
- J. A. King and K. A. Smith, “Gaseous Diffusion through Peat,” Journal of Soil Science, Vol. 38, No. 2, 1987, pp. 173-177. doi:10.1111/j.1365-2389.1987.tb02134.x
- J. Caron, P. Morel and L. M. Riviére, “Aeration in Growing Media Containing Large Particle Size,” Acta Horticulturae, Vol. 548, 2001, pp. 229-234. http://www.actahort.org/books/548/548_25.htm
NOTES
*Corresponding author.

