International Journal of Nonferrous Metallurgy
Vol.04 No.04(2015), Article ID:61474,9 pages
10.4236/ijnm.2015.44005
Electromagnetic Braking of Natural Convection during Ohno Continuous Casting of an Industrial Aluminum Alloy
Simbarashe Fashu
Department of Materials Science and Engineering, Harare Institute of Technology, Harare, Zimbabwe

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 7 October 2015; accepted 22 November 2015; published 25 November 2015

ABSTRACT
With the purpose of obtaining compositionally uniform ingots during Ohno continuous casting of a dilute industrial aluminum alloy through eliminating segregation due to convection, a magnetic field strength required to damp natural convection and suppress macrosegregation was numerically determined. This was achieved by solving conservation equations of continuity, momentum, energy and Maxwell’s equations in order to predict the magnetic field effects on flow field (determining macrosegregation). The electromagnetic field was applied orthogonally to the natural convection flow. Through this approach, the optimum magnetic field strength required to damp natural convection and establish diffusion controlled solute transport of the alloy during solidification was established.
Keywords:
Static Magnetic Field, Braking, Convection, Damping, Buoyancy

1. Introduction
Ohno Continuous Casting (OCC) process is a recently developed heated mold unidirectional continuous casting process used for producing superior, unidirectional rods and wires of substantial length [1] . When producing single crystal/unidirectional ingots during Ohno continuous casting, it is an ideal practice to remove natural melt convection entirely, leading to solidification heat transfer by pure conduction. This is because convective flow in the melt leads to fluctuations in the solute concentration in the produced ingot (macrosegregation) [2] . So, one would aim to be able to grow a single crystal with a planar interface and a quiescent melt near the solid-liquid interface where solute transport is merely through diffusion [3] [4] . Elimination of melt convection maintains a stable planar solid-liquid interface thereby minimizing the solid ingot defect densities and compositional variations [5] . A practical approach to reduce convective mixing in the melt is through application of static direct current (DC) magnetic fields to suppress buoyancy induced flows under full gravity [6] - [12] . The effect of an externally imposed uniform magnetic field differs according to the flow pattern of the convective flow considered [13] .
Electromagnetic damping of melt flow is mostly used in steel continuous casting and crystal growth industries. In continuous casting of steel, electromagnetic brakes employ coils with direct current to generate a static magnetic field to affect flow in the mold cavity [7] [9] . Several researchers investigated the use of electromagnetic damping to control natural convection during solidification. Early experiments by Hurle [14] and Utech and Flemings [15] showed that striations in tellurium doped indium antimonide grown in a horizontal furnace by directional solidification due to natural convection can be eliminated by the application of a DC magnetic field. Harvey et al. [16] used a vertical DC magnetic field during solidification of tellurium-doped indium antimonidein a horizontal boat and showed that the use of magnetic field eliminated the solute bands that are formed in absence of magnetic field. The study by Oreper and Szekely [17] shows that the magnetic field suppresses natural convection currents and the magnetic field strength is one of the most important factors to achieve the desired control. Rudraiah et al. [18] numerically investigated the effect of a transverse magnetic field on natural-convection flow inside a rectangular cavity with isothermal vertical walls and adiabatic horizontal walls and found out that a circulating flow is formed with a relatively weak magnetic field and that the convection is suppressed when the magnetic field strength increases. Motakef and Kim [19] , Adornato and Brown [20] used numerical simulation in a vertical Bridgman-Stockbarger configuration and demonstrated the dissipative influence of the applied magnetic field on the intensity of convection in the melt. The effect of a strong vertical magnetic field on convection and segregation in the vertical Bridgeman crystal growth process was considered by Ben Hadid et al. [21] .
Recently, Gunzberger et al. [22] estimated the optimal magnitude of the constant magnetic field necessary for the suppression of turbulent flow in the melt. Thus, numerical simulations are nearly irreplaceable means to get detailed information about the flow field and the magnetic fields in order to optimize the processes. In this paper, numerical simulation is used, for the first time, to determine the optimum magnitude of the constant (DC) magnetic field required to damp natural convection during Ohno continuous casting of a dilute industrial aluminum alloy. Although in conventional continuous casting processes, suppression of the convective cell near the solid- liquid interface results in an increase in the slope of the diffusion controlled boundary layer, which can lead to constitutional super cooling [5] , the use of a heated mold considered here during OCC avoids under cooling.
2. Mathematical Model
2.1. Flow, Temperature and Solidification Fields Modeling
The solidification process was modeled by using the governing equations based on the mixture theory originally from Benon and Incropera [23] . The Boussinesq form is used and gravity acts in the y-direction aligned with the magnetic field and perpendicular to casting direction (Figure 1).
2.1.1. Assumptions
In the solidification system considered in this work, the following assumptions are used regarding the transport of heat, mass, and momentum:
i. The thermal and physical properties are constant within each phase.
ii. The solid and liquid phases are in local thermodynamic equilibrium, i.e. the phase diagram applies.
iii. The liquid metal is considered to be an incompressible Newtonian fluid.
iv. The Boussinesq approximation can be invoked.
v. Since the concentration of the solutes in the industrial aluminum alloy considered is very small; the buoyancy is mainly due to temperature gradient (thermal convection is only considered).
vi. Electromagnetic property of the melt was assumed to be uniform and isotropic.
2.1.2. Mass Conservation Equation
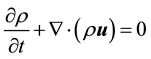 (1)
(1)
Figure 1. The horizontal Ohno continuous casting process in presence of electromagnetic braking.
where 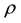 is the density of the mixture,
is the density of the mixture, 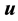 is the superficial velocity.
is the superficial velocity.
2.1.3. Momentum Conservation Equation
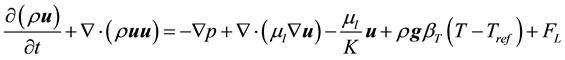 (2)
(2)
where p is the pressure, 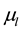 is the dynamic viscosity of the melt,
is the dynamic viscosity of the melt, 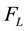 is the momentum source due to magnetic braking,
is the momentum source due to magnetic braking,  corresponds to the nominal temperature of the mold which is 938 K.
corresponds to the nominal temperature of the mold which is 938 K.
2.1.4. Energy Conservation Equation
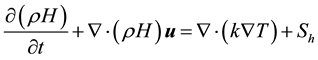 (3)
(3)
where H is the enthalpy, k is thermal conductivity; T is temperature and
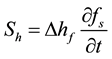 (4)
(4)
is the source term due to heat released during solidification.
The liquid and solid enthalpies are related through the following thermodynamic relations:
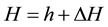 (5)
(5)
where 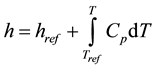 and
and 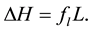
Cp is the specific heat and href is the reference enthalpy. In order to account for the release of latent heat during solidification in the energy equation, the enthalpy method was used in this work.
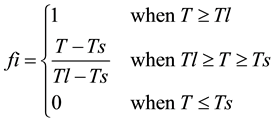 (6)
(6)
where Tl and Ts are the liquidus and solidus temperatures respectively. The release of latentheat within the mushy region was properly incorporated in the energy equation as a source term.
The mixture quantities are defined in the following manner:
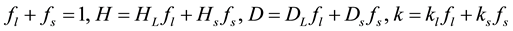
where fl is liquid fraction, fs is solid fraction and D is for diffusion coefficient.
2.2. Electromagnetic Field
The basic mechanism for the interaction of an applied magnetic field and the molten metal involves the electrical currents induced by the movement of the conductor in presence of a magnetic field. This interaction results in the Lorentz force which is used to damp and control the convective flow. The method for solving for the electromagnetic force is derived from Ohm’s law and Maxwell’s equation [24] . Thus, a magnetic field is induced when a conducting fluid, such as molten metal, moves through an applied magnetic field, B0with a velocity, u. This induced field, b is calculated by solving:

With

From the solved magnetic field B, the current density j can be calculated using Ampere’s relation as:

The Lorentz force, or induced electromagnetic force, is determined using:

This force term is subsequently added into the momentum equations as a source/sink term. Under the assumption of low magnetic Reynolds number

where J is the current density.
2.3. Physical Model
Figure 1 shows the horizontal Ohno continuous casting process domain considered in presence of electromagnetic braking magnets. The heated mold is used to keep the molten metal temperature above the liquidus temperature, and the solid ingot is pulled from the melt with pinch rollers. Water spraying is used to control the temperature and position the solid-liquid interface at the mold exit. Electromagnetic brakes are placed next to the molten metal and adjusted to control melt convection.
2.4. Numerical Procedure
The governing equations are discretized in CFD Fluent 6.3.26 using an implicit, first-order upwind scheme and the SIMPLE algorithm for pressure-velocity coupling. The momentum and energy source terms for thermal convection and enthalpy release during solidification are incorporated in the governing equations using User Defined Functions (UDFs). Lorentz forces are computed using the magnetic induction method and is then added into the momentum equations as a source term at the next iteration step. To simulate the continuous extraction of the solidifying aluminum rods, the shell wall boundaries are given a downward velocity equal to the casting speed of 1 mm/min. The thermo-physical properties of the industrial aluminum used are given in Table 1 and the simulation initial and boundary conditions are given in Table 2.
Table 1. Thermo physical properties of Al 0.12 wt.% Cu 0.11 wt.% Si Alloy.
Table 2. Initial and boundary conditions.
3. Results and Discussion
3.1. Validation of the Model
The ability of the CFD Fluent 6.3.26 magnetic induction method to predict convective flow braking during continuous casting was validated by K. Cukierski and B. Thomas using caster experiments [9] . Armor et al. [23] also used the model in CFX to compute electromagnetic braking of flow during LPD growth of SiGe crystals. The results are shown in Figure 2 and clearly demonstrate the effect of braking magnetic fields in suppressing convection flow. Here the flow fields are reduced in strength as the electromagnetic fields are increased from 0.0 T to 0.2 T.
3.2. Solidification and Flow Fields (in Presence and Absence of Electromagnetic Braking)
The numerical results of the investigation of buoyancy-driven convection during OCC of aluminum in presence and absence of an applied magnetic field are presented here. The effect of natural convection on flow fields was first simulated numerically. Then the electromagnetic intensity required to completely suppress the flow was determined by increasing its strength until the entire flow convection was suppressed. The temperature and solidification profiles for a steady OCC process are shown in Figure 3 and Figure 4, respectively. The gravity acts in the y-direction and is therefore aligned with the magnetic field. Figure 5 shows the computed natural convection velocity field within the melt in the heated mold region in absence of a magnetic field. The maximum velocity magnitude is around 0.006 m/s.
Figure 6 shows the computed velocity field in the heated mold region in presence of a uniform magnetic field of 0.05 T. The maximum velocity is on average approximately 0.000115 m/s. Increasing the magnetic field intensity to 0.1 T produces almost suppressed melt convection as shown in Figure 7 with a maximum velocity of approximately 0.0000311 m/s which is of the order of the casting speed (0.0000166 m/s) used. Thus, the magnetic field has completely suppressed the vortices that were present in the cases without the magnetic field. This case demonstrates that thermal buoyancy-induced flow intensity can be significantly reduced through the use of


Figure 2. Effect of braking electromagnetic fields on the flow fields, (a) No magnetic fields; (b) B = 0.1 T and (c) B = 0.2 T [23] .
Figure 3. Computed temperature profile for (g = 9.81 m/s2) and B = 0.0 T.
Figure 4. Computed solidification profile for (g = 9.81 m/s2) and B = 0.0 T.
Figure 5. Computed velocity magnitudes for (g = 9.81 m/s2) and B = 0.0 T.
Figure 6. Computed velocity magnitudes for (g = 9.81 m/s2) and B = 0.05 T.
Figure 7. Computed velocity magnitudes for (g = 9.81 m/s2) and B = 0.1 T.
applied magnetic fields, even under full gravity. Based on the effect of magnetic intensity on the performance of magnetic flow modifier, it can be concluded that an intensity of 0.1 T is the optimum value in designing the magnetic breaking system under the conditions considered here.
4. Conclusion
The electromagnetic field strength required to dampnatural melt flow during Ohno continuous casting in order to minimize macrosegregation was determined through numerical simulation. This was achieved by applying braking electromagnetic fields orthogonally to the natural convection flow. The computational results indicate different flow-field patterns in presence and absence of electromagnetic braking. The melt flow intensity decreased with increase in magnetic field intensity from zero and at the magnetic field intensity of around 0.1 T, the convection flow was completely suppressed. Using the optimized magnetic field strength, the number of coil windings and length of the coil for braking can be determined analytically making the process cheap to operate.
The design can be done using:
the coil windings and L = is the length of the coil. This optimum direct current (DC) electromagnetic intensity makes it possible to produce homogeneous ingots whilst the caster operates at minimum costs.
Cite this paper
SimbarasheFashu, (2015) Electromagnetic Braking of Natural Convection during Ohno Continuous Casting of an Industrial Aluminum Alloy. International Journal of Nonferrous Metallurgy,04,37-45. doi: 10.4236/ijnm.2015.44005
References
- 1. Ohno, A. (1986) Continuous Casting of Single Crystal Ingot by the OCC Process. Journal of Metals, 38, 14-16.
- 2. Ganapathysubramanian, B. and Zabaras, N. (2005) On the Control of Solidification Using Magnetic Fields and Magnetic Field Gradients. International Journal of Heat and Mass Transfer, 48, 4174-4189. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2005.04.027
- 3. Hof, B., Juel, A. and Mullin, T. (2003) Magneto-hydrodynamic Damping of Convective Flows in Molten Gallium. Journal of Fluid Mechanics, 482, 63-179.
- 4. Ganapathysubramanian, B. and Zabaras, N. (2004) Using Magnetic Field Gradients to Control the Directional Solidification of Alloys and the Growth of Single Crystals. Journal of Crystal Growth, 270, 255-272. http://dx.doi.org/10.1016/j.jcrysgro.2004.06.020
- 5. Watring, D.A. and Lehoczky, S.L. (1996) Magne-to-Hydrodynamic Damping of Convection during Vertical Bridgman- Stockbarger Growth of HgCdTe. Journal of Crystal Growth, 167, 478-487. http://dx.doi.org/10.1016/0022-0248(96)00279-5
- 6. Bojarevics, A., Cramer, A., Gelfgatand, Y.U. and Gerbeth, G. (2006) Experiments on the Magnetic Damping of an Inductively Stirred Liquid Metal Flow. Experiments in Fluids, 40, 257-266. http://dx.doi.org/10.1007/s00348-005-0065-x
- 7. Lei, H., Zhang, H. and He, J. (2009) Flow, Solidification, and Solute Transport in a Continuous Casting Mold with Electromagnetic Brake. Chemical Engineering & Technology, 32, 991-1002. http://dx.doi.org/10.1002/ceat.200800346
- 8. Tian, X., Zou, F., Li, B. and He, J. (2010) Numerical Analysis of Coupled Fluid Flow, Heat Transfer and Macroscopic Solidification in the Thin Slab Funnel Shape Mold with a New Type EMBr. Metallurgical and Materials Transactions B, 40, 112-120. http://dx.doi.org/10.1007/s11663-009-9314-3
- 9. Cukierski, K. and Thomas, B. (2008) Flow Control with Local Electromagnetic Braking in Continuous Casting of Steel Slabs. Metallurgical and Materials Transactions B, 39, 94-107. http://dx.doi.org/10.1007/s11663-007-9109-3
- 10. Mechighel, H. and Kadja, M. (2007) External Horizontally Uniform Magnetic Field Applied to Steel Solidification. Journal of Applied Sciences, 7, 903-912. http://dx.doi.org/10.3923/jas.2007.903.912
- 11. Wei, J.A., Zheng, L. and Zhang, H. (2009) Suppression of Melt Convection in a Proposed Bridgman Crystal Growth System. International Journal of Heat and Mass Transfer, 52, 3747-3756. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2009.02.029
- 12. Battira, M. and Bessaih, R. (2008) Three-Dimensional Natural Convection in the Horizontal Bridgman Configuration under Various Wall Electrical Conductivity and Magnetic Field. Numerical Heat Transfer, Part A: Applications, 55, 58-76. http://dx.doi.org/10.1080/10407780802603113
- 13. Gelfgat, A. and Yoseph, P. (2001) The Effect of an External Magnetic Field on Oscillatory Instability of Convective Flows in a Rectangular Cavity. Physics of Fluids, 13, 2269-2278. http://dx.doi.org/10.1063/1.1383789
- 14. Hurle, D. (1966) Temperature Oscillations in Molten Metals and Their Relationship to Growth Striae in Melt-Grown Crystals. Philosophical Magazine, 13, 305-310. http://dx.doi.org/10.1080/14786436608212608
- 15. Utech, H.P. and Flemings, M.C. (1966) Elimination of Solute Banding in Indium Antimonide Crystals by Growth in a Magnetic Field. Journal of Applied Physics, 37, 2021-2024. http://dx.doi.org/10.1063/1.1708664
- 16. Utech, H.P. and Flemings, M.C. (1967) Thermal Convection in Metal-Crystal Growth—Effect of a Magnetic Field. Journal of Physics and Chemistry of Solids, 28, 651.
- 17. Oreper, H.P. and Szekely, J. (1984) The Effect of a Magnetic Field on Transport Phenomena in a Bridgman-Stock-barger Crystal Growth. Journal of Crystal Growth, 67, 405-419. http://dx.doi.org/10.1016/0022-0248(84)90033-2
- 18. Rudraiah, N., Barron, R.M., Venkatachalappa, M. and Subbaraya, C. (1995) Effect of a Magnetic Field on Free Convection in a Rectangular Enclosure. International Journal of Engineering Science, 33, 1075-1084. http://dx.doi.org/10.1016/0020-7225(94)00120-9
- 19. Motakef, S. (1990) Magnetic Field Elimination of Convective Interference with Segregation during Vertical-Bridgman Growth of Doped Semiconductors. Journal of Crystal Growth, 104, 833-850. http://dx.doi.org/10.1016/0022-0248(90)90109-X
- 20. Kim, D.H., Adornato, P.M. and Brown, R.A. (1988) Effect of Vertical Magnetic Field on Convection and Segregation in Vertical Bridgman Crystal Growth. Journal of Crystal Growth, 89, 339-356. http://dx.doi.org/10.1016/0022-0248(88)90419-8
- 21. Ben Hadid, H., Henry, D. and Kaddeche, S. (1997) Numerical Study of Convection in the Horizontal Bridgman Configuration under the Action of a Constant Magnetic Field. Part 1. Two-Dimensional Flow. Journal of Fluid Mechanics, 333, 23-56. http://dx.doi.org/10.1017/S0022112096004193
- 22. Gunzberger, M., Ozugurlu, E., Turner, J. and Zhang, H. (2002) Controlling Transport Phenomena in the Czochralski Crystal Growth Process. Journal of Crystal Growth, 234, 47-62. http://dx.doi.org/10.1016/S0022-0248(01)01635-9
- 23. Bennon, D. and Incropera, F.P. (1987) A Continuum Model for Momentum, Heat and Species Transport in Binary Solid-Liquid Phase Change Systems—I. Model Formulation. International Journal of Heat and Mass Transfer, 30, 2161-2170. http://dx.doi.org/10.1016/0017-9310(87)90094-9
- 24. Fluent Inc. (2006) User’s Guide. 6.3.26 Version, Fluent Inc., New York.








