Computational Water, Energy, and Environmental Engineering
Vol.04 No.04(2015), Article ID:60840,10 pages
10.4236/cweee.2015.44006
Calibration of a Rainfall-Runoff Model to Estimate Monthly Stream Flow in an Ungauged Catchment
Shahrbanou Firouzi1*, Mohamad B. Sharifi2
1Synthesis and Balance Department, Northern Khorasan Regional Water Authority, Bojnord, Iran
2Faculty of Civil Engineering, Ferdowsi University of Mashhad, Mashhad, Iran
Email: *sfiroozi1001@Gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 September 2015; accepted 27 October 2015; published 30 October 2015
ABSTRACT
Simulation of runoff in ungauged catchments has always been a challenging issue, receiving significant attention more importantly in practical applications. This study aims at calibration of an Artificial Neural Network (ANN) model which is capable to apply in an ungauged basin. The methodology is applied to two sub-catchments located in the Northern East of Iran. To examine the effect of physical characteristics of the catchment on the capability of the model generalization, it is attempted to synthesize effective parameters using empirical methods of runoff estimation. Firstly, the model was designed for a pilot sub-catchment and the statistical comparison between simulated runoff, and target depicted the capability of ANN to accurately estimate runoff over a catchment. Then, the calibrated model was generalized to another sub-catchment assumed as an ungauged basin while there are runoff data to compare the result. The result showed that the designed model is relatively capable to estimate monthly runoff for a homogenous ungauged catchment. The method presented in this study in addition to adding effective spatial parameters in simulation runoff and calibration of model by using empirical methods and the integration of any useful accessible data, examines the adaptability of model to an ungauged catchment.
Keywords:
Artificial Neural Network (ANN), Ungauged Catchments, Spatial Parameters

1. Introduction
Uncertainty in hydrologic predictions makes it difficult to accurately estimate runoff which is a key factor in terms of catchment hydrology researches as well as practical management of water resources. Different types of the modern rainfall-runoff models which need complex parameters and data have been developed to provide reliable results whereas the feasibility of these models has been almost always concerned with ungauged or scarcely gauged catchments. Hence, application of data-driven techniques such as data mining and computational intelligence to describe dynamics and nonlinear process of rainfall-runoff has become the subject of increasing attention. Accordingly, Artificial Neural Network (ANN) has been widely applied as an efficient technique which is capable to capture the nonlinearity of rainfall-runoff process and represent the complexity of converting rainfall to runoff process over a catchment. So far, extensive researches have been done to examine the efficient performance of ANN models in simulation and prediction of stream flow. The efficiency of artificial neural network and multivariate regression was compared in prioritizing climate factors affecting runoff generation and concluded that multi-layer perceptron artificial neural network models are more accurate than multivariate regression models [1] . ANN approach was also employed for modelling rainfall-runoff due to typhoon in Taiwan [2] . It is interesting to note that the rainfall-runoff was simulated using ANN Coupled with Singular Spectrum Analysis [3] . Moreover, several ANN algorithms have been compared and generated separate ANN models for each season [4] , concluding that ANNs are promising tools not only in accurate modeling of complex processes but also in providing insight from the learned relationship, which would assist the modeler in understanding of the process under investigation as well as in evaluation of the model [5] . Some other studies have been done to examine the capability of ANNs with improving input data and under different situations of basins. As a case in point, it is attempted to train artificial neural networks using information-rich segments in long-time series [6] or consider a periodicity component (month enumerator) as an input to the ANN models to predict monthly stream flow [7] . In addition, a few researchers have looked to train ANNs on one basin and make predictions in another [7] [8] which can be considered as an appropriate technique to simulate runoff in data scarce catchments; hence the predictive results can be improved by forecasting at the sub-catchment rather than the entire catchment scale (due to spatial variation of rainfall) [9] . The American Society of Civil Engineers (ASCE) Task Committee has summarized applications of ANN for the solution of different hydrologic issues [10] . In the present study, two sub-catchments were considered where the methodology was applied, one as a pilot catchment and the other as an assumed unguaged catchment. The ANN model trained and calibrated in the pilot basin is applied to estimate the runoff over the assumed unguaged catchment. The details of the method used in the study and the results are briefly described.
2. Materials and Methods
2.1. Study Area
The model was applied in two sub-catchments of Samalghan River located in the East North region of Iran where the boundaries can be given by longitudes from 37˚24'39'' to 37˚29'07'' east and latitudes 56˚59'60'' to 56˚37'46'' north. The river is a tributary of Atrak River which flows into the Caspian Sea. Two sub catchments were delineated based Digital Elevation Model (DEM) in GIS software (Figure 1). The sub-catchments boundaries were defined by the location of the hydrometric stations installed in the lowest point of study area and physical characteristic of catchments, which play a significant role in formation of runoff, were calculated (Table 1). There are two rain gages and a climate station in the study area which provided monthly rainfall and
Table 1. Physical characteristics of the pilot and ungauged catchments.
aCalculated by  where P is the perimeter of the basin and A is the area [11] .
where P is the perimeter of the basin and A is the area [11] .
temperature data series which span the period of 35 years from 1978 to 2013. Rivers in the study area are fed by spring discharge and individual rain events. There are also two hydrometric stations which provide monthly runoff data in the mentioned period (Figure 2). Data time series were standardized prior to apply by subtracting
Figure 1. Location of delineated catchments of the study area.

Figure 2. The hydrometric stations in the outlet of (a) pilot and (b) unguaged catchment
the mean and dividing by the standard deviation. As mentioned above, one specific basin was considered as the pilot basin where the model was trained and calibrated and the other one regarded as an assumed ungauged catchment where the calibrated model applied to estimate runoff and the result compared with the observed data.
2.2. Artificial Neural Network Structure
The most commonly used ANN structure in hydrological applications is the feed-forward multilayer perceptron (MLP) (Figure 3). It consists of three layers; an input layer, a hidden layer, and an output layer. Neurons of each layer are connected to the neurons of the next layer by weights. Optimal values of these connection weights are obtained in training stage. The MLP is usually trained using the error back propagation algorithm, in which the inputs are presented to the network and the outputs obtained from the network are compared with the real output values (target values) of the system under investigation in order to compute error and then the computed error is back-propagated through the network and the connection weights are updated [5] [12] - [15] . In order to provide adequate training, network efficiency was evaluated during the training and validation stages, as suggested by Rajurkar et al. [9] . In this case, if the calculated errors of both stages keep decreasing, the training period is increased. This is continued to the point of the training stage error starting to decrease while the validation stage error starting to increase. At this point, training is stopped to avoid overtraining and optimal weights and biases are determined [9] [16] .
It is interesting to note that, in ANN simulation coupled with Levernberg-Marquardt training algorithm and hyperbolic tangent transfer functions, the appropriate choice of data set for training and testing stages is the most sensitive issue bringing about an efficient model which is capable to estimate monthly runoff in different seasons. In the present study, the standardized data series for two catchments are categorized into three data subsets, 60% of the entire data series for training set, the 20% of the data is considered as cross-validation set and the 20% of remaining data is used for testing set, considered based on the MATLAB tutorial.
2.3. Physiographic Characteristics
The most important controller feature in forming of surface runoff over a catchment is the physiographic characteristics including slope, main waterway length, soil type and vegetation cover which can be regarded as the spatial parameters. To improve the capability of the model generalization, it is attempted to make a connection between the spatial parameters and temporal rainfall events in form of synthetic input variables of ANN.
This is investigated by using empirical methods of runoff estimation which consider some spatial parameters and connect them with the average rainfall. Empirical models include relationships and equations which have been determined using analysis of limited data and the region characteristics, and the models are used to estimate some special probabilistic parameters. Most of these methods are useful for a special zone so, it is not possible to use them for other areas. But, some of these methods have more expanded domain and can be used for some same regions by applying some corrections and choosing proper coefficients [17] . In this study, im-
Figure 3. Structure of feed-forward Multilayer Perceptron (MLP).
portant conventional equations were evaluated in regional conditions of the study area and the results were com- pared with observations runoff hence four methods that provide the most acceptable results in the study area were selected as the major equations, employing to synthesize the input data of ANN model as spatial-temporal variables. These equations are presented in the following:
Khosla proposed Equation (1) to calculate runoff using temperature and rainfall parameters [18] .
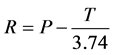 (1)
(1)
Lacy presented Equation (2) for estimating annual runoff based on reviews in several catchments [19] .
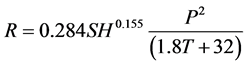 (2)
(2)
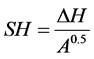 (2-1)
(2-1)
Justin investigated extensively on the relationships between annual rainfall and runoff in many catchments with different climatic conditions and presented their results as Equation (3) [20] .
 (3)
(3)
The Irrigation Department of India presented following equation between average rainfall and river runoff [21] .
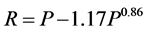 (4)
(4)
All variables in above equations are defined as the following:
P: average rainfall (cm); R: the corresponding runoff; T: average air temperature; A: catchment area (km); ΔH: maximum elevation difference of catchment; F: rainfall duration parameter; Z: coefficient for vegetation.
In the pilot catchment, in fact, the input factor of ANN model is the monthly runoff calculated based on the equations mentioned above in a period of 35 years and the output target is also monthly runoff values recorded by the hydrometric station at the outlet of Darkesh sub-catchment (Table 2).
Table 2. Description of input and output variables.
3. Discussion
The accuracy of ANN model performance is commonly evaluated with some efficiency terms. Each term is estimated from the predicted values of the model and the observed targets as follows:
1) The correlation coefficient (R-value) has been widely used to evaluate the goodness-of-fit of hydrologic and hydrodynamic models. This is obtained by performing a linear regression between the ANN-predicted values and the targets and is computed by Equation (4).
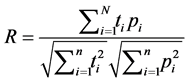 (4)
(4)
where R is correlation coefficient, N is the number of samples, 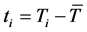 ,
, 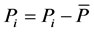 ,
, 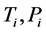 are the target and predicted values for
are the target and predicted values for 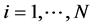 and, are the mean values of the target and predicted data set, respectively.
and, are the mean values of the target and predicted data set, respectively.
The correlation coefficient provides a direct measure of the ability of a model to reproduce the recorded flows with R = 1.0 indicating that all the estimated flows are the same as the recorded flows [22] .
2) The ability of the ANN-predicted values to match observed data is also evaluated by the Mean Square Error (MSE) defined as Equation (5) [23] .

The ANN responses are more precise if R, MSE are found to be close to 1, 0, respectively. In the present study, R and MSE, which demonstrate the performance efficiencies of each trial, have been recorded and compared to attain the more accurate results. The results of the three-layer feed-forward MLP model with synthesized input vectors for the pilot (Darkesh) catchment is shown in Figures 4-6. The comparison of calculated runoff by ANN model and the observed runoff (for stages of training, validation and testing) is also shown in Figures 7-9.
Figure 4. Observed versus simulated runoff for the Training stage.
Figure 5. Observed versus simulated runoff for the Validation stage.
Figure 6. Observed versus simulated runoff for the Testing stage.
Figure 7. Simulated and observed runoff at Training period.
Figure 8. Simulated and observed runoff at Validation period.
Figure 9. Simulated and observed runoff at Testing period.
Regression between the network result and the recorded monthly runoff in the pilot basin presents an appropriately satisfactory correlation between the observed runoff data and simulated ones. The results are quite ac- ceptable and represent the satisfactory performance of the ANN model for the first catchment that means the model was successfully designed. Visual comparison of the estimated monthly runoff with actual values convince that the model capable to simulate the natural regime of stream.
Application of Calibrated Model in an Ungauged Catchment
The goodness-of-fit measures point out a satisfactory robustness for the ANN model over the first catchment. This ability of the ANN which in fact can be trained by available effective data and estimate monthly runoff opens new opportunities to dealing with the ungauged catchment issues. In the last part of the study, with regard to the capability and efficiency of the ANN model to simulate the monthly runoff in DARKESH sub-catchment
as the pilot study area, the important step is to apply the calibrated model to the SHIRABAD sub-catchment regarded as an ungauged basin. In order to apply the method, similar to the pilot catchment, the rain data and the physical characteristics of SHIRABAD basin were synthesized by empirical equations and entered to the calibrated model based on pilot catchment’s dataset and run the model.
The correlation parameter and the regression equation between the result of model and the observed runoff on SHIRABAD catchment (the observed runoff data are only used for assessment of result since the catchment is regarded as a ungauged catchment in terms of runoff data) is presented in the Figure 10 and a comparison of the estimated monthly runoff (in the period of 35 years) with actual values of recorded stream flow is also shown in Figure 11. As it can be seen, in some data sets, there are particular months with large differences between estimated and recorded runoff that have a dramatic effect on the coefficient of correlation. These differences demonstrate that the calibrated model is unable to estimate the particular extreme flood events which are immensely dependent on rainfall intensity, though the general regime of stream flow is quite recognized by the ANN model.
Figure 10. Recorded monthly runoff versus simulated mon- thly runoff over the ungauged catchment.
Figure 11. Recorded monthly runoff versus simulated monthly runoff over the ungauged catchment.
4. Conclusion
The procedure outlined in the study in addition to examining the capability of a MLP structure of ANN model, analyzed the effectiveness of synthesizing input vectors (using empirical methods) to simulate rainfall-runoff process on a catchment. The result indicates that if the effective parameters are entered to the model as the synthesized vectors, network learning process can be accelerated and improved so that the model becomes more capable to identify system and provide the more accurate result in face of new data. This ability is of great importance in generalization of model in an ungauged basin where there are no runoff data to training and validating the network. The result of this study represents the efficiency of ANN network in rainfall-runoff modeling, providing the accurate result in a pilot basin. In addition, in terms of application of model in an ungauged catchmenteven if the accuracy of results in comparison to the pilot catchment was declined, calibration of a model with appropriate cover of accessible climatic and spatial data which can be employed in adjacent and homogenous catchments would be an asset to estimate runoff in the absence of hydrological stations by considering the model estimating error.
Acknowledgements
The authors gratefully acknowledge the North Khorasan Water Regional Authority to provide data which have been used in this study. The corresponding author would like to express her great appreciation to Dr. FarshadKouhian, who made invaluable comments to conduct the study.
Cite this paper
Shahrbanou Firouzi,Mohamad B. Sharifi, (2015) Calibration of a Rainfall-Runoff Model to Estimate Monthly Stream Flow in an Ungauged Catchment. Computational Water, Energy, and Environmental Engineering,04,57-66. doi: 10.4236/cweee.2015.44006
References
- 1. Qaderi, M., Khaleqi, M., Taqi Dastani, M. and Saber Chenari, K. (2014) A Comparative Study of the Efficiency of Artificial Neural Network and Multivariate Regression in Prioritizing Climate Factors Affecting Runoff Generation in Research Plots. International Bulletin of Water Resources & Development, 2, 41-53.
- 2. Chen, S.M., Wang, Y.M. and Tsou, I. (2013) Using Artificial Neural Network Approach for Modelling Rainfall-Runoff Due to Typhoon. Journal of Earth System Science, 122, 399-405.
http://dx.doi.org/10.1007/s12040-013-0289-8 - 3. Wu, C.L. and Chau, K.W. (2011) Rainfall-Runoff Modelling Using Artificial Neural Network Coupled with Singular Spectrum Analysis. Journal of Hydrology, 399, 394-409.
http://dx.doi.org/10.1016/j.jhydrol.2011.01.017 - 4. Singh, P. and Deo, M.C. (2007) Suitability of Different Neural Networks in Daily Flow Forecasting. Applied Soft Computing, 7, 968-978.
http://dx.doi.org/10.1016/j.asoc.2006.05.003 - 5. Kalteh, A.M. (2008) Rainfall-Runoff Modelling Using Artificial Neural Networks (ANNs): Modelling and Understanding. Caspian Journal of Environmental Sciences, 6, 53-58.
- 6. Singh, S., Jain, S. and Bárdossy, A. (2014) Training of Artificial Neural Networks Using Information-Rich Data. Open Access Hydrology Journal, 1, 40-62.
http://dx.doi.org/10.3390/hydrology1010040 - 7. Kisi, O. (2008) River Flow Forecasting and Estimation Using Different Artificial Neural Network Techniques. Hydrology Research, 39, 27-40.
http://dx.doi.org/10.2166/nh.2008.026 - 8. Cigizoglu, H.K. (2003) Estimation, Forecasting and Extrapolation of River Flows by Artificial Neural Networks. Hydrological Sciences, 48, 349-361.
http://dx.doi.org/10.1623/hysj.48.3.349.45288 - 9. Rajurkar, M.P., Kothyari, C. and Chaube, U. (2004) Modeling of Daily Rainfall-Runoff Relationship with Artificial Neural Network. Journal of Hydrology, 285, 96-113.
http://dx.doi.org/10.1016/j.jhydrol.2003.08.011 - 10. ASCE Task Committee on Application of Artificial Neural Networks in Hydrology (2000) Artificial Neural Networks in Hydrology. II: Hydrologic Applications. Journal of Hydrologic Engineering, 5, 115-123.
http://dx.doi.org/10.1061/(ASCE)1084-0699(2000)5:2(115) - 11. Black, P.E. (1996) Water Hydrology. 2nd Edition, Lewis Publishers, New York.
- 12. Mutlu, E., Chaubey, I., Hexmoor, H. and Bajwa, S.G. (2008) Comparison of Artificial Neural Network Models for Hydrologic Predictions at Multiple Gauging Stations in an Agricultural Watershed. Hydrological Processes, 22, 5097-5106.
http://dx.doi.org/10.1002/hyp.7136 - 13. Sudheer, K.P., Gosain, A.K. and Ramasastri, K.S. (2002) A Data-Driven Algorithm for Constructing Artificial Neural Network Rainfall-Runoff Models. Hydrological Processes, 16, 1325-1330.
http://dx.doi.org/10.1002/hyp.554 - 14. Adamowski, J., Chan, H.F., Prasher, S.O. and Sharda, V.N. (2012) Comparison of Multivariate Adaptive Regression Splines with Coupled Wavelet Transform Artificial Neural Networks for Runoff Forecasting in Himalayan Microwatersheds with Limited Data. Journal of Hydroinformatics, 14, 731-744.
http://dx.doi.org/10.2166/hydro.2011.044 - 15. Asadi, A., Shahrabi, J. and Tabanmehr, S. (2013) A New Hybrid Artificial Neural Network for Rainfall-Runoff Process Modeling. Neurocomputing, 121, 470-480.
http://dx.doi.org/10.1016/j.neucom.2013.05.023 - 16. Chiang, Y.-M., Chang, L.C. and Chang, F.J. (2004) Comparison of Static-Feed Forward and Dynamic Feedback Neural Networks for Rainfall-Runoff Modeling. Journal of Hydrology, 290, 297-311.
http://dx.doi.org/10.1016/j.jhydrol.2003.12.033 - 17. Khosravi, K., Mirzai, H. and Saleh, I. (2013) Assessment of Empirical Methods of Runoff Estimation by Statistical Test (Case Study: Banadak Sadat Watershed, Yazd Province). International Journal of Advanced Biological and Biomedical Research, 1, 285-301.
http://www.ijabbr.com - 18. Khosla, A.N. (1949) Appraisal of Water Resources (Analysis and Utilization of Data). Proceedings of UNESCO Conference on the Conservation and Utilization of Resources, Lake Success, New York, 17 August-6 September 1949.
- 19. Garg, K.S. (2009) Irrigation Engineering and Hydraulic Structures. 23rd Edition, Khanna Publishers, Delhi.
- 20. Gupta, B.L. (1992) Engineering Hydrology. Second Edition, Standard Publishers, Delhi.
- 21. UPIRI (Uttar Pradesh Irrigation Research Institute) (1960) Rainfall-Runoff Studies for a Few Himalayan and Bundelkhand Catchments of Uttar Pradesh TM 30-PR (Hy-31).
- 22. Legates, D.R. and McCabe, G.J. (1999) Evaluating the Use of Goodness-of-Fit Measures in Hydrologic and Hydro-Climatic Model Validation. Water Resources Research, 35, 233-241.
http://dx.doi.org/10.1029/1998WR900018 - 23. Schaap, M.G. and Leij, F.J. (1998) Database Related Accuracy and Uncertainty of Pedotransfer Functions. Soil Science, 163, 765-779.
http://dx.doi.org/10.1097/00010694-199810000-00001












