Open Journal of Applied Biosensor
Vol.2 No.2(2013), Article ID:31239,10 pages DOI:10.4236/ojab.2013.22004
A Novel Design of Fuzzy PID Controllers for Dual-Sensor Cardiac Pacemaker Systems
Department of Engineering and Technology, University of Wisconsin-Stout, Menomonie, USA
Email: shiw@uwstout.edu
Copyright © 2013 Wei Vivien Shi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 22, 2013; revised March 1, 2013; accepted March 14, 2013
Keywords: Adaptation; Dual-Sensors; Fuzzy PID Controller; Heart Rate; Pacemaker
ABSTRACT
This work proposes to design a fuzzy proportional-integral derivative (FPID) controller for dual-sensor cardiac pacemaker systems, which can automatically control the heart rate to accurately track a desired preset profile. The combination of fuzzy logic and conventional PID control approaches is adopted for the controller design based on dual-sensors. This controller offers good adaptation of the heart rate to the physiological needs of the patient under different states (rest and walk). Through comparing with the conventional fuzzy control algorithm, FPID provides a more suitable control strategy to determine a pacing rate in order to achieve a closer match between actual heart rate and a desired profile. To assist the heartbeat recovery, the stimuli with adjustable pacing rate is generated by the pacemaker according to the FPID controller, such actual heart rate may track the preset heart rate faithfully. Simulation results confirm that this proposed control design is effective for heartbeat recovery and maintenance. This study will be helpful not only for the analysis and treatment of bradycardias but also for improving the performance of medical devices.
1. Introduction
CARDIOVASCULAR diseases are major causes of morbidity and mortality in the developed countries. One of the cardiac diseases, bradycardia sometimes results in fainting, shortness of breath, and if severe enough, death [1,2]. It is defined as a heart rate less than 60 bpm although it is seldom symptomatic until the rate drops below 50˚bpm [3]. This occurs because people with bradycardia may not be pumping enough oxygen to their own heart causing heart attack-like symptoms. It sometimes results in fainting, shortness of breath, and if severe enough, death [4]. In case of bradycardia, the electrical signals in the heart are ineffective to cause lower heart rate that is not enough for physiological needs, unless it is interrupted by an external stimulus generated by implantable cardiac devices, such as pacemakers, and then a normal heart rhythm is quickly restored.
With heart disease still the number one cause of death in the United States, the development and improvement of medical devices is of great importance. It is well known that pacemaker as one of the implantable cardiac devices for medical treatment of heart diseases has been widely used nowadays [5]. The complexity and reliability of modern pacemakers have increased significantlymainly due to developments in sensing technologies [6]. For the purpose of heart rate regulation, various types of sensors, such as activity sensor, metabolic sensor and dual-sensors, have been employed in pacemakers to detect the heart rate, body activity, and measure some consequence of a physiological change during exercise or facing environmental or emotional changes [7,8]. The information is then used to optimize the cardiac output through adjustment of the pacing rate.
In the absence of an ideal sensor, the employment of dual-sensors has been investigated [8]. Dual-sensors are used to avoid inappropriate rate increase and provide more accurate measurement of diagnostic data such that two sensors may compensate each other. The advantage of dual-sensors is not only for the rate control but also for other functions such as a) sensor cross-checking that increases the safety margin of the devices and b) the cardiac hemodynamic condition monitoring that is important for a mode switching. In this paper, one of the most common dual-sensors, combination of accelerometer and QT interval, is used to provide actual heart rate and activity signal. In cardiology, the QT interval is a measure of the time between the start of the Q wave and the end of the T wave in the heart’s electrical cycle.
An accelerometer placed in a pacemaker detects movement and patient’s physical activity requiring an increased heart rate and generates an electronic signal that is proportional to physical activity [9]. Accordingly, accelerometer estimates if a human body is at rest or taking a walk by detecting a patient’s physiological change and movement. This sensor is quick to respond but less physiologically accurate. Additionally, because of its non-metabolic response, it may pick up undesirable signals and miss other desirable ones.
On the other side, the QT interval sensor measures the interval between the pacing spike and the evoked T-wave of ECG signal to ensure the estimated state. It provides some consequence of physiological change and metabolic demand during walk or other conditions. QT interval rate response is physiologically accurate but slow to respond to the onset of moving. Consequently, to reduce these factors, two sensors are used to provide compensation, in that an ideal controller converges only when the system is stable.
Due to the uncertainties contain fuzzy or imprecise information by combining the physiological demand, fuzzy logic controller realization for the pacemaker systems has been developed [10]. Over the past two decades, the field of fuzzy controller applications broadened to include many industrial controls [11], and significant research work supported the development of fuzzy controllers.
However, the conventional control algorithm based on fuzzy logic needs much improvement to achieve better adaptation of regulating the pacing rate to the physiological requirement for each particular patient. In addition, the mathematical complexity in the nonlinear fuzzy control makes the formulation of a tuning mechanism an extremely complex problem.
Therefore, in this paper we propose, for the first time, the combination of input variables with scaling factor of a PID controller and the fuzzy control mechanism for the dual-sensor cardiac pacemaker systems in patients with bradycardias, in which activity and QT interval are employed as adaptive parameters. The Proportional-Integral-Derivative (PID) controller is the most popular control method utilized in the control industry, due to its simplicity, versatility, robustness, and ease of implementtation even for some classes of nonlinear systems [12,13]. Against the conventional fuzzy control scheme, the proposed fuzzy PID (FPID) controller in a closed-loop system determines the optimal pacing rate, automatically regulate the heart rate (HR) to track a desired preset HR profile for each particular patient more accurately and offer an adaptive tuning mechanism.
The ability to track a predetermined heart rate profile is useful in cardiac rehabilitation programs or for safer daily life for individuals with bradycardias. Its application may not only bring more comfort for pacemaker patients, allowing them to be more physically active, but also improve the performance of the medical devices to deal with cardiac diseases.
The rest of this paper is organized as follows. Section II describes the rate regulation with dual-sensors in pacemaker systems. Section III presents the conventional fuzzy control method for pacemaker systems. Section IV illustrates the novel design of an FPID controller for a dual-sensor pacing system and HR regulation. Section V gives case studies of particular patients with the proposed FPID controller. The tracking results in simulation are compared between the proposed one and a conventional fuzzy controller. Finally, the last section presents conclusion and future research directions.
2. Rate Regulation with Dual-Sensors in Cardiac Pacemaker Systems
Pacemakers are used to treat arrhythmias that are problems with the rate or rhythm of heartbeat. They provide electric pulses that mimic the natural pacing system of the heart, maintain an adequate heart rate by delivering controlled, rhythmic electrical stimuli to the chambers of the heart, and prevent human from being harmed by low heart rate [14]. Modern pacemakers with sensors are applied not only for pacing but also for other functions such as obtaining measurements of diagnostic data and providing continuous cardiac monitoring [6].
For seriously and suddenly occurring arrhythmias, especially bradycardias, accurate diagnosis for different conditions of human body, distinguishing between normal and abnormal heartbeats, and maintenance of steady and sufficient heart rate play important roles in the treatment of heart disease. Hence, incorporating physiological information to aid FPID controllers is a signifycant research field for implantable cardiac pacemakers. In the present status of technology, it seems to be very difficult to develop such sensors which would respond to all kinds of physiological demands. It is thus quite logical to combine sensors so that a limitation of one sensor is covered by the others. Therefore, the dual-sensors have been investigated in the recent years.
In order to estimate a patient’s body conditions, e.g., rest or walk, and track all physiological changes well, the most common dual-sensors include association of an accelerometer (activity sensor) giving a rapid response for light or short duration of exercise and a QT interval (metabolic sensor) for measurement of diagnostic data as detailed in [8]. They are adopted to provide activity signal and actual heart rate in our work. During crosscheck both sensors can control each other and the output heart rate is changed only if both or a predominant sensor agrees. For instance, after administration of a drug that shortens the QT interval, a QT interval sensor would indicate the need for rate increase, but the rate would not change because the activity sensor is not triggered. Conversely, passively tapping on the device would activate the activity sensor and indicate a rate increase, but the rate would not be modified because the QT-interval sensor would not be stimulated by such maneuver.
The pacemaker system blends two sensor-rates at a certain percentage to obtain an optimized output rate. The following recommendations are made for a dualsensor rate response:
1) Except as otherwise recommended, the dual-sensor HR (heart rate) output should follow the QT interval indicated rate.
2) At onset of walking, the dual-sensor HR output should follow the accelerometer indicated rate, but only up to 50% of the maximum rate elevation.
3) If the activity response is very low, and the QT interval response [15,16] is very high, limit the dual-sensor rate response to 25% of the maximum rate elevation. This cross-checking prevents long-term pacing at high rates due to hyperventilation in a resting patient.
3. Conventional Control Scheme for Pacemaker Systems
Many physical systems, such as the cardiac pacemaker systems, are either highly nonlinear or too complex to control with traditional strategies. However, if an expert can qualitatively describe a control strategy, one can use fuzzy control to directly translate from the linguistic rules developed by the expert to a rule base for a fuzzy controller [17].
The main idea of fuzzy control systems is to design a controller for a system that is structurally difficult to model due to naturally existing nonlinearities and other modeling complexities [18,19]. Fuzzy control system has the capability of transforming linguistic information and expert knowledge into control signals. It offers a way to map from the verbal requirements to a numerical algorithm, and interpolates smoothly between the specified conditions. The significant and observable variables related to the control actions consist of fuzzy relationship or algorithm. The simplicity of designing these fuzzy systems has been the main advantage of their successful implementation over traditional approaches such as optimal and adaptive control techniques.
Accordingly, the conventional fuzzy control design in the model describes the correlation between the heart rate HR(t) of the patient at time t and the heart rate provided by the pacemaker HRT(t+). The fuzzy rules are formulated as [20].
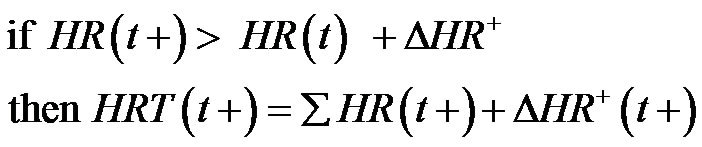 (1)
(1)
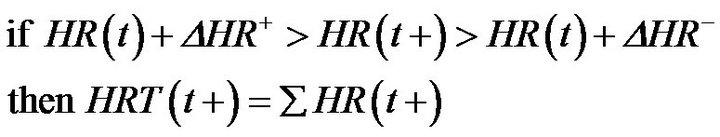 (2)
(2)
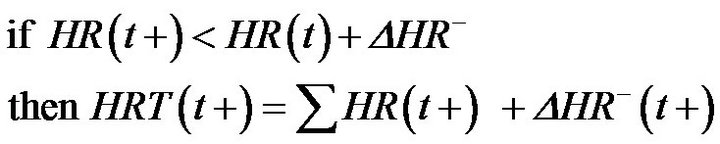 (3)
(3)
 (4)
(4)
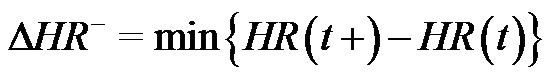 (5)
(5)
where 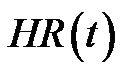 is the desired heart rate of the patient at time t.
is the desired heart rate of the patient at time t.  and
and  limit both the increase and decrease of heart rate, in order to avoid sudden heart rate changes.
limit both the increase and decrease of heart rate, in order to avoid sudden heart rate changes.
The conventional control design cannot exhibit the preciseness of the actual heart rate changing in real-time. It is lack of detailed fuzzy rules to describe the control signal and pacing rate according to diverse cases of the heart rate changing. In addition, the conventional control design was not able to solve the problem of adaptive control for the adjustable pacing rate, which means it could not provide a synchronous tuning mechanism adaptive to the actual heart rate alteration. Therefore, this paper proposes a novel design of controllers for the pacing system by combining fuzzy logic and well-formed formalism of PID control, in order to solve the aforementioned problems and improve the flexibility of the control system for easy personalization.
4. Fuzzy PID Controller for Dual-Sensor Cardiac Pacemaker Systems
4.1. Fuzzy PID Control
The mathematical complexity in the conventional fuzzy control makes the formulation of a tuning mechanism an extremely complex problem [18]. To reduce the complexity of the adaptive tuning system, the linear combination of input variables with a scaling factor of a PID controller adopted in the fuzzy control has been widely applied [21].
Fuzzy controllers have two main parts that need to be designed. One is the control structure composing of fuzzy rules, identifying the fuzzy inputs and outputs and their linguistic description. The other is a fuzzy reasoning method. One of the most widely used design methods for fuzzy controllers is to define membership functions of linguistic variables and to formulate fuzzy rules by control engineers. In fuzzy control, linguistic descriptions of human expertise in controlling a process are represented as fuzzy rules or relations. This knowledge base is used by an inference mechanism, in conjunction with some knowledge of the states of the process in order to determine control actions [22].
For the conventional fuzzy controllers having two in puts and one output, the fuzzy sets of the error e and the change in error ∆e are denoted as Ai1 and Aj2. A fuzzy controller can usually be described by a set of if-then rules.
 (6)
(6)
where u and uij are output control signal and crisp values, respectively. With product-sum inference, the degree of membership of the antecedent part of the rule is
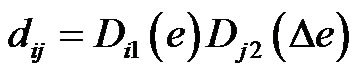 (7)
(7)
where Di1(e) and Dj2(∆e) are the degree of memberships in Ai1 and Aj2.
Due to the PID controller’s simplicity and flexibility, the overall performance with respect to adaptive tuning operations is improved based on conventional fuzzy control. In addition, PID controller adds predictive capability to the controller and improves the transient response so as to reduce error amplitude. It applies a signal to the process that is proportional to the actuating signal in addition to adding integral and derivative of the actuating signal. It consists of three terms reflecting proportional amplification of the error signal, its integration and derivation. Figure 1 shows a conventional PID controller [23] for a system. Its control signal u(t), for a joint variable, x(t), is computed by combining proportional, integral, and derivative terms.
 (8)
(8)
 (9)
(9)
where KP, KI , and KD are the proportional, integral, and derivative gains, respectively.
The cumulative effect of these three components has a main effect for reduction of the steady state behavior due to the integration factor and the improvement of the response speed due to the proportional factor while reduceing response overshoot due to the derivative factor [24,25]. Thus, by taking advantage of both the system of if-then rules in the fuzzy knowledge based system and well-defined PID controller, a novel control design is proposed for the dual-sensor pacing system in this paper. The FPID controller is placed within the feedback con-
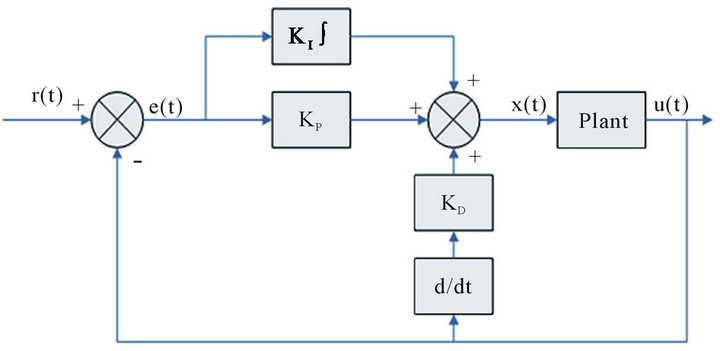
Figure 1. Conventional PID controller.
trol loop, and computes the PID actions through fuzzy inference.
4.2. Design of FPID Controllers
Due to the ambiguity between normal and abnormal estimation especially in medical assessment, fuzzy PID controllers become a good candidate for accurate diagnosis and treatment comparing with the conventional PID controller. For instance, in cases where the difference between normal and abnormal in each of the conditions (e.g., rest or walk) is not clear, such as in early detection of bradycardias, we have to deal with ambiguous information. Consequently, FPID control has the ability to produce better response performances and decrease the propagation of errors against the traditional control schemes for cardiac pacemaker systems [26,27]. Thus, the design of fuzzy PID controllers with dual-sensors adds predictive capability to the controller and improves the transient response so as to reduce error amplitude. In addition, FPID controllers incorporate physiological information and provide more accurate feedback signals, giving a rapid response for light or short duration of exercise and a QT interval for measurement of diagnostic data as detailed in [8]. In order to decrease the propagation of errors, during crosscheck both sensors can control each other and the output heart rate is changed only if both or a predominant sensor agrees. For instance, after administration of a drug that shortens the QT interval, a QT interval sensor would indicate the need for rate increase, but the rate would not change because the activity sensor is not triggered.
Dual-sensor cardiac pacemakers will become more and more sophisticated with the progress of electrophysiological and hemodynamic understanding of the heart as well as hardware/software technologies such as sensors and microprocessors. Such a pacing system requires more flexible and powerful controller that has ability to be upgraded with the same hardware. Fuzzy PID controllers are such a promising candidate for the control algorithm in a pacemaker.
There are different types of fuzzy PID controllers [28,29]. One of the earliest and very effective structures uses a two-dimensional linear rule base with standard triangular membership functions [30], which combines fuzzy PI and fuzzy PD controllers. For classical PID controllers, the control action is determined by performing arithmetic operations on error inputs. For fuzzy control part, one may have to consider the algebraic operations for fuzzy quantities [31]. The fuzzy PID controller designed in our work is cascaded to the plant, I.e., human heart, as shown in Figure 2, in which there are three inputs for each fuzzy processing block (fuzzy channel), FC1-FC3, in which FC denotes fuzzy channel. A fuzzy channel is a block where fuzzy reasoning is used. The
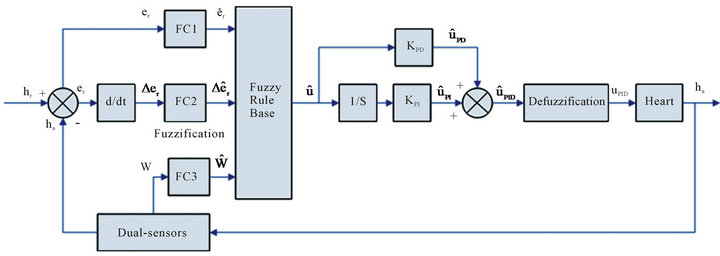
Figure 2. Design of fuzzy PID controller for dual-sensors cardiac pacemaker system.
corresponding normal heart rate recorded for each particular patient during rest and walk is applied as the preset/desired profile or reference signal, while actual heart rate is measured in accordance with the dual-sensor rate response recommendations stated earlier.
In Figure 2, denote the preset heart rate as the reference input hr; the output, actual heart rate, measured by dual-sensors as ha; and the error between hr and ha as er. The heart rate error er, change of error Δer and activity signal w are processed in the input fuzzy channels FC1- FC3. Each channel produces its output êr, Δêr and ŵ. The fuzzification module converts the inputs into members of fuzzy sets, in order to make them compatible with the fuzzy set representations in the rule base. It is performed by comparing numeric values of the HR error and the change of HR error against certain thresholds and assigning appropriate linguistic values to them. The error input provides the nonlinear proportional actions through fuzzy inference. After the fuzzy PI and fuzzy PD controllers, the defuzzified control signal uPID, which is actually the pacing rate adjustable by the FPID controller and applied to the heart, is obtained.
4.3. FPID Control Rules and Membership Functions
The fuzzy set of bradycardias is very strict in the sense that it cannot exhibit the impreciseness of the concept that is felt if hesitating to classify an instance with the actual heart rate not exactly but nearing 60 bpm as a very clear case of bradycardias. In order to accommodate this fine imprecision of the heart rate error and the change of error, fuzzy rules should be allowed to vary smoothly by adding linguistic variables. Linguistic descriptions of human expertise in controlling a process are represented as fuzzy rules. This knowledge base is used by an inference mechanism, in conjunction with some knowledge of the process states in order to determine control actions. The fuzzy rule bases for the heart rate interpretation are defined using linear rules to form a fuzzy production system that uses generalized modus ponens (GMP) [32,33]. GMP is a categorical inference rule, offered by fuzzy logic—to perform approximation in drawing inferences when the existing rule base is found to be incomeplete and inexact in respect to finer variations of actual heart rate from the feedback. Most patients with bradycardias achieve normal heart rates of 70 to 95 bpm, 85 to 90 bpm with a casual walk and 100 to 110 bpm with a brisk walk [34]. In order to take care of finer variations in the heart rate patterns, the proposed system equipped with GMP can perform qualified diagnosis as follows. Here, for instance, an average heart rate of 82.5 to 107.5 bpm at rest is expressed in the form of LH for “a little high”, VH for “very high”, and EH for “extremely high”. Therefore, we use 9 linguistic variables.
The nonlinearity in the control signal is achieved by changing the variables associated with membership functions. For activity signal, fuzzy set w for a patient at rest is assigned a membership value 0 based on the detection result of dual-sensors, and for light exercise or walk assigned a membership value 1. So the membership function, denoted by μw for the fuzzy set w, can have either 0 or 1 value for any element of its domain of discourse, expressed as μw Î {0, 1}. Using these variables, several control rules are described as follows. A number of such rules covering all possible signal levels are formulated. The fuzzy rule bases of the FPID system are illustrated in Table 1 [35,36]. The meaning of the linguistic variables is explained in Table 2.
Several examples of the fuzzy rules in Table 1 are as follows:
 (10)
(10)
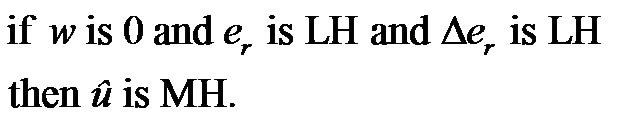 (11)
(11)
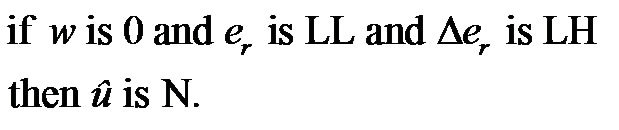 (12)
(12)
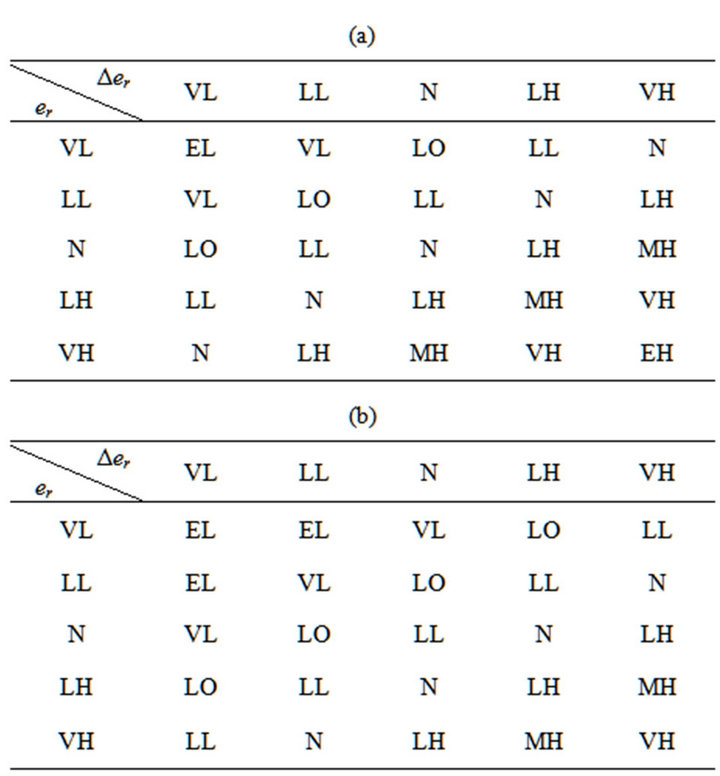
Table 1. Fuzzy rule bases of the fpid system. (a) w = 0; (b) w = 0.
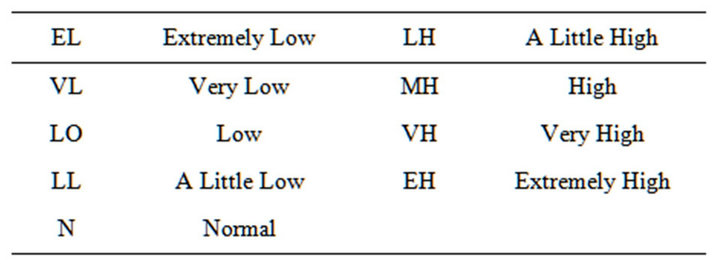
Table 2. Meanting of the linguistic variables.
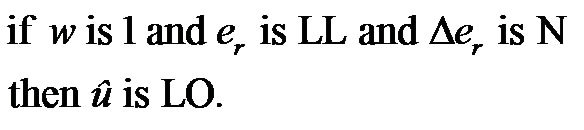 (13)
(13)
 (14)
(14)
 (15)
(15)
where û is the corresponding fuzzy pacing rate after the fuzzification. The linguistic variables for fuzzy rate output indicate the intensity of the stimuli with adjustable pacing rate generated by the pacemaker.
Membership functions that cover the interior of the input space have the triangular shapes, with the exception of the membership functions on both ends of the input which are trapezoidal. Membership functions used in the calculation of fuzzy pacing rate are isosceles triangles with the same bases as shown in Figure 3. They are used to map from an input variable to a fuzzy variable and from a fuzzy variable to an output variable. Furthermore, assuming that only the neighboring fuzzy variables can
 (a)
(a)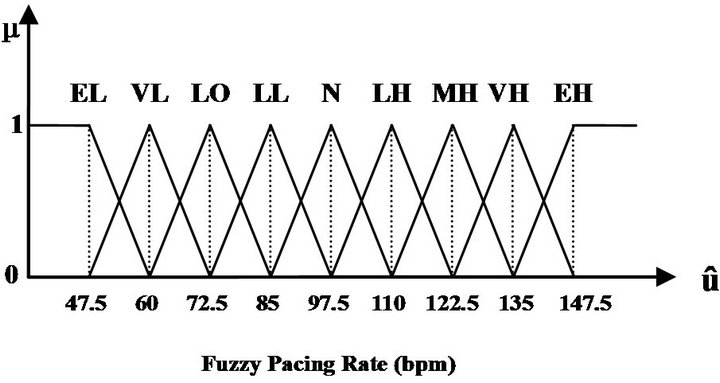 (b)
(b)
Figure 3. Membership functions. (a) Membership functions of fuzzy pacing rate at rest (w = 0); (b) Membership functions of fuzzy pacing rate during walk (w = 1).
intersect and the following condition is satisfied:
 (16)
(16)
The composed fuzzy PI and PD actions for determineing the fuzzy PID pacing rate are given by
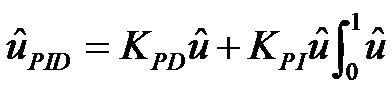 (17)
(17)
In addition to the above, the fuzzy PID pacing rate is then defuzzified using the standard center of area (COA) method [37] yielding the subsequent pacing rate provided by the pacemaker and applied on the heart corresponding to the current actual heart rate.
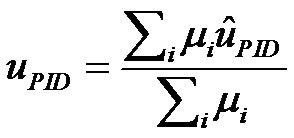 (18)
(18)
In the case of rest, for instance, if the actual heart rate measured by dual-sensors is lower than preset normal rate for the particular patient, in order to assist the heartbeat to be regular, the stimuli with adjustable pacing rate are generated by the pacemaker according to the FPID controller, such that the actual heart rate may track the preset desired heart rate in real-time.
5. Case Studies and Simulation Results
Closed-loop control of biological systems permits tight regulation and instantaneous determination of the physicological state or response for automated computer-mediated interaction with cardiac tissues [38]. The FPID control system described in this paper achieves the closedloop control of a cardiac cell and the system parameters of controlling variables to determine the pacing rate and achieve the desired response.
In designing a control system, the second step is to obtain a mathematical model of the plant for the controller. In order to demonstrate the feasibility of the proposed FPID controller for a pacing system and for consistency with our previous work [8,39], we implement the case studies by adopting medical data sets of particular patients for simulation on the heart model—YNI model (Yanagihara, Noma, and Irisawa) [40]. It is the mathematical model of the plant for simulating heart activities. The YNI model exhibits the potential behavior of a heart, as a proven cardiac sinoatrial node model. The tracking results are given in this section.
The preset heart rate profile may be obtained using the data from the same patient while recorded in a normal state or, if not possible, from the normal subjects of almost the same age and performing the similar daily activities, or the data from other patients of the same pathological background.
In our proposed FPID based cardiac pacemaker system, the patient’s heart performance is then simulated using the medical data sets, as the preset/desired heart rate profile, from [41-43] based on the YNI heart model. Table 3 presents the characteristics of individual patients and the corresponding preset HR during rest and walk. We utilize the proposed FPID controller and conventional fuzzy control algorithm [20], respectively, to determine the pacing rate of a pacemaker.
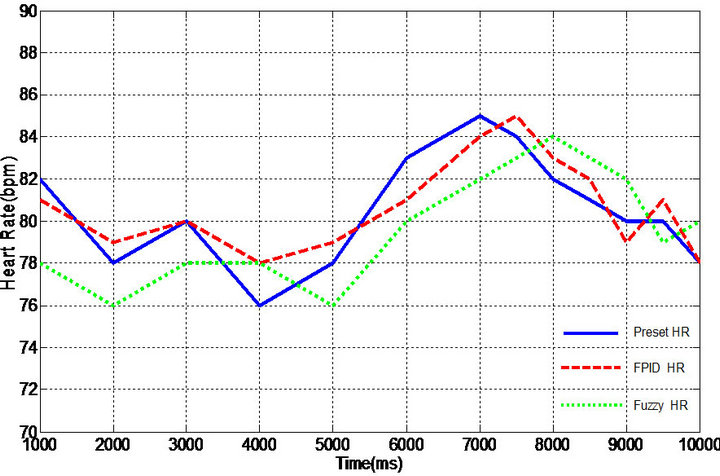
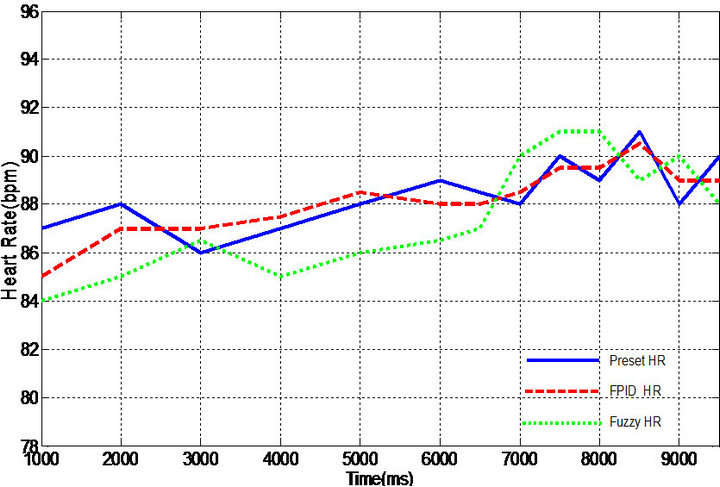
The tracking performances of FPID controlled actual HR and fuzzy controlled HR to the preset HR are compared in Figures 4-5 for the particular patients with bradycardias at rest and walk, respectively. The overall tracking and agreement of the rates with FPID is more effective for heartbeat recovery and maintenance than conventional fuzzy control approach. Cardiac abnormalities such as bradycardia are a major cause of morbidity and mortality. Early diagnosis and medical treatment of heart diseases can prevent the sudden death of a patient. Thus, in order to provide rapid response, the first 10- second is the most important part to show and compare
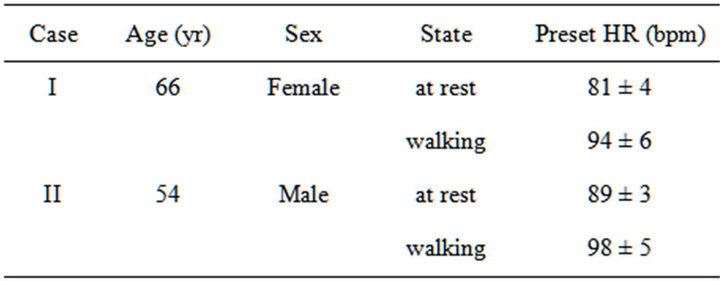
Table 3. Individual characteristics of particular patients.
 (a)
(a)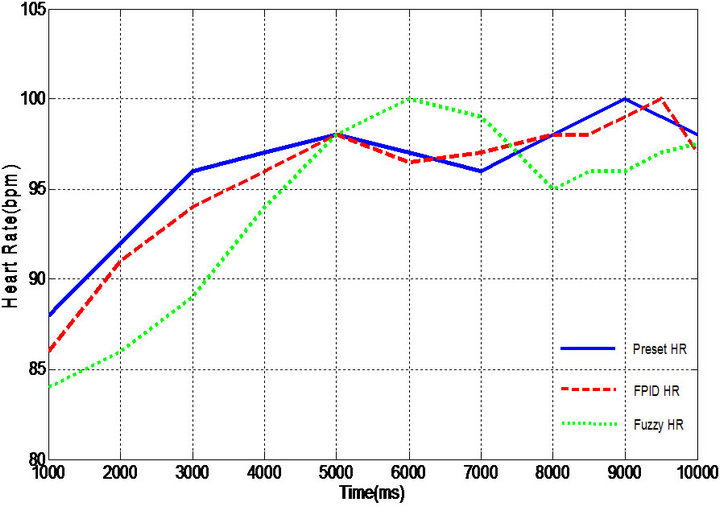 (b)
(b)
Figure 4. Heart rate tracking for case I. (a) At rest; (b) While walking.
the performance of the controllers.
The comparison of simulation results between proposed FPID controller and conventional fuzzy algorithm is demonstrated in Table 4, including the root-meansquare error (rmse) and the maximum error percent. Quite satisfactory tracking of the desired heart rate profile achieved with the FPID controller exhibits that the novel control design decreases rmse and maximum error, increases the accuracy of tracking, and improves the real-time adaptation of heart rate variation. From the results, an FPID pacing system is more stable while tracking the preset HR in comparison of conventional fuzzy control algorithm [20]. Especially when the patient is taking a walk, the conventional fuzzy control is not able to achieve synchronously the physiological demands in body state change.
To accommodate the fine imprecision of the heart rate, the proposed fuzzy rules are set to be allowed for smooth variation by adding sufficient linguistic variables. Also, by tuning the parameters of the PID controller flexibly and easily, it may achieve an optimal pacing rate of pacemakers. Thus, the proposed method is proved to be very promising for heart rate control in a dual-sensor pacing system.
 (a)
(a)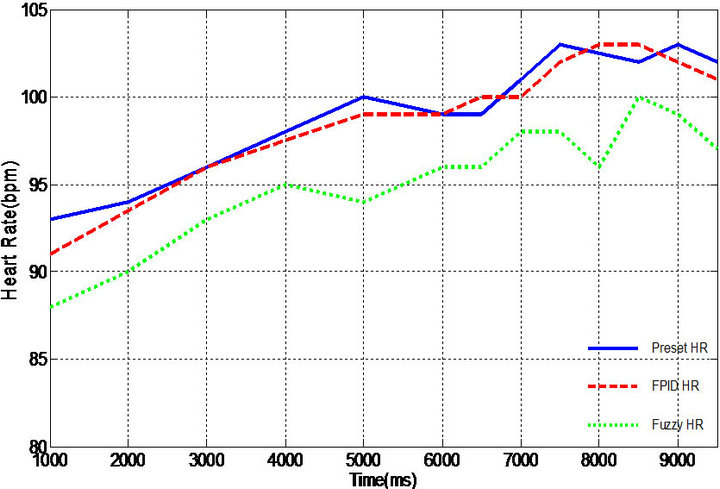 (b)
(b)
Figure 5. Heart rate tracking for case II. (a) At rest; (b) While walking.
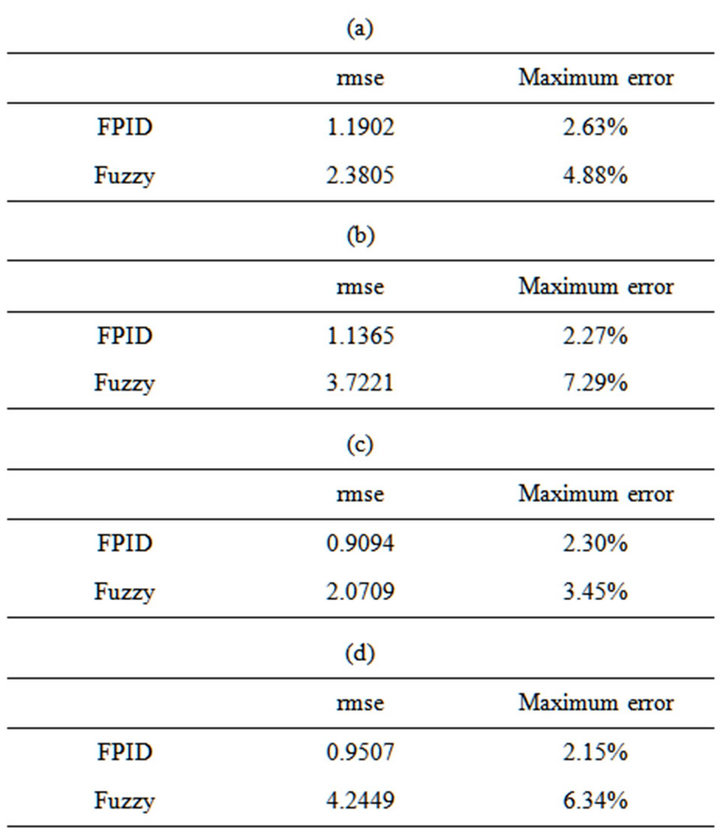
Table 4. Comparison of simulation results between proposed novel FPID controller and conventional fuzzy control algorithm. (a) Case I—Resting; (b) Case I—Walking; (c) Case II—Resting; (d) Case II—Walking.
Physicians can readjust the control rules intuitively by their own language and this offers the possibility to realize more versatile pacing system with multiple indicators. Simultaneous monitoring of several sensor signals is beneficial for additional functions which can be also realized more easily and flexibly by the FPID.
6. Conclusion and Future Work
In this paper, we design a fuzzy PID controller for the heart rate control based on dual-sensor (accelerometer and QT interval) pacemaker systems and demonstrate its feasibility and efficiency of automated rate regulation. Through comparing with the conventional fuzzy control algorithm, fuzzy PID provides a more suitable control strategy to determine a pacing rate in order to achieve a closer match between actual heart rate and a desired profile in the cases of rest and walk. It is more effective for heartbeat recovery, maintenance and real-time cardiac monitoring. Satisfactory heart rate tracking results with FPID are achieved by using an individual patient’s medical data sets. Our future work will deal with the problems with a sudden increase and decrease of activity covering other states of human body.
REFERENCES
- E. Kenneth, A. U. Rajendra, N. Kannathal and L. C. Min, “Data Fusion of Multimodal Cardiovascular Signals,” Proceedings of 27th Annual International Conference of the IEEE Engineering in Medicine and Biology, Shanghai, 2005, pp. 4689-4692.
- M. Sthlberg, R. Kessels, C. Linde and F. Braunschweig, “Acute Haemodynamic Effects of Increase in Paced Heart Rate in Heart Failure Patients Recorded with an Implantable Haemodynamic Monitor,” Europace, Vol. 13, No. 2, 2011, pp. 237-243. doi:10.1093/europace/euq354
- X. Liu, Y. Zheng, M. W. Phyu, B. Zhao, M. Je and X. Yuan, “Multiple Functional ECG Signal Is Processing for Wearable Applications of Long-Term Cardiac Monitoring,” IEEE Transactions on Biomedical Engineering, Vol. 58, No. 2, 2011, pp. 380-389. doi:10.1109/TBME.2010.2061230
- D. J. Woollons, “To Beat or not to Beat: The History and Development of Heart Pacemakers,” Engineering Science and Education Journal, Vol. 4, No. 6, 1995, pp. 259-268. doi:10.1049/esej:19950604
- S. A. P. Haddad, R. P. M. Houben, and W. A. Serdijin, “The Evolution of Pacemakers,” IEEE Engineering in Medicine and Biology Magazine, Vol. 25, No. 3, 2006, pp. 38-48. doi:10.1109/MEMB.2006.1636350
- R. K. Shepard and K. A. Ellenbogen, “Leads and Longevity: How Long Will Your Pacemaker Last?” Europace, Vol. 11, No. 2, 2009, pp. 142-143. doi:10.1093/europace/eun359
- M. K. Das, G. Dandamudi, and H. A. Steiner, “Modern Pacemakers: Hope or Hype,” Pacing and Clinical Electrophysiology, Vol. 32, No. 9, 2009, pp. 1207-1221. doi:10.1111/j.1540-8159.2009.02467.x
- W. V. Shi and M. C. Zhou, “Recent Advances of Sensors for Pacemakers,” Proceeding of 2011 IEEE International Conference on Networking, Sensing and Control, Delft, 11-13 April 2011, pp. 520-525. doi:10.1109/ICNSC.2011.5874939
- A. Arnaud and C. Galup-Montoro, “Fully Integrated Signal Conditioning of an Accelerometer for Implantable Pacemakers,” Analog Integrated Circuits and Signal Processing, Vol. 49, No. 3, 2006, pp. 313-321. doi:10.1007/s10470-006-9708-y
- P. L. Johnson, J. C. Newton, D. L. Rollins, W. M. Smith and R. E. Ideker, “Adaptive Pacing during Ventricular Fibrillation,” Pacing and Clinical Electrophysiology, Vol. 26, No. 9, 2003, pp. 1824-1836. doi:10.1046/j.1460-9592.2003.t01-1-00276.x
- W. K. Wong, E. Bai and A. W. C. Chu, “Adaptive TimeVariant Models for Fuzzy-Time-Series Forecasting,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 40, No. 6, 2010, pp. 1531-1542. doi:10.1109/TSMCB.2010.2042055
- M. H. Hung, L. S. Shu, S. J. Ho, S. F. Hwang and S. Y. Ho, “A Novel Intelligent Multiobjective Simulated Annealing Algorithm for Designing Robust PID Controllers,” IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, Vol. 38, No. 2, 2008, pp. 319-330. doi:10.1109/TSMCA.2007.914793
- F. Karray, W. Gueaieb and S. Al-Sharhan, “The Hierarchical Expert Tuning of PID Controllers Using Tools of Soft Computing,” Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 32, No. 1, 2002, pp. 77-90. doi:10.1109/3477.979962
- S. Petrutiu, A. V. Sahakian, A. Ricke, B. Young and S. Swiryn, “High Resolution Electrocardiography Optimized for Recording Pulses from Electronic Pacemakers: Evaluation of a New Pacemaker Sensing System,” Computers in Cardiology, Durham, NC, 30 September-3 October 2007, pp. 197-200.
- P. Kligfield, K. G. Lax and P. M. Okin, “QT IntervalHeart Rate Relation during Exercise in Normal Men and Women: Definition by Linear Regression Analysis,” Journal of the American College of Cardiology, Vol. 28, No. 6, 1996, pp. 1547-1555. doi:10.1016/S0735-1097(96)00351-8
- G. F. Mitchell, A. Jeron and G. Koren, “Measurement of Heart Rate and QT Interval in the Conscious Mouse,” American Journal of Physiology-Heart and Circulatory Physiology, Vol. 274, No. 3, 1998, pp. H747-H751.
- C. W. Tao, “A Reduction Approach for Fuzzy Rule Bases of Fuzzy Controllers,” Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 32, No. 5, 2002, pp. 668-675. doi:10.1109/TSMCB.2002.1033186
- K. C. Sio and C. K. Lee, “Stability of Fuzzy PID Controllers,” IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, Vol. 28, No. 4, 1998, pp. 490-495. doi:10.1109/3468.686710
- L. X. Wang and J. M. Mendel, “Generating Fuzzy Rules by Learning from Examples,” IEEE Transactions on Systems, Man and Cybernetics, Vol. 22, No. 6, 1992, pp. 1414-1427. doi:10.1109/21.199466
- A. Wojtasik, Z. Jaworski, W. Kuzmicz, A. Wielgus, A. Walkanis and D. Sarna, “Fuzzy Logic Controller for Rate-Adaptive Heart Pacemaker,” Applied Soft Computing Journal, Vol. 4, No. 3, 2004, pp. 259-270. doi:10.1016/j.asoc.2004.03.005
- C. W. Tao and J. S. Taur, “Flexible Complexity Reduced PID-Like Fuzzy Controllers,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 30, No. 4, 2000, pp. 510-516. doi:10.1109/3477.865168
- Z. Y. Zhao, M. Tomizuka and S. Isaka, “Fuzzy Gain Scheduling of PID Controllers,” IEEE Transactions on Systems, Man and Cybernetics, Vol. 23, No. 5, 1993, pp. 1392-1398. doi:10.1109/21.260670
- W. Li, X. G. Chang, J. Farrell and F. M. Wahl, “Design of an Enhanced Hybrid FUZZY P+ID Controller for a Mechanical Manipulator,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 31, No. , 2001, pp.938-945. doi:10.1109/3477.969497
- J. G. Juang, M. T. Huang and W. K. Liu, “PID Control Using Presearched Genetic Algorithms for a MIMO System,” IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, Vol. 38, No. 5, 2008, pp. 716-727.
- A. Odwyer, “Handbook of PI and PID Controller Tuning Rules,” Imperial College Press, London, UK, 2003. doi:10.1142/p277
- E. Harinath and G. K. I. Mann, “Design and Tuning of Standard Additive Model Based Fuzzy PID Controllers for Multivariable Process Systems,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 38, No. 3, 2008, pp. 667-674. doi:10.1109/TSMCB.2008.919232
- M. Margaliot and G. Langholz, “Hyperbolic Optimal Control and Fuzzy Control,” IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, Vol. 29, No. 1, 1999, pp. 1-10. doi:10.1109/3468.736356
- H. X. Li, L. Zhang, K. Y. Cai and G. Chen, “An Improved Robust Fuzzy-PID Controller with Optimal Fuzzy Reasoning,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 35, No. 6, 2005, pp. 1283-1294. doi:10.1109/TSMCB.2005.851538
- G. K. I. Mann, B. G. Hu and R. G. Gosine, “Analysis of Direct Action Fuzzy PID Controller Structures,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 29, No. 3, 1999, pp. 371-388. doi:10.1109/3477.764871
- H. X. Li and H. B. Gatland, “Conventional Fuzzy Control and its Enhancement,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 26, No. 5, 1996, pp. 791-797. doi:10.1109/3477.537321
- G. K. I. Mann, B. G. Hu and R. G. Gosine, “Two-Level Tuning of Fuzzy PID Controllers,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 31, No. 2, 2001, pp. 263-269. doi:10.1109/3477.915351
- A. G. Hatzimichailidis and B. K. Papadopoulos, “Ordering Relation of Fuzzy Implications,” Journal of Intelligent and Fuzzy Systems, Vol. 19, No. 3, 2008, pp. 189-195.
- Y. Tsukamoto, “A Normative Approach to Fuzzy Logic Reasoning Using Residual Implications,” Journal of Advanced Computational Intelligence and Intelligent Informatics, Vol. 13, No. 3, 2009, pp. 262-267.
- D. L. Hayes, P. A. Friedman and M. Lloyd, “Cardiac Pacing and Defibrillation: A Clinical Approach,” WileyBlackwell, 2000.
- H. Wang, Y. Rong and T. Wang, “Laminar Cooling Control Based on Fuzzy-PID Controller,” IEEE International Conference on Information Management and Engineering, Chengdu, 16-18 April 2010, pp. 7-10.
- A. Visioli, “Fuzzy Logic Based Set-Point Weight Tuning of PID Controllers,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 29, No. 6, 1999, pp. 587-592. doi:10.1109/3468.798062
- B. M. Mohan and A. V. Patel, “Analytical Structures and Analysis of the Simplest Fuzzy PD Controllers,” IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 32, No. 2, 2002, pp. 239-248. doi:10.1109/3477.990881
- R. H. Whittington, L. Giovangrandi and G. T. A. Kovacs, “A Closed-Loop Electrical Stimulation System for Cardiac Cell Cultures,” IEEE Transactions on Biomedical Engineering, Vol. 52, No. 7, 2005, pp. 1261-1270. doi:10.1109/TBME.2005.847539
- W. V. Shi, T. N. Chang and M. C. Zhou, “Method to Detect Cardiac Abnormalities Based on Electrocardiography and Sinoatrial Pacemaker Model,” Proceedings of IEEE International Conference on Mechatronics and Automation, Xi’an, 4-7 August 2010, pp. 566-571.
- J. Keener and J. Sneyd, “Mathematical Physiology,” Springer, New York, 1998.
- V. Aboyans, M. Frank, K. Nubret, P. Lacroix and M. Laskar, “Heart Rate and Pulse Pressure at Rest Are Major Prognostic Markers of Early Postoperative Complications after Coronary Bypass Surgery,” European Journal of Cardio-Thoracic Surgery, Vol. 33, No. 6, 2008, pp. 971- 976. doi:10.1016/j.ejcts.2008.01.065
- A. D. Blaufox, L. A. Sleeper, D. J. Bradley, R. E. Breitbart, A. Hordof, R. J. Kanter, E. A. Stephenson, M. Stylianou, V. L. Vetter and J. P. Saul, “Functional Status, Heart Rate, and Rhythm Abnormalities in 521 Fontan Patients 6 to 18 Years of Age,” Journal of Thoracic and Cardiovascular Surgery, Vol. 136, No. 1, 2008, pp. 100- 107. doi:10.1016/j.jtcvs.2007.12.024
- A. Ferro, C. Duilio, M. Santomauro and A. Cuocolo, “Walk Test at Increased Levels of Heart Rate in Patients with Dual-Chamber Pacemaker and with Normal or Depressed Left Ventricular Function,” European Heart Journal, Vol. 24, No. 23, 2003, pp. 2123-2132. doi:10.1016/j.ehj.2003.09.007

