Advances in Breast Cancer Research
Vol.06 No.01(2017), Article ID:73056,15 pages
10.4236/abcr.2017.61001
Survival Analysis for a Breast Cancer Data Set
Hong Li
Department of Mathematical Sciences, Cameron University, Lawton, OK, USA

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 29, 2016; Accepted: December 25, 2016; Published: December 28, 2016
ABSTRACT
A survival analysis on a data set of 295 early breast cancer patients is performed in this study. A new proportional hazards model, hypertabastic model was applied in the survival analysis. We assume a proportional hazards model, and select two sets of risk factors for death and metastasis for breast cancer patients respectively by using standard variable selection methods. To evaluate the performance of the new model and compare it with other popular distributions, Cox, Weibull and log-logistic models were fitted to the data besides the hypertabastic model. Result shows that the hypertabastic proportional hazards model outperformed all the comparison models and provided the best fit for the breast cancer data. In addition, we observed that the gene expression variable, wound response signature, combined with other clinical variables, can provide an effective model to predict the overall survival and hazard rate for breast cancer patients.
Keywords:
Proportional Hazards Model, Hypertabastic Model, Survival Function, Hazard Function, Log-Likelihood

1. Introduction
Time to event models, commonly known as survival or reliability model, have been studied and applied in a variety of scientific disciplines such as medicine, biology, engineering and business. Cox proportional hazards model is one of the most commonly used nonparametric/semiparametric models; it does not require any specific assumption about the shape of survival function. However, it usually does not provide a very good fit to the data through the simulation studies. On the other hand, if the assumption for parametric distribution is met for the data under consideration, it will be more efficient and easier to interpret estimates than nonparametric/semiparametric models. Some well established parametric models, such as Weibull, log-normal and log-logistic model have been widely used to model the time to event data in many applications. The Hosmer and Lemeshow [1] , Klein and Moeschberger [2] , and Therneau and Grambsch [3] gave an overview of survival data modeling techniques. Foulkes et al. [4] used several parametric models to access the prognostic factors in the recurrence of ischemic strokes. Kannan et al. [5] used log-logistic probability distribution to model altitude decompression sickness risk and symptom onset time. Sama et al. [6] used five parametric models to analyze the survival time data of Plasmodium falciparum infections and found that the best fit could be obtained from a parametric model―Weibull distribution. In this article, a new parametric model― hypertabastic survival model is briefly reviewed in Section 2. To compare the performance of these models, a breast cancer data with 295 patients from the Netherlands Cancer Institute was studied. This data had previously been used to identify and validate a prognostic gene expression profile. It also had been used to test the reproducibility of the association between the wound-response signature and breast cancer progression. The authors studied two events, death due to breast cancer and metastasis (spread of breast cancer) separately in this article. A data description and analysis methods are given in Section 3. Variable selection and results for model comparisons are discussed in detail in Section 4. The main results for metastasis are given in Section 5. A discussion is given in Section 6.
2. Hypertabastic Proportional Hazards Model
Tabatabai et al. [7] proposed a new probability distribution, hypertabastic distribution, and hypertabastic survival model. Let T be a continuous random variable representing the waiting time until the occurrence of an event. The hypertabastic baseline survival function is defined by
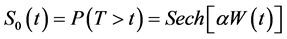 (1)
(1)
where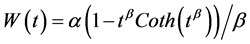 ,
, 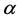 and
and 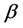 are the model parameters and both positive. Correspondingly, the hypertabastic baseline hazard function is given by
are the model parameters and both positive. Correspondingly, the hypertabastic baseline hazard function is given by
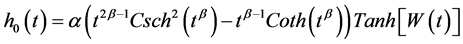 (2)
(2)
With the change of the value of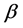 , the baseline hazard function can have more flexible form compared to other parametric models. Under the proportional hazards assumption, they introduced the hypertabastic proportional hazards model. The hazard function for this model is given by
, the baseline hazard function can have more flexible form compared to other parametric models. Under the proportional hazards assumption, they introduced the hypertabastic proportional hazards model. The hazard function for this model is given by
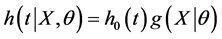 (3)
(3)
where 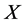 is a p-dimensional vectors of covariates,
is a p-dimensional vectors of covariates, 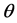 is a vector of unknown parameters,
is a vector of unknown parameters, 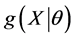 is non negative function of
is non negative function of 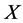 satisfying the condition that
satisfying the condition that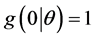 , and
, and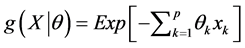 . Similarly, the hypertabastic survival function for this model is defined by
. Similarly, the hypertabastic survival function for this model is defined by
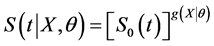 (4)
(4)
Then, the hypertabastic probability density function for the proportional hazards model is given by
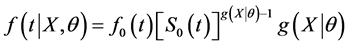 (5)
(5)
where 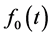 is the baseline density function and defined as
is the baseline density function and defined as
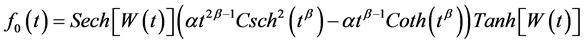 (6)
(6)
All the unknown parameters, including  and
and
where
For further details, see [7] .
3. Data Description and Analysis Methods
The breast cancer data includes a series of 295 consecutive women with breast cancer who were treated at the hospital of the Netherlands Cancer Institute. All 295 patients’ age at diagnosis was 52 years or younger. The calendar year of diagnosis was between 1984 and 1995. Van et al. [8] used the data as a validation set for the seventy gene signature (70G). Tabatabai et al. [9] studied the effect of 70G, core serum response signature correlation (CSR) and ErbB2+ correlation (CERBB) on survival using the hypertabastic model. Chang et al. [10] identified a set of “core serum response” (CSR) genes. In their study, 295 tumor samples were grouped by similarity of the expression pattern of the CSR genes by using hierarchical clustering. The samples were segregated into two classes, activated vs. quiescent by the predominant expression of the serum-induced and serum repressed CSR genes.
The data was censored on the date of the last follow up visit, death from causes other than breast cancer, etc. All the 295 patients had stage I and II breast cancer but had no previous history of cancer. The main clinical variables we studied are age of patient, diameter of tumor, number of positive lymph nodes, tumor grade (3 levels: grade 1, well differentiated; grade 2, moderately differentiated; grade 3, poorly differentiated), estrogen receptor status (ER, two levels: positive and negative), chemo therapy status (two levels: with and without chemo therapy). In general, grade 1 tumors resemble normal cells, and tend to grow and multiply slowly. Grade 1 tumors are generally considered the least aggressive in behavior. Grade 3 tumors tend to grow rapidly and spread faster than tumors with a lower grade. A score of estrogen receptor positive (ER+) means that estrogen is causing the tumor to grow, and that the cancer should respond well to hormone suppression treatments. If the score is estrogen receptor negative (ER−), then the tumor is not driven by estrogen, and the results will need to be evaluated along with other tests.
The primary gene expression variable considered in this study is wound response gene expression signature (WRS, two levels: activated and quiescent). Wound response signature has been found in different studies that it predicted the poor overall survival and increased risk of metastasis [10] [11] .
The proportional hazards assumption was examined first in this study. Four survival models including Cox, Weibull, log-logistic, and hypertabastic models were applied to the breast cancer data and survival analysis for both death due to breast cancer and metastasis were performed. Models were compared by using standard measures of goodness of fit. SAS 9.3 was used for all the model fittings and graphs.
When the effect of risk factors is to change the baseline hazard function by a proportionate amount over the survival time, a proportional hazards model is usually assumed. In Chang et al. [10] , Cox proportional hazards model was fitted to the data. Figure 1 gives the Kaplan-Meier (KM) survival curves for both time to death and time to metastasis. To further assess the proportion hazards (PH) assumption, the log-log KM survival curves for each of the variables was examined. The graphs should result in parallel curves if the assumption is met. Figure 2 gives the plots for WRS and tumor grade when the time to death is modeled. Figure 3 shows the graphs for WRS and tumor grade when the time to metastasis is modeled. Although the curves are not parallel on some time intervals, no apparent interactions between curves showed on the graphs. They indicate that the proportional hazards assumption is satisfied for these variables for both events.
4. Variable Selection and Model Comparisons
To study the time to death due to breast cancer, a set of significant risk factors (predictor variables) for death was selected first. Using the stepwise and forward selection methods outlined in Hosmer and Lemeshow [1] [12] , Cox proportional hazards model was fitted to the data first and identified a set of significant risk factors that are given in Table 1. Next, the hypertabastic proportional hazards model was also fitted to the data using forward selection method and partial likelihood ratio test, it identified the same set of risk factors as the Cox model except the diameter. Since diameter is selected by the Cox model, it was included in each comparison model. In addition, the possibility of interactions among variables is also considered. The significance of each interaction is assessed by adding it to the main effect model and using the partial likelihood ratio test, no significant interactions were identified by the selection process.
Parametric models, such as Weibull and log-logistic models have been widely applied for survival analysis. To study the risk factors for death due to breast cancer and compare the performance of different models, Cox, Weibull, log-lo- gistic and hypertabastic model were fitted to the data set assuming proportional


Figure 1. (a) Kaplan-Meier survival curve (time to death); (b) Kaplan-Meier survival curve (time to metastasis).


Figure 2. (a) Plot of log(−log(S)) vs. log of time stratified by WRS; (b) Plot of log(−log(S)) vs. log of time stratified by tumor grade (time to death).


Figure 3. (a) Plot of log(−log(S)) vs. log of time stratified by WRS; (b) Plot of log(−log(S)) vs. log of time stratified by tumor grade (time to metastasis).
Table 1. Analysis of risk factors for death for four comparison models
WRS represents wound response signature, activated vs. quiescent; ER represents estrogen receptor status, positive vs. negative.
hazards. Models were compared by using log-likelihood value (Log L), Akaike Information Criterion (AIC), and Bayesian Information Criterion (BIC) which assess the goodness of fit of the models. The model with the lowest AIC or BIC corresponds to the best fit model and is preferred. The result including parameter estimates, p-value and hazard ratio for each model is given in Table 1. It shows that the log-likelihood is the highest for the hypertabastic model, AIC and BIC statistics are the lowest for the hypertabastic model when fitted to the breast cancer data. This indicates that the hypertabastic proportional hazards model fits the breast cancer data best.
Among all the variables included in the model, WRS (Wound response gene expression signature) is clearly the most significant with the smallest p-value and a hazard ratio around 2. Age of patients, ER status and tumor grade have relatively small p-values and hazard ratios below or above 1. They are considered as significant (at significance level of 0.05) based on the hypertabastic model. The mean age of patients is 44 years, and the mean tumor diameter is 22.54 mm. Based on the hypertabastic proportional hazards model, holding age and diameter at mean level, we computed the median survival time for some combinations of different levels of other risk factors. The result is given in Table 2. Figure 4 gives the graphs of the hypertabastic baseline survival and hazard functions for this data. Holding age and diameter at mean level and ER score positive, Figure 5 gives the graphs of the hypertabastic survival and hazard functions at different types of wound response signature when tumor grade is poorly differentiated. Similarly, Figure 6 gives the graphs of the hypertabastic survival and hazard functions at different levels of tumor grade when wound response signature is
Table 2. Median survival time at mean age and mean diameter.

Figure 4. (a) Hypertabastic baseline survival function; (b) Hypertabastic baseline hazard function (time to death).


Figure 5. (a) Hypertabastic survival function stratified by WRS; (b) Hypertabastic hazard function stratified by WRS (time to death).


Figure 6. (a) Hypertabastic survival function stratified by tumor grade; (b) Hypertabastic hazard function stratified by tumor grade (time to death).
activated. They indicate that patients with activated wound response signature have about half the median survival time compared to those with quiescent wound response signature when other factors are held constant. Similarly, holding other factors constant, patients with a ER score positive have twice the median survival time as those with a ER score negative.
5. Results for Metastasis
Followed the similar procedure as in the study of time to death and assumed proportional hazards, four comparison models, Cox, Weibull, log-logistic and hypertabastic model were fitted to the breast cancer data. The estimates of parameters, p-value, and hazard ratio for each variable are given in Table 3. The significant risk factors for metastasis were found to be patient’s age, diameter of tumor, number of positive lymph nodes, tumor grade, wound response signature and chemo therapy status. No significant interactions among variables were identified. The result again shows that the AIC and BIC statistics are the smallest for the hypertabastic model. It indicates that the hypertabastic proportional hazards model fits the data best when the interested survival time associated with metastasis.
The mean positive lymph nodes number is 1.4 for this data. Based on the hypertabastic proportional hazards model, the relative risk for a breast cancer patient without chemotherapy compared to a patient with chemotherapy is 1.54 holding other factors constant. At mean level of age, diameter and lymph nodes number, when the wound response signature is activated, the tumor grade is poorly differentiated, and without chemotherapy, the median survival time is 8 years. Similarly, at mean level of age, diameter and lymph node number, when the wound response signature is activated, the tumor grade is poorly differentiated and with chemotherapy, the median survival time is 14 years. The median survival time increases to 33.2 years when the wound response signature is quiescent, with chemotherapy, and other factors holding constant as above. They indicate that patients with chemotherapy have lower hazard rate and longer median survival time compared to those without chemotherapy when other factors are fixed. Based on both studies, time to death and time to metastasis, wound response signature can be used to predict survival probability and relative risk for early breast cancer patients.
6. Discussion
The author studied some predictor variables including clinical and gene expression variables for survival time associated with death due to breast cancer and metastasis in this article. Age of patients, diameter of tumor, tumor grade and wound response signature are the common risk factors that can be used to predict the survival probability related with both events. Among these risk factors, wound response signature is found to be a significant gene expression variable that is consistent with the result in other studies. The analysis performed is from a statistical point of view; clinical justification needs to be considered in practice.
Table 3. Analysis of risk factors for metastasis for four comparison models.
Lymph represents number of positive lymph nodes; Chemo represents chemo therapy status, without chemo therapy vs. with chemo therapy.
Based on the results of model comparisons for both events, the hypertabastic proportional hazards model outperforms all the comparison models. More applications can be considered to further study the property of this model. Weibull and log-logistic models performed better than the Cox model with lower AIC and BIC values. In the Cox model, the baseline hazard function is regarded as a nuisance parameter, while in parametric models, the hazard function reflects the time course of the process under study. Result indicates that parametric models provide a better fit to the breast cancer data.
In addition, hypertabastic accelerated failure time model (AFT model) was also introduced by Tabatabai et al. [7] , and has been applied to a medical data and an engineering data by Tabatabai et al. in [7] and [13] respectively. The hypertabastic AFT model also shows flexibility and performs well compared with other models. In case the proportional hazards assumption is not satisfied, AFT model should be applied to study the survival probability. The assessment of the performance of the hypertabastic AFT model will be a topic of our future research.
Conflict of Interests
The author declares that there is no conflict of interests regarding the publication of this paper.
Cite this paper
Li, H. (2017) Survival Analysis for a Breast Cancer Data Set. Advances in Breast Cancer Research, 6, 1-15. http://dx.doi.org/10.4236/abcr.2017.61001
References
- 1. Hosmer, D.W. and Lemeshow, S. (1999) Applied Survival Analysis: Regression Modeling of Time to Event Data. Wiley, New York.
- 2. Klein, J.P. and Moeschberger, S. (1997) Survival Analysis: Techniques for Censored and Truncated Data. Springer, Berlin.
https://doi.org/10.1007/978-1-4757-2728-9 - 3. Therneau, T.M. and Grambsch, P.M. (2000) Modeling Survival Data. Springer, Berlin.
- 4. Foulkes, M.A., Sacco, R.L., et al. (1994) Parametric Modeling of Stroke Recurrence. Neuroepidemiology, 13, 19-27.
https://doi.org/10.1007/978-1-4757-3294-8 - 5. Kannan, N., Raychaudhuri, A. and Pilamanis A.A. (1998) A Log Logistic Model for Altitude Decompression Sickness. Aviation, Space and Environmental Medicine, 69, 965-970.
https://doi.org/10.1159/000110354 - 6. Sama, W., Dietz, K. and Smith, T. (2006) Distribution of Survivial Times of Deliberate Plasmodium Falciparum Infections in Tertiary Syphilis Patients. Transaction of the Riyal Society of Tropical Medicine and Hygiene, 100, 811-816.
https://doi.org/10.1016/j.trstmh.2005.11.001 - 7. Tabatabai, M., Bursac, Z., Williams, D. and Singh, K. (2007) Hypertabastic Survival Model. Theoretical Biology and Medical Modeling, 4, 40.
https://doi.org/10.1186/1742-4682-4-40 - 8. Van de Vijver, M.J., He, Y.D., Van’t Veer, L.J., et al. (2002) A Gene-Expression Signature as a Predictor of Survival in Breast Cancer. NEJM, 347, 1999-2009.
https://doi.org/10.1056/NEJMoa021967 - 9. Tabatabai, M., Eby, W., Nimeh, N., Li, H. and Singh, K. (2012) Clinical and Multiple Gene Expression Variables in Survival Analysis of Breast Cancer: Analysis with the Hypertabastic Survival Model. BMC Medical Genomics, 5, 63.
https://doi.org/10.1186/1755-8794-5-63 - 10. Chang, H., Nuyten, D., et al. (2005) Robustness, Scalability, and Integration of a Wound-Response Gene Expression Signature in Predicting Breast Cancer Survival. PNAS, 102, 3738-3743.
https://doi.org/10.1073/pnas.0409462102 - 11. Troester, A.M., Lee, H.M., et al. (2009) Activation of Host Wound Responses in Breast Cancer Microenvironment. Clinical Cancer Research, 15, 7020-7028.
https://doi.org/10.1158/1078-0432.CCR-09-1126 - 12. Hosmer, D.W. and Lemeshow, S. (1989) Applied Logistic Regression. Wiley, New York.
- 13. Tabatabai, M., Asce, M., et al. (2011) Reliability of Bridge Decks in Wisconsin. Journal of Bridge Engineering, 16, 53-62.
https://doi.org/10.1061/(ASCE)BE.1943-5592.0000133
Abbreviations
WRS: Wound response gene expression signature;
ER: Estrogen receptor status;
AIC: Akaike Information Criterion;
BIC: Bayesian Information Criterion.
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact abcr@scirp.org






