Received 15 September 2015; accepted 27 November 2015; published 30 November 2015

ABSTRACT

This study presents an analysis of the impact of asset price bubbles on standard credit risk measures, including Expected Loss (“EL”) and Credit Value-at-Risk (“CVaR”). We present a styled model of asset price bubbles in continuous time, and perform a simulation experiment of a 2 dimensional Stochastic Differential Equation (“SDE”) system for asset value determining Probability of Default (“PD”) through a Constant Elasticity of Variance (“CEV”) process, as well as a correlated a Loss- Given-Default (“LGD”) through a mean reverting Cox-Ingersoll-Ross (“CIR”) process having a long- run mean dependent upon the asset value. Comparing bubble to non-bubble economies, it is shown that asset price bubbles may cause an obligor’s traditional credit risk measures, such as EL and CVaR to decline, due to a reduction in both the standard deviation and right skewness of the credit loss distribution. We propose a new risk measure in the credit risk literature to account for losses associated with a bubble bursting, the Expected Holding Period Credit Loss (“EHPCL”), a phenomenon that must be taken into consideration for the proper determination of economic capital for both credit risk management and measurement purposes.

Keywords:

Financial Crisis, Credit Risk, Model Risk, Asset Price Bubbles, Expected Loss, Credit Val-Ue-At-Risk, Stochastic Differential Equations, Probability of Default, Loss Given Default, Constant Elasticity of Variance, Cox-Ingersoll-Ross

1. Introduction

The financial crisis of the last decade has been the impetus behind a movement to better understand the relative merits of various risk measures, classic examples being Value-at-Risk (“VaR”) and related quantities (Jorion, 2006; Inanoglu & Jacobs, 2009) . The importance of an augmented comprehension of these measures is accentuated in the realm of credit risk, as the price bubble in the housing market and the ensuing credit crunch is undoubtedly a catalyst for the financial crisis. We have subsequently learned from this that the credit models of that era fail in not incorporating the phenomenon of price bubbles, which in turn add to the severity of the downturn for investors and risk managers who mis-measured their potential adverse exposure to credit risk. This manifestation of model risk (The US Board of the Governors Federal Reserve System, 2011) is due to some extent to a lack of basic understanding, wherein a modeling framework lacks a key element of an economic reality and there for fails. This failure of the modeling paradigm in credit risk spans gaps in the measurement, characterization and economics of asset price bubbles.

In view of analyzing the impact of asset price bubbles on credit risk measures and credit capital determination with respect to a firm subject to default risk, we construct various hypothetical economies having and also not having asset price bubbles. In a stylized structural credit model framework (Merton, 1974) , we simulate a firm’s value process in each of these economies, computing the firm’s standard risk measures. We present a model of asset price bubbles in continuous time, and perform a simulation experiment of a 2 dimensional Stochastic Differential Equation (“SDE”) system for asset value determining Probability of Default (“PD”)¹ through a Constant Elasticity of Variance (“CEV”)² process, as well as a correlated a Loss-Given-Default (“LGD”)³ through a mean reverting Cox-Ingersoll-Ross (“CIR”) process having a long-run mean dependent upon the asset value. Comparing bubble to non-bubble economies, it is shown that asset price bubbles may cause an obligor’s traditional credit risk measures such as Expected Loss (“EL”) and Credit Value-at-Risk (“CVaR”) to decline, due to a reduced standard deviation and an increased right skewness of the credit loss distribution. We propose a new risk measure in the credit risk literature to account for losses associated with a bubble bursting, the Expected Holding Period Credit Loss (“EHPCL”), a phenomenon that must be taken into consideration for the proper determination of economic capital for both credit risk management and measurement purposes.

The results of our experiment demonstrate that the existence of an asset price bubble, which occurs for certain parameter settings in the CEV model, results in the firm asset value distribution having both a lower standard deviation and a greater right skewness. This augmented right skewness in conjunction with a reduced variance of a firm’s return due to bubble expansion results in a reduction of the right skewness in the distribution of the default rate and a lower PD, which in combination with a lower mean of the LGD process, results in a credit loss distribution having lower mean right skewness and standard deviation. This in turn implies results in the firm’s CVaR measures declining, an understatement in the credit risk of the firm. Based on these measures alone, their declining values imply that in the presence of asset price bubbles, less credit capital is required. However, as shown by the additional risk measure proposed in the present paper, the EHPCL, this conclusion is incorrect. This credit loss measure increases in bubble economies and is due to bubble bursting, which causes significant firm value losses on the bubble-bursting paths.

As asset price bubbles are inevitably bound to burst, causing significant credit loss to creditors, more credit capital should be held for these bubble-bursting scenarios. Unfortunately, the se-verity of these bubble-bursting scenarios is not adequately captured by the standard credit risk measures, whose computation is based on the standard moments and quantiles of a firm’s credit loss distribution over time horizons such as a year, over which bubble bursting is unlikely. These bubble-bursting scenarios are captured, however, in some correctly constructed credit risk measures such as the EHPCL.

An outline for this paper is as follows. Section 2 presents a review of the literature. Section 3 presents our credit model incorporating the effect of asset price bubbles. Section 4 describes the results of our simulation experiment, while Section 5 summarizes the implications of our analysis for credit risk management.

2. Review of the Literature

Modern credit risk modeling (e.g. Merton, 1974 ) increasingly relies on advanced mathematical, statistical and numerical techniques to measure and manage risk in credit portfolios. This gives rise to Model Risk (Federal Reserve Board of Governors, SR 11-7), defined as the potential that a model used to assess financial risks does not accurately capture those risks, and the possibility of understating inherent dangers stemming from very rare yet plausible occurrences perhaps not in reference data-sets or historical patterns of data⁴, a key example of this being the inability of the credit risk modeling paradigm to accommodate the phenomenon of asset price bubbles.

The relative merits of various risk measures, classic examples being Value-at-Risk (“VaR”) and related quantities, have been discussed extensively by prior research (Jorion, 1997, 2006) . Risk management as a discipline in its own right, distinct from either general finance or financial institutions, is a relatively recent phenomenon. A general result of mathematical statistics due to Sklar (1956) , allowing the combination of arbitrary marginal risk distributions into a joint distribution while preserving a non-normal correlation structure, readily found an application in finance. Among the early academics to introduce this methodology is Embrechts et al. (1999, 2002, 2003) . This was applied to credit risk management and credit derivatives by Li (2000) . The notion of copulas as a generalization of dependence according to linear correlations is used as a motivation for applying the technique to understanding tail events in Frey & McNeil (2001) . This treatment of tail dependence contrasts to Poon et al. (2004) , who instead use a data intensive multivariate extension of extreme value theory, which requires observations of joint tail events.

Since the 2007 crisis, the mathematical finance literature has made significant advances in the modeling and testing of asset price bubbles (Jarrow & Protter, 2010; Hong et al., 2006) . Inanoglu & Jacobs (2009) contribute to the modeling effort by providing tools and insights to practitioners and regulators, utilizing data from major banking institutions’ loss experience, exploring the impact of business mix and inter-risk correlations on total risk, and comparing alternative established frameworks for risk aggregation on the same data-sets across banks. Protter (2011) , Protter et al. (2010) and Jarrow et al. (2014) apply these new insights to determine the impact, if any, that asset price bubbles have on the common risk measures used in practice for the determination of equity capital, which we extend to the realm of credit risk.

3. A Credit Model for Asset Price Bubbles

We model the evolution of asset prices, incorporating the phenomenon of price bubbles, using the approach of Jarrow et al. (2007, 2015) . The setting is a continuous trading economy, without loss of generality having a and finite horizon, with randomness described by the filtered probability space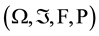, where we define:

the state space, the -algebra, the information partition, and the physical probability

measure (or actuarial, as contrasted to a risk-neutral probability measure, commonly denoted by the symbol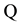). We assume, again without loss of generality and for the purpose on focusing on the application to cre-

dit loss, a single asset value process 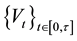that is adapted to the filtration. Note that this could also

represent a share of stock owned by a representative equity investor, which is a claim on the single productive entity or firm in this economy. In the general setting, follows an Ito diffusion process (Øksendal, 2003) having the following SDE representation:

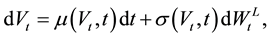(3.1)

where μ(V_t, t) is the instantaneous drift process, is the instantaneous diffusion process,

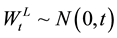
is a standard Weiner process (or a Brownian motion process) on the filtered probability space, and are its infinitesimal increments. In order to complete this economy, we assume that there exists a traded money market account process, which grows according to a risk-free rate process, the latter also adapted to the filtration of the aforementioned probability space:

(3.2)

Without loss of generality we assume that the asset has no cashflows, which could have been incorporated into the model by assuming a dividend process and studying the dividend-reinvested stock price process (Back, 2010) , but tomaintain simplicity of notation we do not do not do so.

We model an economy potentially having an price bubbles through the assumption that the risky asset’s prices follows a Constant Elasticity of Variance (CEV) process, as in Jarrow et al. (2014) , which is the following restricted version of the Ito diffusion process in (3.1):

(3.3)

where is the drift, is the volatility and the CEV parameter governs the state of the risky asset price process exhibiting a price bubble or not. An asset price bubble is defined as the situation where the market price for an asset exceeds its fundamental value (Jarrow et al., 2007, 2010) , the latter being defined conventionally price an investor would pay to hold the asset perpetually without rebalancing. This fundamental value is determined through the imposing some additional structure on the economy, requiring at minimum two additional assumptions. First, we need to assume that the absence of any arbitrage opportunities (Delbaen & Schachermayer, 1998) , which guarantees the existence of a risk-neutral probability measure equivalent to, such that the asset value process normalized by the money market account is a local Martingale process, following restricted version of the Ito diffusion process in (3.1):

(3.4)

where is the stopped process of and is a sequence of stopping times that

satisfy certain technical condition.⁵ The mechanism in (3.4) involving the risk-neutral probability measure affords us a means of computing present values where we shift the mass of the probability distribution (magnitude of the cash-flows) such that we can recover the same prices as under actuarial measure with the original cash- flows-but note that is arbitrary. In order to pin down this risk-neutral distribution, we assume from this point on a complete market, which means that that enough derivatives on the risky assets trade in order to replicate its cash flows in a suitably constructed arbitrage portfolio. The first condition is satisfied because the CEV process given in expression (3.3) admits an equivalent local martingale measure, so by construction it satisfies the absence of arbitrage opportunities.⁶ Under this incremental structure that we impose upon the economy, an asset’s fundamental value given the time information set, is defined as the asset’s discounted future payoff from liquidation at time at horizon:

(3.5)

It follows that we may define the asset’s price bubble as the difference between the market price and its fundamental value:

(3.6)

Since as a conditional expectation, the fundamental value normalized by the value of the money market account is a martingale under, a bubble exists if and only if the asset’s normalized price is a strict local martingale and not a martingale under. In the case of the CEV process, it can be shown (Jarrow et al., 2011) that

the asset’s normalized price is a martingale under when in (3.3) (i.e. no asset price bubble),

and a strict-local martingale under where in that equation (i.e. an asset price bubble). Note that the boundary case of yields the geometric Brownian motion underlying the Black-Scholes-Merton (“BSM”) option pricing model (Merton, 1974) , which is called the BSM economy, and can be shown to exhibit no price bubble (Delbaen & Schachermayer, 1995) .

In order to model the distribution of credit loss in the structural modeling paradigm (Merton, 1974) , we define the unconditional loss process as an Ito process, similarly to the asset value process (3.1):

(3.7)

where ν(V_t, t) is the instantaneous drift process, is the instantaneous diffusion process,

is a standard Weiner process (or a Brownian motion process) on the filtered probability space, and are its infinitesimal increments. We assume that is independent of, but model the correlation between and through making the drift of the latter dependent on the former as follows:

(3.8)

Therefore, for the linear drift function of is decreasing in. Next, we develop the distribution of credit loss by defining an event of default as asset value falling beneath the value of debt (or the default threshold) the horizon times the loss-given-default:

(3.9)

We define expected credit loss as the expectation of this random variable under actuarial probability measure:

(3.10)

We may estimate this quantity as through numerical integration over simulations, which is simply the sample mean, which is a consistent and unbiased estimator of this sample moment:

(3.11)

Similarly, we may obtain estimators of the population standard deviation and of the population normalized skewness of this distribution, defined as:

(3.12)

(3.13)

by their sample analogues and:

(3.14)

(3.15)

These statistics are estimates of the credit loss distribution’s moments under the physical probability measure, characterizing the changes in the value of a defaultable instrument that includes both positive and negative mark-to-market values. In an credit risk management application, we are actually only interested in losses, to which end we seek to understand the right tail of the credit loss distribution, and compute various high quantile risk measures, such as the VaR (in market risk) CVaR (it analogue in credit risk). Apart from asset price bubbles, even though its limitations are widely known (Alexander, 2001; Jorion, 1997) , such measures are widely used in the industry.⁷ An estimator for the CVaR at a given confidence level c is given by:

(3.16)

where:

(3.17)

where is an indicator function that takes the value 1 if and 0 otherwise. We may also define a

conditional CVaR measure, the Expected Tail Credit Value-at-Risk (“ETCVaR”), as the expected loss conditional on credit loss being greater than or equal to loss at confidence level:

(3.18)

In order to model the influence of an entire boom to bust cycle of asset values upon credit risk measures, we introduce a measure of credit loss over a sequence of smaller sub-intervals, which we call the Expected Holding Period Credit Loss (“EHPCL”). Let be a shorter 1-week (5 days) holding period, be the longer 1-year (250 day) horizon of the simulation and is the number of consecutive sub-intervals of length (50 weeks). Then we define the day credit loss for sub-period along simulation path

as a situation in which it is greater than the estimated expected loss over the simulation horizon

:

(3.19)

Then we define the as the average of this quantity over sub-intervals and over simulation paths:

(3.20)

Finally, we make note that we may look at all of these measures on a relative basis, scale by the, the estimators for which we omit for the sake of brevity.

4. A Simulation Experiment

We demonstrate the impact of asset price bubbles on an obligor’s credit risk measures, as defined in the previous section (i.e. EL, CVaR, ETCVaR and EHPCL), through a stochastic simulation experiment. Simulation is needed to determine the probability distribution of asset value, loss given default rate and ultimately the credit loss rate over a given time interval. In our experiment we fix the time period for the standard credit risk measures to be 250 trading days or one year, which is conventional for economic and regulatory credit risk capital calculations, with subintervals of one business week or five trading days for the EHPCL measure. We use simulation because an analytic solution for the firm value’s probability distribution using the CEV process is unavailable (Emanuel & MacBeth, 1982; Schroder, 1989) .⁸

We perform the simulation experiment through constructing a collection of different economies, some with bubbles and some without, by varying the CEV parameter from 0.25 to 2.0 in steps of size 0.25. n each of these different economies, we compute the standard risk measures to determine the impact that bubbles have on their values. We fix the other parameters of the simulation as follows. Asset value is initiated at a normalized value of one, with a drift rate of 5% per annum, , and a volatility parameter of 10% per annum,. Default is assumed to occur is asset value at the horizon is below the debt threshold of 0.80,. The mean reversion parameter of the LGD process is set to be, and the sensitivity of the long-run mean to asset value is set to, with an initial value; and a diffusion function having volatility of and CEV parameter.

The results of our sssanalysis are tabulated in Table 1 and Table 2, and in Figures 1-10. In Table 1 we present

the absolute credit loss measures as defined in Section 3, whereas in Table 2 we present these measures on a relative basis, scale by the expected credit loss. We also show the estimate of PD and the distributional statistics of

the asset value, LGD and credit loss processes. Figure 1 and Figure 2 plot some key credit loss measures against the values of the CEV parameter, both in absolute and relative terms with respect to EL, respectively. Figures 2-10 plot the distributions of asset value, LGD and credit loss processes, as well as the simulation paths

of the asset value and LGD processes.

We can see from the results that all of the standard risk measures decrease as we increase the CEV parameter into the region where we have an asset price bubble, whereas the EHPCL increases montonically and at an

increasing rate as this parameter grows. We observe that this is driven by a change in the asset value process as rises, as we observe the skewness to rise monotonically and dramatically, doubling from 0.3089 to 0.6485 as we go from Geometric Brownian Motion (GBM) at to a bubble economy with. Note that other features of the asset value distribution are largely unchanged, such as the mean or the standard deviation, as we

increase. Note further that we see increasing asset value skewness in even when in the non-bubble region, with skewness about quadrupling from 0.08 to 0.31. On the other hand the LGD process does not have a very pronounced decrease in skewness as we increase, and the pattern is non-monotonic, although from BGM to a CEV parameter of 2 LGD skewness decreases from 0.80 to 0.64, which is significant; and as with asset value, other features of the distribution are basically unchanged, including the mean, which is surprising in that the drift is a function of the asset value process. The effect of the asset value process can be seen in the average PD in each simulation, decreasing monotonically from 0.66% for, to 0.39% for, and finally to 0.07% for.

In the bottom panel of Table 1 we show the various credit loss metrics as a functions of the CEV parameter, and observe that all of the standard measures are declining in. The ECL decreasing monotonically from 0.24% for, to 0.14% for, and finally to 0.03% for. All of these CVaR measures also decline montonically and at an accelerating pace in, and the steepness of the decline actually increases as the confidence level becomes more conservative. For instance, for the 99.97^th percentile CVaR, it decreases monotonically and at an accelerating rate in from 0.54% for, to 0.27% for, and finally to 0.03% for. The standard deviation of credit loss also decreases monotonically and at an accelerating rate from 0.14% for, to 0.07% for, and finally to 0.01% for. In contrast, the EHPCL increases monotonically and at an accelerating rate in from 0.34% for, to 0.46% for, and finally to 0.88% for. This is a reflected in the declining skewness of the credit loss distribution in from 1.05 for, to 0.49 for, and finally to −27 for―implying that skewness this is a robust indicator of a bubble, but does not have the benefit of having an intuitive economic interpretation as does the EHPCL.

In the bottom panel of Table 2 we show the various relative credit loss metrics (scaled by ECL) as a functions of the CEV parameter, and observe that all of the standard relative risk measures are declining in, as are the absolute versions in Table 1. All of three relative CVaR measures also decline montonically and at an accelerating pace in, and the steepness of the decline actually increases as the confidence level becomes more conservative. For instance, for the 99.97th percentile CVaR to ECL ratio, it decreases monotonically in from 2.27 for, to 1.88% for, and finally to 1.23% for. The standard deviation to ECL ratio also decreases monotonically and at an accelerating rate from 0.57 for, to 0.47 for, and finally to 0.39 for. In contrast, the EHPCL to ECL ratio increases monotonically and at an accelerating rate in from 1.33% for, to 3.28 for, and finally to 35.11 for. This is a reflected in the declining ratio of skewness to ECL ratio in from 440.72 for, to 346.17 for, and finally to −1062.11 for.

5. Conclusion and Future Directions

In this study, we have analyzed the impact of asset price bubbles on credit risk measures for a representative firm subject to default risk. We have constructed various hypothetical economies, both having and also not having asset price bubbles in a structural credit model framework. We have simulated a firm’s value process in each of these economies, computing the firm’s standard risk measures, in continuous time, performing a simulation experiment of a 2-dimensional system of SDEs for asset value determining PD and a correlated a LGD process. Comparing bubble to non-bubble economies, it has been shown that asset price bubbles may cause an obligor’s traditional credit risk measures (such as EL or CVaR) to decline, due to a reduced standard deviation and a reduced right skewness of the credit loss distribution (driven by an augmented right skewness of the asset value distribution). We have developed the new EHPCL credit risk measure to account for losses associated with a bubble bursting, which behaves intuitively as we transition from non-bubble to bubble economies.

The results of our experiment have demonstrated that the existence of an asset price bubble, which occurs for certain parameter settings in the CEV model, results in the firm asset value distribution to have both a lower standard deviation and a greater right skewness. We have demonstrated that this augmented right skewness, in conjunction with a reduced variance of a firm’s return due to bubble expansion, results in a reduction of the right skewness in the distribution of the default rate and a lower PD, which in combination with a lower mean of the LGD process, results in a credit loss distribution having both lower mean right skewness and lower standard deviation. This in turn implies a decline in the firm’s CVaR measures and an understatement in the credit risk of the firm. Based on these measures alone, their declining values imply that in the presence of asset price bubbles, less credit capital is required. However, we have shown that according to the new EHPCL, this conclusion is incorrect, as this EHPCL credit loss measure increases in bubble economies and is due to bubble bursting, which causes significant firm value losses, and therefore credit losses, on the bubble-bursting paths.

In the detailed analysis of the results, we have shown that the various credit loss metrics are all declining functions of the CEV parameter: The ECL is decreasing monotonically in, and also all of the CVaR measures decline montonically at an accelerating pace in, with the steepness of the declining actually becoming accentuated as the confidence level becomes more conservative. This is shown to be reflected in the declining skewness of the credit loss distribution in, implying that skewness is a robust indicator of a bubble; however, it does not have the benefit of having an intuitive economic interpretation as does the EHPCL.

There are various avenues down which we may proceed in the interest of pursuing additional research. One such direction will be an extension to a structural model that can admit differential seniority for LGD, an option-theoretic approach along the lines of Jacobs (2011, 2012) . Another potential sequel to this study will be the analysis of a real portfolio of equities and empirical calibration, along the lines of Jarrow et al. (2015), although in the context of credit as opposed to market risk. Finally, we may investigate more general stochastic diffusion models for asset value, such as the incorporation of jump processes.

Cite this paper

MichaelJacobs Jr., (2015) The Impact of Asset Price Bubbles on Credit Risk Measures. Journal of Financial Risk Management,04,251-266. doi: 10.4236/jfrm.2015.44019

References

NOTES

¹For a Bayesian stochastic model for PD in the Basel Asymptotic Single Risk Factor (“ASRF”) class of models, underlying the Basel II Advanced IRB model for credit loss, see Jacobs & Kiefer (2010) .

²For applications of the CEV model in finance see Chan et al. (1992) and Jacobs (2001) , in the context of term structure and interest rate derivatives.

³See Jacobs (2011, 2012) for a 2-factor structural credit model with stochastic LGD; Araten & Jacobs (2004) or Jacobs & Karagozoglu (2011) for empirical models of LGD; and Frye & Jacobs (2012) for a structural credit risk model in ASRF class of models, featuring co-monotonic LGD and PD that provides a parsimonious function for downturn LGD.

⁴In the wake of the financial crisis (Demirguc-Kunt et al., 2010; Acharya et al., 2009), international supervisors have recognized the importance of Stress Testing (ST), especially in the realm of credit risk, as can be seen in the revised Basel framework (BCBS 2005, 2006, 2009a, 2009b, 2010) and the Federal Reserve’s Comprehensive Capital Analysis and Review (“CCAR”) program (Jacobs 2013, Jacobs et al. 2015) .

⁵The conditions are that is almost surely increasing and is almost surely divergent (Oksendal, 2003).

⁶This condition is sometimes termed “no free-lunch with vanishing risk” or NFLVR (Jeanblanc et al., 2009) .

⁷This is partly due to the Basel II Accords (Engelmann & Rauhmeier, 2006; Cornford, 2005) .

⁸We use the R package Sim. DiffProc to simulate the 2-imensional system of SDEs for asset value and for LGD (Development Core Team, 2015) .