Journal of Financial Risk Management
Vol.03 No.04(2014), Article ID:51389,7 pages
10.4236/jfrm.2014.34012
Quantitative Risk Analysis of the Futures Company’s Own Business Based on VaR Model
Jianfei Len, Xu Gao, Guorong Jia
School of Business, Hohai University, Nanjing, China
Email: ljf200209@163.com, 1278047887@qq.com
Academic Editor: Siqiwen Li, James Cook University, Australia
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 August 2014; revised 4 October 2014; accepted 21 October 2014
ABSTRACT
In this paper, we use the futures exchange copper trading data of Shanghai as a sample for the VaR quantitative analysis. Through empirical analysis, the results showed that VaR method based on GARCH model can be a good fit in the insurance value of copper futures. Therefore, we can consider it as an important means of futures risk management in our country, and with reference t to establish corresponding risk warning system.
Keywords:
Futures Company, VAR, Proprietary Business

1. Introduction
“Futures Company’s asset management business pilot approach” with official purposes since September 1, 2012, has attracted the attention of the entire industry and was considered as the most important innovation in 2012 in the domestic futures market. The move means that while in the near future, proprietary trading futures company may also subsequently appeared, and provide a more effective means for our futures companies to solve the dilemma of profit and create new profit growth.
VaR model has now become a mainstream market risk management model which the foreign financial intermediaries prefers to, and it also studies using VaR model to measure the other risks, such as the feasibility of credit risk, market risk, etc. Ederington (1994) combined with the actual situation of self-employed business, studied the use of minimum variance model optimal hedge ratio to control the import and business risks. Khindanova, Rachev & Schwartz (1999) argued that using covariance, historical simulation and Monte Carlo simulation and pressure testing of the traditional method to calculate VaR had poor effect, and they proposed to use Palmer le temple distribution to establish VaR model. Cuoco, He & Issaenko (2001) found that using VaR risk management must assess the VaR indicators dynamically depending on the circumstances, and using VaR to control trading risk effect is remarkable. Jorion’s (2005)
study pointed out that Goldman Sachs, Merrill Lynch, JP Morgan et al. established a set of core proprietary business VaR as risk management and control system, using Monte Carlo simulation and other modern financial technology to manage proprietary business risk, which ensures the quality of the self-employed business.
And in China, scholars also have a lot of related research. Hu (1999) in the book “An Introduction to The Securities Company Risk Management” pointed out that the financial industry is a high-risk industry and the financial intermediary company to control risk should draw lessons from western advanced risk control method, and the introduction of the mathematical model to strengthen the quantitative analysis of risk control at the same time. Yao (2002) argued that if the company proprietary for effective risk control, certainly will form the huge losses and propose VaR method to measure the company proprietary investment risk to determine the moderate scale of proprietary investment. Li (2005) argued that the risk management system construction should include: the framework of risk management organization structure; the importance of VaR which is the core of risk monitoring system; and the construction of comprehensive risk management system, etc.
2. Value at Risk VaR Theory
2.1. Introduction of VaR
VaR (Value at Risk), also known as at Risk, refers to the given confidence level and the normal market conditions, investors in one day, a week, a year the biggest loss within a specified time frame, or in normal market conditions, and for a given period of time, a portfolio of VaR value loss probability.
2.2. The Application of VaR in Risk Management
VaR main application is reflected in: first, to control the risk. Using the VaR method to control the risk can make trading unit or each trader can clear understanding of how they are engaged in risk investment transactions and on the basis of it can be set for trading or each trader VaR limitation, to prevent excessive speculation; Second, for the company's performance evaluation. Financial institutions for the purpose of stable operation, traders must be possible to limit the excessive speculation. So, the introduction of considering risk factors of performance evaluation index is necessary; Third, the estimation of risk capital. Through VaR calculations, to estimate the investors in the face of the market risk for a moderate amount of venture capital, venture capital requirements are a basic requirement for financial regulation.
3. The Futures Company Proprietary Risk Quantitative Analysis
3.1. The Calculation of VaR and GARCH Model
3.1.1. The Calculation of VaR
Theory of VaR value at risk is refers to under certain confidence level, asset portfolio or portfolio in the future a period of time may be the biggest loss. That is:
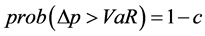 (1)
(1)
where, Δp is assets in the holding period of loss; VaR is the confidence level c of value at risk; C is the confidence level.
To simplify the calculation, the commonly used GARCH model to measure the volatility, and the sequence of assets normal distribution is assumed. By type (1), when the confidence level c, asset holding period after standardization, VaR value can be obtained, namely the asset return sequence of the left tail maximum loss:
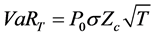 (2)
(2)
where type of P0 is initial value of the assets, sigma for variance, Ζc is confidence level, T is asset holding period.
3.1.2. Inspection of VaR
After calculating the VaR value, it is necessary to estimate the results of testing. Failure Test is the most commonly used test after testing, it is by comparing the frequency of the actual loss more than VaR and the upper limit of under a certain confidence level is close to or equal, which to determine the effectiveness of the VaR model. If the model is valid, the failure rate of the model should be equal to the preset VaR confidence (1 ? c), the difference between (1 ? c) if the failure rate is bigger, showing that model is not appropriate. Assumes that the confidence level for c, actual investigation the number of days for T, failed days to N, the failure rate for p(=N/T), such failure rate is subject to a binomial distribution, expecting probability is p*, the original hypothesis for H0: p = p*., alternative hypothesis for the H1: p ≠ p*, whether to reject null hypothesis test failure frequency. Kupiec (1995) proposed that the likelihood ratio test is adopted to zero hypothesis test, and the likelihood ratio equation is:
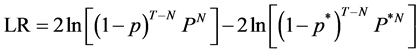 (3)
(3)
Of formula (3) under the null hypothesis conditions LR statistic distribution of degrees of freedom is 1.
3.1.3. GARCH Model
The general expression GARCH (q, p) model is:
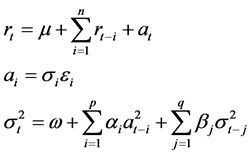 (4)
(4)
where 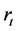 for the return series,
for the return series, 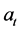 for the residuals,
for the residuals, 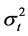 for the conditional variance,
for the conditional variance, 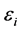 for independent.
for independent.
Zakoian, et al. (1990), based on this, advanced the TARCH or Threshold ARCH Threshold (ARCH) model, the conditional variances into:
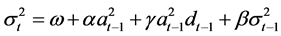 (5)
(5)
Nelson (1990) proposed the allowed and is more flexible than quadratic equation index GARCH model of the relationship between the EGARCH model conditional variances into:
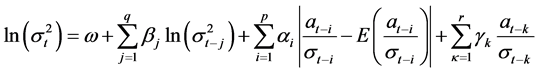 (6)
(6)
Ding et al. (1993) proposed PARCH model, conditional variance equation form PARCH model is:
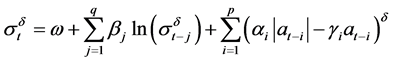 (7)
(7)
Thus, we calculate the conditional variance, and then to predict earnings and variance, using predicted income and the corresponding probability distribution and variance under quantile can be substituted into (2) determine the future VaR value of T time.
3.1.4. About Distribution
In GARCH model residual distribution usually have three: a normal (Gaussian) distribution, student t-distribu- tion and generalized error distribution (Generalized Error Distribution, GED). Nelson and Hamilton, who made use of the student t-distribution and generalized error distribution to reflect the characteristics of its tail spikes. Student t-distribution probability density function is:
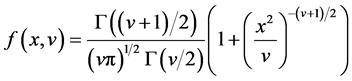 (8)
(8)
where Γ(・) is the Gamma function, v is the degree of freedom, when v approaches ∞, t-distribution converges to the normal distribution. GED distribution probability density function is:
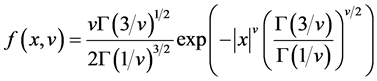 (9)
(9)
3.2. Descriptive Statistics
According to Table 1, from 2002 to 2002, China’s three major futures exchanges in clinch a deal amount of the transaction volume percentage, the Shanghai futures exchange years accumulative total clinch a deal amount of the share of average is 48.81%, far more than the Zhengzhou Commodity Exchange and the Dalian commodities exchange. So choose the Shanghai futures exchange trading data for quantitative analysis of the VaR is more representative.
According to Table 2, which shows that from 2002 to 2011, Shanghai has all the transaction data, and compared with the other trades, Shanghai copper all the years of accumulated clinch a deal amount of the share percentage of deals were greater than other trades, so choose in the Shanghai futures exchange trading data of Shanghai copper VaR study more representative.
Table 1. Cumulative share of the country’s total gross turnover.
Data sources: China futures industry association website (http://www.cfachina.org).
Table 2. Shanghai futures exchange trading varieties each year cumulative total turnover of the country’s total share.
Data sources: China futures industry association website (http://www.cfachina.org).
3.3. Data Selection
Because of the VaR model itself to the requirement of data, this paper selected the Shanghai futures exchange trading in Shanghai for a longer time daily settlement price, during the data for January 5, 2012 to September 24, 2012, excluding holidays a total of 177 days. Chosen for the cause of the Shanghai daily settlement price is listed on the Shanghai exchange, early data comprehensively, and is a representative of the futures market development, the change of the index can more accurately reflect the market changes direction.
3.4. The Empirical Test
3.4.1. Data Normality Test
There are many normal test methods; the simplest method is to test skewness and kurtosis test. Using Eviews, analysis of the copper index logarithmic normality test results was shown in Figure 1.
As can be seen from the figure above, there is a certain day yield characteristics of normality, but it does not obey the standard normal distribution. Its average daily yield of 0.000256, −0.047806 skewness, kurtosis is 4.118310 3 larger than the standard normal distribution, showing the characteristics of a fat tail, which is more in line with theoretical estimates. The JB is much greater than 73.53960 significant level of 0.05 quantile 5.991, so the distribution is rejected the null hypothesis of normality. Logarithmic returns are not normally distributed, and have a left side, a fat tail nature.
3.4.2. Data Stationarity Test
With method of unit root test of time series, the results are shown in Table 3 below.
Table 3 shows, the ADF test day yield index futures time series t statistic −12.47478 less than 1% of the critical value −3.467633. Therefore, we can reject the null hypothesis at least at the 99% confidence level, the sequence does not exist unit root, is smooth.
Figure 1. Data normality test results.
Table 3. Data stationarity test results.
3.4.3. Yields of Autocorrelation Test
Considering the validity of the model, autocorrelation test was carried out on the yield. Through Eviews autocorrelation test of the data, we get the result. Because of the autocorrelation coefficient and partial correlation coefficient is not 0, significantly and Q statistic is significant, so can get its residual error sequence exists ARCH effect. So using GARCH (1, 1) model to estimate, usually model assumes that the residuals obey normal distribution, but in practice, gains sequences often there is a peak, thick tail, namely the distribution of returns on kurtosis kurtosis is high than the standard normal distribution. Distribution in thick tail risk managers are particularly worried about, because it means that the frequency of the excess loss is higher than the predictions of a normal distribution. Have in front of the logarithm yield of normality test, it is concluded that yield sequence is not normal distribution, so we used GARCH (1, 1) model to estimate, the results are shown in the Table 4.
3.4.4. GARCH Model to Build
Before the establishment of the GARCH model, using AIC information criterion repeated tests, AIC get minimum values when the lag order (p, q) is (1,1), so the following models are GARCH (1,1) class model. We’ve already come to mean yield of 0.000256, the table can be combined to build GARCH model equations yields:
Mean equation:
Variance equation: 
And then the residual model are heteroscedasticity LM test, the conclusion cannot reject the null hypothesis that the model does not consider the presence of residual heteroskedasticity and β values greater than 0.6, the
Table 4. GARCH (1, 1) model to estimate the result.
return value of the coefficient α is less than 0.25, you can explain this equation has strong explanatory power, can better describe the copper index yield heteroskedasticity phenomenon.
3.4.5. Shanghai Copper Futures Index Returns VaR Calculation
GARCH model with conditional variance to measure the futures market, which is calculated as follows:
Using Eviews, GARCH conditional variance sequences can be generated, the conditions of the conditional variance standard deviation obtained sequence evolution sequence, the figure is the standard deviation of the conditions GARCH model sequences, can be clearly seen from Figure 2, when the conditional variance has obvious degeneration, that change over time and depend on past values. With conditional VaR instead of the standard deviation obtained in the standard deviation is calculated to obtain statistics VaR at 95% confidence level, the following Table 5.
From the table above shows that the biggest risk income loss can reach 5.578978%, the smallest risk loss is 1.426879%, average risk loss is 3.698741%, the VaR of the standard deviation is 1.685201%.
3.4.6. Return to the Test (Table 6)
Under 5% significance level, the failure of the number of days should not be more than 9 days, otherwise the risk has the potential to underestimate. Test results show that the failure rate is far less than 5%, says the VaR better estimate the risk.
Through the above empirical analysis, we can find that VaR method based on the GARCH model can well fitting value at risk of Shanghai copper futures in our country. We can consider it as one of the important means of futures risk management in our country, and with reference to their corresponding risk early warning system.
Figure 2. The condition of standard deviation sequence of GARCH model.
Table 5. Conditions instead of the standard deviation standard deviation calculation of VaR.
Table 6. Return to the test.
4. Conclusion
Futures companies in our country can refer to the GARCH-VaR risk prediction model which can better describe the earnings volatility clustering effect. Research to establish the actual VaR mathematical model for the company self-service, companies can more accurately predict the risk of self-service trend. At the same time, VaR model should be linked with the board of directors of the self-management scale, the company’s net capital control indicators and some dynamic conditions.
Meanwhile, during the off-site inspection, it requires companies to calculate the daily VaR value based on a dynamic VaR model, with the provisions of the futures company’s risk capital reserves calculation standard for comparison and analysis of the impact on net capital. If the dynamic VaR value is higher than the prescribed percentage for the risk, then promptly the company is required to raise the proportion of risk capital to prepare, adjust the position and size of the operation strategy and re-calculate the net capital and other core risk control indicators. By the above method, the risk can be realized in real time, dynamic and advance monitoring.
References
- Cuoco , He, & Issaenko (2001). Foundations of Risk Measurement. Encyclopedia of Statistical Sciences, 8, 485-495.
- Ding, Z.X., et al. (1993). A Long Memory Property of Stock Market Returns and a New Model. Journal of Empirical Finance, 1, 83-106. http://dx.doi.org/10.1016/0927-5398(93)90006-D
- Ederington, H. L. (1994). The Hedging Performance of the New Futures Markets. The Journal of Finance, 34, 157-170. http://dx.doi.org/10.1111/j.1540-6261.1979.tb02077.x
- Hu, G. J. (1999). Introduction to Securities Companies Risk Management. Shanghai: Fudan University Press.
- Jorion, P. (2005). How Investment Bankers Determine the Offer Price and Allocation of New Issues. Journal of Finance Economics, 23, 43-162.
- Khindanova, Rachev, & Schwartz (1999). A Theory of Perceived Risk and Attractiveness. Organizational Behavior and Human Decision Processes, 52, 92-98.
- Kupiec, P. (1995). Techniques for Verifying the Accuracy of Risk Measurement Models. Journal of Derivatives, 3, 73-84. http://dx.doi.org/10.3905/jod.1995.407942
- Li, J.N. (2005). Securities Companies Risk Management Research. Nanjing: Nanjing Agricultural University.
- Nelson, D. (1990). ARCH Models as Diffusion Approximations. Journal of Econometrics, 31, 307-327
- Yao, X. Y., Teng, H. W., & Chen, C. (2002). The Size Risk Control of the Asset Management Business. The Number of Economic and Technical Economic Research, 5, 65-67.
- Zakoian, J. M. (1990). Threshold Heteroskedastic Model. Journal of Economic Dynamics and Control, 18, 931-955. http://dx.doi.org/10.1016/0165-1889(94)90039-6






