International Journal of Clean Coal and Energy
Vol.04 No.03(2015), Article ID:58558,7 pages
10.4236/ijcce.2015.43006
Multi-Objective Optimization for Active Disturbance Rejection Control for the ALSTOM Benchmark Problem
Chun’e Huang*, Zhongli Liu
The College of Biochemical Engineering, Beijing Union University, Beijing, China
Email: *hce137@163.com, *hchune@buu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 May 2015; accepted 2 August 2015; published 5 August 2015
ABSTRACT
Based on a thing that it is difficult to choose the parameters of active disturbance rejection control for the non-linear ALSTOM gasifier, multi-objective optimization algorithm is applied in the choose of parameters. Simulation results show that performance tests in load change and coal quality change achieve better dynamic responses and larger scales of rejecting coal quality disturbances. The study provides an alternative to choose parameters for other control schemes of the ALSTOM gasifier.
Keywords:
Gasification, Multi-Objective Optimization, Non-Dominated Sorting Algorithm II (NSGA-II), Active Disturbance Rejection Control (ADRC)

1. Introduction
Integrated gasification combined cycle (IGCC) power plants are being developed to provide environmentally clean and efficient power from coal. GEC ALSTOM developed a small-scale prototype integrated plant, based on air-blown gasification cycle (ABGC). The gasifier as a component of the ABGC is a highly coupled multi- variable system with five inputs and four outputs and is found to be particularly difficult to control.
In 1997, the ALSTOM Energy Technology Center issued an open challenge to the UK Academic Control Community to develop advanced control techniques for the linear model of the ALSTOM gasifier. The “challenge information pack” [1] comprises three linear models with detailed specifications, including output limits, control input constraints, and disturbance tests. In June 2002, the second round challenge [2] [3] was issued, and it extended the original study by providing the full non-linear model of the gasifier in M ATLAB/S IMULINK. Moreover, an expanded specification, which incorporates set point changes and coal quality disturbance, and a PI control strategy (also called the baseline control) introduced by Asmar [4] is included. More details of the gasifier can be found in [2] [3] .
Many advanced control approaches have been applied in the control of the non-linear ALSTOM gasifier, such as  methodology [5] ,
methodology [5] , 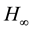 control [6] , PID control [7] , predictive control [8] , proportional-integral-plus (PIP) [9] , state estimation-based control [10] , PI control [4] [11] [12] , partially decentralized control [13] , and so on. Although the performance tests of some advanced control methods are satisfactory, the multi-variable control structure is so complex that it is not easy to implement in practice. Among the control of the non-linear ALSTOM gasifier, the PI control shows obvious advantages because of their simple structure and better response performance. Recently, the active disturbance rejection control (ADRC) scheme proposed by Huang [14] achieved better performances than the PI control. However, the tuning of the parameters is still a difficult thing.
control [6] , PID control [7] , predictive control [8] , proportional-integral-plus (PIP) [9] , state estimation-based control [10] , PI control [4] [11] [12] , partially decentralized control [13] , and so on. Although the performance tests of some advanced control methods are satisfactory, the multi-variable control structure is so complex that it is not easy to implement in practice. Among the control of the non-linear ALSTOM gasifier, the PI control shows obvious advantages because of their simple structure and better response performance. Recently, the active disturbance rejection control (ADRC) scheme proposed by Huang [14] achieved better performances than the PI control. However, the tuning of the parameters is still a difficult thing.
The non-dominated sorting genetic algorithm-II (NSGA-II) [15] is one of multi-objective evolutionary algorithms. Although many multi-objective evolutionary algorithms have been emerged, NSGA-II has attracted more and more attention for its fast non-dominated sorting, parameterless niching and elitist-preserving.
In the paper, based on the analysis of multi-objective optimal algorithm, NSGA-II is applied in the choice of parameters for ADRC schemes of the ALSTOM gasifier. Simulation results show that performance tests in load change and coal quality change achieve better dynamic responses and larger scales of rejecting coal quality disturbances. The content is arranged as follows: Section 2, ALSTOM gasifier model and control system specification are introduced; Section 3, NSGA-II for ADRC scheme of the ALSTOM gasifier is proposed, including the chose of objective function of multi-objective optimization, the results of the optimization and the performance tests; conclusion is given in Section 4.
2. ALSTOM Gasifier Model and Control System Specification
The gasifier is a non-linear, multi-variable component, and provided in the Challenge II of ALSTOM gasifier benchmark problem [3] . It is a reactor in which pulverized coal mixed with limestone, is conveyed by pressurized air into the gasifier, and gasified with air and injected steam, producing a low calorific-value fuel gas. The remaining char is removed from the base of the gasifier. The gasifier has five controllable inputs (coal, limestone, air, steam and char extraction) and four outputs (pressure, temperature, bed-mass and gas quality). In whole process, limestone is used to absorb sulphur in the coal, its flow rate must be set to a fixed ratio of coal flow, nominally 1:10 limestone to coal. This leaves a four-input four-output problem for the control design [1] . By the physical properties of the actuator devices, the non-linear gasifier model includes the input actuator flow limits and the rate of change limits, and the output limits, see [2] for details.
The control specification of the non-linear gasifier are listed as follows.
1) Pressure disturbance tests: A downstream pressure disturbance Psink, choosing from step disturbance of −0.2 bar or sine wave disturbance of amplitude 0.2 bar and frequency of 0.04 Hz, is applied to the gasifier, running the simulation 300 seconds; and calculate IAE index for the gas quality Cvgas and gas pressure Pgas over the complete run.
2) Load change tests: Start the system at 50% load in steady state and ramp it to 100% over a period of 600 seconds (5% per minute). The measured load should follow the load demand as closely as possible with minimal over shoot at the end of the ramp. The input constraints need to be adhered to the controller outputs all the time.
3) Coal variation test: Coal quality can change quite significantly depending on its source. It should be changed incrementally within the range ±18%, and any effect on the performance of the controller should be noted.
3. NSGA-II for ADRC Scheme of the ALSTOM Gasifier
In the control of the ALSOTM gasifier, the intension is that the performance tests would facilitate the evaluation of the closed-loop systems response to pressure disturbances, load changes and coal quality changes [2] . ADRC scheme of the ALSTOM gasifier was introduced by Huang [14] . In this case, the matching of the gasifier is listed as follows: gas calorific value with air flow, gas pressure with steam flow, gas temperature with char flow, and bed mass with coal flow, a feedforward and a proportional controller, three first-order active disturbance rejection controllers are designed to replace PI controllers in the baseline control. Thus, three ADRC controllers have four tuning parameters each, plus one parameter for the proportional control of bed mass and one for the feedforward gain to the coal flow (from char flow). More details can be found in original study [14] .
In ADRC scheme, the parameter 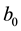 of each ADRC can be estimated based on the linear model in the first “Challenge Information Pack” [1] , the value
of each ADRC can be estimated based on the linear model in the first “Challenge Information Pack” [1] , the value ,
,  , and
, and 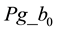 are listed as follows [14] :
are listed as follows [14] :
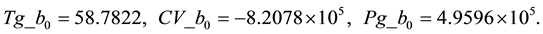
Moreover, the adding of ADRC gives rise to the order increase of the gasifier, the initial states x0c should be reset, and the initial values u0 of each ADRC can be initialized. The initial values x0c and u0 at three loads can be obtained using the suggested method [14] , as shown in Table 1.
3.1. The Formulation of Multi-Objective Optimization
In ADRC scheme, the parameter 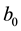 in each active disturbance rejection controller is fixed, there are three parameters
in each active disturbance rejection controller is fixed, there are three parameters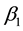 ,
, 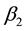 and
and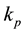 . Hence there are eleven parameters which needed to be adjusted. The optimized variable
. Hence there are eleven parameters which needed to be adjusted. The optimized variable 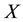 is represented as
is represented as
 (1)
(1)
The objective function is formulated as follows
 (2)
(2)
where m 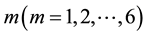 represent sequentially sine and step pressure disturbances at 100%, 50% and 0% loads;
represent sequentially sine and step pressure disturbances at 100%, 50% and 0% loads; 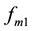 and
and 
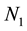
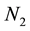
Table 1. Initial value x0c and u0 of ADRC scheme at three loads.
respectively;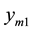
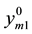
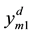
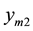
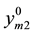

An index of coal quality flexibility was defined as follows [12] :
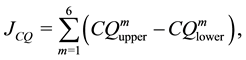
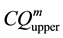
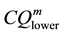
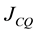
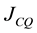
3.2. Results of Multi-Objective Optimization for the ALSTOM Gasifier
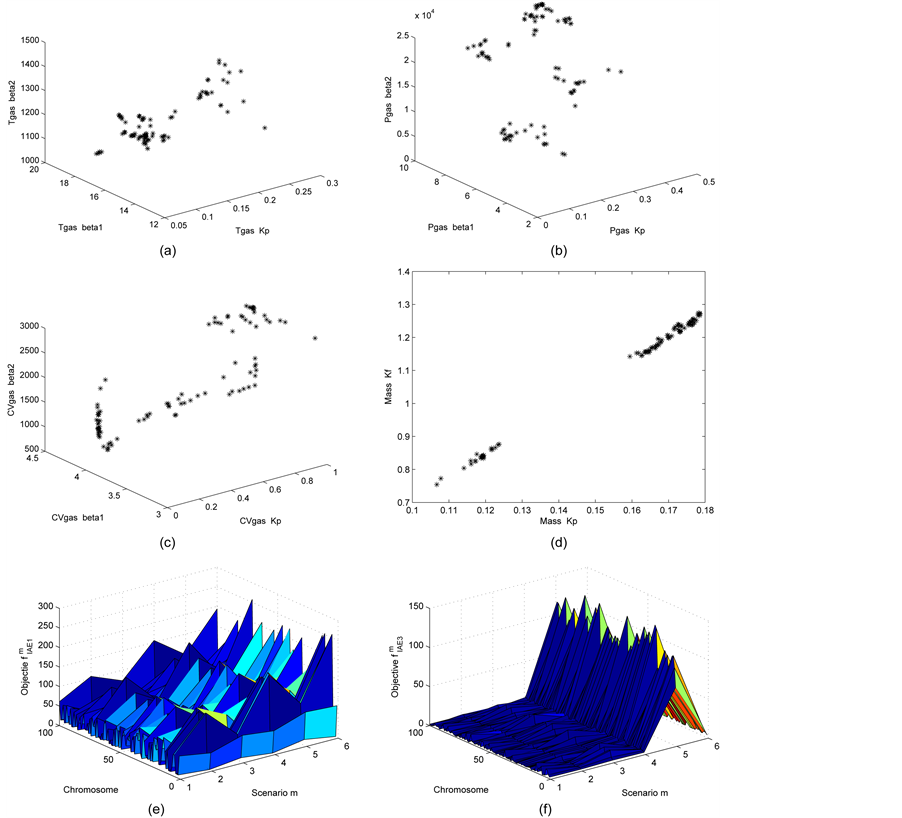
After multi-objective optimal algorithm has been run six times, a set of parameters are obtained, as shown in Figures 1(a)-(d). Figure 1(e) and Figure 1(f) show the change of fIAEm1 and fIAEm2 in each scenario, respectively.
Figure 1. The optimal results of NSGA-II for ADRC scheme. (a) The ADRC parameters in Tgas loop; (b) the ADRC parameters in Pgas loop; (c) the ADRC parameters in CVgas loop; (d) the ADRC parameters in Mass loop; (e) the values 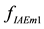
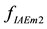
Although the scope of the Y-axis the change of the RIAE indices of the CVgas in Figure 1(e) is irregular. The values fIAEm2 arrive at their biggest values in the fifth scenario corresponding to add sine disturbance to the gasifier at 0% load. The solution with the biggest the coal quality flexibility 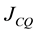
The comparisons of the twelve objective functions and the total RIAE indices among Simm, ADRC2 and MOADRC are listed in Table 3 and Table 4, respectively. Table 3 and Table 4 show that the values of the objective functions and the total RIAE indices of the ADRC2 and MOADRC are superior to the that of Simm’s.
3.3. Performance Tests
With the parameter set MOADRC, the performance tests of ADRC scheme are done. The simulation results are compared with that of Simm’s, MOPI2 and ADRC2.
Performance Tests
(1) Psink disturbance tests
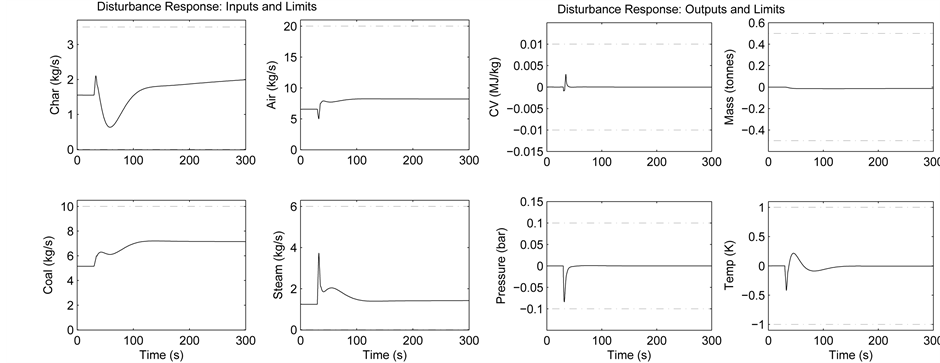
Based on the specification of the ALSTOM gasifier [2] , when the sine and step disturbances are added to the gasifier, respectively, the change of the corresponding indices are observed. All results of pressure disturbances can satisfy the requirements of the performance tests. Figure 2 and Figure 3 show the response graphs with step
Table 2. Comparison the ADRC2 with MOADRC.
Table 3. Comparisons objective functions among Simm, ADRC2 and MOADRC.
Table 4. Comparisons sum of RIAE among Simm, ADRC2 and MOADRC.
Figure 2. Response to step disturbance at 0% load.
Figure 3. Response to sine disturbance at 0% load.
and sine disturbances at 0% load. The simulation results at 100% and 50% loads are omitted.
(2) Load change test
Load change test of MOADRC are shown in Figure 4, the comparisons of simulation results obtained from the four sets of parameters are shown in Table 5. The simulation results of the ADRC2 and MOADRC in Table 5 show that the output temperature has almost no overshoot, and that the values of BM_min, BM_end and TPV_coal have a slight difference.
(3) Coal quality change test
In this test, when the coal quality is changed incrementally (within the range ±18%) with step or sine disturbance at certain load, upper and lower boundary guaranteeing the gasifier in steady state are recorded. The simulation results are shown in Table 6. The coal quality flexibility JCQ based on the formula (3) are calculated and shown in Table 7. The parameter set MOADRC have the biggest coal quality flexibility than other parameter families.
4. Conclusion
In this study, NSGA-II is introduced to choose the set of control parameters for ADRC scheme of the ALSTOM gasifier. Simulation results with the optimized parameters show that load change and coal quality change achieve relative good dynamics responses, larger scales of rejecting coal quality disturbances. The study also provides an alternative to choose parameters for other control schemes of the ALSTOM gasifier.

Figure 4. Response to the load change test. (a) Inputs response to load change; (b) outputs response to load change.
Table 5. Comparisons of the indices in load change test.
Table 6. Comparison of the rejection the coal quality change.
Table 7. Comparison of coal quality flexibility JCQ.
Fund
This project is supported by the Science & Technology Program of Beijing Municipal Commission of Education (KM201511417012).
Cite this paper
Chun’eHuang,ZhongliLiu, (2015) Multi-Objective Optimization for Active Disturbance Rejection Control for the ALSTOM Benchmark Problem. International Journal of Clean Coal and Energy,04,61-68. doi: 10.4236/ijcce.2015.43006
References
- 1. Dixon, R., Pike, A.W. and Donne, M.S. (2000) The ALSTOM Benchmark Challenge on Gasifier Control. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 214, 389-394. http://dx.doi.org/10.1243/0959651001540744
- 2. Dixon, R. and Pike, A.W. (2004) Introduction to the 2nd ALSTOM Benchmark Challenge on Gasifier Control. In Control, ID255.
- 3. Dixon, R. (2005) Benchmark Challenge at Control 2004. Comput. Control Eng. IEE, 10, 21-23.
- 4. Asmar, B.N., Jones, W.E. and Wilson, J.A. (2000) A Process Engineering Approach to the ALSTOM Gasifier Problem. Proceedings of the Institution of Mechanical Engineers, 214, 441-452. http://dx.doi.org/10.1177/095965180021400601
- 5. Chin, C.S. and Munro, N. (2003) Control of the ALSTOM Gasifier Benchmark Problem Using H2 Methodology. Journal of Process Control, 13, 759-768. http://dx.doi.org/10.1016/S0959-1524(03)00008-8
- 6. Gatley, S.L., Bates, D.G. and Postlethwaite, I. (2004) H-Infinity Control and Anti-Windup Compensation of the Nonlinear ALSTOM Gasifier Model. In Control, ID 254.
- 7. Farag, A. and Werner, H. (2006) Structure Selection and Tuning of Multi-Variable PID Controllers for an Industrial Benchmark Problem. IEE Proceedings Control Theory and Applications, 153, 262-267. http://dx.doi.org/10.1049/ip-cta:20050061
- 8. Al Seyab, R.K., Cao, Y. and Yang, S.H. (2006) Predictive Control for the ALSTOM Gasifier Problem. IEE Proceedings Control Theory and Applications, 153, 293-301.
- 9. Taylor, C.J. and Shaban, E.M. (2006) Multivariable Proportional-Integral-Plus (PIP) Control of the ALSTOM Nonlinear Gasifier Simulation. IEE Proceedings Control Theory and Applications, 153, 277-285. http://dx.doi.org/10.1049/ip-cta:20050058
- 10. Wilson, J.A., Chew, M. and Jones, W.E. (2006) State Estimation-Based Control of a Coal Gasifier. IEE Proceedings Control Theory and Applications, 153, 270-276. http://dx.doi.org/10.1049/ip-cta:20050071
- 11. Simm, A. and Liu, G.P. (2006) Improving the Performance of the ALSTOM Baseline Controller Using Multiobjective Optimization. IEE Proceedings Control Theory and Applications, 153, 286-292. http://dx.doi.org/10.1049/ip-cta:20050131
- 12. Xue, Y.L., Li, D.H. and Gao, F.R. (2010) Multi-Objective Optimization and Selection for the PI Control of ALSTOM Gasifier Problem. Control Engineering Practice, 18, 67-76. http://dx.doi.org/10.1016/j.conengprac.2009.09.004
- 13. Tan, W., Lou, G. and Liang, L. (2011) Partially Decentralized Control for ALSTOM Gasifier. ISA Transactions, 50, 397-408. http://dx.doi.org/10.1016/j.isatra.2011.01.008
- 14. Huang, C.-E., Li, D.H. and Xue, Y.L. (2013) Active-Disturbance-Rejection-Control for the ALSTOM Gasifier Bench- mark Problem. Control Engineering Practice, 21, 556-564. http://dx.doi.org/10.1016/j.conengprac.2012.11.014
- 15. Deb, K., Pratap, A., Agarwal, S. and Meyarival, T. (2002) A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6, 182-196. http://dx.doi.org/10.1109/4235.996017
NOTES
*Corresponding author.