American Journal of Climate Change
Vol.04 No.01(2015), Article ID:54360,7 pages
10.4236/ajcc.2015.41001
Rainy/Non-Rainy Day Pattern Analysis for North Carolina
Akand W. Islam
Bureau of Economic Geology, Austin, TX, USA
Email: awislam@utexas.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 February 2015; accepted 28 February 2015; published 3 March 2015
ABSTRACT
Trends in rainy/non-rainy days are investigated using the Mann-Kendall non-parametric test at 249 weather station sites of North Carolina, United States. Sen-Slope method has been applied to predict the trend magnitude. Inverse distance weighing interpolation technique is adopted to represent the spatial distribution of trend magnitude across the North Carolina. Quality controlled daily precipitation data sets from 1950 to 2009 have been used to analyze. The double-mass curve and autocorrelation were adopted to analyze the precipitation time series of each station to check the consistency and homogeneity. Standard Precipitation Index (SPI) has also been discussed for the study area. It is found in North Carolina that a number of rainy day trends are increasing both spatially and temporally. Eastern part of North Carolina shows the significant increasing rainy day trends. Trend significance has been checked at 1% and 5% significance level. Recent decades show the high SPI in both the extent of wetness and dryness.
Keywords:
Mann-Kendall, Sen-Slope, Inverse Distance Weighing Interpolation, Trend Significance

1. Introduction
Trends in precipitation have been observed for last one century in many parts of the globe. Over this period, precipitation increased significantly in eastern parts of North and South America [1] . Increasing intensity of precipitations in terms of number of rainy and/or non-rainy days is of great concern by the climate change researchers throughout the world. An increase in precipitation will lead to prolonged, either droughts or floods. Karl and Knight [2] showed statistically significant precipitation increase (greater than 50 mm per day) in the United States. Over the last several decades, the total precipitation has increased across the United States [3] [4] . Using Climate Division database, Keim and Fischer [5] found an increasing precipitation over time in the United States. Small et al. [4] found large increment of precipitation in the eastern United States. A recent study by Sayemuzzaman and Jha [6] shows the statewide increasing precipitation in North Carolina for all the seasons and annual time scale except winter. However, they have not shown the rainy/non-rainy day trend pattern as well the extent of precipitation in terms of Standard Precipitation Index (SPI).
This study analyzes the spatial and temporal rainy/non-rainy day trend in annual scale for North Carolina in the period of 1950-2009. The non-parametric Mann-Kendall (MK) test and Sen-Slope (SS) were applied to detect the trend significance and slope, respectively.
2. Data and Methodology
2.1. Regional Setting and Data Sets
This study is carried out for the state of North Carolina which is located in Eastern part of the United States (75˚30' - 84˚15'W, 34˚ - 36˚21'N) (see Figure 1), covers an area of approximately 136,399 km2. North Carolina exhibits one of the most complex climates in the United States for its variant topographic features that range from 46 m from the eastern coastal area to the western mountain area of 1829 m height [7] . The southwestern North Carolina is the rainiest in the eastern United States, receives 2286 mm of rainfall annually because southerly winds are forced upward in passing over the mountain barrier whereas less than 80 km from this region to the north, in the valley of the French Broad river, surrounded by mountain ranges on all sides, is the driest point south of Virginia and east of the Mississippi river [7] . These altitude variation features and anomalous precipitation in some portion across North Carolina produces zonal temperature trend variations [8] .
Precipitation from the 249 stations across North Carolina was analyzed for the period of 1950-2009. The data sets were obtained from the United States Department of Agriculture-Agriculture Research Service (USDA- ARS) [9] , which were originally facilitated by National Oceanic and Atmospheric Administration (NOAA). Daily values were averaged to obtain annual precipitation for each of the 249 stations. The double-mass curve and autocorrelation was adopted to analyze the precipitation time series of each station to check the consistency and homogeneity [10] . Double-mass curve analysis is a graphical method for checking consistency of a hydrological record. It is considered to be an essential tool before taking it for further analysis. Inconsistencies in hydrological or meteorological data recording may occur due to various reasons, such as: changes in observation procedures, instrumentation, or changes in gauge location or surrounding conditions [11] .
Surface interpolation technique was used to prepare a spatial precipitation data map over North Carolina from the point precipitation measuring stations within the Arc-GIS framework, which was adopted in Sayemuzzaman and Jha’s investigations [12] . For spatial distribution of trends in maps, contours are generated using an Inverse-Distance-Weighted (IDW) algorithm with a power of 2.0, 12 grid points and variable radius location.
2.2. Methodology
2.2.1. Mann-Kendall (MK) Trend Test
The MK statistical test has been frequently used to quantify the significance of trends in hydro-meteorological time series [10] [13] [14] . Original model was developed by Mann [15] , and after that Kendall [16] derived the test statistic distribution. The MK test statistic S [15] [16] is calculated as
Figure 1. Distribution of precipitation stations (black circles) in North Carolina.
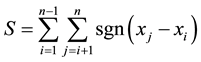 (1)
(1)
In Equation (1), n is the number of data points, 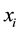 and
and  are the data values in time series i and j (j > i), respectively, and in Equation (2)
are the data values in time series i and j (j > i), respectively, and in Equation (2) 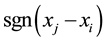 is the sign function as
is the sign function as
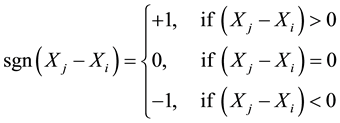 (2)
(2)
The variance is computed as
 (3)
(3)
In Equation (3), n is the number of data points, m is the number of tied groups and 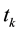 denotes the number of ties of extent k. A tied group is a set of sample data having the same value. In cases where the sample size n > 10, the standard normal test statistic
denotes the number of ties of extent k. A tied group is a set of sample data having the same value. In cases where the sample size n > 10, the standard normal test statistic 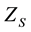 is computed using Equation (4):
is computed using Equation (4):
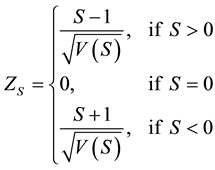 (4)
(4)
Positive and negative values of 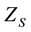 indicate increasing trends and decreasing trends, respectively. MK test was applied to detect, if a trend in the precipitation time series was statistically significant at the significance levels α = 0.01 (or 99% confidence intervals) and α = 0.05 (or 95% confidence intervals). At the 5% and 1% significance level, the null hypothesis of no trend is rejected if
indicate increasing trends and decreasing trends, respectively. MK test was applied to detect, if a trend in the precipitation time series was statistically significant at the significance levels α = 0.01 (or 99% confidence intervals) and α = 0.05 (or 95% confidence intervals). At the 5% and 1% significance level, the null hypothesis of no trend is rejected if 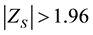 and
and , respectively.
, respectively.
2.2.2. Sen-Slope (SS)
The MK test does not provide an estimate of the magnitude of the trend. For this purpose in this study, a nonparametric method referred to as the Sen-Slope (SS) is used [17] . This approach provides a more robust slope estimate than the least-squares method because it is insensitive to outliers or extreme values and competes well against simple least squares even for normally distributed data in the time series [18] . This method has been widely used by the researchers for the trend magnitude prediction in hydro-meteorological time series [13] [19] - [21] . This study using the magnitude of the trend follows steps below.
i) The interval between time series data points should be equally spaced.
ii) Data should be sorted in ascending order according to time, then the following formula is applied to calculate Sen’s slope (Qk):
 (5)
(5)
In Equation (5), Xj and Xi are the data values at times j and i (j > i), respectively.
iii) In the Sen’s vector matrix members of size 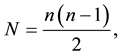 where n is the number of time periods. The
where n is the number of time periods. The
total N values of Qk are ranked from smallest to largest and the median of slope or Sen’s slope estimator is com- puted as:
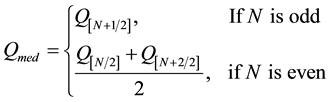 (6)
(6)
Qmed sign reflects data trend direction, while its value indicates the steepness of the trend.
2.2.3. Serial Correlation Effect
The steps adopted in the sample data 
1) The lag-1 serial coefficient 



where
2) According to Gocicand Trajkovic [13] and most recent studies [10] [19] the following equation for

testing the time series data sets of serial correlation have been used.
If 

3) If time series data sets are independent, then the MK test and the SS can be applied to original values of time series.
4) If time series data sets are serially correlated, then the “Pre-whitened” time series may be obtained as 
3. Results and Discussions
3.1. Precipitation Time Series
Figure 2 shows the daily time series precipitation from Jan 1, 1950 to Dec 31, 2009. Small linear increasing trend (+0.000002 mm/day) was noticed during this entire time period. Maximum daily precipitation 80.5 mm was recorded in September 16, 1999. That was because of the post-flooding effect. Mean and median of daily precipitation was found 3.45 mm/day and 0.97 mm/day, respectively. Ups and downs precipitation values
Figure 2. Time series of daily precipitation.
represent the seasonal effect. It is seen from this daily time series data North Carolina does not represent high variability/abnormality in precipitations.
3.2. Rainy and No-Rainy Day Trends
Figure 3 illustrates the spatial distribution of rainy day trends in terms of significance and magnitude (days/year) across the North Carolina. Rainy day increasing trends are higher than the decreasing trends at 1% significance level, and are distributed across North Carolina. Most of the western part and coastal region at the eastern part of North Carolina exhibits the significant (1% significance level) increasing trends. One of the biggest cities in North Carolina, Charlotte in Mecklenburg county, situated south-east part of the piedmont region, show number of rainy day increasing trends over 60 years period. Overall rainy day trends are increasing in North Carolina. Figure 4 represents the non-rainy day trends, mixed (decreasing-increasing) trends and equal spatial significant trend distribution were noticed.
Figure 5 shows the temporal rainy/non-rainy day trend of average over all the 249 weather station data in annual scale. It is also obvious in temporal pattern over 60 years average data that rainy day (non-rainy day) trend is increasing (decreasing). Temporal trend magnitude for rainy day +0.22 day/year and for non-rainy day −0.21 day/year is found.
3.3. Standard Precipitation Index (SPI)
The Standardized Precipitation Index (SPI), developed by [24] , is based only on precipitation. The SPI is the number of standard deviations that the observed value would deviate from the long-term mean. One unique feature is that the SPI can be used to monitor conditions on a variety of time scales. This temporal flexibility allows the SPI to be useful in both short-term agricultural and long-term hydrological applications. In this study the
Figure 3. Spatial distribution of rainy day trends in terms of significance and magnitude (days/year).
Figure 4. Spatial distribution of non-rainy day trends in terms of significance and magnitude (days/year).
annual SPI for 249 stations was averaged and represented from 1950 to 2009 in Figure 6. Positive (negative) values of SPI represent the extent of wetness (dryness) pattern of precipitation. SPI index found was greater than 1.5 (extremely wet) and smaller than −1.5 (extremely dry) around after 1980. SPI close to +2.0 and −2.0 was found in last decade.
4. Conclusion
Trends in rainy/non-rainy days have been investigated using the Mann-Kendall and Sen-Slope non-parametric methods at 249 weather station sites of North Carolina, United States. Inverse distance weighing interpolation technique is adopted to represent the spatial distribution of trend magnitude. Quality controlled daily precipitation data sets from 1950 to 2009 have been used in this study. The double-mass curve and autocorrelation were adopted to analyze the precipitation time series of each station to check the consistency and homogeneity. Standard Precipitation Index (SPI) has also been discussed for the study area. It is found in North Carolina that a number of rainy day trends are increasing both spatially and temporally. Eastern part of North Carolina shows the significant increasing rainy day trends. Trend significance has been checked at 1% and 5% significance level. Recent decades show the high SPI in both the extent of wetness and dryness.
Figure 5. Rainy/non-rainy day temporal trends.
Figure 6. 12 months Standard Precipitation Index (SPI).
Acknowledgements
The author acknowledges Dr. Sayemuzzaman, Florida State University, for constructive comments, data collection and analyses.
References
- GIPCC (2007) Climate Change 2007: The Physical Science Basis, Summary for Policymakers. In: Solomon, S., et al., Eds., Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC), Cambridge Univ Press, Cambridge, 237-336.
- Karl, T.R. and Knight, R.W. (1998) Secular Trends of Precipitation Amount, Frequency, and Intensity in the United States. Bulletin of the American Meteorological Society, 79, 231-241. http://dx.doi.org/10.1175/1520-0477(1998)079<0231:STOPAF>2.0.CO;2
- Kunkel, K., Andsager, K., Liang, X., Arritt, R., Takle, E., Gutowski, W. and Pan, Z. (2002) Observations and Regional Climate Model Simulations of Heavy Precipitation Events and Seasonal Anomalies: A Comparison. Journal of Hydrometeorology, 3, 322-334. http://dx.doi.org/10.1175/1525-7541(2002)003<0322:OARCMS>2.0.CO;2
- Small, D., Islam, S. and Vogel, R.M. (2006) Trends in Precipitation and Streamflow in the Eastern US. Paradox or Perception? Geophysical Research Letters, 33, Article ID: L03403. http://dx.doi.org/10.1029/2005GL024995
- Keim, B.D. and Fischer, M.R. (2005) Are There Spurious Precipitation Trends in the United States Climate Division Database? Geophysical Research Letters, 32, Article ID: L04702. http://dx.doi.org/10.1029/2004GL021985
- Sayemuzzaman, M. and Jha, M. (2014) Seasonal and Annual Precipitation Time Series Trend Analysis in North Carolina, United States. Atmospheric Research, 137, 183-194. http://dx.doi.org/10.1016/j.atmosres.2013.10.012
- Robinson, P. (2005) North Carolina Weather and Climate. University of North Carolina Press in Association with the State Climate Office of North Carolina. Ryan Boyles, Graphics.
- GorjiSefidmazgi, M., Sayemuzzaman, M., Homaifar, A., Jha, M.K. and Liess, S. (2014) Trend Analysis Using Non- Stationary Time Series Clustering Based on the Finite Element Method. Nonlinear Processes in Geophysics, 21, 605- 615. http://dx.doi.org/10.5194/npg-21-605-2014
- USDA-ARS (2014) Agricultural Research Service, United States Department of Agriculture. http://www.ars.usda.gov/Research/docs.htm?docid=19440
- Sayemuzzaman, M., Jha, M.K. and Mekonnen, A. (2014) Spatio-Temporal Long-Term (1950-2009) Temperature Trend Analysis in North Carolina, United States. Theoretical and Applied Climatology, 116, 3-4. http://dx.doi.org/10.1007/s00704-014-1147-6
- Peterson, T.C., Easterling, D.R., Karl, T.R., Groisman, P.Y., Nicholis, N., Plummer, N., Torok, S., Auer, I., Boehm, R., Gullett, D., Vincent, L., Heino, R., Tuomenvirta, H., Mestre, O., Szentimrey, T., Salinger, J., Førland, E., Hanssen- Bauer, I., Alexandersson, H., Jones, P. and Parker, D. (1998) Homogeneity Adjustments of in Situ Atmospheric Climate Data: A Review. International Journal of Climatology, 18, 1493-1517. http://dx.doi.org/10.1002/(SICI)1097-0088(19981115)18:13<1493::AID-JOC329>3.0.CO;2-T
- Sayemuzzaman, M. and Jha, M.K. (2014) Modeling of Future Land Cover Land Use Change in North Carolina Using Markov Chain and Cellular Automata Model. American Journal of Engineering and Applied Science, 7, 295-306. http://dx.doi.org/10.3844/ajeassp.2014.295.306
- Gocic, M. and Trajkovic, S. (2013) Analysis of Changes in Meteorological Variables Using Mann-Kendall and Sen’s Slope Estimator Statistical Tests in Serbia. Global and Planetary Change, 100, 172-182. http://dx.doi.org/10.1016/j.gloplacha.2012.10.014
- Chang, S.Y. and Sayemuzzaman, M. (2014) Using Unscented Kalman Filter in Subsurface Contaminant Transport Models. Journal of Environmental Informatics, 23, 14-22. http://dx.doi.org/10.3808/jei.201400253
- Mann, H.B. (1945) Non-Parametric Tests against Trend. Econometrica, 13, 245-259. http://dx.doi.org/10.2307/1907187
- Kendall, M.G. (1975) Rank Correlation Measures. Charles Griffin, London.
- Sen, P.K. (1968) Estimates of the Regression Coefficient Based on Kendall’s Tau. Journal of the American Statistical Association, 63, 1379-1389. http://dx.doi.org/10.1080/01621459.1968.10480934
- Fan, J.Q. and Yao, Q.W. (2003) Nonlinear Time Series: Nonparametric and Parametric Methods (Springer Series in Statistics). Springer-Verlag, New York.
- Sayemuzzaman, M., Jha, M.K., Mekonnen, A. and Schimmel, K.A. (2014) Subseasonal Climate Variability for North Carolina, United States. Atmospheric Research, 145, 69-79. http://dx.doi.org/10.1016/j.atmosres.2014.03.032
- Sayemuzzaman, M. (2010) Using Unscented Kalman Filter in Subsurface Contaminant Transport Models. Master’s Thesis, Energy and Environmental System Department, North Carolina A & T State University, Greensboro.
- Sayemuzzaman, M. and Jha, M.K. (2013) Monthly Time Series Trend Analysis of Temperature and Precipitation in North Carolina. Proceedings of the AGU Fall Meeting, San Francisco, 9-13 December 2013, 1-8.
- Salas, J.D., Delleur, J.W., Yevjevich, V.M. and Lane, W.L. (1980) Applied Modeling of Hydrologic Time Series. Water Resources Publications, Littleton.
- Sayemuzzaman, M. (2014) Spatio-Temporal Trends of Climate Variability in North Carolina. Ph.D. Dissertation, North Carolina A & T State University, Greensboro.
- McKee, T.B., Nolan, J.D. and Kliest, J. (1993) The Relationship of Drought Frequency and Duration of Time Scales. Proceedings of the 8th Conference on Applied Climatology, Anaheim, 17-22 January 1993, 1-6.







