American Journal of Climate Change
Vol.03 No.05(2014), Article ID:52625,7 pages
10.4236/ajcc.2014.35037
Assessment of Ice Volume Changes in the Cryosphere via Simplified Heat Transport Model
T. V. Hromadka II1, H. D. McInvale1, M. Phillips1, B. Espinosa2
1Department of Mathematical Sciences, United States Military Academy, West Point, New York, USA
2Hromadka & Associates, Rancho Santa Margarita, CA, USA
Email: tedhromadka@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 September 2014; revised 21 October 2014; accepted 6 November 2014
ABSTRACT
In order to describe changes in ice volume in the cryosphere, a differential equation mathematical model is used in this paper. The dominating effects of freezing and thawing in the cryosphere enable simplification of the heat transport equations. This results in a mathematical model that can be solved exactly and is useful in investigating other climatic components, which in turn may be similarly analyzed for possible Global Circulation Model (GCM) validation. Data forms represent- ing temperature and ice volume during the Pleistocene are available and can be directly compared with the exact solution of the simplified differential equation used in this paper. The model parameters may then be adjusted to approximate the effects of climate change; the adjusted model then run in reverse time, to develop an alternative history of ice volume of the cryosphere to be compared with the actual data interpretations previously published in the literature. In this fashion, an assessment may be made as to possible climate impacts in the cryosphere.
Keywords:
Global Climate Change, Cryosphere, Phase Change, Cumulative Departure Method

1. Introduction
The use of Global Climate Models (or Global Circulation Models, GCMs) appears to be becoming a main stream course in the analysis of climate change effects in order to develop public policy, despite the mixed reactions documented in recent literature regarding the success of their use (e.g., [1] -[3] ). The trend towards the inclusion of additional components of the heat budget and its several transport mechanisms in GCM model development has highlighted the need to better address uncertainty problems, as shown in the focused modeling efforts of some individual transport mechanisms (for example, see [4] ). There are, however, some aspects of the climate which, depending on the time scale involved and the primary heat budget elements may be more predictable. For example, some efforts such as [3] [5] [6] suggest that due to the dominating effects of the latent heat of phase change in freezing and thawing, a model of the heat budget associated with the cyrosphere may be more tractable. In this paper, model parameters from a differential equation based solution representing temperature and ice volume during the Pleistocene are used to approximate effects of climate change.
2. Mathematical Model
The proposed conceptual model will directly relate estimates of temperature found in the literature (as derived from proxy data, such as the ratio dD; for example, see [7] -[13] ) to estimates of ice volume (as derived from proxy data, such as the ratio d18O; see [7] [8] [14] ). Similar to the underpinnings of the Stefan model (e.g., [15] ) for freezing and thawing soils or other medium, the heat budget relationship can be simplified due to the dominating effects of freezing and thawing of water in thecryosphere. From the resulting mathematical analog of temperature and ice volume, an exact solution is obtained. Model calibration is achieved with normalized data of frozen material, I(t), for the Pleistocene time period. To simplify the calibration process, the governing differential equation is normalized to reduce the number of parameters.
The heat transport effects that impact the problem domain include solar and internal heat within the planet, circulation of the atmosphere and oceans with corresponding interface and convective heat transport effects, among others. All of these components interface and integrate together and are represented by the term [Heat] . (The notation [Heat] includes all the components of heat transport that effect phase change in the cryosphere. The total heat budget can be found in [16] , among others.) [Heat] includes all the thermal balance elements of the heat budget, with magnitude, H(t). The function H(t) is determined by calibration to the historic temperature T(t) function developed from historic data. In the current approach, H(t) is developed by examining what H(t) did in the past with respect the T(t) function. This modeling approach of building H(t) based upon what H(t) did in the past may sidestep many complexities that are involved in assembling approximations of the various sub- processes and feedbacks that form the climate and associated boundary conditions. Furthermore, such an H(t) can still be modified to represent changes in the environment.
3. Data and Use of Proxy Relationships
Details regarding conceptual model parameters, data types used and corresponding proxy relationships are presented in [4] but are summarized here for the reader’s convenience. The solution to the initial basic conceptual model relates an input forcing function, H(t), to the output I(t) function. The input function is assumed to follow the trends of reported data, such as ice core temperature estimates ([8] [13] [17] ). Under assumed “natural conditions”, the output function, I(t) , is assumed to also follow the data trends that relate frozen material measure to proxy data such as d18O.
Because normalized data are used, the forcing function, H(t), is linearly related to the selected temperature data proxy for the time domain of interest. That is, for some constants a1 and a2, and assuming H(t) = a1 + a2T(t), then when transformed into normalized N(0,1) form, both functions H(t) and T(t) plot identically. Consequently, one can work directly with the N(0,1) normalized form of a selected T(t) realization. Furthermore, the estimated temperature T(t) is typically given as a linear function of the proxy data, dD (for example, see [7] -[11] , among others). Consequently, the model formulation necessarily is using a linear transform of dD as the forcing function, and therefore the N(0,1) transform of the available dD source data serves to describe the forcing function.
Some papers suggest that ice volume estimates may be written as a linear function of d18O (e.g., [7] [8] [18] ) and other papers suggest that ice volume estimates may be developed using a nonlinear function of d18O (e.g., [19] ). Assuming that the relationship is linear for the range of conditions contemplated in the modeling formulation, the N(0,1) transform of the available d18O source data describes the ice volume trends during the Pleistocene time period. (If the relationship is nonlinear, then the N(0,1) transform of the d18O source data may require further considerations such as including other statistical moments or using another choice of transformation.) In the current paper, d18O data [20] [21] is used as a proxy for representing the trends of ice volume.
The general solution to the conceptual model operates upon estimates of the magnitude of heat, H(t) , assumed to be a linear function of temperature. In turn, these are assumed to be a linear function of dD and produce an output of ice measure that is calibrated to estimates of ice volume. Ice volume is assumed to be a linear function of d18O (as stated previously, the above development can consider a nonlinear transformation of d18O, or other proxy data). Hence, the model solution is a mapping (i.e., a relationship between the two measured variables considered) from dD to d180.
The proxy data types considered in this paper include those listed in Table 1. Each type of proxy shown in bold in Table 2 was collected and processed by partitioning the study time domain into 1000-year intervals (the selection of a 1000-year partition is consistent with the partition size used in [22] -[24] in a study of phase-space modeling for Pleistocene ice volume). The resulting partition was modified to better fit the source data relative to the maximum and minimum data in order to capture the respective peak and minimal values. The modified partitioned data were then transformed using the standard normal transformation N(0,1) transformation. In such a normalized form, calibration of the forcing function H(t) to a selected proxy and calibration of the governing PDE solution I(t) is made simpler as fewer parameters are involved.
4. Mathematical Analog
In [4] (Equation (1) and following), a mathematical analog of changes in volumetric ice in the cryosphere is developed given by,
 (1)
(1)
where
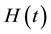 = total heat into the system affecting phase change in the cryosphere;
= total heat into the system affecting phase change in the cryosphere;
 = total volumetric ice in the cryosphere including glaciers, tundra ice, snow and other forms of water subject to freeze/thaw effects;
= total volumetric ice in the cryosphere including glaciers, tundra ice, snow and other forms of water subject to freeze/thaw effects;
 = an initial condition of
= an initial condition of , contemplated as a local maximum value such as during a glacial period;
, contemplated as a local maximum value such as during a glacial period;
 = lumped parameter representing that portion of heat returned due to phase change effects, such as reflected heat due to snow, among other factors, where
= lumped parameter representing that portion of heat returned due to phase change effects, such as reflected heat due to snow, among other factors, where ;
;
 = lumped parameter representing the area-averaged latent heat of fusion as averaged throughout the
= lumped parameter representing the area-averaged latent heat of fusion as averaged throughout the
Table 1. Proxy types.
Table 2. Climate change definitions.
cryosphere; and
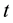 = model time.
= model time.
For details regarding the underpinnings of Equation (1), the reader is referred to [4] .
The ratio 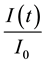 in Equation (1) represents the impact of changing geometry during phase change effects,
in Equation (1) represents the impact of changing geometry during phase change effects,
such as growing glaciers, or changing boundary lengths with respect to interface with ocean currents, among other effects.
It is straightforward to extend 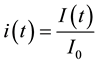 with an exponent, p, such that
with an exponent, p, such that 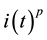 is considered in Equation (1). For the current work, however,
is considered in Equation (1). For the current work, however,  is retained.
is retained.
Dividing 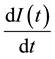 by model initial condition,
by model initial condition, 

where the initial condition for




Multiplying by


or

where G(t) is the total heat applied to the cryosphere between model times s = 0 and s = t (see [4] ).
5. Cumulative Departure Model (CDM)
Various fields of geoscience utilize the Cumulative Departure Model (CDM) when looking at long term trends in data where the data under examination (usually annual data) must be considered in the context of previous data influences (for example, groundwater accumulation with respect to annual rainfall). As such, the CDM method involves three steps: 1) calculate the mean for the complete data set; 2) subtract the mean from each data point to determine its relationship or departure from the mean (i.e., surplus or deficit); and 3) add the departures together to create a cumulative departure at each time step. In Equation (4), the second exponential term, G(t), indicates a long term trend of aggradation or degradation of



where 

Carrying forward the formulation of Equation (5) (indicating no long term aggradation or degradation of


where 

It is this formulation that is used to approximate climate change impacts upon our cryosphere based upon the above simplified mathematical model.
6. Modeling Effects on the Cryosphere from Climate Change
An opportunity is afforded, in assessing climate change impacts on the cryosphere, by using the simplified modeling equation formulation of Equations (6) through (8). Specifically, the key model D parameter of Equation (8) is a composite of five parameters which results in the variation in the diffusion parameters analogous to the variation in the components of the parameter cluster. For example, a climate change impact that has the effect of increasing the area averaged latent heat of fusion parameter would be represented by a change in the “r” parameter, which inversely impacts the D parameter. Other such influences follow accordingly.
To assess the impact from such parameter changes, the D parameter is varied by 5%, 10% and 25%. The model of (6) through (8) is then run in reverse time for 435,000 years. Plots of the revised volumetric ice contents versus time (expressed in years before present time) are shown in Figures 1-3.
7. Discussion
From Figures 1-3, the simplified mathematical model formulation simulation results indicate that for changes in the D model parameter of 5% primarily shows more thawing of the cryosphere occurring during interglacials but
Figure 1. Modeling results with 5% variance of D.
Figure 2. Modeling results with 10% variance of D.
Figure 3. Modeling results with 25% variance of D.
that recovery substantially occurs during the next freeze cycle. However, at a 25% variation in the D parameter, significant impacts are indicated in the cryosphere ice volume. Even a 10% variation in D indicates significant change in volumetric ice content predictions.
From Equation (8), a variation in D is achieved by variation of several heat budget parameters or a larger variation by only one. For example, changes in the climate due to increased retention of heat, such as contemplated in some climate change model scenarios by others, can be approximately modeled by a decrease in the model return heat parameter, k. From Equation (8), increasing k implies decreasing values of D. Figures 1-3 demonstrate this simplified model estimate of the effect of both increased and decreased values of the D parameter.
From the figures, even for a 5% parameter variation in D, the indicated minimum volumetric ice content is seen to be substantially lower when compared with respect to the recent experience of volumetric ice content. That is, compared to recent measures, which are occurring during a thaw cycle, the predicted ice quantities would be significantly less. However, the next freezing cycle recovers the ice volume substantially. In contrast, a 25% variation in D indicates a far more substantial impact for both the thawing and freezing cycles. It is noted that in all of these simulations, the entire freeze/thaw records of several hundred thousand years is simulated. Simulating only a portion of the record would indicate less modeling impacts.
8. Conclusion
In this paper, the simple heat budget model formulated in [4] is used to develop estimates of cryosphere ice volume impacts due to small changes in modeling parameters caused by hypothesized climate change effects. The resulting mathematical model is a differential equation that can be solved exactly. The mathematical solution to the heat budget model is shown to be a two-parameter model that can be simplified further into a single parameter cluster, D, which is the product and quotients of the several heat budget parameters. Variations in a heat budget parameter result in a similar variation in the single parameter cluster, D. The mathematical model is shown to be an application of the Cumulative Departure Method used in other fields of geoscience. For the problems considered in this paper, computational power needed is provided by a spreadsheet program. Three scenarios of heat parameter effects are considered, of 5%, 10% and 25% variation. The 5% and even the 10% parameter variations indicate significant impacts to the cryosphere ice volume during thaw periods, but it is indicated that these impacts are partially explained by the smaller amounts of ice volume involved in the cryosphere.
Acknowledgements
Acknowledgements are paid to the United States Military Academy, West Point, NY, Department of Mathematical Sciences, for their support to the authors during this research. Also acknowledged are the several individuals who have participated in particular tasks in developing this paper including but by no means limited to Rene Perez, Laura Hromadka, Michael Barton, T.V. Hromadka III, among others.
References
- Randall, D.A., Wood, R.A., Bony, S., Colman, R., Fichefet, T., Fyfe, J., Kattsov, V., Pitman, A., Shukla, J., Srinivasan, J., Stouffer, R.J., Sumi, A. and Taylor, K.E. (2007) Climate Models and Their Evaluation. In: Climate Change 2007: The Physical Science Basis, Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
- Anagnostopoulos, G.G., Koutsoyiannia, D., Christofides, A., Efstratiadis, A. and Mamassis, N. (2010) A Comparison of Local and Aggregated Climate Model Outputs with Observed Data. Hydrological Sciences Journal, 55, 1094-1110. http://dx.doi.org/10.1080/02626667.2010.513518
- Bounoua, L., Hall, F.G., Sellars, P.J., Kumar, A., Collatz, G.J., Tucker, C.J. and Imhoff, M.L. (2010) Quantifying the Negative Feedback of Vegetation to Greenhouse Warming: A Modeling Approach. Geophysical Research Letters, 37, L23701. http://dx.doi.org/10.1029/2010GL045338
- Hromadka II, T.V., McInvale, H.D., Gatzke, B., Phillips, M. and Espinosa, B., (2014) Cumulative Departure Model of the Cryosphere during the Pleistocene. ASCE Journal of Cold Regions Engineering, 28. http://dx.doi.org/10.1061/(ASCE)CR.1943-5495.0000071
- Dyurgerov, M.B. and Meier, M.F. (1999) Twentieth Century Climate Change: Evidence from Small Glaciers. INSTAAR, University of Colorado at Boulder, Colorado (2005), Paper No.58, Institute of Arctic and Alpine Research.
- Bamber, J.L. and Payne, A.J. (2004) Mass Balance of the Cryosphere. Cambridge University Press, Cambridge, 145. http://dx.doi.org/10.1017/CBO9780511535659
- Petit, J.R., Jouzel, J., Raynaud, D., Barkov, N.I., Barnola, J.M., Basile, I., Bender, M., Chappellaz, J., Davis, J., Delaygue, G., Delmotte, M., Kotlyakov, V.M., Legrand, M., Lipenkov, V., Lorius, C., Pépin, L., Ritz, C., Saltzman, E. and Stievenard, M. (1999) Climate and Atmospheric History of the Past 420,000 Years from the Vostok Ice Core, Antarctica. Nature, 399, 429-436. http://dx.doi.org/10.1038/20859
- Petit, J.R., et al. (2001) Vostok Ice Core Data for 420,000 Years, IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series #2001-076. NOAA/NGDC Paleoclimatology Program, Boulder CO, USA.
- Jouzel, J., Lorius, C., Petit, J.R., Genthon, C., Barkov, N.I., Kotlyakov, V.M. and Petrov, V.M. (1987) Vostok Ice Core: A Continuous Isotope Temperature Record over the Last Climatic Cycle (160,000 Years). Nature, 329, 403-408. http://dx.doi.org/10.1038/329403a0
- Jouzel, J., Barkov, N.I., Barnola, J.M., Bender, M., Chappellaz, J., Genthon, C., Kotlyakov, V.M., Lipenkov, V., Lorius, C., Petit, J.R., Raynaud, D., Raisbeck, G., Ritz, C., Sowers, T., Stievenard, M., Yiou, F. and Yiou, P. (1993) Extending the Vostok Ice-Core Record of Palaeoclimate to the Penultimate Glacial Period. Nature, 364, 407-412. http://dx.doi.org/10.1038/364407a0
- Jouzel, J., Waelbroeck, C., Malaize, B., Bender, M., Petit, J.R., Stievenard, M., Barkov, N.I., Barnola, J.M., King, T., Kotlyakov, V.M., Lipenkov, V., Lorius, C., Raynaud, D., Ritz, C. and Sowers, T. (1996) Climatic Interpretation of the Recently Extended Vostok Ice Records. Climate Dynamics, 12, 513-521. http://dx.doi.org/10.1007/BF00207935
- Jouzel, J., Masson-Delmotte, V., Cattani, O., Dreyfus, G., Falourd, S., Hoffmann, G., Minster, B., Nouet, J., Barnola, J.M., Chappellaz, J., Fischer, H., Gallet, J.C., Johnsen, S., Leuenberger, M., Loulergue, L., Luethi, D., Oerter, H., Parrenin, F., Raisbeck, G., Raynaud, D., Schilt, A., Schwander, J., Selmo, E., Souchez, R., Spahni, R., Stauffer, B., Steffensen, J.P., Stenni, B., Stocker, T.F., Tison, J.L., Werner, M. and Wolff, E.W. (2007) Orbital and Millennial Antarctic Climate Variability over the Past 800,000 Years. Science, 317, 793-797. http://dx.doi.org/10.1126/science.1141038
- Jouzel, J. and Masson-Delmotte, V. (2007) EPICA Dome C Ice Core 800KYr Deuterium Data and Temperature Estimates. IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series # 2007-091. NOAA/NCDC Paleoclimatology Program, Boulder CO, USA.
- Lisiecki, L. and Raymo, M. (2005) A Pliocene-Pleistocene Stack of 57 Globally Distributed Benthic δ18O Records. Paleoceanography, 20, PA1003.
- Alexiades, V. and Solomon, A.D. (1993) Mathematical Modeling of Melting and Freezing Processes. Chapter 2. Problems with Explicit Solutions. Hemisphere Publishing Corporation, Washington, 33-124.
- Bitz, C.M. and Marshall, S.J. (2012) Encyclopedia of Sustainability Science and Technology. Springer Reference, Section on Climate Change Modeling and Methodology, 2761.
- Kawamura, K., et al. (2007) Dome Fuji Ice Core Preliminary Temperature Reconstruction, 0-340 kyr. IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series # 2007-074. NOAA/NCDC Paleoclimatology Program, Boulder.
- Zachos, J., Pagani, M., Sloan, L., Thomas, E. and Billups, K. (2001) Trends, Rhythms, and Aberrations in Global Climate Change 65 Ma to Present. Science, 292, 686-693. http://dx.doi.org/10.1126/science.1059412
- Mix, A.C. and Ruddiman, W.F. (1984) Oxygen-Isotope Analyses and Pleistocene Ice Volumes. Quaternary Research, 21, 1-20.
- Ruddiman, W.F. (2001) Earth’s Climate: Past and Future. W.H. Freeman & Sons, New York.
- Kawamura, K., et al. (2007) Dome Fuji Ice Core 340KYr (2500m) δ18O Data. IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series # 2007-074. NOAA/NCDC Paleoclimatology Program, Boulder.
- Imbrie, J. and Imbrie, J.Z. (1980) Modeling the Climatic Response to Orbital Variations. Science, 207, 943-953. http://dx.doi.org/10.1126/science.207.4434.943
- Imbrie, J., Hays, J.D., Martinson, D.G., McIntyre, A., Mix, A.C., Morley, J.J., Pisias, N.G., Prell, W.L. and Shackleton, N.J. (1984) The Orbital Theory of Pleistocene Climate: Support from a Revised Chronology of the Marine δ18O Record. In: Berger, A., Ed., Milankovitch and Climate, Part 1, Springer, New York, 269-305.
- Imbrie, J.Z., Imbrie-Moore, A. and Lisiecki, L. (2011) A Phase-Space Model for Pleistocene Ice Volume. Earth and Planetary Science Letters, 307, 94-102.





