InfraMatics
Vol. 2 No. 2 (2013) , Article ID: 33802 , 23 pages DOI:10.4236/inframatics.2013.22002
On Infrasound Standards, Part 1: Time, Frequency, and Energy Scaling
Infrasound Laboratory, Hawaii Institute of Geophysics and Planetology, School of Ocean and Earth Science and Technology, University of Hawaii at Manoa, Honolulu, USA
Email: milton@isla.hawaii.edu
Copyright © 2013 Milton A. Garces. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 6, 2013; revised June 15, 2013; accepted June 24, 2013
Keywords: Infrasound; Standards; Meteor
ABSTRACT
A standardized, self-similar, multiresolution algorithm is developed for scaling infrasonic signal time, frequency, and power within the framework of fractional octave bands. This work extends accepted fractional octave band schemas to 0.001 Hz (1000 s periods) to facilitate the analysis of broadband signals as well as the deep acoustic-gravity and Lamb waves captured by the global infrasound network. The Infrasonic Energy, Nth Octave (INFERNO) multiresolution Energy Estimator is applied to computing the total acoustic energy of the Russian meteor signature recorded in the 45 mHz - 9 Hz frequency band by IMS array 131 KZ, Kazakhstan.
1. Overture
Infrasound is used to characterize manifold natural and anthropogenic sources, from tsunamigenesis in the mHz frequency range to wind turbines near the audio range. The spectrum of atmospheric waves propagating at infrasonic speeds can span over four orders of magnitude (2 mHz - 20 Hz), a decade broader than the audio range (20 Hz - 20 kHz). Signals can be nearly continuous or transitory, and their energy spectrum can vary by more than twelve orders of magnitude (120 dB). The spatial distribution of infrasonic sensing systems may vary from meters to kilometers. Due to these diverse spatial, temporal, spectral, and intensity scales, it can be challenging to process infrasonic signals using consistent, reproducible parameters.
This paper is an invitation to standardize infrasound metrics using historical and ongoing efforts by diverse communities as a compass, and an entreaty to extend familiar algorithms and accepted standards into a slightly different, more transportable framework. It proposes a scaling of time, frequency and amplitude that may permit comparative calibrations, data quality assessments, and tests on sensing systems, as well as the benchmarking and validation of propagation models, detection algorithms, and classification taxonomies. Although this work presupposes a familiarity with digital signal processing of waveform signatures and some intimacy with spectral analysis, it does not require expertise in infrasound. This paper should provide sufficient information to permit the computational implementation of the proposed methodology and algorithms for further evaluation and improvement.
2. Infrasonic Pressure Signatures
Most infrasound data in the 21st century consists of 24- bit digital pressure waveforms with precise GPS time stamps, fixed station locations, and stable sampling rates. These data, with channel code BDF, are readily available through the IRIS DMC (http://www.iris.edu/dms/dmc/). A waveform associated with a source or event of interest is referred to as a signal. Its signature usually consists of the temporal, spectral, amplitude, and phase relationships that help identify the signal.
In general, we wish to detect, characterize, locate, and identify a signal of interest within an infrasonic pressure record. Yet these signals are often emergent, transient, immersed in ambient noise, and have distinguishing features that are not evident in raw pressure waveforms. In addition, a source signature can be significantly altered by atmospheric variability.
In practice, the first step in the inspection of a record is the assessment of waveform data quality and its statistical properties in the time domain. This step identifies data gaps, electronic noise, timing issues, clipping, or any other system problems that will degrade the usability of the data. If data are worthy of further processing, the next step in characterizing a signature is to compute its time-varying spectral amplitude. Figure 1 shows the broadband infrasonic signature of the Russian meteor captured by International Monitoring System (IMS) infrasound array I31KZ in Kazakhstan. This exploding fireball produced one of the most intense broadband signals captured by the IMS network, with sound radiated beyond the 4.5 mHz - 9 Hz passband shown in Figure 1. With properly scaled spectral parameters, the frequency domain representation is often more useful than the raw pressure record for identifying robust infrasonic signal features specific to an event of interest.
One of the keys in signal detection and identification is the ability to separate the signal spectrum from the noise spectrum, and eliminate as much of the noise as possible from subsequent analyses. A network of single microphones can readily identify energetic impulsive signals where the amplitude is much higher than the ambient noise within a given passband. By defining the total energy per frequency bin over the record duration in Figure 1 as the ambient intensity levels, it is possible to readily estimate a signal-to-noise (S/N) intensity ratio per timefrequency bin (Figure 2). A more sophisticated approach to estimating S/N is discussed in Section 7. However, a single sensor cannot differentiate between wind noise or competing acoustic sources, so the signal should be loud and clear for single-sensor or network processing.
At distances from tens to thousands of kilometers, or in situations where competing acoustic sources are present, more sophisticated systems are preferable. Four or more calibrated sensors precisely time-stamped and deployed as arrays can provide reliable signal detection within a designated frequency (f) band, or wavelength (l = cs/f) range, where cs is the (infrasonic, seismic, hydroacoustic, or gravity wave) signal speed at the array. An excellent review of array design criteria is given by [1]. A single array yields the direction of arrival (backazimuth) and the apparent signal velocity across the array aperture and can discriminate between dissimilar but simultaneous competing sources. With the notable exception of overhead regional sources, most infrasonic arrivals have an apparent acoustic signal speed close to that of the sound speed (c) at the array site. By using intersecting backazimuths, two properly sited arrays can locate and identify a source. Although infrasound arrays are used routinely by the international infrasound community for detection, location, and identification of natural and man-made events (e.g. [2]), there are no stan-
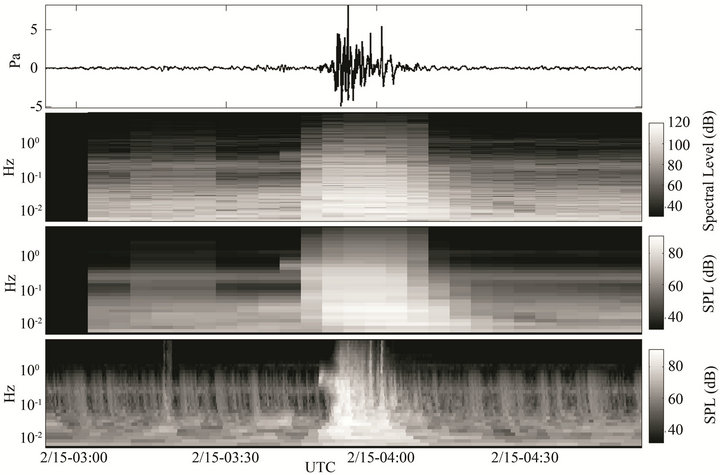
Figure 1. Russian meteor waveform and its spectral features at I31KZ observed on 15 February 2013 at a range of ~600 km from the source. This is one of the most broadband signals captured by the IMS network, and a bandwidth of 0.0045 Hz (4.5 mHz) to 9 Hz is shown in the logarthmic frequency axis. The upper panel is the bandpassed waveform, and the panel below it is the FFT spectrogram with a fixed time window duration (Equation (1)) and units of Pa2/Hz. The third panel from top is the sound pressure level (SPL) with the same time window as the spectrogram but in 1/3 octave bands. Since the FFT window duration is set by the lowest frequency, the temporal resolution is very coarse and there is substantial energy leakage between overlapped time windows, reducing signal onset precision. The lowermost panel is the SPL using the INFERNO multiresolution energy estimator described in Section 6, with a substantial increase in the accuracy and temporal resolution of the signal energy distribution.

Figure 2. Close up of beamformed waveform and its S/N ratio in dB relative to the averaged intensity over the record, without instrument correction.
dardized detection parameters for the validation and benchmarking of array processing algorithms.
To optimize array performance, the signal wavelength should be neither excessively large nor small relative to the array aperture L [3]. If the wavelength is too large, the errors in trace velocity and azimuth increase. If the wavelength is too small, we have spatial aliasing. For a typical four-element tripartite (centered triangle) array, the aperture can be approximately by the longest distance between elements, which is (generally) approximately twice the smallest inter-element distance. Aliasing would become prominent when l < L, but would be somewhat tolerable between the main lobe and the first grating lobe (L/2 < l < L). When l > L (with 12L as an empirical limit), oversampling [3] yields degraded precision in arrival azimuth and velocity estimates. In practice, we have much better performance than anticipated with high signal-to-noise (S/N) broadband transients, but if the S/N ratio decreases or the signal is more tonal one must be mindful of the reliability of array results. Taking L/2 < l < 12L as a practical array wavelength range leads to an array bandwidth of c/(12L) < f < c (2/L). Thus array I59US, Hawaii, with an aperture of 2 km, would have a bandwidth of [0.014 Hz - 0.34 Hz]. However,I59US routinely detects surf signals with a high S/N up to 4 Hz, with good performance at 1 Hz (l ~ L/6), where aliasing is predicted to be prominent but there is a decrease in ambient noise levels and a corresponding increase in S/N.
In contrast, array UH MENE in Volcano, Hawaii, with an aperture of 0.1 km, would have a detection bandwidth of [0.3 Hz - 6.8 Hz], yet also routinely detects signals well outside the band when the S/N is sufficiently high. Infrasound data for both I59US and MENE are available through the IRIS DMC. Note that a network can turn into an array if the frequency or propagation velocity are within the aforementioned optimal array bandwidth, for example when considering deep infrasound recorded by the IRIS US Array [4].
Array and network processing can separate signal from noise, although sometimes a signature is sufficiently distinct in amplitude and frequency to permit ready extraction with a single sensor. Signal detection parameters can be tuned to a known source signature, yet in exploratory research we don’t always have a priori knowledge of a signal’s signature and it is useful to have a robust, broadband detection parameter set that permits the identification of anomalous signals relative to an ambient sound field.
3. Conservation Principles
It is essential to identify parameters that can robustly and consistently characterize infrasonic signatures. Both continuous and transient signals and their combinations compose the ambient field, and should be considered.
In a linear acoustic system, the signal spectrum is preserved from source to the receiver, and no frequency component absent in the source can be observed at the receiver. However, Earth’s complex atmosphere and diverse topography conspire against linearity, which leaves the more interesting problem of quantifying how the source energy spectrum is repartitioned along the propagation path to the receiver. To consistently account for this energy repartitioning, it is useful to define a standardized set of frequency bins tuned to the signal of interest. The design of such frequency banks will be discussed in Section 5.
The conservation of apparent horizontal phase velocity, or ray parameter, during propagation in heterogeneous anisotropic atmospheres (e.g. [5,6]) is applicable for vertically stratified propagation environments. Most telesonic signals of interest arrive at the array with a nearlyhorizontal incidence angle, with an apparent velocity corresponding to the local sound speed at the receiver. The observed signal velocity across the array is valuable for identifying coherent signals and can be useful for the discrimination of overhead sources at close ranges. However, horizontal refraction near Earth’s surface, heterogeneities along the propagation path, multipathing, and simultaneous arrivals from competing sources can lead to low robustness in using the apparent horizontal phase velocity as an unambiguous arrival identifier. The apparent speed, or celerity, defined as the ratio of the total propagation range to the total travel time, was introduced in [7,8] as a more stable parameter for identifying multipath arrivals and locating telesonic ( >250 km) sources [9]. If the origin time and location of an event is well known, it is useful to plot the waveform celerity along the time axis for phase identification [10]. Winds transverse to the propagation direction will introduce an angular deviation from the expected arrival azimuth, which is often estimated with ray tracing algorithms [5]. Observed azimuth deviations can vary substantially (up to ±15 degrees) due in large part to the variability of atmospheric winds.
Causality is a fundamental requirement, one of the primary discriminants for signal association, and the main reason why the celerity estimates are useful. A signal associated with an event must not arrive before its fastest predicted propagation time, and not much later than permitted by the slowest propagation speed along a prescribed path. One can readily estimate the expected arrival times by using a nominal celerity range of Cel ~ [0.21 - 0.34] km/s, with propagation times of TCel = R/Cel, where R is the range (km) of the great circle path from the source to the receiver. However, temporal correlation does not imply causation, and assuming a signal corresponds to a known source only because of its time of arrival will lead to an overabundance of false detections and misidentifications. Furthermore, reradiation of sound by topography and bathymetry presents a coupled wave problem that may shift the expected sound reception window earlier or later, depending on the final sourcereceiver path [11].
Substantial effort has also been placed on amplitude scaling relationships (e.g. [12]). Sach’s scaling [13] exemplifies a robust set of scaling relationships between source pressures, period, yield, and range representative of the hydrodynamics of explosive detonations, but should only be applied to the near-field regime and physical processes for which they were designed. Attempts have been made at deriving scaling laws using either peak overpressure or peak period applicable to distances extending well beyond the hydrodynamic regime where the Sach’s scaling is valid. However, due to nonlinearities inherent in finite amplitude effects at high altitudes, atmospheric attenuation, and scattering, neither peak period (frequency) or amplitude (overpressure) have a physical conservation law that justifies their preservation during telesonic propagation.
In summary, in infrasonic propagation the transfer function between the source and receiver is nonlinear and anisotropic. The source spectrum is not always preserved, the apparent horizontal velocity is not a reliable discriminant for infrasonic arrivals, azimuth deviations are temperamental, causality is essential but ambiguous, and existing scaling laws can be fickle. Conservation of momentum is already used in the governing acoustic-gravity wave equations, and the only remaining, reliably invariant principle is the conservation of energy, with the caveat that it is necessary to isolate the system in consideration. This could include, but not be limited to, geomagnetic perturbations, gravity wave fields, solar tides, severe weather disturbances, and wave coupling in Earth’s solids, liquids, gases, and plasmas, and combinations thereof.
The next sections focus on developing a standardized methods for estimating the energy, or intensity, of an observed infrasonic pressure signature with substantial energy below 20 Hz. Due to the aforementioned complications introduced by the source physics and propagation environment, it will be instructive to accurately track the changes in the statistical properties of a signal as a function of time and frequency as it travels across a network of sensors or arrays. These statistical properties provide a measure of the variability of the source processes and propagation media.
4. Scaling Time
Acoustics is a branch of fluid mechanics, where scaling and nondimensionalized numbers are routinely used to create numerical and laboratory models of complex fluid behavior. For systems with intrinsic characteristic frequencies, dimensions, speeds, or time constants, it is often possible to identify a flow regime for which these intrinsic values are interrelated. Self-similar relationships reproduce themselves at different scales in such a way that they replicate nondimensionalized attributes [14].
This section develops self-similar time window durations for processing and characterizing waveform data using pre-existing standards for reference and validation. Although this paper concentrates on infrasonic pressure in Pascals (Pa), the proposed methodology is transportable to other measurements amenable to Fourier synthesis, such as displacement, velocity and acceleration, or even counts in the absence of a calibration value. The primary scaling variables would be the effective array aperture L and either the lowest frequency (for Fourier synthesis) or the center frequencies (for filter banks)
within a prescribed signal bandwidth. In doing so, it is possible to extend the basic principles of Fourier synthesis to high-resolution multispectral analysis techniques in logarithmic-frequency space with time-window autoscaling.
Spectral decomposition using the Fast Fourier Transform (FFT) is routine in the acoustics community. Power spectral densities and spectrograms are commonly applied to sound records, with the probability density function of the power spectral density providing a useful measure of confidence levels. Not surprisingly, Fourier synthesis performs well on tones and harmonics that can be accurately represented as discrete sinusoids, although eigenvalue-based superresolution algorithms can outperform FFTs (e.g. MUSIC [3]). These algorithms are an essential part of the sound hunter quiver, and the reader should be familiar with them. Well-established algorithms and standards in the geophysical infrasound and seismic communities are described in [15]. However, these geophysical algorithms usually use arbitrary spectral computation parameters that are generally not transportable to other applications of infrasound, such as historical studies, noise and vibration control, and other research in low-frequency acoustics which adhere to ANSI and ISO standards for noise characterizations.
A limitation of Fourier synthesis is that the minimum window duration TW for array processing is fixed (Figure 1) and set by the lowest frequency (fci, in Hz), or the longest period (Tci = 1/fci) of interest,
 , (1)
, (1)
where NP is the number of periods in the window, L (km) is the array aperture or maximum element distance under consideration, and c (km/s) is the slowest speed of propagation of the wave type of interest, so that TL = L/c is the maximum time a signal may take to arrive at all the sensors. M is a scaling coefficient that compensates for window edge effects, filter ringing, and signal duration. M has a recommended range of 2 - 4, with a minimum of M = 2 when using a tapering window. If the microphones are collocated, or very close relative to a wavelength, then L = 0 and this contribution vanishes.
Fourier analysis is well suited for narrowband signals and linearly-spaced tones, when a high spectral resolution is desirable. However, the FFT fixed window duration does not generally provide a sufficiently fine temporal resolution. When analyzing a time-varying sound field over four decades in frequency, this type of windowing often leads to signal undersampling in the low frequency bands and oversampling at high frequencies (Figure 1). For commonly encountered non-stationary infrasonic signals, this often leads to unreliable statistics at both ends of the bandpass as well as unacceptable levels of ambiguity in arrival times and phase discrimination. For broadband non-stationary signals it is useful to consider alternative processing techniques that improve the temporal resolution in the characterization of signal and noise variability.
Fractional octave bands (Section 5) are traditionally used in environmental acoustics, sound and vibration [16]. Fractional octave schemas divide a bandpass of interest into overlapping, narrow bandpassed filter banks. For a narrowly bandpassed signal with a center frequency fc (with period Tc = 1/fc), a scaleable time window length for that passband may be defined as:
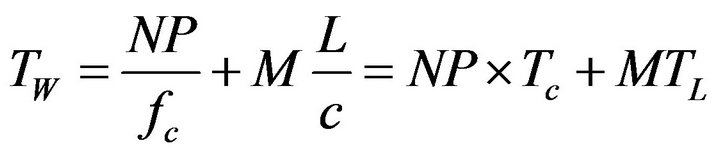 (2)
(2)
where NP represents the number of periods per band. In the absence of any preexisting knowledge about the target signature NP could have a range of 5 - 15, with NP = 10 (ten center periods per time window) a reasonable compromise. TL represents the minimum window length needed for the signal to traverse across the array at a speed c, and often sets the finest time resolution at high frequencies.
Using c = lc∙fc, this expression can be nondimensionalized as
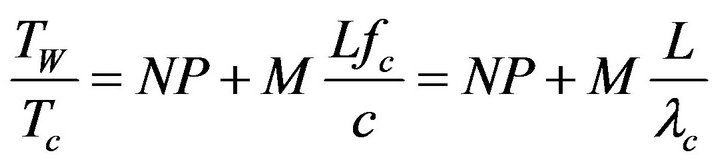 (3)
(3)
The second term in Equation (3) shows explicitly the effects of spatial aliasing and oversampling. From Section 2, this second term will be increasingly important in the spatially aliased wavenumber region where l < L.
As an example, for an array aperture of 2 km, a sound velocity of 0.34 km/s, NP = 10, and M = 4, Equation (2) can be simplified to:
 . (4)
. (4)
Note that as fc increases, TW approaches a constant value of 24 s. In effect, there is a cutoff frequency for which the 1/f scaling given by Equation (2) is not useful. This cutoff frequency is defined by
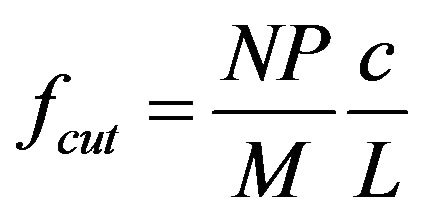 (5)
(5)
Let fci and fcf be the lowest and highest center frequencies in a filter bank. If fci > fcut, there is not much point in using 1/f scaling as it only makes the windows longer and degrades temporal resolution. In this case it is useful to set NP = 0 and use a constant window duration given by
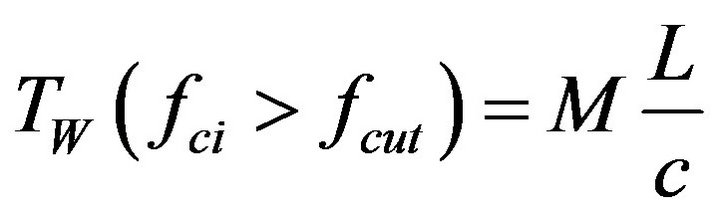 (6)
(6)
If fcf < fcut, it is counterproductive to use the constant array correction TL as this also degrades temporal resolution. In this case it is practical to set TL = 0 and use a window duration given by
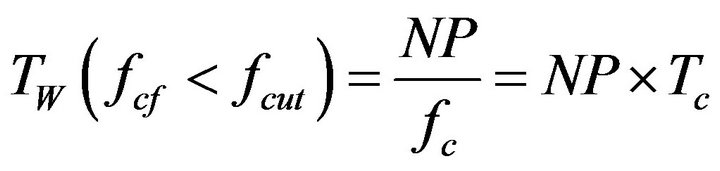 (7)
(7)
This corresponds to perfect 1/f scaling, and is the default solution to the case of L = 0 for processing single, adjacent sensors or networked sensors far from each other. For rapidly changing source processes, such as moving sources, TW should we minimized and could theoretically be lowered to the Gabor limit (Section 5).
These expressions provide a self-consistent method to autoscale a time window TW to the lowest frequency of interest fci when using standard FFTs with fixed window lengths, or to a center frequency fc when using filter banks. For the purposes of comparison, it is useful to select fci so that it matches the lowest third octave center frequency in a bandpass of interest.
Some array processing algorithms, such as Progressive Multiple Channel Correlation (PMCC), version 4 [17, 18], have already incorporated time window algorithms compatible with Equations (1)-(7) (Appendix A). Although the number of periods is here assumed to be an integer, this is not a requirement. For 1/f scaling, constant values for NP and M can be recovered from the relationships in Appendix A, where for fci < fcut
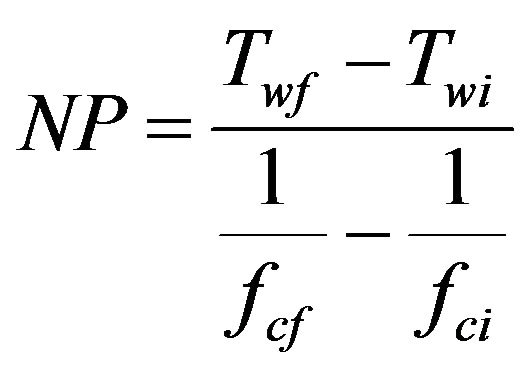 , (8)
, (8)
and for fcut < fcf,
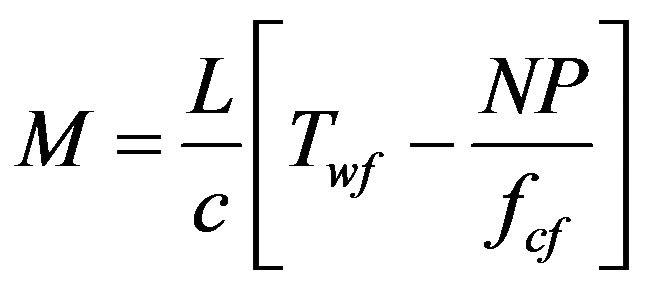 , (9)
, (9)
where Twi, fci are first and Twf, fcf are the last window durations and center frequency bands of interest. The aforementioned relationships can help an analyst reduce the number of free parameters and facilitate comparisons when designing detection configurations for a particular signal type and array geometry. More sophisticated expression with NP as a function of frequency could be developed, but are beyond the scope of this paper.
5. Scaling Frequency: Logarithmic Filter Banks
As mentioned in Section 3, to reproducibly track signal features over time and frequency along a propagation path it is useful to design a standardized set of frequency bins. In the case of classic Fourier synthesis the frequency bin size is fixed and is set by the fixed time duration, Df = 1/Twi (Equation (1)). However, in the case of filter banks the bandwidth increases with the center frequency, and it is possible to either have a constant time window or scale the time window so that it shrinks with increasing center frequency (Figure 1).
To standardize bandwidth scaling, this work extends fractional-octave band schemas [19,20] down to 0.001 Hz (1000 s periods), which includes some of the deepest acoustic-gravity and interface waves captured by the global IMS infrasound network [21]. However, some of these relationships could be applicable to the analysis of other propagating perturbations, such as barometric pressure [22] and surface wave height and wind speeds [23], whose records may extend over periods of months, years, or decades.
Filter banks in linear frequency spaces are used extensively in analogue and digital signal processing. Audio equalizers are examples of applied filter banks, with value placed on the ability to reconstruct the original sound. Filter banks in audio applications usually apply the discrete Fourier or continuous wavelet transforms, which are optimized with window lengths of 2n points. Although some software packages can create fractional octave bands in the audio range with ease, the algorithms in this section permit the ready construction of constant-quality-factor fractional octave filter banks with an arbitrary level of overlap down to the deep infrasound range.
Infrasonic 1/3 octave band central frequencies are specified in [20], which builds on the accepted 1/3 octave filter specifications given in [19, 24]. One advantage of the 1/3 octave filter is that 210/3 = 10.0794 ~ 10, so with some minor adjustments in the intervals it is possible to repeat the same schema every decade. Table 1 defines the preferred (nominal) central 1/3 octave band frequency (fc), lower half-power frequency (f1), and upper half-power frequency (f2). When the lower and upper half-power levels intersect, total power is recoverable by considering adjacent bands, with a possible overestimation of energy if the filter does not roll off sufficiently fast.
The band number, also referred to as the frequency level, is used to compute the exact band frequencies. In a strictly-defined 1/3-octave band, f2 = 21/3f1 and fc = 2n/3, where n is the band number and n = 0 yields the preferred reference frequency of 1 Hz [19]. The problem with using a binary base is that deviations from the computed and nominal frequencies increase as one moves away from the reference frequency. Instead, the preferred decimal base interval between exact frequencies is recommended, where 100.3 = 1.995 ~ 2. By setting:
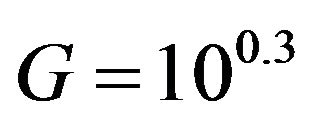 (10)
(10)
and defining the center frequency of an Nth octave band in the infrasound range as
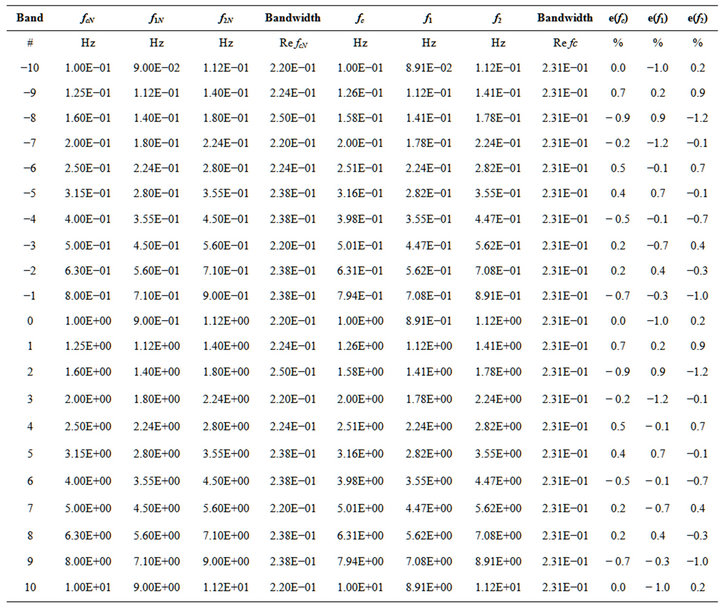
Table 1. Preferred frequencies (fcN, f1N, f2N) for nominal 1/3 octave bands and computed 1/3 octave bands (fc, f1, f2) extended to the infrasound range using G = 100.3. The scaled bandwidth bN1 and the percent error (e) between nominal and exact frequencies are shown in the last three columns. Note exact recurrence with every decade of frequency, so that this schema can be extended as deep in frequency as desired.
 (11)
(11)
where n = [‒30, 13] for N = 3 and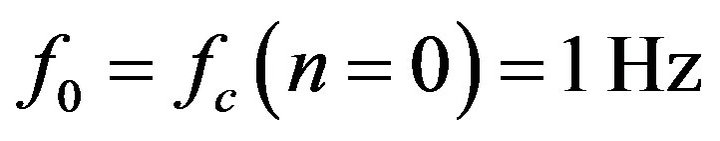 , yields a frequency range of 0.001 - 20 Hz. Note that n will rescale with N so that it matches the number of bands per octave, but it is always centered around f0 at n = 0.
, yields a frequency range of 0.001 - 20 Hz. Note that n will rescale with N so that it matches the number of bands per octave, but it is always centered around f0 at n = 0.
Defining
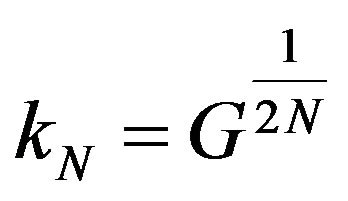 , (12)
, (12)
the half-power (bandedge) frequencies are
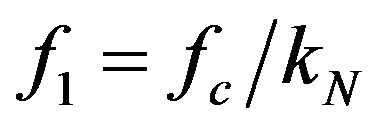 (13a)
(13a)
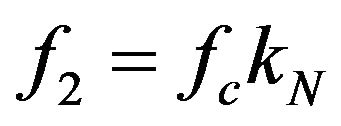 (13b)
(13b)
(Appendix 3). The central frequency fc of the proportional frequency band is the geometric mean of the lower (f1) and upper (f2) bandedge frequencies of the partitioning,
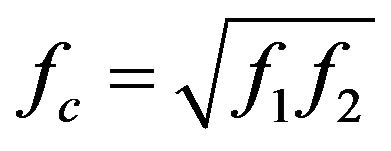 (14)
(14)
with
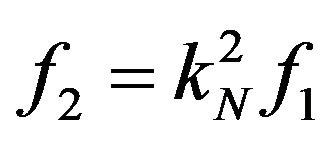 (15)
(15)
Yielding a constant-bandwidth filter set with scaled bandwidth
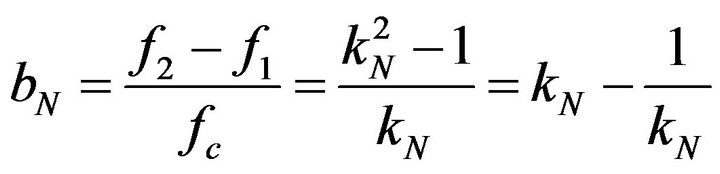 . (16)
. (16)
These stable, scalable properties make Nth octave bands useful building blocks. Unless otherwise stated, throughout the rest of this paper, fc, f1, f2 refer to the center frequency and upper and lower half-power bandedge frequencies for Nth octave bands. When referring to a specific band number n, the notation fcn or fc(n) is used.
Table 1 shows the computed 1/3 octave bands in the infrasound range, as well as the errors relative to the nominal bands. Errors are at most on the order of 1% from nominal, and both the computed frequencies as well as the errors recur every decade, as expected. This fractal schema can be propagated as deep into the infrasound range as desired with predictable results. Due to the small errors, it is preferable to use the exact rather than the nominal frequencies in computations. However, as per [24,30], the nominal rounded values should be used in labeling for simplicity.
For 1/3 octave bands, kN = 1.12 and bN = 0.0231, as shown in Table 1. Note these formulations can be used for any Nth octave band, but are particularly well suited for intervals of thirds, where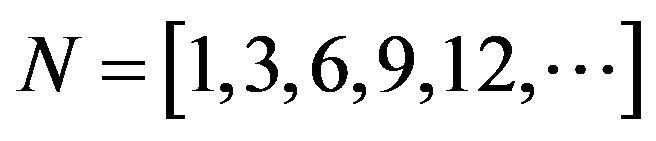 . Table 2 shows the fractal nature of logarithmically spaced fractional octave bands and how this schema imbeds a recurring binary system within a decimal system. When N is an odd multiple of three we can contract from higher to lower orders quite exactly, whereas when N is even we have to split bands to recover an octave.
. Table 2 shows the fractal nature of logarithmically spaced fractional octave bands and how this schema imbeds a recurring binary system within a decimal system. When N is an odd multiple of three we can contract from higher to lower orders quite exactly, whereas when N is even we have to split bands to recover an octave.
When designing fractional octave band filters in logarithmic frequency spaces it is desirable to use evenlyspaced center frequencies as they yield the most stable and self-similar filter amplitude and phase responses. This can be readily accomplished by using Equations (10)-(16). However, an alternative method, used in PMCC4 and consistent with the aforementioned intervals, defines the lowest and highest frequency of interest, as well as the number of bands NF (Appendix B).
Figure 3 shows evenly log-spaced 1/3 octave bands with −3dB (half-power) bandedgeoverlap using 2nd order Chebyshev bandpass filters, which may not yield the highest precision on energy estimates but are stable over the 0.01 - 5 Hz IMS monitoring band (Appendix C). An assessment of detector performance using various filter banks with varying bandedge overlap is beyond the scope of this paper, although preliminary tests demonstrated that the accuracy of the infrasonic energy estimates will depend on these filter bank properties.
5.1. Some Practical Considerations
From the practical standpoint of numerical evaluation, the number of points (Nw) in a time window could be estimated from
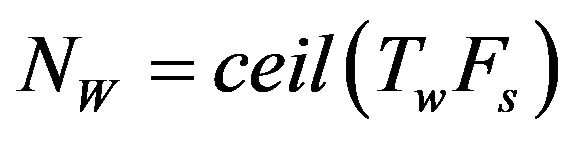 , (17)
, (17)
where Fs is the sampling frequency and ceil(x) denotes the operation of rounding up x to nearest integer. If there is no requirement to minimize the number of points in a window, or use powers of two, Equation (2) can be readily implemented as is.
However, there are many instances where it is desirable to minimize the window duration so as to improve the temporal resolution of rapidly varying signals. The theoretical minimum window duration in relation to the spectral resolution Df can be estimated from the Gabor limit [25], also known as the time-frequency uncertainty principle
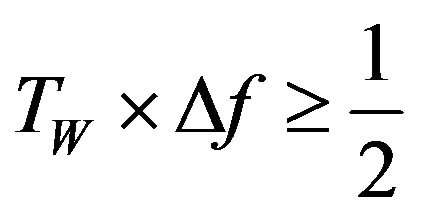 . (18)
. (18)
This condition is always satisfied by appropriately scaled FFT windows, where Df = 1/Tw. Although there are various expressions for this version of the uncertainty principle, the original Gabor [25] exposition is clear, simple, and beautiful.
For fractional octave bands where Dfc = f2 − f1, this yields
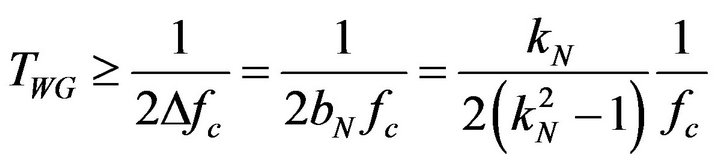 . (19)
. (19)
By using Equations (2)-(18) for the case fci < fc < fcf
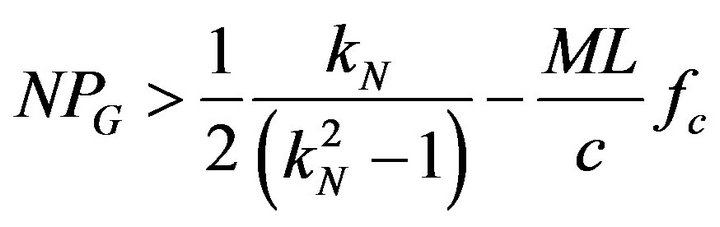 . (20)
. (20)
Although at first glance the minimum number of periods appears to diminish with increasing center frequency and array aperture, this is an artifact of the way Equation (2) compensates for the array aperture contribution, which is most pronounced with spatially aliased frequen-
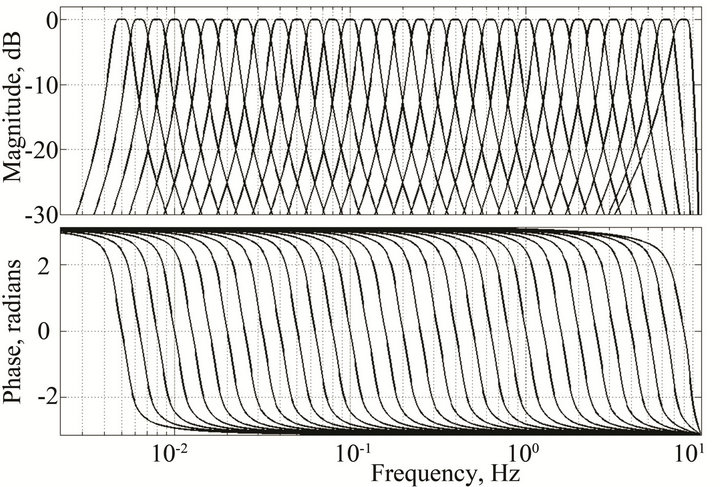
Figure 3. Third-octave, 2nd order Chebyshev filter sets from 5 mHz to 8 Hz (33 bands) with 1/2 power bandedge overlap. This filter set meets and exceeds the IMS bandpass of 0.02 - 5 Hz. Note that for the IMS sample rate of 20 Hz the response of the highest bands steepens as the Nyquist frequency is approached. This filter bank also becomes numerically unstable below 4 mHz without decimation.
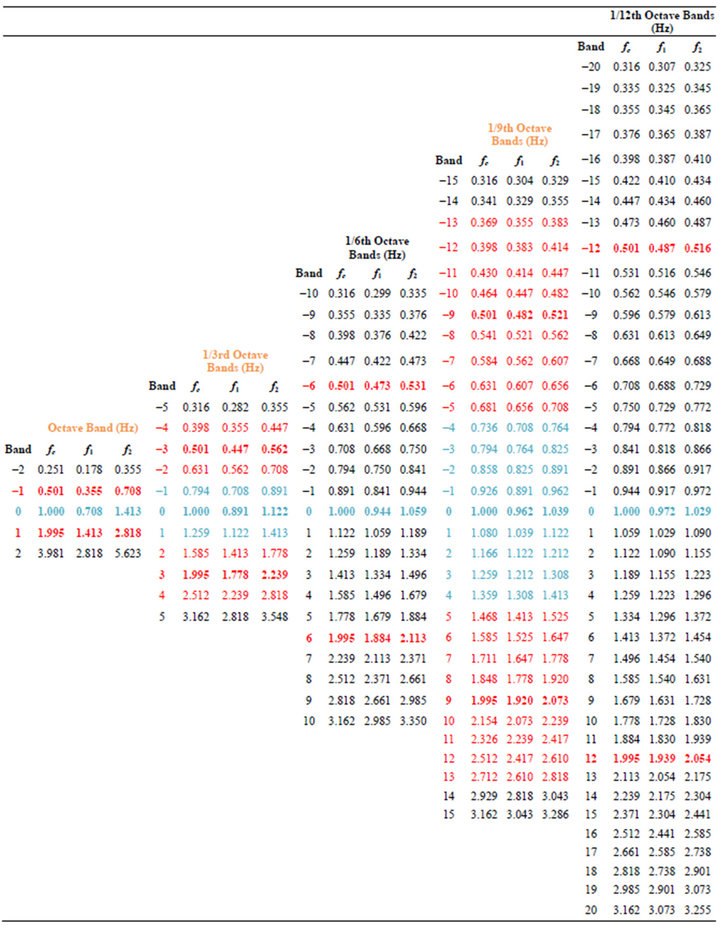
Table 2. Octave and fractional octave bands between 0.316 and 3.16 Hz. Pattern repeats every decade with G = 1.9953, reference frequency of 1 Hz.
cies. Implementation of Equations (6)-(9) yields reasonable results.
For fci < fcut and at the low frequencies where 1/f scaling is most useful, the minimum number of periods in a given Nth octave band valid for all array apertures can be estimated from
 (21)
(21)
Figure 4 shows the minimum number of periods NP0 that should be used to satisfy the Gabor limit as a function of the selected Nth octave band. As expected, the narrower the band (higher N), the longer the time window should be to meet the uncertainty principle. Although NP has been treated as an integer to represent the average number of oscillations per window, it may also be defined as a continuous function of central frequency to meet a specified performance criterion.
The first wavelet was described by [25] by multiplying a sinusoid by a Gaussian envelope. This continuous wavelet, also known as the Morlet wavelet, is designed to meet the Gabor limit and provides a set of basis functions with the shortest theoretical time window, or highest temporal resolution per band. Although wavelet representations are beyond the scope of this paper, the concepts presented here would permit self-consistent comparisons between FFT, fractional octave, and wavelet representations of diverse sound fields [26].
This suggests that the Gabor window length can be used as a reference standard in place of the number of periods, NP. If the Gabor window is defined as
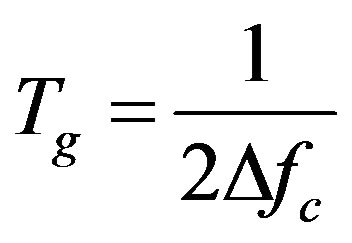 , (22)
, (22)

Figure 4. Minimum number of periods (NP) required to meet the Gabor limit (Equation (21)) for a given Nth octave band specification. Note this theoretical value may be less than unity for octave bands, but is ~2 for 1/3 octave bands. As N increases, Df gets narrower, the filters tend to ring longer, and more periods NP are needed to contain a signal.
the time windows may be scaled in relation to the Gabor window such that
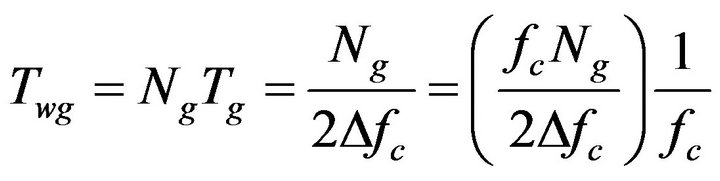 . (23)
. (23)
This expression applies to both linearly spaced and logarithmically spaced frequency bands. However, for constant-bandwidth Nth octave bands, this has the added advantage of reducing to,
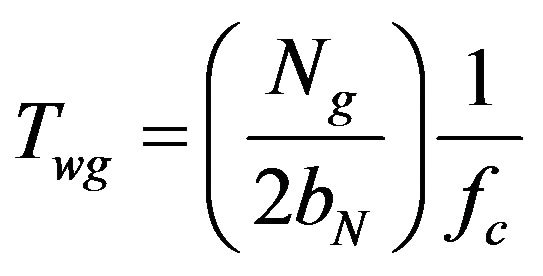 , (24)
, (24)
where bN is constant. For the case fc < fcut, we can use this expression to minimize the window duration at the lowest frequency.
Further constraints can be placed if we wish to compare our results to FFT and continuous wavelet representations, where it may be useful to make the number of points in the starting and ending windows an integer power of two.
As shown in Appendix A, the PMCC4 algorithm uses a frequency counter  instead of the band number n, with a simple linear conversion between them. Let Tw(1) and fci be the time windows and center frequencies for the first (lowest) frequency band, and Tw(NF) and fcf the time windows and center frequencies for the last frequency band. Only when fci < fc < fcf can window lengths be specified for both the first and last windows. The number of points in the longest and shortest window would then be
instead of the band number n, with a simple linear conversion between them. Let Tw(1) and fci be the time windows and center frequencies for the first (lowest) frequency band, and Tw(NF) and fcf the time windows and center frequencies for the last frequency band. Only when fci < fc < fcf can window lengths be specified for both the first and last windows. The number of points in the longest and shortest window would then be
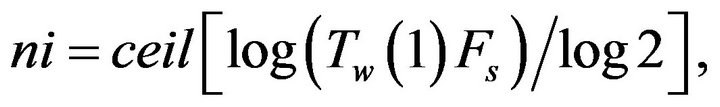 (25)
(25)
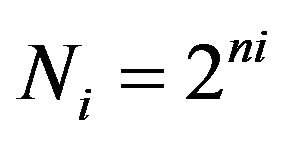
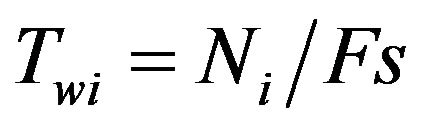
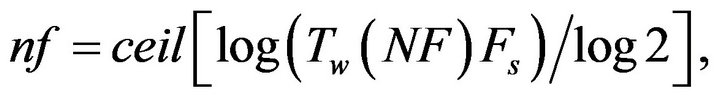 (26)
(26)

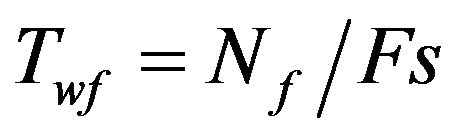
which will yield a non-integer number of periods NP or NPg of
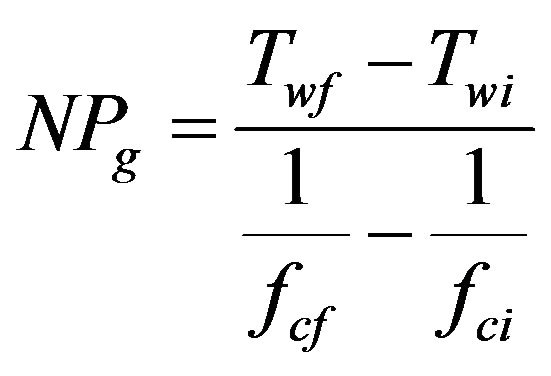 (27)
(27)
as given by Equation (8). A revised version of Equation (2) can be defined with Gabor scaling, where an estimate of Mg is obtained from Equation (9) when fcut < fcf.
As in Section 4, 1/f Gabor window scaling is only useful in the case of fci < fcut (Equation (7)), otherwise a constant window duration should be used (Equation (8)).
Perfect 1/f scaling occurs when fcf < fcut (Equation (7)), when only the shortest or the longest window length can be specified, but not both. In that case it is recommended that Tw(1) be specified for comparison with fixed time window algorithms. Note that once array processing is performed and a beam is formed, TL is no longer needed and perfect 1/f Gabor scaling (Equation (24)) can be used to minimize the window length when a finer temporal resolution is desired.
5.2. Soundscape Standards
Ambient sounds are described in ANSI standards [27,28] in terms of their amplitude, temporal, spectral, and directional characteristics. In the time domain, a signal may be described as continuous steady, fluctuating, and impulsive, or intermittent steady, fluctuating, and impulsive. In the frequency domain, a sound of interest may be categorized as broadband, narrowband, tones, or a combination. If a signal is high in harmonics, higher Nth order filters may be needed to capture the finer spectral detail.
Although these descriptors provide a valuable starting point for general signal classification, they are insufficient to describe some signals, such as chirps. In addition, some of the ANSI specifications for impulsive sound [27, 29] invoke the use of A-weighting [30] to account for the response of the human ear down to 20 Hz, which is not very useful in the infrasound range. For most infrasonic environmental impact and industrial noise applications down to 0.25 Hz, the G-weighting [20] is more pertinent [31]. It is possible to correct back to unweighted SPLs by removing the Aor G-weights specified in these standards. Only unweighted SPL’s are presented in this paper.
Additional ambient sound descriptors may be derived from the ecologically-minded soundscape community. A soundscape is defined as “an environment of sound (sonic environment) with emphasis on the way it is perceived and understood by the individual, or by a society” [32]. Much of the perceived impact of wind turbine infrasound falls under the soundscape rubric and [33], as may also prove to be the case for next-generation active source systems. In lieu of a cohesive system for signal classification, most acoustics communities develop fieldspecific taxonomies [34,35].
6. Scaling Amplitude: Power and Energy Estimates
Scaling laws for long-range propagation of infrasound are as abundant as they are fickle. One problem with these scaling laws is that they often refer to an equivalent TNT yield, therefore presupposing a detonating highexplosive source that poorly represents most transient natural sources (including volcanoes and meteors), and completely misrepresents most soundscapes. Many of these scaling laws seek to predict the peak pressure, period, or duration of a signal as a function of yield, range and sometimes stratospheric wind (at ~50 km). Since there are no conservation laws for pressure, period, or duration (Section 3), this work concentrates on obtaining the spectral distribution of energy transfer along a propagation path. The sound pressure level [27,36-38] provides a common, traceable framework for estimating infrasonic signal energy (Section 6).
To facilitate inter-disciplinary collaboration, infrasonic results could at a minimum be reported in sound pressure levels (SPL, in dB) referenced to 20 mPa, in one-third octave bands. When the source distance is specified and atmospheric propagation effects are known, they could be normalized to a distance of one meter. A similar minimum requirement, with procedures, was adopted by the ASA for the measurement of underwater sound from ships [39].
When estimating signal energy it is possible to discriminate from ambient clutter [3] and incoherent noise with array processing. It is also valuable to evaluate the power levels for the combined incoherent and coherent pressure contributions to produce an estimate of data quality and array performance.
6.1. Sound Pressure Levels (SPL)
One of the most fundamental acoustic measurements is pressure amplitude [28,33,36]. Since acoustic signals can span over 12 orders of magnitude in sound intensity, it is useful to adopt the SPL logarithmic scale [27] for rootmean-square (rms) pressure prms:
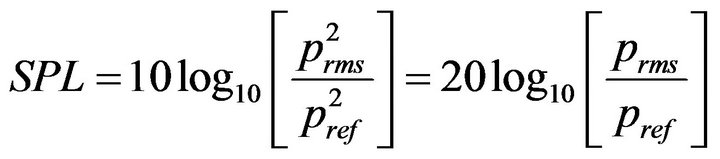 (28)
(28)
where
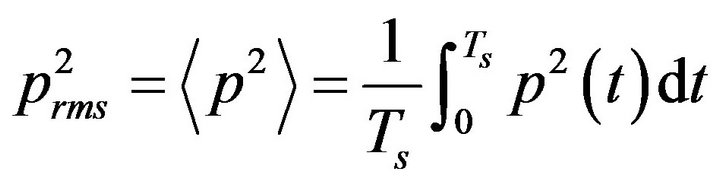 , (29)
, (29)
and pref = 20 mPa is the reference rms pressure, p is the acoustic pressure time series over a specified frequency band, and Ts is the signal duration or the chosen time interval for integration. Although this paper concentrates on the acoustic pressure relative to ANSI and ISO standards, the process of signal energy estimation using the windowed rms of its amplitude can be generalized to other digital time series data with or without known calibrations. If a sensor calibration is not known, the units of signal amplitude could be counts or volts and the signal can be scaled to either the known dynamic range of the digitizer or to a reference sensor.
Root-mean-square pressure (prms) estimates are robust when the acoustic signal is stationary, so that its statistical properties do not change substantially over the period of integration. For a continuous signal of constant period, prms can be approximated by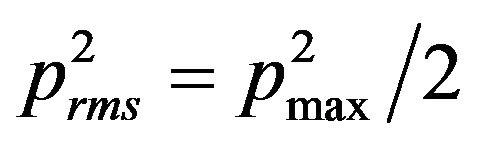 , where pmax is the peak pressure in Pascals. However, for impulsive, transient signals such as explosions, the integration interval should match the signal duration to provide a sound exposure level
, where pmax is the peak pressure in Pascals. However, for impulsive, transient signals such as explosions, the integration interval should match the signal duration to provide a sound exposure level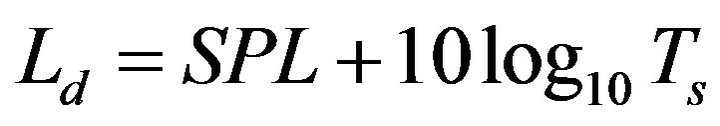 . The reference level of sound exposure in air is (20 mPa)2 s [29]. The SPL or Ld are not accurate without a specification of the frequency band used to compute the scaled time window in Equation (2) and a correction for the data acquisition response in that band [27].
. The reference level of sound exposure in air is (20 mPa)2 s [29]. The SPL or Ld are not accurate without a specification of the frequency band used to compute the scaled time window in Equation (2) and a correction for the data acquisition response in that band [27].
Sound intensity I, in Watts m−2, is a measure of the average rate of acoustic energy flow through an area normal to the propagation direction, and is proportional to the square of the pressure far from the source. The intensity can be estimated from
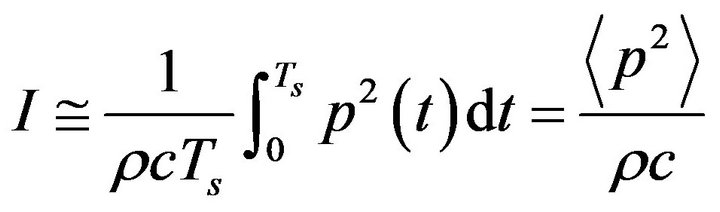 (30)
(30)
where the sound speed c and the equilibrium density r of Earth’s atmosphere at 20˚C and sea level pressures are 343 m/s and 1.2 kg/m3, respectively. Since there is only a proportionality factor (rc ~ 400 kg/m2×s) between intensity and the square of pressure, SPL estimates can be readily converted to intensity by using a reference intensity level Iref = 10‒12 W×m‒2 in air (Equation (30)). Intensity estimates are useful for comparing the acoustic response of different environments. The total exposure energy E in J×m‒2 in a time window Ts would be estimated from E = I×Ts. The exposure is a measure of the total instantaneous energy, whereas the intensity provides a useful measure of the average power. Thus transients are generally best characterized by the exposure in Joules/m2, and more continuous sounds by the average intensity in Watts/m2.
Practical algorithms for computing the rms and power spectral density of digital signals are provided in [15]. In practice, the signal duration Ts is not known is and the window duration Tw is generally used in its place. By substituting the integral in Equation (29) by a sum over all the discrete pressure data points q in a window of total length Q, the rms pressure can be estimated from
 . (31)
. (31)
For a properly conditioned signal (with the mean removed), this can be readily recognized as the variance of the acoustic pressure over the time window. The next sections discuss how the SPL, intensity, and exposure per frequency band can be readily evaluated in the frequency and time domains.
6.2. SPLs from the Power Spectral Density
Parseval’s Theorem provides a relationship for the variance and the power spectral density (PSD) of a digital pressure signal [15,40], with units of Pa2/Hz. The PSD can be readily computed by the FFT over a finite time window and provides an estimate of the mean squared acoustic pressure per frequency band in the time window.
The decibel unit for PSD is dB relative to (20 μPa)2/Hz, which is referred to as the spectral level. A spectrogram is a time-stepping PSD, and is useful for interpreting time-varying signals. To convert spectral levels to sound pressure levels, a particular frequency band has to be defined. Suppose the unilateral PSD of a signal has already been calculated [15]. The SPL in a frequency band Df12 can be estimated from the PSD P(f) from:
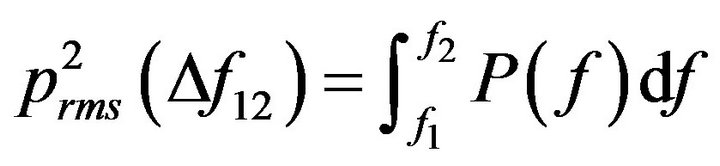 (32)
(32)
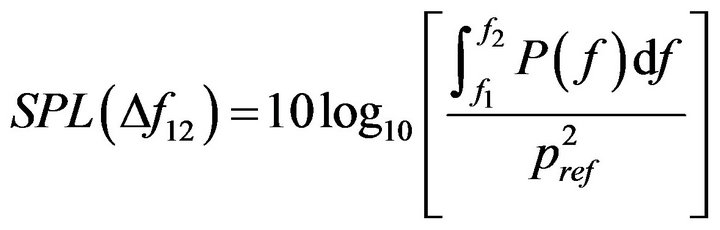 . (33)
. (33)
If P(f) is very slowly varying or nearly constant over a fractional octave band, we can estimate the sound pressure level on band n from
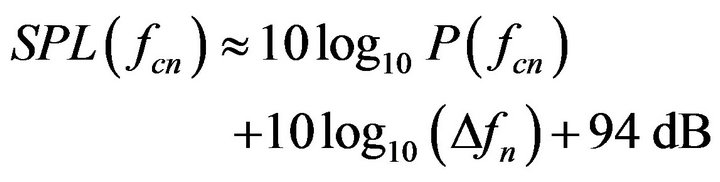 , (34)
, (34)
where fcn is the center frequency, Dfn is the bandwidth of the nth frequency band (Table 1), and pref = 20 mPa (−94 dB) is the reference rms pressure. If P(f) is not slowly varying, numerical integration over the bandpass is preferable.
From Equations (28)-(30)
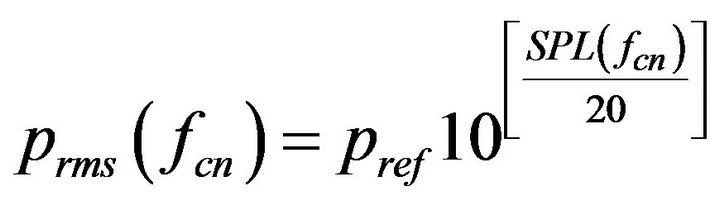 (35)
(35)
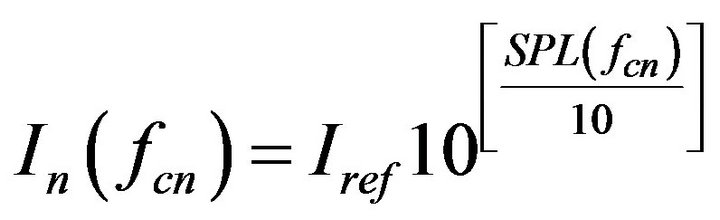 . (36)
. (36)
The total average intensity over the frequency band can be expressed as a sum of the intensity in each discrete frequency component (see notation in Appendix B) over the total band :
:
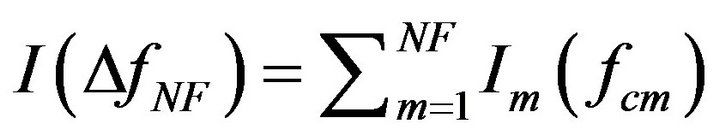 . (37)
. (37)
It is assumed that each frequency bin is sufficiently well separated that there is minimal spectral leakage between adjacent bands. Numerical integration over the clearly defined bandedges in Equation (33) would ensure this condition is satisfied, as would well-defined filter banks with bandedge overlap at the −3 dB point (Appendix C).
Equation (37) is equivalent to
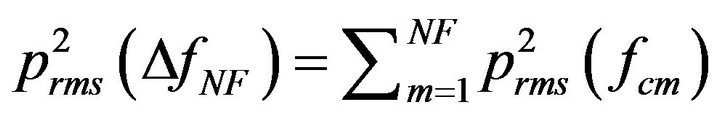 . (38)
. (38)
This is an alternate expression for the conservation of energy, and is consistent with the formulations in [38]. The total SPL over a band can be estimated by applying Equations (28)-(38).
As an example, the global ambient noise models in the IMS infrasound detection band [41-43] shown in Figure 5 are converted from spectral levels to 1/3-octave bands (Figure 6). Since the Bowman curves cover the bandwidth of 0.308 - 7.2419 Hz, only 1/3-octave bands n = −14 to n = 8 (0.04 - 7.1 Hz) overlap. If we estimate the total area under the Bowman curves using mid-point integration (Equation 34) and summing over all bands, the intensity estimates are higher than those derived from integration only over the predefined 1/3-octave bands. The SPLs estimated from trapezoidal integration in 1/3 - octave bands are shown on Figure 6, and could be used as alternate reference standards for evaluating detection probabilities and data quality. Note the lower frequencies, although flattened relative to the PSD curves, still have the largest contribution to the total energy budget, suggesting that the region in the PSD with the highest amplitude and rate of change should be integrated with care.
6.3. SPLs from Time-Domain Signatures
The Sound Level Meter [19,30] is one of the key acoustician’s tool for the characterization of environmental noise. The design and use of these devices are regulated by clear standards which routinely extend down to 6.3
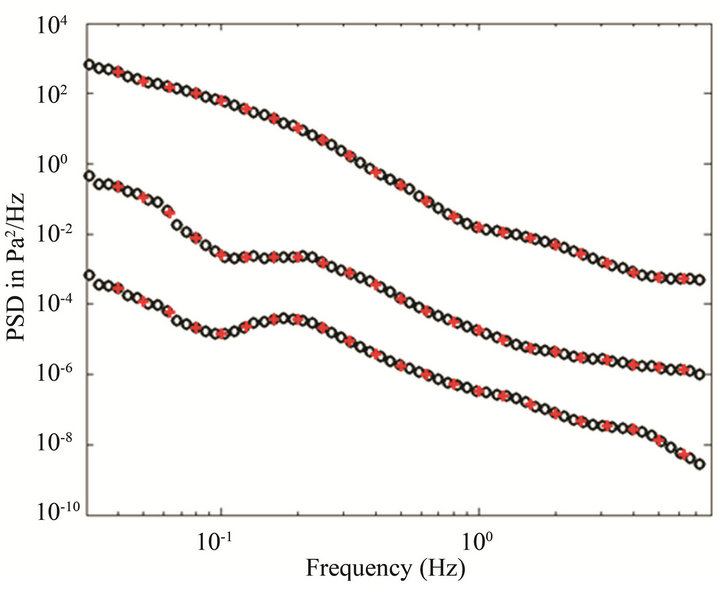
Figure 5. PSD in 0.308 - 7.2419 Hz band derived from the global IMS infrasound network. The three curves correspond to the high, median, and low noise models. The black circles show the original data in ~1/8-octave bands, and the red crosses are the interpolated values at the central 1/3- octave frequencies. Note that the first 1/3-octave band within the interpolation range has a center frequency of 0.04 Hz (band-14).
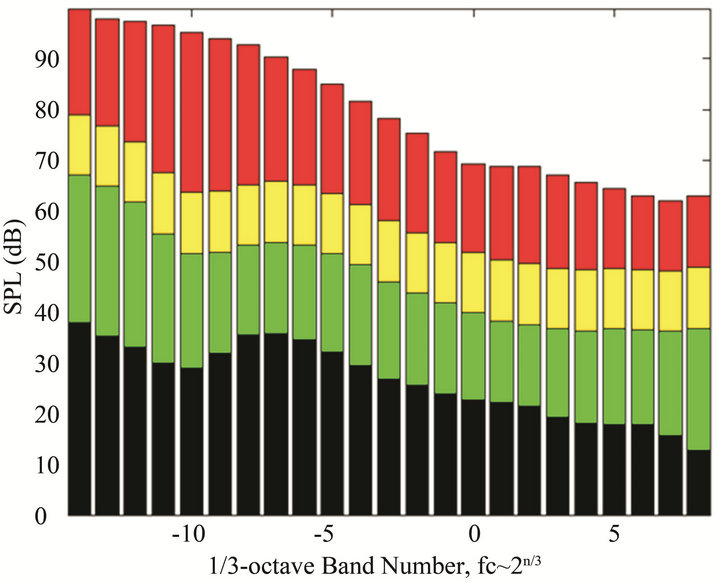
Figure 6. Sound Pressure Level (or Intensity Level) per 1/3 - octave band for Figure 5 using trapezoidal integration per band. Black regions are below the low-noise levels, green are above low but below median, yellow indicates a range of 12 db (factor of 4 in amplitude), and red extends to the high noise regime. Signal detection probabilities in the green zone would be high, in the yellow, marginal, in the red, low.
Hz and lower [20,33].
The FFT and its derivative products assume a fixed window length, which could be derived using Equation (1). This presupposes that the statistical properties of the signal are stationary over the time window and across the processing band, an often reasonable assumption for stable, continuous, near-field processes. It is possible to reproduce the results of Fourier synthesis by applying the filter banks discussed in Section 5 over overlapping time windows of fixed duration (Figure 1, third panel from top). However, working in the time domain permits the integration of frequency-scaled window durations which will increase the spectral resolution at all frequencies above fci in Equation (1). This approach is desirable for broadband signals that may have multiple sources and/or arrivals, and its implementation is succinctly described in this section.
The Infrasonic Energy, Nth Octave (INFERNO) multiresolution algorithm is a conceptually simple energy estimator, and involves applying the filter banks defined in Equations (10)-(16) to a waveform of interest after proper preconditioning by detrending and applying a taper window to minimize DC offsets and ringing at the window edges. Care should also be taken around data gaps and other discontinuities, which will also produce spikes and ringing when filtered. The filtered waveforms are then divided into possibly overlapped windows using the scaled duration defined in Equation (2), and the variance is computed for each window. If further computations are intended, it may be desirable to detrend and taper each subwindow instead to improve stability. The resulting variance matrix will be non-rectangular. The NF frequency bins could be evenly spaced in logarithmic or linear frequency, but when using Equation (2) the NT(fcn) time windows will depend on the frequency bin and be unevenly spaced in linear time. For efficient matrix manipulation and display, the time scale can be homogenized by rebinning using the smallest time window as the reference time granularity. The end result is a rectangular intensity matrix I[ti, fcn] that provides an estimate of signal power as a function of time and log frequency.
Regardless of window overlapping, the time-averaged intensity for a given center frequency is
 (39)
(39)
with Equation (37) providing the total intensity over all frequency bands. These intensity estimates should be compatible to those derived from PSD integration. By comparing the ratio of the intensity per bin I[ti, fcn] to the intensity averaged over a specified number of time windows it is possible to define an instantaneous S/N per bin (Figure 2). Evaluating the ratio of the intensity in Equation 39 using a different number of windows NTS and NTL could yield results comparable to the fixed-window short-time to long-time average methods (STA/LTA) used in seismology, where STA/LTA is 1 s/60 s for IMS seismic monitoring. Alternatively, it would be possible to define NPS and NPL in Equation (2), where NPL > NPS, and compute the ratio of the instantaneous intensity using NPS relative to a moving averaged intensity (Equation (39)) computed using NPL.
Estimating the total exposure in the case of overlapped frequency-scaled time windows requires a bit more care. When the intensity matrix is rectangular, the number of frequency banks is unchanged but the time grid remapped to the finest time step TW(NF). Since the intensity is already an average of the energy over the window, it can be subdivided as much as desired to yield the same average intensity per unit time. From Section 6.1, the exposure per bin in the rectangular matrix can be is defined as
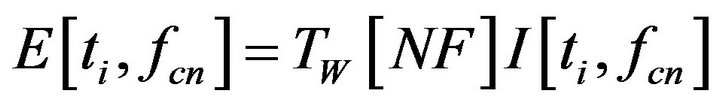 (40)
(40)
Let NT be the total number of overlapped, adjacent time windows in a rectangular intensity matrix. When wp is the normalized percent window overlap between [0, 1), the total exposure per frequency bin over a time period of interest can be estimated from:
 , (41a)
, (41a)
or
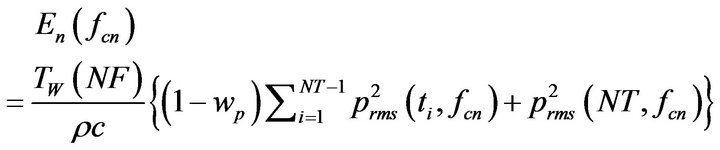 , (41b)
, (41b)
which yields an estimate of the total energy in J/m−2 per frequency bin. These two equations only differ in which of the time pixels is added in its totality, and Equation (41a) may be particularly useful for flagging impulsive onsets. However, since an infrasonic signal may have an impulsive onset but almost always has a slow decay that fades into the background, the last time window contribution in Equation (41b) is often negligible and the total exposure per band may be estimated by
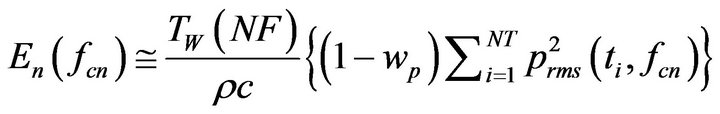 (42)
(42)
Note that this energy estimate is not averaged over all windows as in Equation (39), but is instead a cumulative sum of weighted rms pressures. As discussed in the previous section, it would be possible to set up a time-stepping, energy-based triggering algorithm comparable to STA/LTA using the exposure instead of the intensity.
In the event of no overlapping windows, wp = 0 and
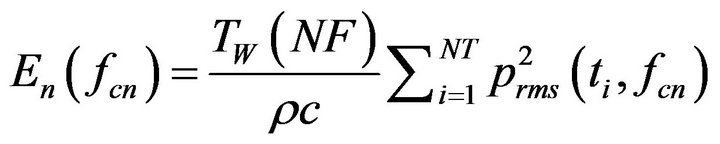 . (43)
. (43)
The sum of the exposure over all frequency bins provides an estimate of the total energy observed over a band of interest.
Implementation of this algorithm can offer significant improvements in the ability to recognize distinct arrivals in broadband signals and improve estimates for their energy, onset time (Figure 2), and frequency-dependent trace velocity and azimuth statistics. This procedure allows high-resolution broadband spectral analysis in standardized logarithmic-frequency spaces with time window autoscaling. In many ways this approach is reminiscent of wavelet transforms (e.g. [26]), without abandoning sinusoids as basis functions or the familiar concepts of energy and frequency. The results are compatible with the results of FFT analyses in the case of fixed window lengths. In addition, since this formulation is compatible with the PMCC4 time-frequency grids, careful implementation permits an integration with array processing results to estimate coherent versus incoherent energy as well as the separation of contributions from competing sources. It is expected that standardized temporal and spectral parameters can facilitate comparative calibrations, source characterizations, and the benchmarking of array processing algorithms.
7. Praxis: Russian Meteor
A meteor was observed over Russia on 15 February 2013, and its infrasonic signature was captured worldwide [44].
A description of this event is beyond the scope of this work, as is a deconstruction of the meteor trajectory. This section concentrates on estimating the infrasonic energy in the 4.5 mHz to 9 Hz frequency band using different methods. We use array data from IMS infrasound array I31KZ, Kazakhstan, to estimate the total acoustic energy observed at the station.
Three different approaches are used. The reference energy is obtained from direct integration in the bandpass of interest over the known signal time, but does not deconvolve the sensor response because of uncertainties in the complex transfer function of wind filters. Although this is the most immediate and direct estimate, it will tend to overestimate the total energy as it incorporates both signal and noise. The array processing method utilizes only the coherent energy observed by the 8-element array beam. The S/N approach uses the array results to reduce source ambiguity, but relies on the S/N ratio per band as the signal cutoff criterion. The last two methods correct for the known amplitude response of the MB2000 pressure sensor.
7.1. Array Processing with 1/3 Octave Bands
As mentioned in Section 4, PMCC4 can incorporate fractional octave bands and time window scaling as described in Equation (2). For this study, the number of PMCC 1/3 octave bands is set to 33, with a maximum frequency of 8.9125 Hz and a minimum frequency of 0.0045 Hz. For an IMS-type array aperture of ~2 km, NP = 5, M = 4 yield a maximum window duration of 1021.2000 s and a minimum window duration of 24.2000 s (Equation (2)). The window overlap is 75% (0.75 in Equation (42)). With this parameter set, the longest center period Tci is 199.5262 s (~5 mHz). Although it is likely that there is coherent energy at longer periods, IMS arrays are not designed for array processing of acoustic signals in the mHz range (Section 2). Typical values for the threshold consistency (0.1), minimum number of sensors (3), qLambda (50) and family values (Threshold distance = 1, sigma rms = 100, ThreshFamMax = 300, sigma_f: 50%, ThreshFamMin: 5, Sigma_t = 200%, ThresholdDate: 200%) were used, but since the source was moving quite fast a high tolerance in azimuth (30˚) and speed (30%) variability was allowed.
Although PMCC4 uses filter bands with 0 dB bandedge overlap, the SPL estimates presented in Figures 7 and 8 use the filter banks shown in Figure 3 with a −3 dB bandedge overlap (Appendix C). In contrast to Figure 2, the MB2000 instrument response was removed for the energy estimates described in this section.
Figure 7 shows the beamformed waveform (first panel) and coherent energy in dB (second panel) computed by PMCC4 with the aforementioned processing parameters.
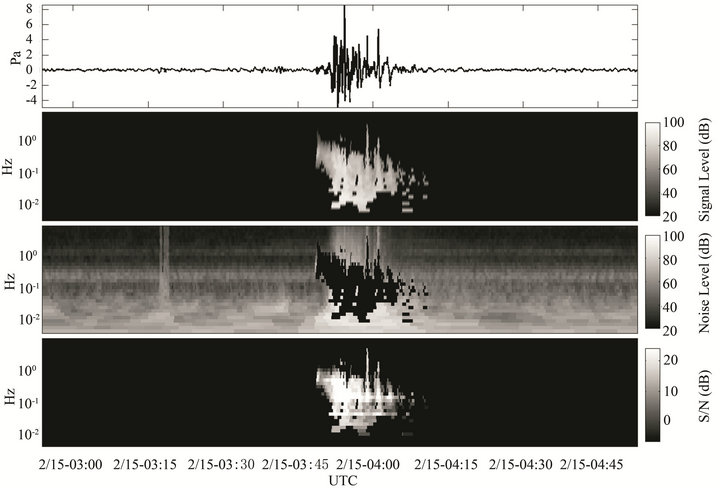
Figure 7. PMCC4 array processing results showing the waveform (first panel), coherent signal levels within specified speed, azimuth, and coherence masks (second panel), the remaining ambient field outside of the specified parameter set (third panel), and the signal to nose ratio estimated by using the ambient field over the record as the reference noise (bottom panel).The spike associated with a data drop just after 3:15 does not show up in the array processing.
Only coherent arrivals with a correlation greater than 0.8, arrival azimuths between 0 and 58 degrees, and a speed within the narrow range of 0.33 - 0.35 km/s are kept. These parameters are selected to keep only the most reliable and accurate coherent arrivals and to illustrate some of the possible issues that may arise from the exclusive use of array processing results to estimate infrasonic energy. The maximum energy beam within this parameter subset set is used. The third panel in Figure 7 shows the ambient field remaining after the removal of the signal, and is used to construct the average background noise specifications (Equation (39)). The fourth panel shows the S/N ratio in dB using this background noise as a reference.
Figure 8 shows a similar procedure, but using S/N rather than array processing as the primary criterion. The procedure is reminiscent of the short-time/long-time averaging (STA/LTA) routinely performed in seismic studies, where here a reference noise specification is constructed from a longer term average or a sample record obtained before the signal arrival.
7.2. Signal Detection Using Energy
In contrast to using the energy remaining after the removal of the coherent signal as the reference noise (Figure 7), a relatively quiet record segment is selected as the reference noise model. We apply the INFERNO algorithm using the same 1/3 octave bands and window lengths as in Section 7.1 to the same beam (Figure 8, first and second panels). As can be seen in the third panel of Figure 8, a more careful selection of the reference noise yields an S/N increase in excess of 24 dB for this exceptionally broadband, energetic record. This is not surprising, as Figure 7 shows that much of the energy previously considered as “noise” is coincident with the “signal”. If it is assumed that the majority of the energy arriving at the station at ~0400 UTC originated from the meteor, this procedure also demonstrates how much of the event energy may not be picked up by array processing. The infrasonic energy may not appear coherent to the array due to multipathing, phase mismatches at the elements, or wavefront distortions induced by topography, nonlinearity, or atmospheric scintillation.
7.3. Estimating the Observed Event Energy
The array processing and S/N results provide a fairly robust indication of the temporal distribution of the signal. Direct integration of the bandpassed, squared pressure (Section 6.1, Equation (30)) over the signal duration estimated in Section 7.2 yields an energy estimate of 4.4 J/m2, whereas integration of the whole record yields 4.7 J/m2. Thus the majority (~94%) of the energy in the ~2 h
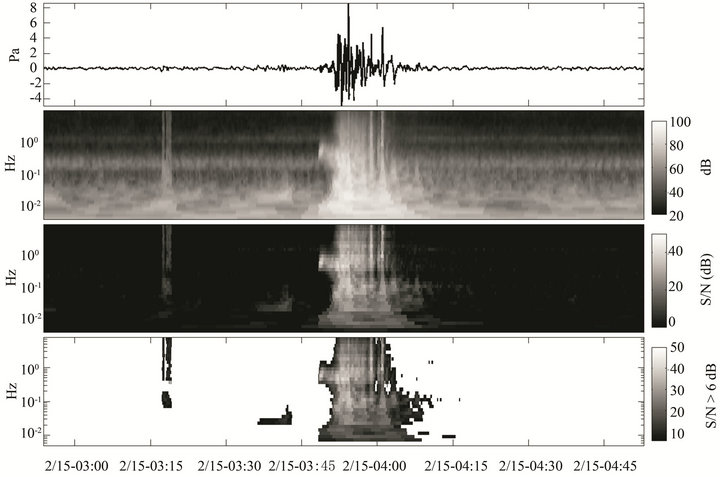
Figure 8. S/N threshold results showing the waveform (first panel), the instrument-corrected infrasonic intensity over the record (second panel), the S/N estimated by using a selected part of the record as the reference noise (third panel), and the extraction of the spectral components with S/N > 6 dB (bottom panel).The spike associated with the data drop just after 3:15 can be clearly seen.
record is from the signal of interest.
When using filter banks with 1/2 power (−3 dB) overlap at the bandedge frequency, as shown in Figure 3, the array processing method (Figure 7) yields a coherent signal energy estimate of 2.0 J/m2 and a total record energy of 4.3 J/m2, which corresponds to an underestimate of 45% (−3.4 dB) for the signal energy and a slight underestimate of 97% (−0.1 dB) for the total record energy. Thus by restricting energy estimates to those derived from only the most accurate array processing results with high correlation values, the total signal energy may be underestimated by at least a factor of two (3 dB).
The INFERNO S/N approach uses only contributions with an S/N > 6 dB (Figure 8, bottom panel) to derive a total signal energy estimate of 3.9 J/m2, which is 87% (−0.5 dB) of the integrated signal energy. By lowering the S/N threshold and using contributions with an S/N > −3 dB, the energy estimate increases to 4.2 J/m2 which is 95% (−0.2 dB) of the integrated signal energy.
If using filter banks with 0 dB bandedge overlap, the array processing method yields a coherent signal energy estimate of 8.1 J/m2 and a total record energy of 19.5 J/m2, which corresponds to an overestimate of 185% (2.6 dB) for the signal energy and an overestimate of 415% (6.2 dB) for the total record energy. Note that this 2.6 dB signal energy overestimate is 6 dB above the previous −3.4 dB underestimate using filter banks with 1/2 power bandedge overlap. This +6 dB bias may be attributed to spectral leakage, where energy contributions from adjacent filter bands near the bandage frequencies are double-counted (factor of 2 in rms pressure).
With knowledge of this bias, the INFERNO S/N is recomputed using the 0 dB filter bank with a cutoff threshold of S/N > 12 dB to derive a total signal energy estimate of 17.7 J/m2 which overestimates the integrated signal energy by 402% (6 dB). Therefore, filter banks with 0 dB bandedge overlap should not be used in the estimation of signal power, as they will generally overestimate total exposures by ~6 dB.
In summary, care must be taken when applying fractional octave bands to estimate signal power. By restricting energy estimates to those derived from only the most accurate array processing results with high correlation values, total event energy may be underestimated by at least a factor of two (−3 dB). In contrast, bandedge overlapped (0 dB) filter banks may overestimate signal power by a factor of four (+6 dB).
The INFERNO energy estimator using filter banks with 1/2 power bandedge overlap yielded the best match to the signal energy derived from sound pressure integration. The implementation of more refined filter banks (Appendix C) should improve the spectral resolution and accuracy of SPL estimates. Due to window tapering effects, the INFERNO method would tend to underestimate the total energy, whereas direct integration would tend to overestimate due to a lack of disambiguation between signal and noise. A combination of the direct integration and S/N methods in the 5 mHz - 9 Hz frequency band yields an estimated infrasonic signal energy of ~4.2 J/m2, with an error of ~5% for the Russian meteor signal recorded at I31KZ.
To estimate the total equivalent TNT yield at the source would require a source and propagation model, and these considerations are beyond the scope of this work. The multiresolution spectral deconstruction of the meteor trajectory will be the topic of a separate paper.
8. Coda
This work is an invitation to select a common set of standards that meet the scientific requirement of reproducibility, verifiability and precedence. Shared standards not only legitimize research in a field, but also open commercial opportunities by permitting the fair and consistent evaluation of sources, sensors, detection algorithms, and models.
The proposed methods and standards are intended as possible reference points for interdisciplinary collaborations. They may also be complementary to more advanced and adaptable algorithms for signal detection, signature feature recognition, and event characterization.
This methodology is also pertinent to the estimation of exposure levels for active infrasound source characterization and development. With the recent emergence of controllable infrasound sources capable of radiating to 10km ranges and beyond, there will be new applications of active infrasonic soundings for atmospheric studies of large-scale turbulence and variability.
9. Acknowledgements
The author is grateful to A. Smirnoff and ISLA analysts A. Perttu, B. Williams, and N. Badger for their review of the paper and algorithms. In many ways, they are the intended audience. Many thanks to M. Charbit for his detailed review, which strengthened the paper. A. Le Pichon kindly shared early versions of PMCC4, which served as an excellent context for the development and testing of standardized time and frequency bands. L. Liszka provided useful revisions and inspired a recasting of the temporal scaling for convergence with wavelets. J. Olson helped bridge the gap between FFTs and wavelets when he brought to my attention the time frequency uncertainty principle. Early discussions with D. Hart and S. Denis on the need for calibrations standards served as a ground line. This work was supported by the UH Hawaii Institute of Geophysics and Planetology, and I am thankful to P. Mouginis-Mark for his encouragement and support. INFERNO licensing information can be obtained through the UH Office of Technology Transfer and Economic Development.
REFERENCES
- D. R. Christie and P. Campus, “The IMS Infrasound Network: Design and Establishment of Infrasound Stations,” In: A. Le Pichon, E. Blanc and A. Hauchecorne, Eds., Infrasound Monitoring for Atmospheric Studies, Springer, New York, 2010, pp. 29-75. doi:10.1007/978-1-4020-9508-5_2
- A. Le Pichon, E. Blanc and A. Hauchecorne, “Infrasound Monitoring for Atmospheric Studies,” Springer, New York, 2010.
- D. H. Johnson and D. E. Dudgeon, “Array Signal Processing,” Prentice-Hall, Upper Saddle River, 1993.
- C. D. de Groot-Hedlin, M. A. H. Hedlin and K. T. Walker, “Detection of Gravity Waves across the USArray: A Case Study,” Earth and Planetary Sciences Letters, 2013, in review.
- M. A. Garcés, R. A. Hansen and K. Lindquist, “Travel Times for Infrasonic Waves Propagating in a Stratified Atmosphere,” Geophysical Journal International, Vol. 135, No. 1, 1998, pp. 255-263. doi:10.1046/j.1365-246X.1998.00618.x
- D. Brown and M. Garcés, “Ray Tracing in an Inhomogeneous Atmosphere with Winds,” In: D. Havelock, S. Kuwano and M. Vorlander, Eds., Handbook of Signal Processing in Acoustics, Springer, New York, 2008, pp. 1437- 1460. doi:10.1007/978-0-387-30441-0_78
- M. Garcés, C. Hetzer, K. Lindquist, R. Hansen, J. Olson, C. Wilson, D. Drob and M. Picone, “Infrasonic Source Location of the April 23, 2001, Bolide Event,” 23rd Annual DTRA/NNSA Seismic Research Review, Jackson Hole, 1-5 October 2001.
- M. Garcés and C. Hetzer, “Evaluation of Infrasonic Detection Algorithms,” 24th Annual DTRA/NNSA Seismic Research Review, Ponte Vedra, 17-19 September 2002.
- M. Garcés, H. Bass, D. Drob, C. Hetzer, M. Hedlin, A. Le Pichon, K. Lindquist, R. North and J. Olson, “Forensic Studies of Infrasound from Massive Hypersonic Sources,” EOS Transactions, Vol. 85, No. 43, 2004, pp. 433-441. doi:10.1029/2004EO430002
- D. Fee, R. Waxler, J. Assink, Y. Gitterman, J. Given, J. Coyne, P. Maille, M. Garces, D. Drob, D. Kleinert, R. Hofstetter and P. Grenard, “Overview of the 2009 and 2011 Sayarim Infrasound Calibration Experiments,” Journal of Geophysical Research: Atmospheres, 2013. doi:10.1002/jgrd.50398
- M. Garcés and A. Le Pichon, “Infrasound from Earthquakes, Tsunamis and Volcanoes,” In: R. A. Meyers, Ed., Encyclopedia of Complexity and Systems Science, Springer, Berlin, 2009, pp. 663-679.
- A. Le Pichon, L. Ceranna and J. Vergoz, “Incorporating Numerical Modeling into Estimates of the Detection Capability of the IMS Infrasound Network,” Journal of Geophysical Research: Atmospheres, Vol. 117, No. D5, 2012. doi:10.1029/2011JD016670
- American National Standard, “Estimating Air Blast Characteristics for Single Point Explosions in Air, with a Guide to Evaluation of Atmospheric Propagation Effects,” ANSI S2.20-1983 (ASA 20-1983), 1983.
- D. Bolster, R. Hershberger and R. Donnelly, “Dynamic Similarity, the Dimensionless Science,” Physics Today, Vol. 64, No. 9, 2011, 42 p. doi:10.1063/PT.3.1258
- B. J. Merchant and D. M. Hart, “Component Evaluation Testing and Analysis Algorithms,” Sandia Report SAND 2011-8265, Unlimited Release, Sandia National Laboratories, Albuquerque, 2011.
- W. Tempest, “Infrasound and Low Frequency Vibration,” Academic Press, London, 1976.
- Y. Cansi and A. Le Pichon, “Infrasound Event Detection using the Progressive Multi-Channel Correlation Algorithm,” In: D. Havelock, S. Kuwano and M. Vorlander, Eds., Handbook of Signal Processing in Acoustics, Springer, New York, 2008, pp. 1424-1435. doi:10.1007/978-0-387-30441-0_77
- R. S. Matoza, M. Landès, A. Le Pichon, L. Ceranna and D. Brown, “Coherent Ambient Infrasound Recorded by the International Monitoring System,” Geophysical Research Letters, Vol. 40, No. 2, 2013, pp. 429-433. doi:10.1029/2012GL054329
- American National Standard, “Preferred Frequencies, Frequency Levels, and Band Numbers for Acoustical Measurements,” ANSI S1.6-1984 (ASA 53-1984), 1984.
- International Standard on Acoustics, “Frequency-Weighting Characteristics for Infrasound Measurements,” ISO 7196:1995 (E), 1995.
- T. Mikumo, M. Garcés, T. Shibutani, W. Morii, T. Okawa and Y. Ishihara, “Propagating of Acoustic-Gravity Waves from the Source Region of the 2011 Great Tohoku Earthquake (MW = 9.0),” Journal of Geophysical Research: Solid Earth, Vol. 118, No. 4, 2013, pp. 1534-1545. doi:10.1002/jgrb.50143
- J. Marty, D. Ponceau and F. Dalaudier, “Using the International Monitoring System Infrasound Network to Study Gravity Waves,” Geophysical Research Letters, Vol. 37, No. 19, 2010. doi:10.1029/2010GL044181
- J. E. Stopa, K. F. Cheung, H. Tolman and A. Chawla, “Patterns and Cycles in the Climate Forecast System Reanalysis Wind and Wave Data,” Ocean Modeling, 2012, in press. doi:10.1016/j.ocemod.2012.10.005
- American National Standard, “Specification for Octave- Band and Fractional-Octave-Band Analog and Digital Filters,” ANSI S1.11-2004, 2004.
- D. Gabor, “Theory of Communication, Part 3,” Electrical Engineers, Vol. 93, No. 26, 1946, pp. 445-457.
- L. Liszka, “Cognitive Information Processing in Space Physics and Astrophysics,” Pachart Publishing House, Tucson, 2003.
- American National Standard, Measurement of Sound Pressure Levels in Air,” ANSI S1.13-2005 (R 2010), 2010.
- American National Standard, “Guidelines for the Preparation of Standard Procedures to Determine the Noise Emission from Sources,” ANSI S12.1-1983 (ASA 49-1983), 1983.
- American National Standard, “Methods for Measurement of Impulse Noise,” ANSI S12.7-1986 (ASA 62-1986), 1986.
- American National Standard, “Specification for Sound Level Meters,” ANSI S1.4-1983 (ASA 47-1983), 1983.
- J. Chatillon, “Exposure Limits for Infrasounds and Ultrasounds,” Etude bibliographique, INRS-Hygièneetsécurité du Travail-Cahiers de Notes Documentaires-2e Trimester, 2006.
- B. Truax, “The World Soundscape Project’s Handbook for Acoustic Ecology,” Simon Fraser University, and ARC Publications, Vancouver, 1978.
- American National Standard, “Quantities and Procedures for Description and Measurement of Environmental Sound. Part 4: Noise Assessment and Prediction of Long-Term Community Response,” ANSI S12.9-2005/Part 4, 2005.
- M. Niessen, C. Cance and D. Dubois, “Categories for Soundscape: Toward a Hybrid Classification,” Proceedings of Inter Noise, Lisbon, 13-16 June 2010.
- M. A. Garcés, D. Fee and R. Matoza, “Volcano Acoustics,” In: S. A. Fagents, R. M. C. Lopes and T. K. P. Gregg, Eds., Modeling Volcanic Processes: The Physics and Mathematics of Volcanism, Cambridge University Press, Cambridge, 2013, pp. 359-383. doi:10.1017/CBO9781139021562.016
- American National Standard, “Procedures for Outdoor Measurement of Sound Pressure Level,” ANSI S12.18- 1994 (ASA 110-1994), 1994.
- L. E. Kinsler, A. R. Frey, A. B. Coppens and J. V. Sanders, “Fundamentals of Acoustics,” 3rd Edition, John Wiley and Sons, Hoboken, 1982.
- A. D. Pierce, “Acoustics—An introduction to Its Physical Principles and Applications,” 2nd Printing, McGraw-Hill, New York, 1991.
- M. Bahtiarian, “Taking American National Standards to the International Level,” Acoustics Today, Vol. 8, No. 1, 2012, pp. 25-28.
- A. V. Oppenheim and R. W. Schafer, “Discrete-Time Signal Processing,” Prentice Hall, Upper Saddle River, 1989.
- J. R. Bowman, G. E. Baker and M. Bahavar, “Ambient Infrasound Noise,” Geophysical Research Letters, Vol. 32, No. 9, 2005. doi:10.1029/2005GL022486
- J. R. Bowman, G. Shields and M. S. O’Brien, “Infrasound Station Ambient Noise Estimates and Models 2003-2006 (Erratum),” Infrasound Technology Workshop, Brasilia, 2-6 November 2009.
- D. Brown, L. Ceranna, M. Prior, P. Mialle and R. J. Le Bras, “The IDC Seismic, Hydroacoustic, and Infrasound Global Low and High Noise Models,” Pure and Applied Geophysics, 2012. doi:10.1007/s00024-012-0573-6
- A. Le Pichon, L. Ceranna, C. Pilger, P. Mialle, D. Brown, P. Herry and N. Brachet, “2013 Russian Fireball Largest Ever Detected by CTBTO Infrasound Sensors,” Geophysical Research Letters, 2013. doi:10.1002/grl.50619
Notation
c: wave speed (km/s);
l: wavelength (km)
f: wave frequency (Hz);
L: maximum sensor distance (km)
Cel: celerity (nominal 0.21 - 0.34 km/s for infrasound)
R: great circle range (km) from source to receiver Tw: time window length (s)
Twg: Gabor window (s)
fc: center frequency of a filter band (Hz)
lc: center wavelength of a filter band (km)
Tc: center period (s) = 1/fc
f0: reference center frequency of 1 Hz fci: lowest center frequency fcf: highest center frequency Twi: longest time window
Twf: (generally) shortest time window Ts: signal duration, Tw in practice NP: number of center periods NP0: minimum number of periods, Gabor limit NPg: number of Gabor windows M: edge effect compensation coefficient fcut: cutoff frequency for 1/f window scaling N: Bands per octave. N = 1 is a perfect octave, N = 3 yields three bands/octave G: band interval scale, recommend 100.3
n: band number, 
kN: frequency scaling factor, G(1/2N)
f1: lower bandedge frequency, = fcn/kN
f2: upper bandedge frequency, fcnkN
Dfn: bandwidth, f2 − f1
bN1: scaled bandedge bandwidth f1p: lower flat bandpass frequency f2p: upper flat bandpass frequency bN2: scaled bandwidth for flat bandpass NF: number of frequency bands m: alternate frequency band counter, 
prms: root mean square (rms) pressure amplitude (Pa)
pref: reference rms pressure in air, 20 mPa Ts: signal duration (s)
P: power spectral density, Pa2/Hz rc: acoustic impedance, ~400 kg×m−2 s in air I: sound intensity (W×m‒2)
Iref: reference intensity in air, 10‒12 W×m‒2
E: exposure energy (J×m‒2) = ITs
SPL: sound pressure level, dB Ld: sound exposure level, dB NT: number of overlapped, adjacent time windows wp: normalized percent window overlap ti: ith time bin
Appendix A. Nominal Values for PMCC4 Time Windows Using Fractional Octave Bands
Instead of the order number, PMCC4 uses a number counter from 1:NF, where NF is the total number of frequency bands. For an Nth octave specification N and a prescribed minimum and maximum bandpass frequencies fmin and fmax, the order numbers are:
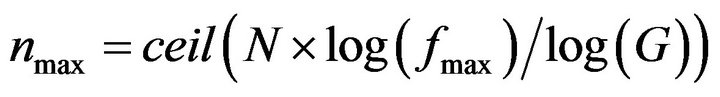
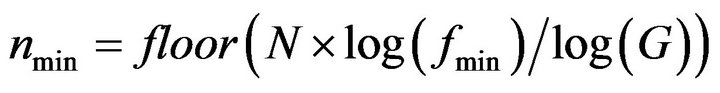
The total number of frequency bins NF are:
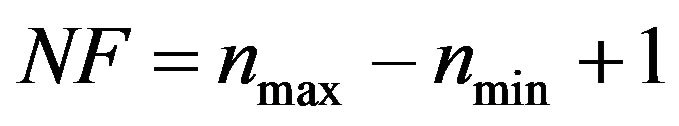
For fractional octave bands (geometric frequency spacing) with 1/f time window scaling, the time window length may be defined by:
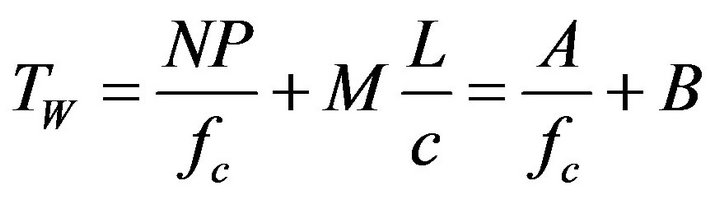
PMCC4 computes the 1/f window length using the expression
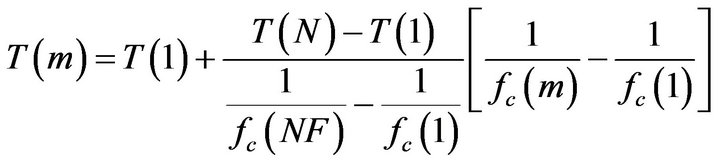
If we use:
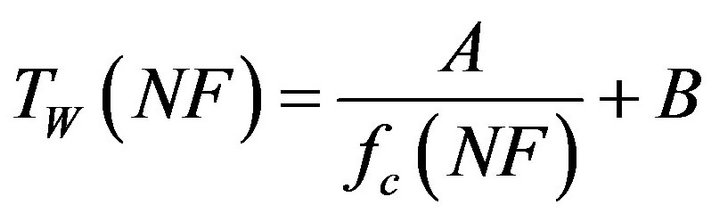
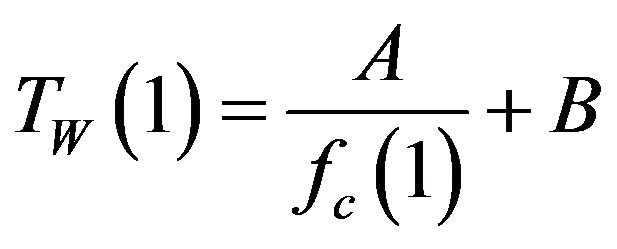

The case of B=0, appropriate when considering very low frequencies, single sensors, networks, or when optimizing windows, yields
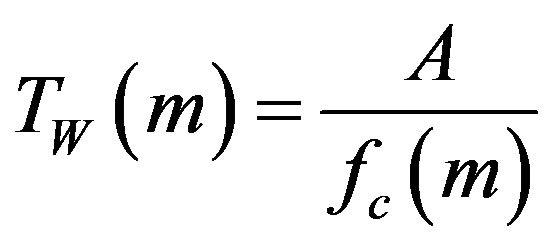
In which case,
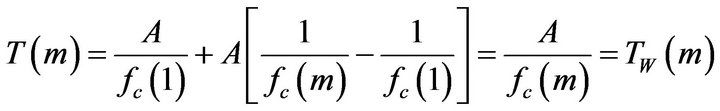
Thus both window types are in agreement with the 1/fPMCC4 window computation schema. This time scaling schema can be used even if the frequencies are linearly distributed.
For a known T(NF) and T(1), A and B (>0) can be recovered from
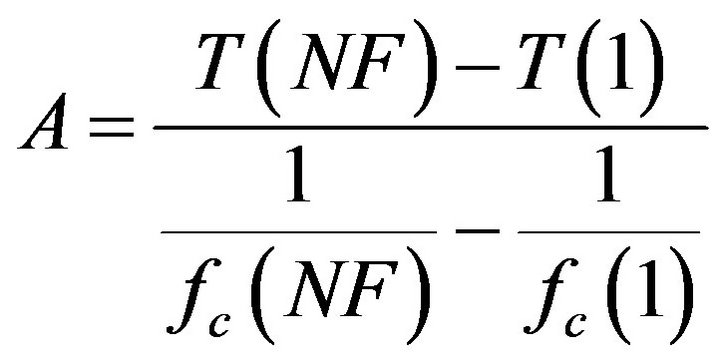
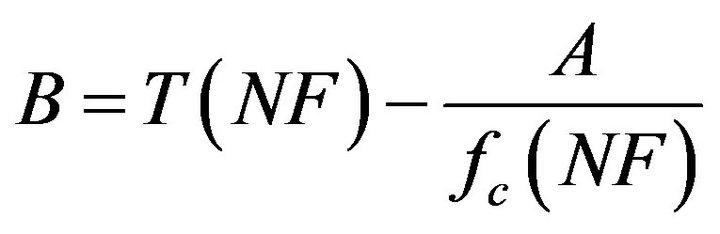
The PMCC4 linear time window scaling is not consistent with the 1/f formulation, and should not be used with these relationships.
Appendix B. PMCC4 Filter Bank Specifications
For the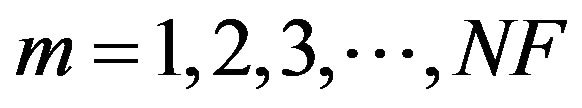 , defined in Appendix A, evenlyspaced bandedge frequencies can be computed from
, defined in Appendix A, evenlyspaced bandedge frequencies can be computed from
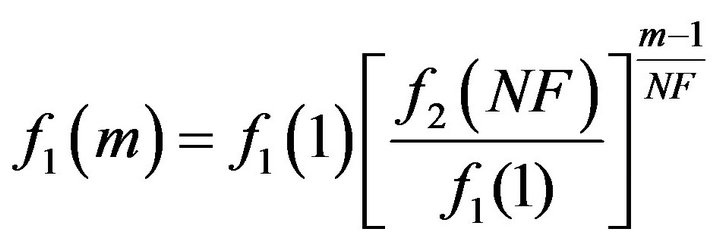
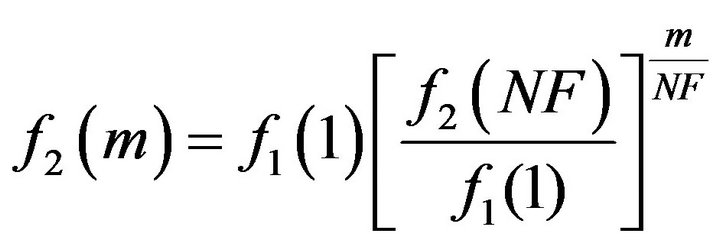
This can be further constrained by using the exact Nth octave frequency band specifications, where
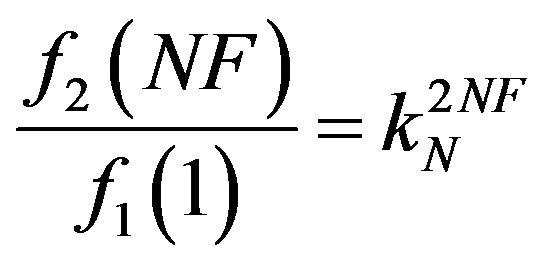
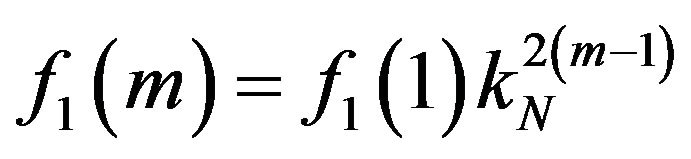
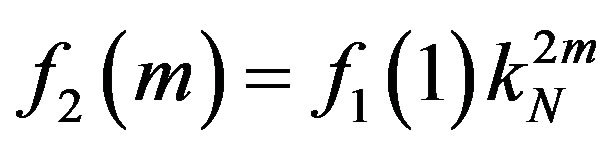
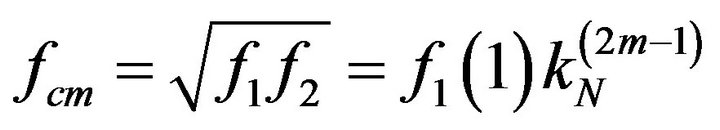
Note that once the Nth octave has been specified in conjunction with the bandpass of interest, the number of bands NF is fixed.
Appendix C. Setting –X dB Filter Bank Bandedge Overlap for the Non-Specialist
When redesigning fractional octave filter banks with an arbitrary degree of overlap, it may be desirable to preserve the center frequency fc and the constant bandwidth b1 relative to the center frequency. There are probably many elegant and mathematically fabulous ways of performing this function. This is not one of them. However, this formulation will permit a simple and rapid evaluation of an arbitrary overlap level for log-space filter banks that preserve the center frequency and constant (scaled) bandwidth properties.
Let f1 and f2 be defined as the –X dB point bandedges for a fractional octave filter with center frequency fc, where
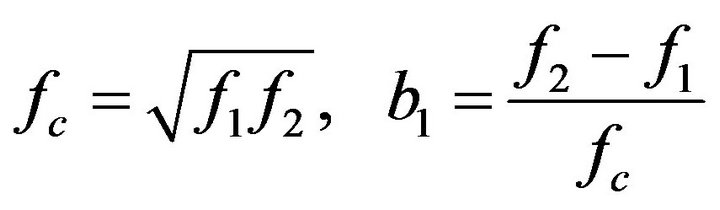
The flat passband (with specified ripple) of a filter [f1p, f2p] can be defined from
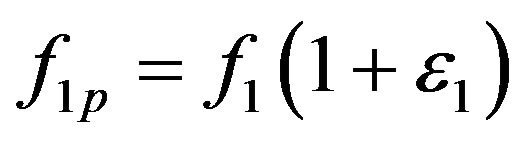 (C1)
(C1)
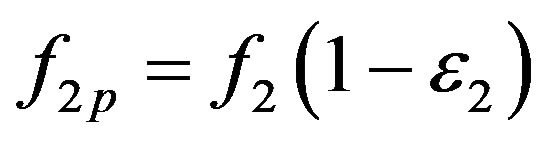 (C2)
(C2)
where . The center frequency should remain invariant, so that
. The center frequency should remain invariant, so that
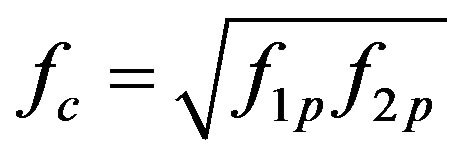 , (C3)
, (C3)
and a new scaled constant (flat) bandwidth b2 can be defined as
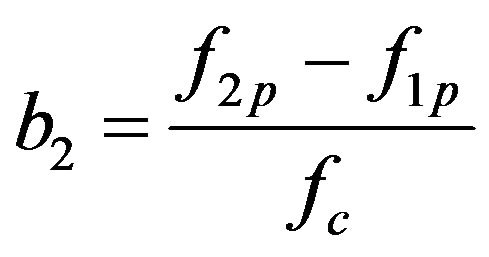 . (C4)
. (C4)
This parametrization sets autoscaling with frequency. Using the general relationship for fractional octave bands,
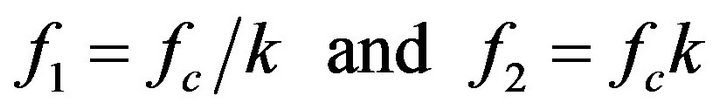 Define b = b2/b1 as the ratio of the flat bandwidth to the bandedge bandwidth, and
Define b = b2/b1 as the ratio of the flat bandwidth to the bandedge bandwidth, and
 ,
, .
.
Application of Equations (C1) and (C2) to Equations (C3)and (C4) yields
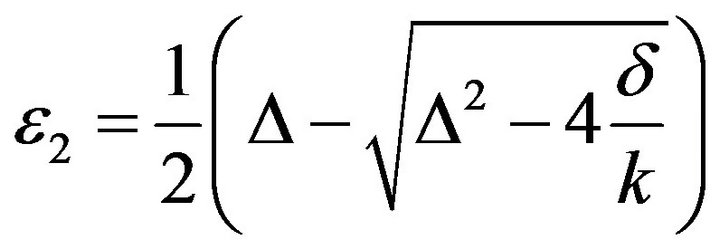 ,
,
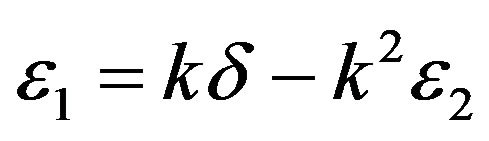 .
.
Since the bandwidth b1 changes with specification of an Nth octave, the variables e1 and e2 will also change accordingly.
If , these expression simplify to:
, these expression simplify to:

Leading to the symmetric solutions for the flat bandpass frequencies,
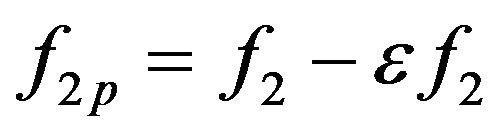
where e is determined by the ratio of the flat passband b2 to the bandedge bandwidth b1. In the case of b = 1, e1 = e2 = 0 and the filter is flat over [f1 f2]. Although the approximate solution is attractive, the exact expressions must be used when coding.
As desired, these solutions autoscale with the center frequency fc. For any desired filter, one can empirically find the value of b that leads to a –X dB intersection point.
Figure C1 shows the filter response for second, third, and fourth order Chebyshev Type I filters with a ripple of 0.01. The second-order filters are the least steep, and
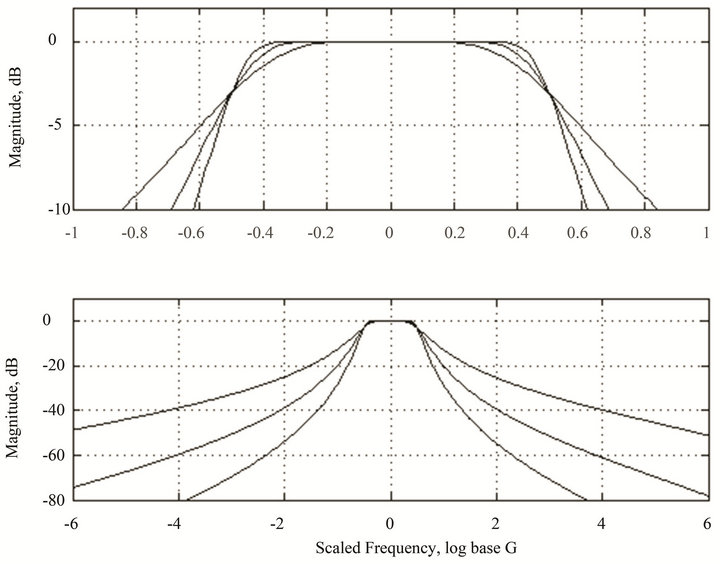
Figure C1.. Filter Response curves for second, third, and fourth order Chebyshev Type I filters with a ripple of 0.01, relative to ANSI S1.11-2004.
are remarkably stable over the broad infrasonic spectrum and sample rates of practical interest, as demonstrated by PMCC in over fifteen years of applications. Numerical tests over various fractional octave bands show that the −3 dB point for the second-order filter banks is at b ~ 0.3, which means that only ~30% of the passband has a flat response (Figure C1). As discussed in Section 7, adjacent filter bands that intersect at the −3dB points deliver better spectral resolution, reduce spectral leakage, and are more compliant with ANSI standards. However, the second-order Chebyshev Type I filter specifications do not meet ANSI [24] Class 2 minimum and maximum specifications, as they drop off too fast in the passband and then drop off too slowly past the bandedges. For third order Chebyshev Type I filter specifications, the −3dB edge band levels are found at b = 0.53, and for fourth order, at b = 0.68 (Figure C1). The third order filters would almost meet the Class 2 specifications, and it appears fourth order filters would meet Class 0 specs as defined in [24]. However, higher-order filters can be unstable without careful design and testing using the passband and sampling rates of interest.
As in audio acoustics, once the filter bands are agreed upon it is possible to construct stable, custom-designed filter banks that will meet ANSI specifications, or their adequate extension into the infrasound range.

