International Journal of Modern Nonlinear Theory and Application
Vol.04 No.04(2015), Article ID:61037,11 pages
10.4236/ijmnta.2015.44016
Numerical Simulation of Reaction-Diffusion Systems of Turing Pattern Formation
Gendai Gu, Hongxiao Peng
School of Mathematics and Physics, North China Electrical Power University, Baoding, China

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 7 October 2015; accepted 9 November 2015; published 12 November 2015

ABSTRACT
Differential method and homotopy analysis method are used for solving the two-dimensional reaction-diffusion model. And the structure of the solutions is analyzed. Finally, the homotopy series solutions are simulated with the mathematical software Matlab, so the Turing patterns will be produced. Overall analysis and experimental simulation of the model show that the different parameters lead to different Turing pattern structures. As time goes on, the structure of Turing patterns changes, and the final solutions tend to stationary state.
Keywords:
Differential Method, Homotopy Analysis Method, Reaction-Diffusion Model, Turing Patterns

1. Introduction
In time or space, patterns have nonuniform macroscopic structure with regularity. From the thermodynamic point of view, the nature of the pattern formation can be divided into two categories. One is presenting in the thermodynamic equilibrium conditions, such as the crystal structure of inorganic chemistry, the self-organic pattern formation of organic polymers and so on. The other is the station far from the thermodynamic equilibrium conditions, such as the ripples of the sea, the surface patterns of the animal, the strip clouds in the sky and so on.
Reaction-diffusion system is one of the fundamental equations which describe the motion of the nature. It not only has a wide practical background, but also is used in many fields, for example, predator-prey model, spread of infectious diseases, migration of population and spread of forest fires. Its mathematical model is a special kind of parabolic partial differential equations. As for reaction-diffusion systems, the coupling of nonlinear dynamical and linear diffusion leads to spontaneously producing a variety of ordered or disordered pattern of the system. This is the pattern dynamics of the reaction-diffusion systems [1] . According to the pattern dynamics, the ordered patterns can be divided into two categories: stationary state (such as Turing patterns) and traveling wave (such as spiral pattern). As for the Turing patterns of reaction-diffusion systems, in 1952, Turing [2] for the first time showed that the homogeneous system will be stable with little disturbance for the absence of proliferation, while it becomes unstable with the spatial disturbance for joining the steady-state diffusion. This is the Turing instability of reaction-diffusion equations.
The classical method to study the Turing patterns of reaction-diffusion is the analysis of linear stability method [3] - [8] . Firstly, the nonlinear reaction-diffusion model is turned into linear model. Then, perturbation theory is utilized to study its solution which can be seen as the little perturbation of equilibrium state (i.e. uniform and stable state). And we can obtain the conditions of generating Turing pattern through studying the linear equations with perturbation by the analysis of stability method. Finally, through the numerical simulation, the reaction-diffusion model can obtain different Turing pattern structures. This method shows the relationship between the parameters of generating Turing pattern. But for the strong nonlinear problems, this method may not be applicable.
The range of parameters of the Turing pattern can be obtained by the analysis of linear stability method. Based on the parameters which limit to the range, this article solves the reaction-diffusion model by the use of the combination of differential method and homotopy analysis method. Then the changes of the mechanism of Turing patterns can be under control by the simulation of experimental data and analysis of utilizing this method. Finally, the study of the concrete case shows the feasibility and effectiveness of this method.
2. Homotopy Analysis Solution of Reaction-Diffusion Model
The general mathematical representation of two-dimensional reaction-diffusion model is as follows,
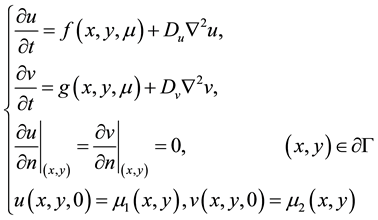 (1)
(1)
Their definition are as follows: u and v are different reactant concentrations vector;
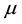 is a control parameter; f and g represent the nonlinear dynamics function of the system;
is a control parameter; f and g represent the nonlinear dynamics function of the system;
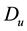 and
and
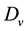 describe the diffusion coefficient;
describe the diffusion coefficient;
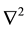 is Laplace operator;
is Laplace operator;
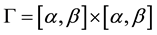 describes the regional space of the research for the model.
describes the regional space of the research for the model.
Discrete the reaction-diffusion model in discrete nodes
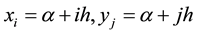
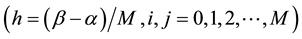 . The discretization of the model takes the following form,
. The discretization of the model takes the following form,
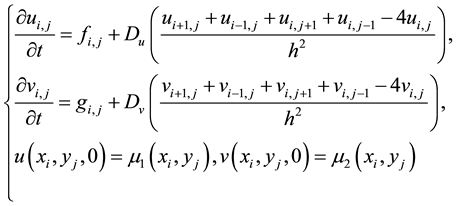 (2)
(2)
And,
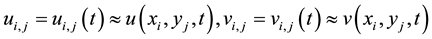 (3)
(3)
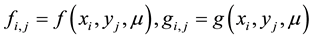 (4)
(4)
According to the thought of homotopy analysis method, we take the value
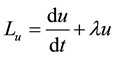 , (5)
, (5)
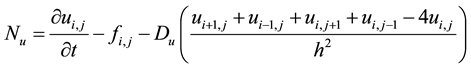 (6)
(6)
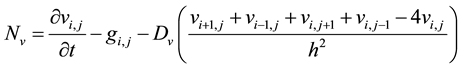 (7)
(7)
and impose the initial guess solutions
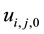 and
and










The problem (8) shows that two cases. One is




are continuous from initial guess solutions







where



The two sides of zero-order Equations (8) are solved m-order derivative about q and divided



where
The solutions of problem (10) are,

Choose the auxiliary function

In order to make Taylor series are convergent at


In summary, the m-order homotopy approximate solutions of problem (1) are

3. Solving of Example and Analysis
3.1. Homotopy Analysis of Brusselator Reaction Diffusion Model
The typical Brusselator reaction diffusion model is as follows,

where









el and the steady-state solution of the homogeneous perturbation analysis, the guess of initial solution can be as follows,

where




where



Brusselator model is a classical dissipative structure model, which has been studied by many researchers. The conditions for Turing bifurcation of Brusselator model is as follows,

3.2. The Effective Range of h
Parameters






Figure 1. The effective area about


Figure 2. The effective area about


Figure 3. The effective area about


Figure 4. The effective area about


Table 1. The effective area about

3.3. Simulation of Turing Patterns about Reaction-Diffusion
Parameter





Figure 5. The patterns in space of u(t), when t = 0.1.
Figure 6. The patterns in space of v(t), when t = 0.1.
Figure 7. The patterns in space of u(t), when t = 0.5.
Figure 8. The patterns in space of v(t), when t = 0.5.
Figure 9. The patterns in space of u(t), when t = 1.
Figure 10. The patterns in space of v(t), when t = 1.
Figure 11. The patterns in space of u(t), when t = 10.
Figure 12. The patterns in space of v(t), when t = 10.
The parameters


As time goes on, the final pattern structure will tend to a steady state. Turing patterns structure of homotopy series solutions are sensitive to the selection of initial guess solution and are affected by the wave number. In summary, in the range of parameter about Turing patterns, the system will appear striped patterns, point patterns and the coexistence of striped and point pattern with the time going on.
Figure 13. The patterns in space of u(t), when t = 0.1.
Figure 14. The patterns in space of v(t), when t = 0.1.
Figure 15. The patterns in space of u(t), when t = 0.5.
Figure 16. The patterns in space of v(t), when t = 0.5.
Figure 17. The patterns in space of u(t), when t = 1.
Figure 18. The patterns in space of v(t), when t = 1.
Figure 19. The patterns in space of u(t), when t = 10.
Figure 20. The patterns in space of v(t), when t = 10.
4. Conclusions
In this paper, a new method based on differential method and homotopy analysis method is used to solve the typical two-dimensional reaction diffusion model. Different shapes of Turing pattern can be obtained through Matlab mathematical software on experimental data simulation of the structure of the solution. And it is proved that the proposed method which to solving nonlinear reaction diffusion problems is feasible and effective. The new method not only reduces the dimension about differential in space, but also gets the analytical expression with physical parameters through the homotopy in time. It will facilitate the analysis of the influence of parameters variation on Turing pattern structure. The method which is differential in space and homotopy in time domain has enormous potential for solving definite solution of nonlinear partial differential, and it has great promotional value.
The innovation point of this article is making use of the new method to solve the two-dimensional reaction diffusion model. The new method is combining the differential method and homotopy analysis method.
Funding
This work is supported by the National Sciences Foundation of People’s Republic of China under Grant 1140011526.
Cite this paper
GendaiGu,HongxiaoPeng, (2015) Numerical Simulation of Reaction-Diffusion Systems of Turing Pattern Formation. International Journal of Modern Nonlinear Theory and Application,04,215-225. doi: 10.4236/ijmnta.2015.44016
References
- 1. Ouyang, Q. (2010) Nonlinear Science and Pattern Dynamics. Peking University Press, Beijing.
- 2. Ouyang, Q. (2000) Reaction Diffusion System Pattern Dynamics. Shanghai Science and Technology Education Press, Shanghai.
- 3. Liu, P.P. (2009) A Ratio Dependent Predator-Prey Model of Spatial Pattern Formation Research. Mathematics in Practice and Theory, 39, 114-119.
- 4. Wang, Y., Cao, J.D., Sun, G.-Q. and Li, J. (2014) Effect of Time Delay on Pattern Dynamics in a Spatial Epidemic Model. Physica A: Statistical Mechanics and Its Applications, 412, 137-148.
http://dx.doi.org/10.1016/j.physa.2014.06.038 - 5. Parshad, R.D., Kumari, N., Kasimov, A.R. and Abderrahmane, H.A. (2013) Turing Patterns and Long-Time Behavior in a Three-Species Food-Chain Model. Mathematical Biosciences, 254, 83-102.
http://dx.doi.org/10.1016/j.mbs.2014.06.007 - 6. Liu, S.H. and Gu, Y.X. (2012) Coupled Reaction-Diffusion System in the Superlattice Pattern. Hebei University (Natural Science Edition), 32, 597-601.
- 7. Du, Y.-K. and Xu, R. (2014) Pattern Formation in Two Classes of SIR Epidemic Models with Spatial Diffusion. Chinese Journal of Engineering Mathematics, 31, 454-462.
- 8. Li, X.Z., Bai, Z.G., Li, Y., Zhao, K. and He, Y.F. (2013) Double Nonlinear Coupling Reaction-Diffusion Systems in Complex Turing Patterns. Chinese Journal of Physics, 62, 220503-1 -220503-7.









































