Received 27 February 2015; accepted 10 May 2015; published 15 May 2015

ABSTRACT

This paper proposes an output feedback nonlinear general integral controller for a class of uncertain nonlinear system. By solving Lyapunov equation, we demonstrate a new proposition on Equal ratio gain technique. By using Equal ratio gain technique, Singular perturbation technique and Lyapunov method, theorem to ensure regionally as well as semi-globally exponential stability is established in terms of some bounded information. Moreover, a real time method to evaluate the ratio coefficients of controller and observer are proposed such that their values can be chosen moderately. Theoretical analysis and simulation results show that not only output feedback nonlinear general integral control has the striking robustness but also the organic combination of Equal ratio gain technique and Singular perturbation technique constitutes a powerful tool to solve the output feedback control design problem of dynamics with the nonlinear and uncertain actions.

Keywords:

General Integral Control, Nonlinear Control, Robust Control, Output Feedback Control, Equal Ratio Gain Technique, Singular Perturbation Technique, State Estimation, Integral Observer, Output Regulation

1. Introduction

Integral control [1] plays an important role in practice because it ensures asymptotic tracking and disturbance rejection when exogenous signals are constants or planting parametric uncertainties appear. However, output feedback nonlinear general integral control design is not a trivial matter because it depends on not only the uncertain nonlinear actions, disturbances and nonlinear control actions but also the uncertain estimation error dynamics. Therefore, it is of important significance to develop the design method for output feedback nonlinear general integral control since some states cannot be measured in practice.

For general integral control design, there were various design methods, such as general integral control design based on linear system theory, sliding mode technique, feedback linearization technique and singular perturbation technique and so on, which were presented by [2] -[5] , respectively. In addition, general concave integral control [6] , general convex integral control [7] , constructive general bounded integral control [8] and the generalization of the integrator and integral control action [9] were all developed by using Lyapunov method and resorting to a known stable control law. Equal ratio gain technique firstly was proposed by [10] and was used to address the linear general integral control design. After that Equal ratio gain technique was extended to the canonical interval system matrix [11] and was used to deal with nonlinear general integral control design. All these design methods and general integral controls above are all based on the state feedback. Presently, output feedback general integral control along with its design method has not been developed.

Motivated by the cognition above, this paper proposes an output feedback nonlinear general integral controller for a class of uncertain nonlinear system. The main contributions are that: 1) as any row integrator and its controller gains of a canonical interval system matrix tend to infinity with the same ratio, if it is always Hurwitz, and then the same row solutions of Lyapunov equation all tend to zero; 2) theorem to ensure regionally as well as semi-globally exponential stability is established in terms of some bounded information; 3) a real time method to evaluate the ratio coefficients of controller and observer are proposed such that their values can be chosen moderately. Moreover, theoretical analysis and simulation results show that not only output feedback nonlinear general integral control has the striking robustness but also the organic combination of Equal ratio gain technique and Singular perturbation technique constitutes a powerful tool to solve the output feedback control design problem of dynamics with the nonlinear and uncertain actions.

Throughout this paper, we use the notation 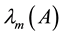and 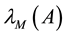to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive define bounded matrix, for any. The norm of vector x

is defined as, and that of matrix A is defined as the corresponding induced norm.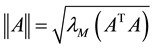

The remainder of the paper is organized as follows: Section 2 describes the system under consideration, assumption and output feedback nonlinear general integral control. Section 3 demonstrates a new proposition on Equal ratio gain technique. Section 4 addresses the design method. Examples and simulation are provided in Section 5. Conclusions are presented in Section 6.

2. Problem Formulation

Consider the following controllable nonlinear system,

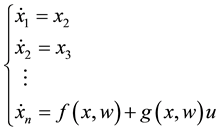(1)

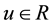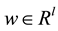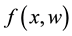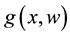where is the state; is the control input; is a vector of unknown constant parameters and disturbances. The uncertain nonlinear functions and are all continuous in on the control domain. We want to design an output feedback control law such that 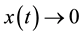as.

Assumption 1: There is a unique pair that satisfies the equation,

(2)

so that is the desired equilibrium point and is the steady-state control that is needed to maintain equilibrium at, irrespective of the value of.

Assumption 2: Suppose that the functions and satisfy the following inequalities,

(3)

(4)

(5)

(6)

for all and, where, , , and are all positive constants.

For the purpose of this paper, it is convenient to introduce the following definition.

Definition 1: with, , and denotes the set of all continuous differential increasing function [12] , , such that

,

where stands for the absolute value.

Figure 1 depicts the example curves for the functions belonging to the function set. For instance, for all, the functions, , , , , and so on, all belong to function set.

The output feedback nonlinear general integral controller [11] and observer [12] are given as,

(7)

(8)

where is the estimated state; is the prescient constant parameters and disturbances;, , and are all positive constants;

,

,

and are the slopes of the line segment connecting to the origin; is used to attenuate the uncertain nonlinear action of; is applied to reorganize the integrator output; is utilized to improve the integral control per-

formance; and are the normal models of and

, respectively. belongs to the function set.

Assumptions 3: By the definition of controller (7), it is convenient to suppose that the following inequalities,

(9)

(10)

hold for all, and, , where and are all positive constants.

By the definitions of, and, and letting , the controller (7) can be written as,

(11)

and the whole closed-loop system can be written as,

(12)

(13)

where

, ,

and is integrated into.

By the equation (2) and inequality (4), and choosing and to be large enough, and then setting and of the systems (12) and (13), we obtain

(14)

(15)

where

and.

Thus, we ensure that and are the unique solutions of the systems (12) and (13), respectively.

Defining, and , and substituting (14)

and (15) into (12) and (13), respectively, the whole closed-loop system can be rewritten as,

(16)

where

,

,

,

,

,

,

,

,

,

and is integrated into and.

By Assumptions 2 and 3, the uncertain terms, , , and satisfy the linear growth bound,

(17)

(18)

(19)

(20)

(21)

where, , , , , , and are all positive constants.

3. Propositions on Equal Ratio Gain Technique

Equal ratio gain technique is firstly proposed by [10] and is extended to the canonical interval system matrix in [11] . For analyzing the stability of the closed-loop system (16), it is necessary to review two important propositions on Equal ratio gain technique as follows.

Proposition 1 [10] : as any row controller gains, or controller and its integrator gains of a canonical system matrix tend to infinity with the same ratio, if it is always Hurwitz, and then the same row solutions of Lyapunov equation all tend to zero.

Proposition 2 [11] : a canonical interval system matrix can be designed to be Hurwitz as any row controller gains, or controller and its integrator gains increase with the same ratio.

Based on two Propositions above, it is not enough to analyze the stability of the closed-loop system (16). So, a new proposition on Equal ratio gain technique is demonstrated in the next two subsections.

3.1. New Proposition

Consider the following controllable canonical interval system matrix A,

where

,

,

and is a positive constant.

By Proposition 2, the interval system matrix A can be designed to be Hurwitz for all, and. Thus, for any given positive define symmetric matrix Q there exists a unique positive define symmetric matrix P that satisfies Lyapunov equation, and the solution of Lyapunov equation can be obtained by skew symmetric matrix approach [13] , that is,

where

and.

The inversion of the matrix A with is,

(22)

where the elements are omitted since it is useless to achieve our object. The interesting reader can evaluate them by.

It is well known that the solution P of Lyapunov equation is more and more complex as the order of the system matrix A increases. Therefore, for clearly showing the results, we consider a simple case, that is, taking and of the system matrix A. Thus, taking, obtain,

where

and then we have,

Now, , , , and are multiplied by, then we obtain,

It is obvious that, and all tend to the constants as, and then we have,

as

where.

From the statements above, it is easy to see that for of the system matrix A, can be formulated as the linear form on and tends to zero as. Moreover, the solution of the matrix S is more and more complex as the order of the system matrix A increases. Thus, by the inversion of system matrix (22), can be formulated as the linear form on for the -order system matrix A, and with the help of computer, it can be verified that the solution of still tends to the constant as. Therefore, for the -order system matrix A, we can conclude that as. As a result, the following theorem can be established.

Theorem 1: If the interval system matrix A is Hurwitz for all, and, and then we have,

as.

where

,

.

Discussion 1: From the statements above, the solution of the matrix S is more and more complex as the order of the system matrix A increases. So, although Theorem 1 is demonstrated by taking and the single variable system matrix A, it is very easy to extend Theorem 1 to any given positive define symmetric matrix Q and the multiple variable system matrix A with the help of computer since there is not any difficulty to obtain the solution of the matrix S in theory, that is, Lyapunov equation applies to not only the single system matrix but also the multiple system matrix. Thus, there is the following proposition.

Proposition 3: as any row integrator and its controller gains of a canonical interval system matrix tend to infinity with the same ratio, if it is always Hurwitz, and then the same row solutions of Lyapunov equation all tend to zero.

3.2. Example

For testifying the justification of Theorem 1 and Proposition 3, we consider a 6-order two variable system matrix A as follows,

The inversion of the system matrix A is,

where

By the equation, it is very easy to obtain the fifteen linear equations with fifteen elements of the matrix S. So, it is omitted.

Thus, taking

.

Now, by Routh’s stability criterion and with the help of computer, we have: 1) if and of the system matrix A are multiplied by, then it is still Hurwitz for all, and the numerical solutions of are shown in Table 1; 2) if and of the system matrix A are multiplied by, then it is still Hurwitz for all, and the numerical solutions of are shown in Table 2.

From the example above, it is obvious that: 1) as shown in Table 1, Table 2, the absolute values of and are all decrease as reduces; 2) although the result above is obtained by a constant system matrix, it is easy to be extended to the interval system matrix. This not only verifies the justification of Theorem 1 and Proposition 3 but also shows that for the high order and multiple variable system matrix, it is convenient and practical with the help of computer.

4. Stability Analysis

The asymptotic stability of the closed-loop system (16) can be achieved by Equal ratio gain technique and Singular perturbation technique as follows:

By Proposition 2 [11] , the interval system matrix can be designed to be Hurwitz for all

, , and,

and by choosing , the matrix can be designed to be Hurwitz, too. Thus, by linear system theory, two quadratic Lyapunov functions,

(23)

(24)

can be obtained. Where and are the solutions of Lyapunov equations,

and

with any given positive define symmetric matrices and, respectively.

Using [1] as Lyapunov function candidate, and then its time derivative along the trajectories of the closed-loop system (16) is,

(25)

Substituting and into (25), obtain,

(26)

where

,

,

.

Now, by Propositions 1 and 3, we have,

as,

as.

Substituting them and (17) - (21) into (26), obtain,

(27)

where

,

,

,

,

,

,

.

The right-hand side of the inequality (27) is a quadratic form, which is negative define when,

(28)

This is equivalent to,

(29)

By the dependence of on, it is obvious that the maximum of occurs at [1] and is given by,

(30)

Although and are dependent on, they are fixed for any given moment and all tend to the constants as, and then there exists such that holds for all. Thus, by choosing a moderate and solving the Equation (30), can be obtained, and then holds for all and. Consequently, if holds for all, then we conclude that holds uniformly in.

Using the fact that Lyapunov function is a positive define function and its time derivative is a negative define function if holds for all, we conclude that the closed-loop system (16) is stable. In fact, means, , and. By invoking LaSalle’s invariance principle, it is easy to know that the closed-loop system (16) is uniformly exponentially stable. As a result, we have the following theorem.

Theorem 2: Under Assumptions 1, 2 and 3, if the matrix is Hurwitz and the interval system matrix is Hurwitz for all, , and, and then the equilibrium point, , and of the closed-loop system (16) is uniformly exponentially stable for all and. Moreover, if all assumptions hold globally, and then it is globally uniformly exponentially stable.

By the demonstration above, there exist and such that and hold for all. So, it is practical and feasible to find a real method to evaluate the instantaneous values and, that is, as follows:

Step 1: by the inequality, the impermissible minimum of is,

Step 2: by the definitions of and, the instantaneous values and can be given as,

Step 3: by the values, , and the condition, and using the iterative method to solve Lyapunov equation,

can be obtained. Thus, by choosing a moderate and solving Lyapunov equation above again, and can be evaluated.

Step 4: by the values, and definitions of, , , and, , , , , , , and can be obtained for given. can be evaluated by solving Lyapunov equation.

Step 5: by the values, , , , , , , , , and

, and using the iterative method to solve the inequality (30), can be obtained.

Discussion 2: From the procedure of stability analysis above, it is obvious that: although is dependent on, can be chosen arbitrarily small. Thus, so long as the bounded conditions (17) - (21) are satisfied, the asymptotically stable control can be achieved. This shows that the striking feature of output feedback nonlinear general integral control, that is, its robustness with respect to the nonlinearities, uncertainties and disturbances from the real system, control input and estimated error dynamics, is clearly demonstrated by Equal ratio gain technique and Singular perturbation technique. This means that the organic combination of Equal ratio gain technique and Singular perturbation technique constitutes a powerful tool to solve the output feedback control design problem of dynamics with the nonlinear and uncertain actions.

5. Example and Simulation

Consider the pendulum system [1] described by,

where, is the angle subtended by the rod and the vertical axis, and T is the torque applied to the pendulum. View T as the control input and suppose we want to regulate to r. Now, taking, , the pendulum system can be written as,

and then it can be verified that is the steady-state control that is needed to maintain equilibrium at the origin.

The nonlinear general integral controller and the integral observer can be given as,

Thus, it is easy to obtain, , , and, and then the closed-loop system can be written as,

where

,

,

,

,

,

,

,

,

,

,

,

,

.

The normal parameters are and, and in the perturbed case, and are reduced to 1 and 5, respectively, corresponding to double the mass. Thus, with, , , , , and, the following inequality,

holds for all, and then the matrix is Hurwitz for all, , , , and, and is Hurwitz, too.

Now, solving Lyapunov equation, , obtain, and using, , , , obtain,

,

,

,

,

,

and then, we have,

, ,

, ,

, ,

,.

Thus, using, , , , , , and to solve the equations,

and, can be obtained.

Now, taking and, the simulation is implemented under the normal and perturbed cases, respectively.

Normal case: the initial states are and; the system parameters are and.

Perturbed case: the initial states are, and; the system parameters are, and, corresponding to doubling of the mass. Moreover, we consider an additive impulse-like disturbance of magnitude 60 acting on the system input between 3 s and 3.5 s.

Figure 2 and Figure 3 showed the simulation results under the normal (solid line) and perturbed (dashed line) cases. The following observations can be made: 1) as, there exists such that and

hold for all, , and. This shows that the closed-loop system is uniformly asymptotic stable. 2) the optimum responses are almost identical before the additive impulse-like disturbance appears. This means that by Equal ratio gain technique and Singular perturbation technique, we can tune an output feedback nonlinear general integral controller with good robustness and high control performance. All these demonstrate that output feedback nonlinear general integral control has the striking robustness, that is, so long as the bounded conditions are satisfied, the asymptotically stable control can be achieved, but also the organic combination of Equal ratio gain technique and Singular perturbation technique constitutes a powerful and practical tool to solve the output feedback control design problem of dynamics with the nonlinear and uncertain actions.

6. Conclusions

This paper proposes an output feedback nonlinear general integral controller for a class of uncertain nonlinear system. The main contributions are that: 1) as any row integrator and its controller gains of a canonical interval system matrix tend to infinity with the same ratio, if it is always Hurwitz, and then the same row solutions of Lyapunov equation all tend to zero; 2) theorem to ensure regionally as well as semi-globally exponential stability is established in terms of some bounded information; 3) a real time method to evaluate the ratio coefficients of controller and observer are proposed such that their values can be chosen moderately.

Theoretical analysis and simulation results show that not only output feedback nonlinear general integral control has the striking robustness but also the organic combination of Equal ratio gain technique and Singular perturbation technique constitutes a powerful tool to solve the output feedback control design problem of dynamics with the nonlinear and uncertain actions.

References