International Journal of Modern Nonlinear Theory and Application
Vol.04 No.01(2015), Article ID:54142,8 pages
10.4236/ijmnta.2015.41001
Impulsive Synchronization of Hyperchaotic Lü Systems with Two Methods
Mingjun Wang
School of Information Engineering, Dalian University, Dalian, China
Email: wmjhome@163.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 January 2015; accepted 11 February 2015; published 16 February 2015
ABSTRACT
In the paper, impulsive synchronization of two hyperchaotic Lü systems with different initial conditions is studied. The sufficient conditions on feedback strength and impulsive distances are established from two different angles to guarantee the synchronization. The relevant theoretical proofs are presented. Numerical simulations show the effectiveness of the methods.
Keywords:
Impulsive Synchronization, Impulsive Distance, Hyperchaotic Lü System, Largest Lyapunov Exponent

1. Introduction
In 1990, Pecora and Corroll proposed the conception of chaotic synchronization and they presented a chaos synchronization method through investigating synchronization of Newcomb circuit [1] [2] . Since chaos control and synchronization have great potential applications in many areas such as information science, medicine, biology and Engineering, they have received a great deal of attention. Numerous researches have been done theoretically and experimentally [3] - [6] . Many approaches have been proposed for chaos synchronization, including feedback method, adaptive synchronization, impulsive synchronization and fuzzy synchronization method [7] - [12] . Because of transmitting signals in discrete times, impulsive synchronization demands less energy. Besides, it has faster synchronous speed than other methods. It is more practical in practical applications. Recently, many efforts have been devoted to impulsive synchronization. Ren et al. proposed impulsive synchronization of cou- pled chaotic systems via adaptive-feedback approach [13] . Chen et al. proposed a synchronization method of a class of chaotic systems using small impulsive signal [14] . Xi et al. presented adaptive impulsive synchronization for a class of fractional-order chaotic and hyperchaotic systems [15] . Xu et al. studied a new chaotic system without linear term and its impulsive synchronization [16] . In the paper, impulsive synchronization of hyperchaotic Lü system is studied. Based on the boundedness and the largest Lyapunov exponent, two different sufficient conditions are established to guarantee the synchronization. These two methods are analyzed and compared. Numerical simulations show the effectiveness of these methods.
2. Impulsive Synchronization Theory
Suppose a  -dimensional chaotic system as
-dimensional chaotic system as
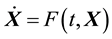 (1)
(1)
choose system (1) as drive system, response system is as follows
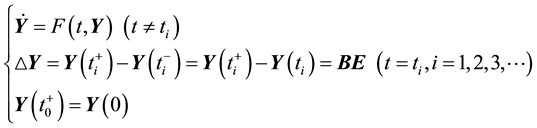 (2)
(2)
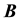 is a matrix which stands for a linear combination of
is a matrix which stands for a linear combination of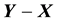 , let
, let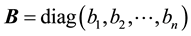 ; The error vector is
; The error vector is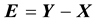 ;
; 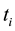 is the discrete time at which the impulse is transmitted. According to system (1) and system (2), we can get the error system
is the discrete time at which the impulse is transmitted. According to system (1) and system (2), we can get the error system
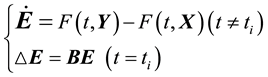 (3)
(3)
Suppose the impulsive distance 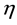 is invariable,
is invariable, 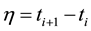 , if we can obtain
, if we can obtain 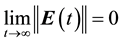 under some-
under some-
conditions, system (1) and system (2) can be synchronized by impulses. Next we will take hyperchaotic Lü system as example for detailed description.
3. Implement of Impulsive Synchronization
3.1. Description of Hyperchaotic Lü System
Hyperchaotic Lü system [17] is described as
 (4)
(4)
in this paper choose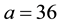 ,
, 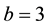 ,
, 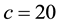 and
and 

Figure 1. The projections of hyperchaotic Lü system’s attractor.
Choose hyperchaotic Lü system

as drive system. System (5) can be described as

where
The response system is described as

where
The error system is

where
Next the sufficient conditions on feedback strength and impulsive distances will be established from two different angles to guarantee the synchronization.
3.2. Based on the Boundedness of Chaotic System
Theorem 1 Suppose










then system (6) and system (7) can be synchronized.
Proof: Choose Lyapunov function as

Calculate the derivative of Equation (10), yield

When

When

Let


When

From Equation (13) and Equation (15),

According to Equation (12), when

In the same way, when

From Equation (9), yield

hence

Substitute Equation (20) into Equation (18), we can obtain when

Since



From Figure 1, we can choose


Suppose Equation (9) can be satisfied, then








In this numerical simulation, let

Equation (7). The initial states of the drive system (6) and the response system (7) are taken as 












3.3. Based on the Largest Lyapunov Exponent of Chaotic System
Theorem 1 provides sufficient condition for the synchronization of system (6) and system (7), but Equation (9) is not necessary condition. Through simulations we find that the above condition is too rigorous. In fact the qualified impulsive distance can be much larger than 


Figure 2. (Based on boundedness) Synchronization error system (8) states:



Suppose the initial distance between system (6) and system (7) is
system(6) is


time of the chaotic system is 
Theorem 2 Suppose 









System (6) and system (7) can be synchronized
Proof: Suppose

then

hence




In the same way, we have

According to the condition of Theorem 2:

According to Equation (29) and Equation (30), we obtain

Here, we still choose




have








In this numerical simulation, let

Equation (7). The initial states of the drive system (6) and the response system (7) are taken as 


shows the history of











Figure 3. (Based on the largest Lyapunov exponent) Synchronization error system (8) states:



3.4. Comparison of Two Methods
If system (6) and system (7) achieve synchronization, system (8) will be steady at zero. Suppose



From Figure 4 and Figure 5, we can see that the requirement of impulsive distance in Theorem 1 is more rigorous than Theorem 2. Comparing the methods of Theorem 1 and Theorem 2, the former is based on the boundedness of chaotic system, it considers the extreme case all the time, while the latter is based on the largest Lyapunov exponent of chaotic system, it represents the average case. Therefore, the sufficient condition in Theorem 1 is a very small part of the condition in Theorem 2. Of course, in view of the requirements of synchronous time and quality, it is not suitable to choose very large impulsive distance in practical applications.
4. Conclusion
In the paper, impulsive synchronization of hyperchaotic Lü systems is studied. We use two methods to achieve
Figure 4. The boundaries of the stable region for Theorem 1.
Figure 5. The boundaries of the stable region for Theorem 2.
the sufficient conditions for synchronization and relevant analysis and comparison are presented. Mohammad et al. adopted the first method to study impulsive synchronization of hyperchaotic Chen systems [19] . The second method has not been reported before. Obviously it is more compatible than the first one. Numerical simulations show the effectiveness of the methods.
Acknowledgements
The work was supported by Doctor Specific Funds of Dalian University.
References
- Pecora, L. and Carroll, T. (1990) Synchronization in Chaotic Systems. Physical Review Letters, 64, 821-824. http://dx.doi.org/10.1103/PhysRevLett.64.821
- Carroll, T. and Pecora, L. (1991) Synchronizing Chaotic Circuits. IEEE Transactions on Circuits Systems, 38, 453-456. http://dx.doi.org/10.1109/31.75404
- Chen, G. and Dong, X. (1998) From Chaos to Order: Methodologies, Perspectives and Applications. World Scientific, Singapore.
- Wang, G.R., Yu, X.L. and Chen, S.G. (2001) Chaotic Control, Synchronization and Utilizing. National Defence Industry Press, Beijing.
- Wang, X.Y. (2003) Chaos in the Complex Nonlinearity System. Electronics Industry Press, Beijing.
- Chen, G.R. and Lü, J.H. (2003) Dynamical Analyses, Control and Synchronization of the Lorenz system family. Science Press, Beijing.
- Kemih, K., Bouraoui, H., Messadi, M. and Ghanes, M. (2013) Impulsive Control and Synchronization of a New 5D Hyperchaotic System. Acta Physica Polonica A, 123, 193-195. http://dx.doi.org/10.12693/APhysPolA.123.193
- Itoh, M., Yang, T. and Chua, L. (2001) Conditions for Impulsive Synchronization of Chaotic and Hyperchaotic Systems. International Journal of Bifurcation and Chaos, 11, 551-560. http://dx.doi.org/10.1142/S0218127401002262
- Chai, X., Gan, Z. and Shi, C. (2013) Impulsive Synchronization and Adaptive-Impulsive Synchronization of a Novel Financial Hyperchaotic System. Mathematical Problems in Engineering, 2013, 751616. http://dx.doi.org/10.1155/2013/751616
- Senouci, A. and Boukabou, A. (2014) Predictive Control and Synchronization of Chaotic and Hyperchaotic Systems Based on a T−S Fuzzy Model. Mathematics and Computers in Simulation, 105, 62-78. http://dx.doi.org/10.1016/j.matcom.2014.05.007
- Candido, R. and Eisencraft, M. (2014) Channel Equalization for Synchronization of Chaotic Maps. Digital Signal Processing, 33, 42-49. http://dx.doi.org/10.1016/j.dsp.2014.07.001
- Xiao, X., Zhou, L. and Zhang, Z. (2014) Synchronization of Chaotic Lur’e Systems with Quantized Sampled-Data Controller. Communications in Nonlinear Science and Numerical Simulation, 19, 2039-2047. http://dx.doi.org/10.1016/j.cnsns.2013.10.020
- Ren, Q. and Zhao, J. (2006) Impulsive Synchronization of Coupled Chaotic Systems via Adaptive-Feedback Approach. Physics Letters A, 355, 342-347. http://dx.doi.org/10.1016/j.physleta.2006.02.053
- Chen, Y. and Guo, J. (2014) Synchronization of a Class of Chaotic Systems Using Small Impulsive Signal. International Journal for Light and Electron Optics, 125, 6407-6412. http://dx.doi.org/10.1016/j.ijleo.2014.06.117
- Xi, H., Yu, S., Zhang, R. and Xu, L. (2014) Adaptive Impulsive Synchronization for a Class of Fractional-Order Chaotic and Hyperchaotic Systems. Optik―International Journal for Light and Electron Optics, 125, 2036-2040. http://dx.doi.org/10.1016/j.ijleo.2013.12.002
- Xu, Y., Wang, Y. and Zhao, J. (2014) A New Chaotic System without Linear Term and Its Impulsive Synchronization. Optik―International Journal for Light and Electron Optics, 125, 2526-2530. http://dx.doi.org/10.1016/j.ijleo.2013.10.123
- Chen, A., Lu, J., Lü, J. and Yu, S. (2006) Generating Hyperchaotic Lü Attractor via State Feedback Control. Physica A: Statistical Mechanics and its Applications, 364, 103-110. http://dx.doi.org/10.1016/j.physa.2005.09.039
- Lü, J., Lu, J. and Chen, S. (2002) Analysis and Applications of Chaotic Time Series. Wuhan University Press, Wuhan.
- Mohammad, H. and Mahsa, D. (2006) Impulsive Synchronization of Chen’s Hyperchaotic System. Physics Letters A, 356, 226-230. http://dx.doi.org/10.1016/j.physleta.2006.03.051













