International Journal of Modern Nonlinear Theory and Application
Vol.03 No.05(2014), Article ID:51248,7 pages
10.4236/ijmnta.2014.35021
Steady State Analysis of an Isolated Self-Excited Dual Three-Phase Induction Generator for Renewable Energy
Mohamed Arbi Khlifi, Badr M. Alshammari
College of Engineering, Hail University, Hail, KSA
Email: me.khlifi@uoh.edu.sa
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 September 2014; revised 18 October 2014; accepted 25 October 2014
ABSTRACT
In this paper modelling and analysis in autonomous mode of dual three-phase induction generator (DTPIG) with a new algorithm have been done. We develop the steady state model of a dual three- phase self-excited induction generator for stand-alone renewable generation dispensing with the segregating real and imaginary components of the complex impedance of the induction generator. The obtained admittance yields the adequate magnetizing reactance and the frequency. These two key parameters are then used to compute the self-excitation process requirements in terms of the prime mover speed, the capacitance and the load impedance on the one hand and to predict the generator steady state performance parameters on the other. Steady state performances and characteristics of different configurations are clearly examined and compared. The analytical results are found to be in good agreement with experimental results.
Keywords:
Dual stator windings, asynchronous generator, autonomous mode, steady state analysis, renewable electric energy generation

1. Introduction
The power rating of an ac drive system can be increased by using multi-phase drives system which has more than three phases in the stator of the machine. Multi-phase drives system possesses several advantages over conventional three-phase drives, such as reducing the amplitude and increasing the frequency of the torque pulsation, reducing the rotor harmonic currents, reducing the current per phase without increasing the voltage per phase, lowering the dc-link current harmonics, power segmentation and high reliability [1] -[5] . For this reason,
multi-phase induction machine drives are mainly related to the high-power and/or high-current applications such as in electric ship propulsion, in locomotive traction, in aerospace applications and in electric/hybrid vehicles [6] . Electric power systems have largely developed as three-phase systems, although high phase order (in excess of three) machine construction and power transmission have been considered for last several years. With the growth of increasingly sophisticated design methods and increased importance of economic, environmental and several other factors, the multi-phase systems are being considered as one of the potential alternatives to conventional three-phase systems. Authors in the literature deal with the dual stator machine with extended rotor common to both stators. In all the three cases, output is three-phase. Recently, two papers have reported on modeling and analysis of six-phase self-excited induction generator [7] [8] . However, so far the authors have been able to ascertain, practical applications of multi-phase (comprising of more than the conventional three phases) induction generator in hydropower scheme are still unreported. The major drawbacks in the use of self-exited DTPIG are the poor voltage and frequency regulations under prime mover speed and load perturbations [8] . The generated terminal voltage and the output frequency depend on the excitation capacitance, the dual three-phase induction generator parameters, the electrical passive load and the prime mover speed.
As a result, a multi-phase line with smaller dimensions can be used to transmit a larger amount of power covering entire range of transmission voltages [9] - [13] . Because of the potential benefits resulting from the use of a phase order higher than three in transmission, some interest has also grown in the area of DTPIG [14] . For machine drive applications, multi-phase system could potentially meet the demand for high power electric drive systems, which are both rugged and energy-efficient. High phase number drives possess several advantages over conventional three-phase drives such as: reducing the amplitude and increasing the frequency of torque pulsation, reducing the rotor harmonic currents, reducing the current per phase without increasing the voltage per phase, lowering the dc link current harmonics, higher reliability and increased power in the same frame. The high phase order drive is likely to remain limited to specialized applications where high reliability is demanded such as electric/hybrid vehicles, aerospace applications, ship propulsion, and high power application where a combination of several solid state devices form one leg of the drive [15] - [17] .
An imperative step in the steady state analysis of a self-exited DTPIG is to determine the magnetizing reactance 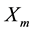 for given machine parameters, prime mover speed, and excitation capacitance and load impedance. In the usual practice, two basic approaches are used to determine the performance of self-exited DTPIG which are the loop impedance and the nodal admittance. They are very effective in evaluating the performances of this generator. Such methods are characterized by detailed algebraic derivations for the coefficients of the equations. However, these mathematical manipulations are tedious, time-consuming and prone to human errors. In addition, the coefficients established are valid only for this model. For example, if we change the type of load or include the core-loss resistance, all the mathematical treatments must be modified [18] [19] .
for given machine parameters, prime mover speed, and excitation capacitance and load impedance. In the usual practice, two basic approaches are used to determine the performance of self-exited DTPIG which are the loop impedance and the nodal admittance. They are very effective in evaluating the performances of this generator. Such methods are characterized by detailed algebraic derivations for the coefficients of the equations. However, these mathematical manipulations are tedious, time-consuming and prone to human errors. In addition, the coefficients established are valid only for this model. For example, if we change the type of load or include the core-loss resistance, all the mathematical treatments must be modified [18] [19] .
This paper, therefore, presents detailed investigations of self-excitation process with and without load condition. The machine performances are computed by solving the mathematical method of the developed steady state model via a numerical method. The computed results are compared with the experimental ones to validate the developed model. In this context we organized a paper as follows. Section 2 gives a detailed model of the self-exited dual three-phase induction generator. System studies, simulation and experimental results including steady state performance of the self-excited DTPIG, are presented in Section 3. Conclusions are drawn in Section 4.
2. Model of Self-Excited DTPAG
Often, steady state performances of SE-DTPAG are based on per phase equivalent circuit. This latter, is shown
in figure 1 where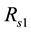 ,
, 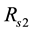 ,
,  ,
, 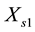 ,
, 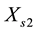 ,
, 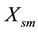 ,
, 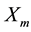 ,
, 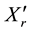 ,
, 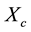 ,
, 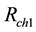 ,
, 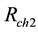 and
and 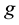 represent the stator
represent the stator
1 and 2 resistance, rotor resistance (referred to stator), stator 1 and 2 leakage reactance, mutual leakage reactance between the two stator, magnetizing reactance, rotor leakage reactance (referred to stator), excitation capacitor reactance, load resistance and the generator slip respectively. All parameters are considered constant except the magnetizing reactance and the generator slip which vary respectively according to the saturation characteristic and the prime mover speed. In this model the core loss component is neglected.
The other assumptions are the same. The steady state equations for a dual three-phase induction generator are given:
Figure 1. Equivalent circuit of dual stator self-excited induction generator.
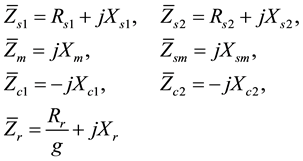 (1)
(1)
When the self-excited DTPIG is driven by dc machine in which the shaft speed is maintained constant. All parameters are fixed but both 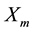 and
and 
At note “B” in Figure 2, the relation between




where:

Hence, equation (2) can be written as:

Under normal operating condition, the stator voltage 

This implies that both the real and imaginary parts of (6) would be separately zero.

Resolution of (7) leads to find the values of frequency 

Figure 2. Simple per phase equivalent circuit of DTPIG.
citation capacitor, speed, and electrical passive load.
At note “A” in Figure 2, the relation between



When the two sets of stator three-phase windings are identical, then we can write:

Using the method FZERO, we can predict the necessary parameters to evaluate the performance characteristics of the dual three-phase SEIG.
3. Simulation and Experimental Results
3.1. Brief description of the FZERO algorithm
To test the validity of the proposed method of analysis, and to investigate the performance characteristics of the DTPIG, the machine parameters of the equivalent circuit and simulation results have been considered. For this purpose, a dual three-phase induction machine, 230/380 V, 0.75 A, 4-pole, 50 Hz, Y-connected, was utilized. With load and blocked rotor tests were conducted to determine the parameters of the test machine for two schemes of operation. Computer tests were carried out with the star connected capacitors banks, connected to both three-phase sets of windings. A detailed study of steady state performance of the dual three-phase asynchronous generator indicates that for different operating conditions such as change in speed and different values star capacity.
The proposed method for computing the DTPIG performance is applied to a squirrel cage induction machine. In this proposed method, no further algebraic manipulations of the equations are needed. A numerical MATLAB function “FZERO” used in order to find root of this continuous function of one variable, which is the frequency. This function Find root of continuous function of one variable. This later, is a handle function, the “@.” operator constructs a function handle Equation (7), and assigns the handle to the output variable which is the frequency F. After the evaluation of the frequency, the magnetizing inductance can be deduced. This simple method reduces the time and effort needed to predict these necessary parameters to evaluate the performance characteristics of the SE-DSAG. With this method, the changing of the load type or including the core less resistance, do not oblige us to repeat the entire program. Alternatively, the values of star-capacitance at a given speed to generate a particular terminal voltage can be obtained experimentally by using a variable capacitor bank.
3.2. Dual Three-Phase SEIG Performance characteristics
A comparative study will be treated by using simulation and experiments tests. The dual stator SEIG supplied two individual three-phase resistive loads after switching-in a two star connected capacitor bank. To feed two- independent three-phase loads from dual three-phase generator, three-phase star connected load banks of variable resistance were connected two each three-phase winding set (figure 3).
A detailed study of steady state performance of the dual three-phase SEIG indicates that for different operating conditions such as change in speed and different values star-capacitance. Self-excitation under no-load con-
Figure 3. Scheme of self-excited dual three-phase induction ge- nerator.
dition and loading performance under a typical resistive load are elaborated. For simulation of no-load operation, 

The two star-capacitor SE-DTPIG needs a minimum value of capacitance to self-excites at no-load. The no-load terminal voltage can be computed for different value of star-capacitances using a computer algorithm for no-load conditions. Figure 4 shows, the behavior obtained from the experiment, of the output voltage as a function of rotor speed. These curves show two areas. The first, when the voltage increases very rapidly with the speed, the corresponding points are those obtained just after the self-excitation. In the second area, voltage varies linearly with the speed to a low coefficient. This area, where the characteristics are substantially parallel, corresponds to the stable part of the dual stator generator.
With the change in value of excitation capacitance, speed and terminal voltage both change. When the capacity believes, the generator operates more rapidly. Figure 5 and Figure 6 show the analytical variations of no- load terminal voltage and stator current with excitation capacitance connected to both the double three-phase stator sets at three different speeds.
As shown in Figure 7, the terminal voltage of the dual three-phase SEIG increases with increase in the value of the capacitance. However, the saturation of the magnetic circuit of the machine limits the indefinite rise of its terminal voltage. Moreover, the effect of speed on the stator voltage and corresponding capacitance may also be observed from this Figure 7. With increase in speed, the capacitance required decreases for a particular voltage, and vice versa. The value of the capacitance at which the machine loses excitation is called the critical capacitance. The value of the critical capacitance is inversely proportional to the square of the speed, therefore the critical square of the speed, therefore the critical capacitance decreases with increase in speed.
Experimental and computed result for variation of terminal voltage and frequency as function of load current are given in Figure 8 and Figure 9, respectively at three values of capacitor and at rated speed. From Figure 10, it is observed that there is a rise in load voltage with load when load current varies from 0 to 0.3 A, but it starts decreasing when load is further increased.
It is well known that for operation in self-excitation mode, the capacitive excitation is necessary to maintain the machine terminal voltage. If the speed is kept constant at
Figure 10 shows the variation of terminal voltage for stator1 versus load current for different values of prime mover speed. The excitation capacitance is fixed at a value of 
Figure 4. Output stator voltage versus speed for different values of capacity
Figure 5. Variation of terminal voltage with capacitance at no load
Figure 6. Variation of stator current with capacitance at no load
Figure 7. Stator current versus speed for different values of capacity
Figure 8. Terminal voltage for stator 1 with load current at three different capacitor
Figure 9. Output frequency versus load current at three different capacitor
Figure 10. Terminal voltage for stator 1 with load current
4. Conclusion
The paper discusses applicability of a dual three-phase capacitor excited asynchronous generator for supplying two individual three-phase loads and for supplying a single three-phase load, by presenting results of a simulation and an experimental study of the steady state behavior for various operating conditions. The proposed method can be easily extended to the analysis of the influence variation of excitation capacity and speed drive on the generator characteristics. Self-excitation and self-regulation under no-load condition and loading performance under a typical resistive load are elaborated. Hence, the dual three-phase SEIG offers an improved reliability, when compared to its three-phase counterpart. Further, it is also shown that the dual three-phase SEIG can be used to supply one or two independent three-phase loads. While the interaction between the two windings is inevitable, variation of the load at one winding changes operating conditions at the other winding. Very good correlation between simulation and experimental results can be observed.
Acknowledgements
This work was supported by the Arabian Saudi Ministry of Higher Education and Scientific Research and communication technology.
References
- Singh, G.K. (2008) Modeling and Experimental Analysis of a Self-Excited Six-Phase Induction Generator for Stand- Alone Renewable Energy Generation. Renewable Energy, 33, 1605-1621. http://dx.doi.org/10.1016/j.renene.2007.08.007
- Marwa, B.S., Mohamed Arbi, K., Mouldi, B. and Habib, R. (2013) The Process of Self Excitation in Dual Three-Phase Induction Generator. International Review of Electrical Engineering, 8, 1738-1744.
- Singh, G.K., Senthil, K.A. and Saini, R.P. (2011) Performance Analysis of a Simple Shunt and Series Compensated Six-Phase Self-Excited Induction Generator for Stand-Alone Renewable Energy Generation. Energy Conversion and Management, 52, 1688-1699. http://dx.doi.org/10.1016/j.enconman.2010.10.032
- Kheldoun, A., Refoufi, L. and Khodja, D.E. (2012) Analysis of the Self-Excited Induction Generator Steady State Performance Using a New Efficient Algorithm. Electric Power Systems Research, 86, 61-67. http://dx.doi.org/10.1016/j.epsr.2011.12.003
- Marwa, B.S., Mohamed Arbi, K., Mouldi, B. and Habib, R. (2014) Self Excitation in Dual Stator Winding Induction Generator for Renewable Energy Generation. The 5th International Renewable Energy Congress (IREC), Hammamet, 25-27 March 2014, 1024-1029.
- Haque, M.H. (2009) A Novel Method of Evaluating Performance Characteristics of a Self-Excited Induction Generator. IEEE Trans. Energy Conversion, 24, 358-365. http://dx.doi.org/10.1109/TEC.2009.2016124
- Parsa, L. (2005) On Advantages of Multi-Phase Machines. Industrial Electronics Society, IECON, 31st Annual Conference of IEEE, 6-10 November 2005, 1067-1071.
- Amimeur, H., Aouzellag, D., Abdessemed, R. and Ghedamsi, K. (2012) Sliding mode Control of a Dual-Stator Induction Generator for Wind Energy Conversion Systems. Electrical Power and Energy Systems, 42, 60-70. http://dx.doi.org/10.1016/j.ijepes.2012.03.024
- Singh, G.K., Senthil Kumar, A. and Saini, R.P. (2009) Selection of Capacitor for the Self-Excited Six-Phase Induction Generator. The 3rd IEEE International Conference on Power Systems, Kharagpur, 27-29 December 2009, 154-160.
- Levy, D. (1986) Analysis of a Double-Stator Induction Machine Used for Avariable-Speed/Constant-Frequency Small- Scale Hydro/Wind Electric Generator. Electric Power Systems Research, 11, 205-223. http://dx.doi.org/10.1016/0378-7796(86)90035-0
- Hadiouche, D., Razik, H. and Rezzoug, A. (2004) On the Modeling and Design of Dual-Stator Windings to Minimize Circulating Harmonic Currents for VSI Fed AC Machine. IEEE Transactions on Industry Applications, 40, 506-515. http://dx.doi.org/10.1109/TIA.2004.824511
- Yazdani, D., Khajehoddin, S.A., Bakhshai, A. and Joos, G. (2009) Full Utilization of the Inverter in Split-Phase Drives by Means of a Dual Three-Phase Space Vector Classification Algorithm. IEEE Transactions on Industry Electronics, 56, 120-129. http://dx.doi.org/10.1109/TIE.2008.927405
- Hallenius, K.-E., Vas, P. and Brown, J.E. (1991) The Analysis of a Saturated Self Excited Asynchronous Generator. IEEE Transactions on Energy Conversion, 6, 336-345. http://dx.doi.org/10.1109/60.79641
- Wang, L. and Su, J.Y. (1999) Dynamic Performances of an Isolated Self-Excited Induction Generator under Various Loading Conditions. IEEE Transactions on Energy Conversion, 14, 93-100. http://dx.doi.org/10.1109/60.749153
- Wang, L. and Lee, C.H. (2000) Long-Shunt and Short-Shunt Connections on Dynamic Performance of a SEIG Feeding an Induction Motor Load. IEEE Transactions on Energy Conversion, 15, 1-7. http://dx.doi.org/10.1109/60.849108
- Basic, D., Zhu, J.G. and Boardman, G. (2003) Transient Performance Study of a Brushless Doubly Fed Twin Stator Induction Generator. IEEE Transactions on Energy Conversion, 18, 400-408. http://dx.doi.org/10.1109/TEC.2003.815836
- Ojo, O. and Davidson, I.E. (2000) PWM-VSI Inverter-Assisted Stand-Alone Dual Stator Winding Induction Generator. IEEE Transactions on Energy Conversion, 36, 1604-1611.
- Singh, G.K., Yadav, K.B. and Saini, R.P. (2005) Modeling and Analysis of Multi-Phase (Six-Phase) Self Excitation Induction Generator. Proceedings of the 8th International Conference on Electrical Machines and Systems, Nanjing, 29-29 September 2005, 1922-1927.
- Selmi, M. and Rehaoulia, H. (2013) A Simple Method for the Steady State Performances of Self-Excited Induction Generators. Proceedings of IEEE International Conference on Electrical Engineering and Software Applications, Hammamet, 21-23 March 2013, 1-4.











