Open Journal of Fluid Dynamics
Vol.07 No.01(2017), Article ID:73012,14 pages
10.4236/ojfd.2017.71001
Thermal Radiation Effect on the MHD Turbulent Compressible Boundary Layer Flow with Adverse Pressure Gradient, Heat Transfer and Local Suction
Michalis Xenos
Department of Mathematics, Section of Applied Mathematics and Engineering Research, University of Ioannina, Ioannina, Greece

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 23, 2016; Accepted: December 24, 2016; Published: December 27, 2016
ABSTRACT
The combined effect of magnetic field, thermal radiation and local suction on the steady turbulent compressible boundary layer flow with adverse pressure gradient is numerically studied. The magnetic field is constant and applied transversely to the direction of the flow. The fluid is subjected to a localized suction and is considered as a radiative optically thin gray fluid. The Reynolds Averaged Boundary Layer (RABL) equations with appropriate boundary conditions are transformed using the compressible Falkner Skan transformation. The nonlinear and coupled system of partial differential equations (PDEs) is solved using the Keller box method. For the eddy-kinematic viscosity the Baldwin Lomax turbulent model and for the turbulent Prandtl number the extended Kays Crawford model are used. The numerical results show that the flow field can be controlled by the combined effect of the applied magnetic field, thermal radiation, and localized suction, moving the separation point, 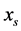 , downstream towards the plate’s end, and increasing total drag,
, downstream towards the plate’s end, and increasing total drag,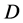 . The combined effect of thermal radiation and magnetic field has a cooling effect on the fluid at the wall vicinity. The combined effect has a greater influence in the case of high free-stream temperature.
. The combined effect of thermal radiation and magnetic field has a cooling effect on the fluid at the wall vicinity. The combined effect has a greater influence in the case of high free-stream temperature.
Keywords:
Computational Fluid Mechanics, Magnetic Field, Thermal Radiation, Local Suction, Turbulent Flow, Compressible Boundary Layer

1. Introduction
The idea of controlling the boundary layer flow of an electrically conducting fluid by electromagnetic forces dates back to the 60 s. Rossow was one of the first who studied the incompressible boundary layer flow over a flat plate in the presence of a uniform magnetic field applied normal to the plate [1] . Bleviss studied the magnetohydrodynamic (MHD) effects on hypersonic Couette flow under the influence of an externally imposed uniform magnetic field, normal to the wall [2] .
Recently, the influence of a magnetic field on the flow field has attracted new attention as a control technique for turbulent boundary layers. The magnetic field delays transition from laminar to turbulent flow and separation of the turbulent boundary layer. Transition delay results in a substantial skin friction reduction, since turbulent skin friction is orders of magnitude larger than the laminar one [3] . Delay of separation also reduces skin friction, because the separation phenomenon entails large energy losses [4] . In high Mach number MHD flows, the gas can become weakly ionized either by viscous heating at high temperatures or by artificially generated plasma at lower temperatures [5] . To obtain an acceptable value for the electrical conductivity of the fluid, seeding of an ion in the flow field has to take place [6] . Using the direct exhaust from a combustion process, the electrical conductivity is not zero and no seeding is required. Additionally, using short duration, high repetition rate, and high voltage pulses a cold supersonic gas can be ionized [7] .
The MHD laminar flow in the presence of radiation has been explored by several researchers. Israel-Cookey et al. studied the influence of viscous dissipation and radiation on the problem of unsteady MHD free-convection incompressible flow past an infinite vertical heated plate in an optically thin environment with time-dependent suction [8] . Siddheshwar and Mahabaleswar have studied the effects of radiation and heat source on the MHD viscoelastic flow [9] . Another study deals with the steady MHD flow of an incompressible second grade fluid past a semi-infinite fixed plate and provides approximate analytical solutions using the homotopy analysis method (HAM) [10] . The problem of a compressible turbulent boundary layer, under the influence of an applied magnetic field, is an important problem [11] [12] [13] [14] that becomes more interesting if the effect of an adverse pressure gradient is taken into consideration.
Thermal radiation has also significant effects on the flow field, especially at high temperatures with important engineering applications. Free convective laminar flow in the presence of radiation has been studied by Ali et al. [15] , Raptis and Toki [16] and Raptis and Perdikis [17] . Thermal radiation of an optically thin gray fluid has been studied in several incompressible flow configurations [18] [19] . Others have studied radiation effects on flow past a stretching plate with temperature dependent viscosity [20] . The interaction of thermal radiation on a vertical oscillating plate and the effect of radiation on a moving vertical plate have been studied by Muthucumaraswamy and Chandrakala [21] [22] .
Although many studies exist on the radiation effects on laminar incompressible flows, the study of MHD, compressible, and turbulent boundary layer flow under the influence of thermal radiation and adverse pressure gradient has received little attention. Anghaie and Chen, present a computational model for convective and radiative heat transfer in high temperature gas cooled and gaseous fuel nuclear reactors. Their model considers the turbulent and compressible flow under the effect of radiation in a large range of temperatures [23] . Their results are compared with experimentally based correlations, showing a good agreement. Duan et al. have studied the emission turbulence-radiation interaction in hypersonic boundary layer flows [24] [25] . In this study, when emission is coupled to the flow, the temperature is drastically decreased in the turbulent layer. Miroshnichenko et al. have performed a detailed numerical analysis of complex heat transfer (turbulent natural convection, conduction and surface thermal radiation) in a rectangular enclosure [26] [27] . In their analysis they concluded that the effect of thermal radiation leads to heat transfer enhancement. An essential cooling of the internal volume was found with an increase in the thermal conductivity ratio [27] . Kim and Baek studied the compressible turbulent flow over a backward facing step, showing that thermal behavior is influenced by radiation and the fluid is heated faster. Furthermore, the reattachment length of the recirculation area at the backward step is shrunk due to reduced adverse pressure gradient and the radiative heat flux was found to play a role in the recirculating zone [28] .
The subject of flow separation and stability analysis of compressible trailing edge flows has attracted enormous interest in aerodynamics. Turkyilmazoglu, in a theoretical study, has analyzed the structure of the lower branch neutral stability modes of three-dimensional small disturbances imposed on the compressible boundary layer flow due to a rotating-disk [29] . This study showed that the wave number and the orientation of the compressible lower branch modes are governed by an eigenrelation for the compressible stationary modes. The nonparallel influences tend to destabilize all the modes, though wall insulation and heating have a stabilizing effect on the modes in the vicinity of the stationary mode, unlike wall cooling. Additional numerical studies reveal that separation is enhanced as the relative thickness of the airfoil gets bigger and that the overall effect of compressibility is to reduce the extent of absolute instability at higher Mach numbers. The effect of wall heating is to enhance the absolute instability properties. On the other hand, cooling the wall greatly decreases the region of absolute instability regime for the studied Mach number range [30] [31] .
Prevention of flow separation is a challenging task, applicable to several engineering problems. Many passive and active techniques have been developed for the prevention of flow separation [32] . Fluid suction and injection have often been used as an active aerodynamic flow control technique to prevent turbulent flow separation. The combination of suction and injection is one of the most effective techniques for boundary layer control [33] . The response of the turbulent boundary layer under intense wall suction throughout the wall and under localized wall suction was studied by Oyewola et al. [34] and Kafoussias and Xenos [35] , respectively. The combined influence of localized injection and localized suction retains the boundary layer flow, reducing skin friction [36] . Heating or cooling of the wall is another mean of boundary layer control [37] .
The goal of this work is the numerical study of the combined effect of the magnetic field, thermal radiation and localized suction on the compressible turbulent boundary layer flow, over a permeable flat plate, in the presence of an adverse pressure gradient. The magnetic field is considered constant and applied to the whole length of the plate. In this study the localized suction, applied to the region of the separation point, is examined. The boundary layer flow is considered turbulent. The electrical conductivity of the fluid is varying with the temperature. The obtained results show that magnetic field, thermal radiation, and local suction influence the flow field and that the separation point is moved downstream to the end of the plate, rendering the above applications as possible flow control techniques.
2. Mathematical Formulation
We consider the steady two-dimensional compressible turbulent boundary layer flow over a smooth and permeable surface. The fluid is a gray, absorbing- emitting radiation, but a non-scattering, medium. It is considered an electrically and heat conducting perfect gas. The plate is an electrical insulator and a magnetic field of uniform strength is applied transversely to the direction of the flow. The magnetic field is assumed to be fixed with respect to the plate and the magnetic Reynolds number of the flow is small so that the induced magnetic field can be neglected [38] . Since no external electric field is applied and the effect of polarization of the ionized fluid is negligible [39] , the electric field is equal to zero. In a Cartesian coordinate system the flat surface is located at,  , where
, where 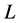 is the length of the plate and is parallel to the free- stream of the gas flowing with velocity,
is the length of the plate and is parallel to the free- stream of the gas flowing with velocity,  , in the positive
, in the positive 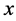 -direction (Figure 1). The equations governing the flow are the RABL equations which can be written for the MHD case under the effect of radiation, in Cartesian coordinates, as [35] [37] :
-direction (Figure 1). The equations governing the flow are the RABL equations which can be written for the MHD case under the effect of radiation, in Cartesian coordinates, as [35] [37] :
Continuity equation
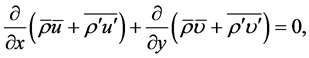 (1)
(1)
Figure 1. Schematic of the boundary layer flow above the flat plate under adverse pressure gradient.
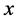 -momentum equation
-momentum equation
 (2)
(2)
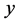 -momentum equation
-momentum equation
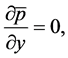 (3)
(3)
energy equation
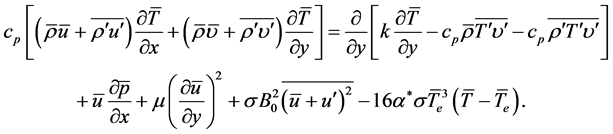 (4)
(4)
In the above equations we have replaced the instantaneous quantities , by the sum of their mean value,
, by the sum of their mean value, 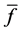 , and fluctuating parts,
, and fluctuating parts,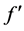 . The last term in Equation (2) is the Lorentz force, whereas the term before the last in (4) is the Joule-heating term. These terms are presented in the
. The last term in Equation (2) is the Lorentz force, whereas the term before the last in (4) is the Joule-heating term. These terms are presented in the  -momentum and energy equations when a magnetic field is applied in the flow field. The last term in (4) is the local radiant for the case of an optically thin gray fluid [20] , where
-momentum and energy equations when a magnetic field is applied in the flow field. The last term in (4) is the local radiant for the case of an optically thin gray fluid [20] , where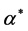 , is the absorption coefficient of the fluid and
, is the absorption coefficient of the fluid and


where the subscript, 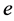




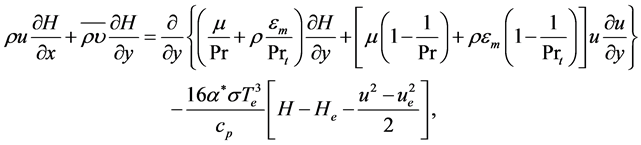
and the boundary conditions are,

where




where

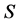



where







The problem under consideration is described by the system of Equations (11) and (12), subjected to the boundary conditions (13), where the coefficients entering into the equations are defined by the expressions (14). The coefficients



3. Baldwin Lomax Model and Turbulent Prandtl Number
In this study an algebraic turbulent model, Baldwin Lomax model (B-L), for the calculation of the eddy-viscosity and a mathematical model for the turbulent Prandtl number are employed. The B-L is an algebraic model that treats the turbulent boundary layer as a composite layer consisting of inner and outer regions. For the inner region the Prandtl-Van Driest formulation is used. For the outer region, Baldwin and Lomax introduced a formulation that replaces the Clauser formulation of the Cebeci Smith model, avoiding the necessity for finding the boundary layer edge [35] [41] .
The B-L turbulent model was developed for use in multi-dimensional Navier- Stokes codes and the results are in good agreement with the experimental data [42] [43] . Many researchers have opted the B-L algebraic model for its simplicity, although many modifications to its basic form have been employed [44] . Here, in order to study the mass transfer through the plate, we didn’t consider the “damping-length” parameter 
In this study a modification of the extended Kays and Crawford model is used [45] . The turbulent Prandtl number, 
4. Numerical Solution
In order to study the combined effect of an applied magnetic field, thermal radiation, and localized suction on the flow field a numerical scheme must be applied. The numerical scheme used to solve the parabolic system of PDEs, Equations (11)-(14), is a version of the Keller box method described in [35] [37] [47] [48] . The scheme is unconditionally stable, and second-order accuracy is achieved with nonuniform 



The free-stream values for the viscosity










In this study we apply a localized suction/injection velocity to a small slot over the plate near the separation point. To examine the influence of local suction we apply a Gaussian distribution [35] [46] [52] . To show the effect of the adverse pressure gradient on the flow field, we consider the linearly retarded flow, known as Howarth flow [35] [48] . For the numerical calculations, the length

In MHD boundary layer problems the parameter 
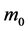

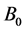
The developed numerical code was examined for grid independence [46] . A computational grid of 801 × 61 is sufficient to provide accurate numerical results by comparing the separation point, total drag and the maximum temperature for different grid realizations. For the numerical solution of the equations describing the problem a numerical program was developed in FORTRAN 90 [35] [46] [54] .
5. Results and Discussion
The most important parameters for engineering applications are the skin friction coefficient, 


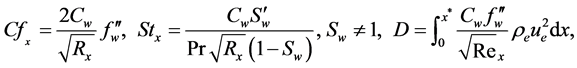
where 






Table 1 shows that the combined effect (magnetic field, thermal radiation, local suction) substantially influences the compressible boundary layer flow, by moving the separation point downstream, towards the end of the plate, and by increasing total drag for all studied Mach numbers. Thermal boundary layer is also influenced by the combined effect, with the maximum temperature being slightly increased compared to the control case (no MHD, no radiation, no local suction). The combination of the magnetic field, radiation, and local suction is more effective when the free-stream temperature is high due to the fact that both the magnetic field and the thermal radiation play a significant role in this case 
Figure 2 shows that at high free-stream temperature
Table 1. Numerical results for the cases of no MHD/radiation/suction and the combined effect of MHD, local suction, and thermal radiation, for different Mach numbers. The separation point, 



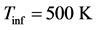
Figure 2. (a) Skin friction coefficient for two free-stream temperatures, 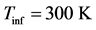

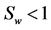
combined effect substantially influences the skin friction coefficient, 
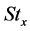
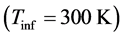
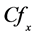

The developed numerical code was validated with other published computa- tional results and with experimentally based correlations, showing a good agreement for the case of radiation. More precisely, a comparison with previous computational studies and with experimentally based correlations for a specific problem setup is performed. In this problem, the wall is considered at a steady temperature of 1600 K and the temperature of the free stream is specified at 2000 K, which is a typical design temperature at the core inlet of a gaseous core reactor system [23] [55] . Additionally, the compressible turbulent results (con- trol case without radiation and magnetic field) have been validated and are in good qualitative agreement with previous studies [35] [37] .
It is also important to examine the dimensional quantities of the problem under consideration, such as the dimensional velocity and the dimensional temperature. The study of these two dimensional quantities provide a clear image of the shape of the boundary layer under adverse pressure gradient which is very different from the shape of the boundary layer with no pressure gradient. Figure 3, reveals the shape of the boundary layer under adverse pressure gradient for the case of cooling wall, 

Figure 3. (a) Velocity arrows in the boundary layer for the control case (above) and the MHD with radiation and local suction case (below). (b) Temperature contours in the boundary layer for the control and combined effect cases, for all cases Mach number, 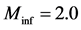

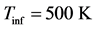
the maximum temperature increases by 12.2 K (1.5% increase), whereas the temperature decrease (cooling effect) in the boundary layer, close to the wall, is 124 K (17.5% decrease).
6. Conclusions
The combined effect of magnetic field, thermal radiation, and local suction on the steady turbulent compressible boundary layer flow with adverse pressure gradient is numerically studied. The magnetic field is constant and applied transversely to the direction of the flow. The fluid is subjected to a localized suction and is considered as a radiative optically thin gray fluid. The RABL equations with appropriate boundary conditions are transformed using the compressible Falkner Skan transformation. The nonlinear and coupled system of PDEs is solved using the Keller box method. For the eddy-kinematic viscosity, the B-L turbulent model is used. For the turbulent Prandtl number, the extended Kays Crawford model is used.
The numerical results show that the combined effect of the magnetic field, thermal radiation, and local suction substantially influences the turbulent boun- dary layer, by shifting the separation point downstream to the end of the plate, and increasing total drag. The magnetic field has a greater influence on the flow field in the case of high free-stream temperature. Additionally, the influence of the magnetic field, thermal radiation, and local suction on the thermal boundary layer is significant. The combination of these boundary layer control techniques has a cooling effect on the fluid at the wall vicinity.
Acknowledgements
The author thanks the reviewer for the valuable comments and suggestions.
Cite this paper
Xenos, M. (2017) Thermal Radiation Effect on the MHD Turbulent Compressible Boundary Layer Flow with Adverse Pressure Gradient, Heat Transfer and Local Suction. Open Journal of Fluid Dynamics, 7, 1-14. http://dx.doi.org/10.4236/ojfd.2017.71001
References
- 1. Rossow, V.J. (1957) On Flow of Electrically Conducting Fluids over a Flat Plate in the Presence of a Transverse Magnetic Field, Report 1358.
- 2. Bleviss, Z.O. (1958) Magnetogasdynamics of Hypersonic Couette Flow. Journal of Aero/Space Science, 25, 601-615. https://doi.org/10.2514/8.7812
- 3. Weier, T., Fey, U., Gerbeth, G., Mutschke, G. and Avilov, V. (2000) Boundary Layer Control by Means of Electromagnetic Forces. ERCOFTAC Bulletin, 44, 36-40.
- 4. Schlichting, H. and Gersten, K. (2000) Boundary-Layer Theory. 8th Edition, Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-642-85829-1
- 5. Cheng, F., Zhong, X., Gogineni, S. and Kimmel, R.L. (2003) Magnetic-Field Effects on Second-Mode Instability of a Weakly Ionized Mach 4.5 Boundary Layer. Physics of Fluids, 15, 2020-2040. https://doi.org/10.1063/1.1577565
- 6. Resler, E.L. and Sears, W.R. (1958) The Prospects for Magneto-Aerodynamics. Journal Aeronautical Science, 25, 235-258.
- 7. Murray, R.C., Zaidi, S.H., Carraro, M.R., Vasilyak, L., Macheret, S.O., Shneider, M.N. and Miles, R.B. (2003) Investigation of a Mach 3 Cold Air MHD Channel. 34th AIAA Plasmadynamics and Laser Conference, AIAA 2003-4282. https://doi.org/10.2514/6.2003-4282
- 8. Israel-Cookey, C., Ogulub, A. and Omubo-Peppleb, V.B. (2003) Influence of Viscous Dissipation and Radiation on Unsteady MHD Free-Convection Flow past an Infinite Heated Vertical Plate in a Porous Medium with Time-Dependent Suction. International Journal of Heat and Mass Transfer, 46, 2305-2311. https://doi.org/10.1016/S0017-9310(02)00544-6
- 9. Siddheshwar, P.G. and Mahabaleswar, U.S. (2005) Effects of Radiation and Heat Source on MHD Flow of a Viscoelastic Liquid and Heat Transfer over a Stretching Sheet. International Journal of Non-Linear Mechanics, 40, 807-820.
https://doi.org/10.1016/j.ijnonlinmec.2004.04.006 - 10. Hayat, T., Abbas, Z., Sajid, M. and Asghar, S. (2007) The Influence of Thermal Radiation on MHD Flow of a Second Grade Fluid. International Journal of Heat and Mass Transfer, 50, 931-941. https://doi.org/10.1016/j.ijheatmasstransfer.2006.08.014
- 11. Dahlburg, R.B. and Picone, J.M. (1990) Pseudospectral Simulation of Compressible Magnetohydrodynamic Turbulence. Computer Methods in Applied Mechanics and Engineering, 80, 409-416. https://doi.org/10.1016/0045-7825(90)90045-n
- 12. Satake, S.-I., Kunugi, T. and Smolentsev, S. (2002) Advances in Direct Numerical Simulation for MHD Modeling of Free Surface Flows. Fusion Engineering and Design, 61-62, 95-102. https://doi.org/10.1016/S0920-3796(02)00157-6
- 13. Brandenburg, A. and Dobler, W. (2002) Hydromagnetic Turbulence in Computer Simulations. Computer Physics Communications, 147, 471-475.
https://doi.org/10.1016/S0010-4655(02)00334-X - 14. Passot, T. and Vázquez-Semadeni, E. (2003) The Correlation between Magnetic Pressure and Density in Compressible MHD Turbulence. Astronomy & Astrophysics, 398, 845-855.
https://doi.org/10.1051/0004-6361:20021665 - 15. Ali, M.M., Chen, T.S. and Armaly, B.F. (1984) Natural Convection-Radiation Interaction in Boundary-Layer Flow over Horizontal Surfaces. AIAA Journal, 22, 1797-1803.
https://doi.org/10.2514/3.8854 - 16. Raptis, A. and Toki, C.J. (2009) Thermal Radiation in the Presence of Free Convective Flow past a Moving Vertical Porous Plate: An Analytical Solution. International Journal of Applied Mechanics and Engineering, 14, 1115-1126.
- 17. Raptis, A. and Perdikis, C. (1999) Radiation and Free Convection Flow past a Moving Plate. Applied Mechanics and Engineering, 4, 817-821.
- 18. Raptis, A. and Perdikis, C. (2003) Thermal Radiation of an Optically Thin Gray Gas. International Journal of Applied Mechanics and Engineering, 8, 131-134.
- 19. Seddeek, M.A. and Abdelmeguid, M.S. (2006) Effects of Radiation and Thermal Diffusivity on Heat Transfer over a Stretching Surface with Variable Heat Flux. Physics Letters A, 348, 172-179. https://doi.org/10.1016/j.physleta.2005.01.101
- 20. Xenos, M. (2013) Radiation Effects on Flow past a Stretching Plate with Temperature Dependent Viscosity. Applied Mathematics, 4, 1-5. https://doi.org/10.4236/am.2013.49A001
- 21. Muthucumaraswamy, R. (2006) The Interaction of Thermal Radiation on Vertical Oscillating Plate with Variable Temperature and Mass Diffusion. Theoretical and Applied Mechanics, 33, 107-121. https://doi.org/10.2298/TAM0602107M
- 22. Muthucumaraswamy, R. and Chandraqkala, P. (2005) Effects of Thermal Radiation on Moving Vertical Plate in the Presence of an Optically Thin Gray Gas. Forschung im Ingenieurwesen, 69, 205-208. https://doi.org/10.1007/s10010-005-0003-3
- 23. Anghaie, S. and Chen, G. (1998) Application of Computational Fluid Dynamics for Thermal Analysis of High Temperature Gas Cooled and Gaseous Core Reactors. Nuclear Science and Engineering, 130, 361-373.
- 24. Duan, L., Martin, M.P., Sohn, I., Levin, D.A. and Modest, M.F. (2011) Study of Emission Turbulence-Radiation Interaction in Hypersonic Boundary Layers. AIAA Journal, 49, 340-348.
https://doi.org/10.2514/1.J050508 - 25. Duan, L., Martin, M.P., Feldick, A.M., Modest, M.F. and Levin, D.A. (2012) Study of Turbulence-Radiation Interaction in Hypersonic Turbulent Boundary Layers. AIAA Journal, 50, 447-453. https://doi.org/10.2514/1.J051247
- 26. Miroshnichenko, I.V. and Sheremet, M.A. (2015) Numerical Simulation of Turbulent Natural Convection Combined with Surface Thermal Radiation in a Square Cavity. International Journal of Numerical Methods for Heat & Fluid Flow, 25, 1600-1618.
https://doi.org/10.1108/HFF-09-2014-0289 - 27. Miroshnichenko, I.V., Sheremet, M.A. and Mohamad, A.A. (2016) Numerical Simulation of a Conjugate Turbulent Natural Convection Combined with Surface Thermal Radiation in an Enclosure with a Heat Source. International Journal of Thermal Sciences, 109, 172-181.
https://doi.org/10.1016/j.ijthermalsci.2016.06.008 - 28. Kim, S.S. and Baek, S.W. (1996) Radiation Affected Compressible Turbulent Flow over a Backward Facing Step. International Journal of Heat and Mass Transfer, 39, 3325-3332.
https://doi.org/10.1016/0017-9310(96)00046-4 - 29. Turkyilmazoglu, M. (2005) Lower Branch Modes of the Compressible Boundary Layer Flow Due to a Rotating-Disk. Studies in Applied Mathematics, 114, 17-43.
https://doi.org/10.1111/j.0022-2526.2005.01535.x - 30. Turkyilmazoglu, M. (2003) Instability of the Flow in the Vicinity of Trailing Edge of a Class of Thin Aerofoils. Computers and Fluids, 32, 353-371.
https://doi.org/10.1016/S0045-7930(01)00088-3 - 31. Turkyilmazoglu, M. and Cole, J.W. and Gajjar, J.S.B. (2000) Absolute and Convective Instabilities in the Compressible Boundary Layer on a Rotating Disk. Theoretical and Computational Fluid Dynamics, 14, 21-37. https://doi.org/10.1007/s001620050123
- 32. Narayanan, S. and Banaszuk, A. (2003) Experimental Study of a Novel Active Separation Control Approach. AIAA Paper 2003-60.
- 33. Achala, N.L. and Sathyanarayana, S.B. (2015) Approximate Analytical Solution of Compressible Boundary Layer Flow with an Adverse Pressure Gradient by Homotopy Analysis Method. Theoretical Mathematics & Applications, 5, 15-31.
- 34. Oyewola, O., Djenidi, L. and Antonia, R.A. (2003) Combined Influence of the Reynolds Number and Localised Wall Suction on a Turbulent Boundary Layer. Experiments in Fluids, 35, 199-206.
https://doi.org/10.1007/s00348-003-0658-1 - 35. Kafoussias, N.G. and Xenos, M.A. (2000) Numerical Investigation of Two-Dimen-sional Turbulent Boundary-Layer Compressible Flow with Adverse Pressure Gradient and Heat and Mass Transfer. Acta Mechanica, 141, 201-223. https://doi.org/10.1007/BF01268678
- 36. Roy, S. (2000) Nonuniform Slot Injection (Suction) into a Compressible Flow. Acta Mechanica, 139, 43-56. https://doi.org/10.1007/BF01170181
- 37. Cebeci, T. and Bradshaw, P. (1984) Physical and Computational Aspects of Convective Heat Transfer. Springer, New York. https://doi.org/10.1007/978-3-662-02411-9
- 38. Cramer, K.R. and Pai, S.I. (1973) Magnetofluid Dynamics for Engineers and Applied Physicists. McGraw-Hill, New York.
- 39. Pop, I., Kumari, M. and Nath, G. (1994) Conjugate MHD Flow past a Flat Plate. Acta Mechanica, 106, 215-220. https://doi.org/10.1007/BF01213563
- 40. Sutton, G.W. and Sherman, A. (1965) Engineering Magnetohydrodynamics. McGraw-Hill, New York.
- 41. Baldwin, B. and Lomax, H. (1978) Thin-Layer Approximation and Algebraic Model for Separated Turbulent Flows. AIAA Paper 78-205.
- 42. Steger, J.L. (1977) Impicit Finite Difference Simulation of Flow about Arbitrary Geometries with Application to Airfoils. AIAA 12th Thermophysics. Conference, AIAA Paper 77-665, Albuqurque, 27-29 June 1977.
- 43. Pulliam, T.H. and Steger, J.L. (1980) Implicit Finite-Difference Simulations of Three-Dimensional Compressible Flow. AIAA Journal, 18, 159-167. https://doi.org/10.2514/3.50745
- 44. Wolfe Candler, G.E. (1995) Comparison of Baldwin-Lomax Turbulence Models for Two-Dimensional Open Cavity Computations. AIAA Journal, 34, 629-631.
https://doi.org/10.2514/3.60019 - 45. Weigand, B., Ferguson, J.R. and Crawford, M.E. (1997) An Extended Kays and Crawford Turbulent Prandtl Number Model. International Journal of Heat Mass Transfer, 40, 4191-4196.
https://doi.org/10.1016/S0017-9310(97)00084-7 - 46. Xenos, M., Dimas, S. and Kafoussias, N. (2005) MHD Compressible Turbulent Boundary Layer Flow with Adverse Pressure Gradient. Acta Mechanica, 177, 171-190.
https://doi.org/10.1007/s00707-005-0221-7 - 47. Cebeci, T. and Smith, A.M.O. (1974) Analysis of Turbulent Boundary Layers. Academic Press, New York.
- 48. Kafoussias, N., Karabis, A. and Xenos, M. (1999) Numerical Study of Two Dimensional Laminar Boundary Layer Compressible Flow with Pressure Gradient and Heat and Mass Transfer. International Journal of Engineering Science, 37, 1795-1812.
https://doi.org/10.1016/S0020-7225(99)00002-6 - 49. Keller, H.B. (1970) A New Difference Scheme for Parabolic Problems. In: Hubbard, B., Ed., Numerical Solutions of Partial Differential Equations, Vol. 2, Academic Press, New York, 327-350.
- 50. Tannehill, J.C. anderson, D.A. and Pletcher, R.H. (1997) Computational Fluid Mechanics and Heat Transfer. 2nd Edition, Taylor & Francis, Milton Park.
- 51. Cecilio, W.A., Cordeiro, C.J., Mill, I.S., Santiago, C.D., Zanardini, R.A.D. and Yuan, J.Y. (2002) A Note on Polynomial Interpolation. International Journal of Computer Mathematics, 79, 465-471. https://doi.org/10.1080/00207160210937
- 52. Chung, Y.M., Sung, H.J. and Boiko, A.V. (1997) Spatial Simulation of the Instability of Channel Flow with Local Suction/Blowing. Physics of Fluids, 9, 3258-3266.
https://doi.org/10.1063/1.869423 - 53. Bush, W.B. (1960) Compressible Flat-Plate Boundary-Layer Flow with an Applied Magnetic Field. Journal of the Aero/Space Sciences, 27, 49-58. https://doi.org/10.2514/8.8373
- 54. Xenos, M., Kafoussias, N. and Karahalios, G. (2001) Magnetohydrodynamic Compressible Laminar Boundary Layer Adiabatic Flow with Adverse Pressure Gradient and Continuous or Localized Mass Transfer. Canadian Journal of Physics, 79, 1247-1263.
https://doi.org/10.1139/p01-067 - 55. Xenos, M. and Pop, I. (2017) Radiation Effect on the Turbulent Compressible Boundary Layer Flow with Adverse Pressure Gradient. Applied Mathematics and Computation, 299, 153-164.
http://dx.doi.org/10.1016/j.amc.2016.11.024





